基于 MEMS⁃INS/GNSS 组合导航抗差自适应Kalman滤波算法

周 彬，赵万良，荣义杰，胡小毛，马吉雨

（1.上海航天控制技术研究所，上海201109；2.上海惯性工程技术研究中心，上海201109）

0 引言

标准的Kalman滤波器在 MEMS-INS/GNSS组合导航领域已得到广泛的应用，标准Kalman滤波解为最小方差滤波解，但它需要有一定的条件：适合的估计方法、可靠的观测信息以及准确的动态模型。然而，在实际应用中，系统的动态模型是复杂多变的，其中包括超高速运动、振动环境、变加速运动、超机动运动等运动状态。针对这些复杂运动状态，构建精确的系统动态模型是非常困难的，这需要对载体的运动特性有充分准确的掌握。另外，GNSS接收机在复杂运动环境下易受干扰，导致卫星信号的观测信息误差瞬时增大。如果不对这些异常的信息做特别的处理，那么当前系统的动态模型参数的估计值和观测信息是不准确的，经过Kalman滤波之后则会导致滤波结果发散。因此，如何利用当前观测信息和状态估值更新先验信息和补偿运动方程误差，已成为当前组合导航领域尤其是动态导航技术研究领域的热点及难点之一。

近年来，为了进一步减弱动态模型和观测信息带来的误差的影响，先后发展了自适应滤波、抗差滤波、Sage自适应滤波等。本文在Kalman滤波的基础上，设计了抗差自适应Kalman滤波对组合导航系统进行研究。根据实验结果可以得到：利用抗差自适应kalman滤波能够有效地抑制误差发散，提供更加精确的导航结果。而且相比于标准Kalman滤波，基于抗差自适应滤波的组合导航系统的误差波动幅度降低了很多，能够更好地控制观测信息误差以及动力学模型异常所带来的影响，在组合导航领域上具有很好的研究意义。

1 抗差自适应Kalman滤波器的设计

首先对标准的 Kalman滤波进行分析，设Kalman滤波的状态方程为：

式（1）中，Xk为tk时刻状态向量，Xk－1为tk－1时刻的m维状态向量，Wk为Gauss白噪声过程误差向量，Φk，k－1为tk－1时刻m×m阶状态转移矩阵。

Kalman滤波的观测方程为：

式（2）中，Vk为n×m阶的观测噪声向量，Hk为n×m阶的观测矩阵。

1）预测的状态向量：

2）预测的状态向量协方差矩阵：

3）增益矩阵：

4）新一时刻的状态估计值：

5）新一时刻的状态估计值的协方差矩阵：

从式（3）～式（7）可以得到，Kalman 滤波是采用递推的算法对状态空间进行一系列的动态估计，即根据前一时刻参数的估计值和新一时刻的观测数据进行状态参数的更新。当系统的动态模型参数的估计值和观测信息是不准确的，滤波器得到的估计误差的方差可能趋于无穷大，估计值具有有偏性，即发生滤波发散的现象。

Kalman滤波的极值条件为：

式（8）中，Pk为Lk的权矩阵，为的权矩阵，Lk和互为不相关，为系统的状态预测向量。根据式（8）可以推导出标准Kalman滤波的解为：

当系统的观测数据不准确时，则将Kalman滤波的极值条件变换成抗差滤波的极值条件。

式（10）对观测向量采用了抗差估计的原则，而对状态参数的先验值采用最小二乘的原则，故可称为M-LS滤波原则，可以得到抗差估计值为：

可以看出，式（11）的Kalman滤波解与式（10）的抗差估计值的形式是基本一致的，只是用观测向量Zk的抗差协方差矩阵替换掉原先的协方差矩阵Σk。 当预测的动态模型与实际运动状态有偏差或者是动态模型发生异常时，则采用自适应滤波方法，该滤波原则为：

式（12）中，αk为自适应因子（0≤αk≤1）。αk的取值是根据动力学模型误差大小决定的，当动力学模型的误差小于某个设定的阈值时，则αk＝1；当动力学模型的误差大于某个设定的阈值时，则αk＜1。当αk的值确定之后，得到自适应滤波的解为：

抗差估计主要是对观测信息中的随机变量进行判断，当系统的观测信息存在较大的偏差或者发生异常现象时，通过降低异常观测信息的权重来减小异常观测信息对滤波结果的影响。而自适应滤波则是根据观测量信息是否正确来判断系统的动力学模型信息是否发生异常，若观测量信息发生异常情况，则判定动力学模型信息有误，因此观测量信息的可靠程度直接影响了整个系统滤波的效果。当动力学模型和观测量信息同时发生异常时，为了降低两种异常情况对状态参数估计值的影响，根据抗差估计原理以及自适应估计原理可实现抗差自适应滤波，该滤波构造极值原则如下：

式（14）对动态系统的状态预测信息采用了自适应估计原则，而对观测向量信息采用了抗差估计原则，对状态参量估值求极值后，可得：

根据式（15），可以得到观测残差和状态预测残差为：

将式（16）和式（17）代入式（15），可以计算出抗差自适应滤波解为：

至此，就可以得到抗差自适应Kalman滤波的解。抗差自适应滤波解的流程如图1所示，抗差自适应滤波是通过改变自适应因子以及等价权矩阵的值，来降低动观测向量信息异常误差与动力学模型异常误差对滤波器的影响。当运动载体的实际运动状态与设定的动力学模型有较大的偏差时，则通过减小自适应因子αk的值来抑制系统状态模型预测信息异常对状态参数估计值的影响。当观测向量信息存在较大的误差时，即观测向量发生异常，则减小对应的观测噪声的等价权矩阵的元素，从而降低观测向量信息异常对状态参量估计值的影响。当动力学模型与观测向量信息都正常时，即αk＝1，，整个动态系统则是正常利用动力学模型以及观测向量信息进行最优滤波估计，此时的抗差自适应滤波就是标准Kalman滤波。

准确地观测噪声等价权矩阵和自适应因子能够有效地减小因异常信息而产生的误差，因此，如何构造正确的等价权矩阵以及自适应因子是整个抗差自适应滤波理论的关键。对观测噪声等价权矩阵进行求解，得到状态向量的抗差估计值为：

式（19）中，为观测矩阵。 由式（19）可以推导得到残差向量为：

通过采用Huber的两段函数法，可以求得基于残差向量的观测等价权矩阵元素：

式（21）中，σVki为残差分量Vki的均方差，为标准化残差，qi为观测向量Zk的等价权矩阵的第i个对角线元素。

接下来是对自适应因子进行构造，常用的构造方法有两种：两段函数法和三段函数法。

（1）两段函数法

两段函数模型是非归零函数的一种，若判别统计量增大，自适应因子的值则会随之减小，反之亦然，但自适应因子的值永不为0。两段函数模型所表示的自适应因子为：

式（22）中，c为常量，一般在1.0～2.5之间取值，其最优值为1。

式（23）中，自适应因子的取值为0＜αk≤1，Δk为状态不符值统计量，当 Δ越大，αk越小，动力学模型的权重也就越小。

（2）三段函数法

与二段函数法相同，三段函数表示的自适应因子为：

式（24）中，c0和c1分别为两个常量，它们的取值为c0＝1.0～1.5，c1＝3.0～4.5，自适应因子的取值为0≤αk≤1。

由上述方法得到自适应因子后，就可以计算出对应的滤波解：递推解和加权平均解。

递推解满足：

加权平均解为：

其中，递推解中的自适应因子不能为0，因此不适用于三段函数法。另外，状态参量的预测值与当前历元观测得到的状态参量抗差估计值之差所组成的函数决定自适应因子的取值，该函数的值能反映状态参量预测值的偏离程度，该值越大，则表明系统的实际观测值与状态预估值偏差越大。

式（27）中，为当前历元的状态预测向量，，r为状态参数抗差估计值。

当观测向量无偏时，即E（Zk）＝HkXk，滤波解，a的数学期望为：

若状态预测向量也无偏，即E（），则：

根据式（29），当状态预测量X～k和观测量Zk均无异常误差时，那么自适应滤波解也满足无偏性。从理论研究可以得到，抗差自适应滤波通过引入自适应因子和等价权矩阵能够有效地降低状态信息异常和观测向量信息异常带来的影响。

2 跑车试验与性能分析

为了进一步验证本文设计的相关算法以及分析组合导航系统的性能情况，本文进行了MEMSINS/GNSS组合导航系统的跑车试验，跑车运动的三维动态轨迹如图2所示。在跑车试验中，组合导航系统安装固定在汽车内，MEMS-INS和GNSS同时采集双方的数据，数据保存后并在Matlab中进行时间对准以及滤波分析。

整个跑车试验过程总共有8颗可见星（2、7、9、10、15、20、25、30号卫星），其中10号卫星的高度角最高作为基准卫星，本文选取某一段GNSS信号较为广阔的一组数据进行分析。图3～图5为MEMS-INS/GNSS组合导航相较于基准导航系统的姿态角误差图。

对上述数据进行相应的统计分析，得到在不同滤波算法下的组合导航系统的姿态角误差均值，如表1所示。

本文选取了一组时间较长的位置和速度信息数据，经过解算得到组合导航系统的位置、速度误差如图6所示。

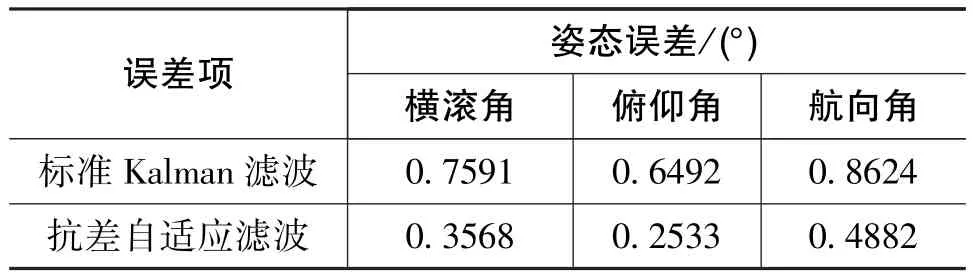
表1 不同滤波算法下的系统姿态角误差Table 1 System attitude error under different filtering algorithms

经过数理统计得到位置、速度误差，如表2、表3所示。

从两种滤波的误差结果可以得到，利用抗差自适应Kalman滤波能够有效地抑制误差发散，提供更加精确的导航结果，而且相比于标准Kalman滤波，基于抗差自适应滤波的组合导航系统的误差波动幅度降低了很多，能够更好地控制观测信息误差以及动力学模型异常所带来的影响。

表2 组合导航系统的位置误差Table 2 Position error of integrated navigation system

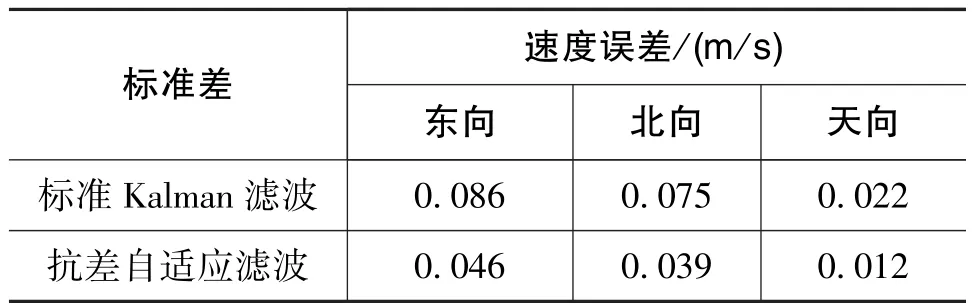
表3 组合导航系统的速度误差Table 3 Velocity error of integrated navigation system

3 结论

本文针对高动态环境下载体动态复杂多变特性带来的动力学模型难以精确构建问题，以及卫星跟踪环路信号易受扰动导致的观测信息出现异常粗差问题，设计了一种基于MEMS-INS/GNSS组合导航系统抗差自适应Kalman滤波算法，并研究了优化自适应因子的求解方法。最后，通过跑车实验验证了抗差自适应Kalman滤波算法的抗异常粗差能力以及抗干扰能力。