基于分数阶和非局部全变差模型的图像去模糊
2018-07-19向雨晴杨晓梅
向雨晴,杨晓梅
(四川大学 电气信息学院,四川 成都 610065)
0 引 言
作为一种基础的图像复原技术,图像去模糊广泛应用于各个图像领域。图像模糊过程在数学上可看成模糊核和原始清晰图像卷积运算后加噪声的操作,可表示为
f=h*x+n
(1)
式中:f表示退化图像,x表示原始清晰图像,h表示模糊核,*表示卷积运算,n表示附加噪声。本文讨论的是已知f、h求x的非盲去模糊逆问题,基于正则化的全变差(TV)方法经常用于求解此类问题。L.Rudin等提出基于TV的图像ROF去噪模型,其强大的边缘保护能力使之应用到去模糊及图像重建等领域[1,2],但该模型会使图像产生阶梯效应,对纹理细节的恢复也并不具有优势。
为了更好地利用图像本身的先验信息,文献[3]提出基于非局部全变差(NLTV)正则化的图像重建模型,更好地恢复了图像纹理细节。为减少阶梯效应和避免高阶全变差(HOTV)模型的边缘过平滑的缺点,基于TV的衍生形式——分数阶全变差(FOTV)模型得到提出和应用[4,5]。考虑到综合利用NLTV和FOTV的优势,本文运用全局梯度提取法(GGES)[6,7]把图像分成平滑和细节两部分,分别对其进行FOTV和NLTV正则化约束,提出了一种结合这两种TV正则化方法的非盲去模糊模型,它一方面减少了阶梯效应和边缘过平滑的现象,另一方面能很好地保留图像的纹理细节,比单独运用FOTV或NLTV的模型更具优势,且对不同级别的噪声具有一定的鲁棒性。
1 FOTV和NLTV的非盲去模糊模型
1.1 基于FOTV的非盲去模糊模型
分数阶有界变差是传统的有界变差空间的推广和延伸,其在形式上和传统的TV模型并无差异,只是有界变差空间建立在分数阶梯度模值的基础上,其首先被用于图像去噪和超分辨率重建方面。基于FOTV的图像非盲去模糊重建模型为
(2)
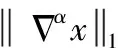
(3)
关于α取值对应的分数阶微分算子的幅频特性曲线如图1所示。
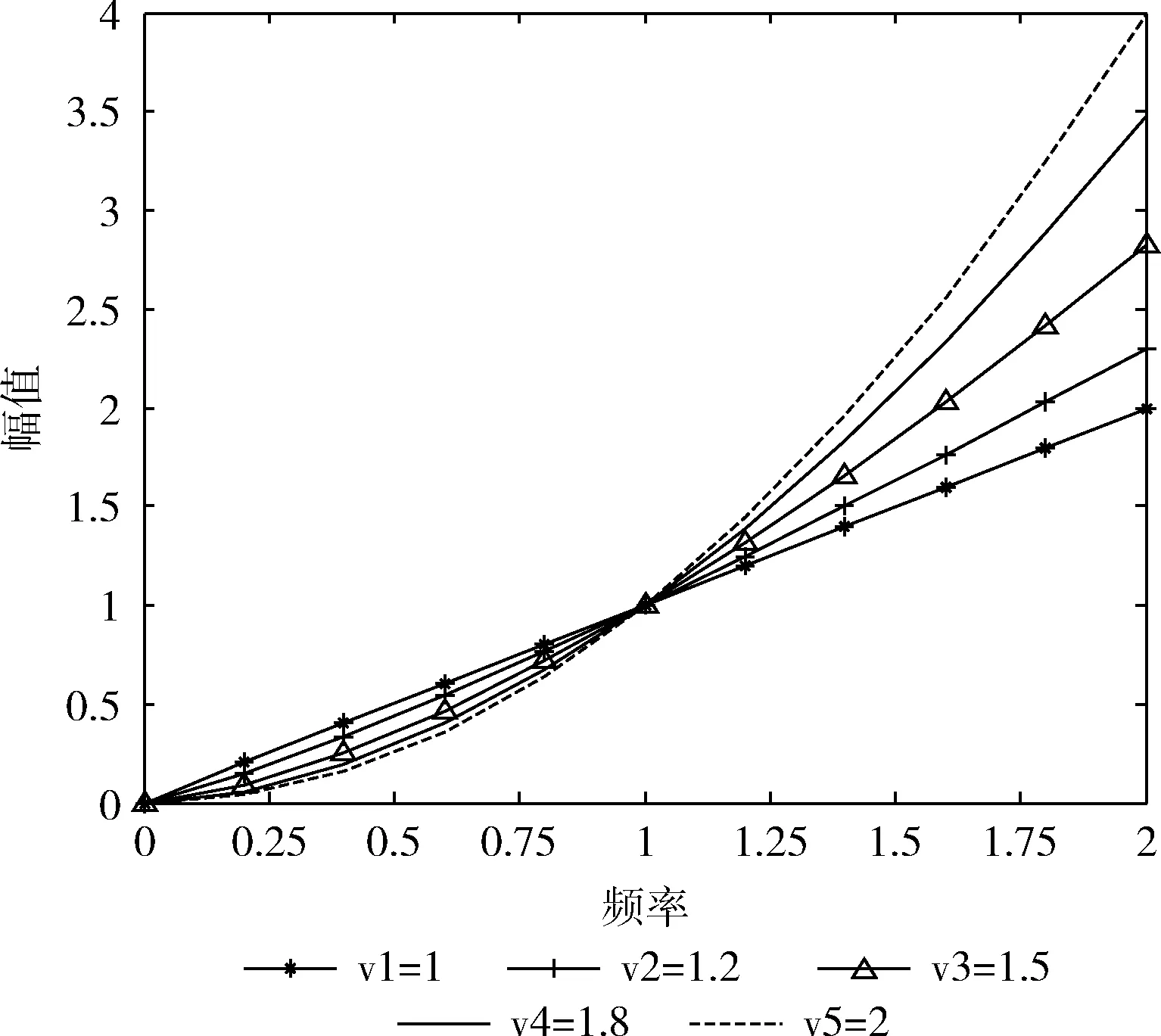
图1 分数阶微分幅频特性曲线
由图1可知,不同阶次(α>1)的分数阶微分算子对信号均有提高的作用,且频率越高,提高作用呈非线性增长;对于高频信号,分数阶阶次越大提高效果越明显,对于低频信号,阶次越小提高效果越佳。当阶次等于1,此时的FOTV模型即为传统的TV形式;当阶次取大于2的整数,则演变成HOTV的形式。传统的TV正则化模型去模糊时通常伴随阶梯效应,而HOTV可以消除阶梯效应但又会产生边缘过平滑这一负效应[8];当阶次取稍大于1的分数,FOTV正则化模型可以消除阶梯效应的同时避免边缘过平滑。基于此,结合实验对于平滑区选取1.2的分数阶全变差进行优化求解。图像像素x(i,j) 在本文的分数阶差分定义为G-L定义[9]取前K项近似,其水平和垂直方向的表达式分别为
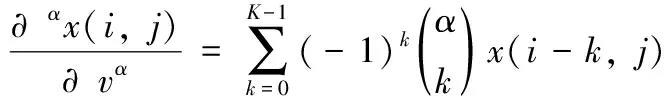
(4)
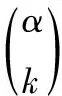
(5)

(6)
1.2 基于NLTV的非盲去模糊模型
自然图像中存在高度冗余的相似性信息,即存在着许多相似特性的区域,且其常常以周期形式出现。根据纹理细节具有的冗余相似性,利用图像本身的信息来用于合成图像的纹理细节,基于非局部相似性的NLTV进而成为图像修复和重建的另一种方法。图像非盲去模糊的NLTV模型如下
(7)
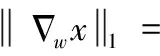
(8)
其中,μ表示正则项系数,w(x(m,n),x(i,j))表示以两个像素点x(i,j)、x(m,n)为中心的两个区域图像间的相似性权重,其大小取决这两像素邻域相似性大小,两像素邻域相似性越大则其相似性权重也越大,且其取值在0到1之间。
1.3 结合FOTV和NLTV非盲去模糊模型
综合NLTV和FOTV模型各自的优势,将之运用到图像去模糊重建中是本文研究的起点。本文首先采用GGES将图像x分解成平滑、边缘和纹理3个部分,其中边缘和平滑区域作为xs,纹理细节作为xd,以barbara图像为例,分解结果如图2所示。用FOTV约束xs作为一个正则项,用NLTV模型约束xd作为另一个正则项,加上图像数据保真项得到本文的数学模型如下
(9)

图2 GGES分解barbara结果注:(a)原始图;(b)原始图xs部分;(c)原始图xd部分;(d)模糊噪声图;(e)模糊噪声图xs部分;(f)模糊噪声图xd部分
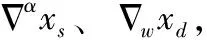
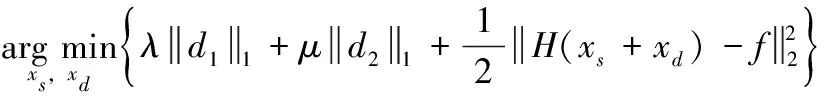
(10)
2 求解算法
对于上式两个正则项都是不可微的凸函数优化问题,本文采用ADMM[2,10]和BOS[3]算法分别对xs和xd进行逐步求解。
2.1 ADMM求解xs
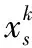
(11)
利用式(11)的约束条件,采用惩罚方法将两者的差的L2范数的平方作为惩罚项,从而将上述有约束的优化问题转为无约束优化问题
(12)

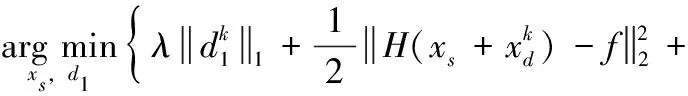
(13)
(14)
由于上式等号右边都是二次项,通过对xs求导,得到关于xs导数为0方程
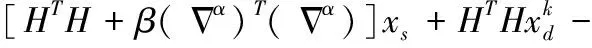
(15)
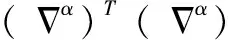
(16)
式中:∘表示点乘,F、F-1分别代表傅里叶变换和傅里叶反变换。
(17)
采用软阈值方法[11]求解d1k+1
(18)
2.2 BOS求解xd
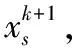
(19)
为了加速求解xd,运用变量分裂的思想引入辅助变量v,令v=xd, 根据BOS迭代策略上述问题转为
(20)
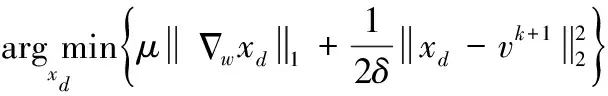
2.3 算法总结
先后对两个子问题的求解,得到表1的FNLTV算法。

表1 FNLTV算法
3 实 验
3.1 实验参数
本文实验选取了4幅包含了平滑、边缘和纹理细节部分大小为256×256像素的经典数字图像:barbara、lena、fingerprint、cameraman。实验原始图像如图3所示。

图3 原始实验图注:(a)barbara;(b)lena;(c)cameraman;(d)fingerprint
本文所有实验基于Matalb R2012b 8.0.0.783完成,实验的计算机处理器为Intel I3-2350M (2.30 GHz),RAM为2 GB,实验附加噪声设置为加性高斯噪声,且分为3个不同级别。实验选取了4种比较常见的模糊核BK(blur kernel):角度为135,长度为15的运动(motion)模糊BK1;尺寸为21×21,标准差为2的高斯(Gaussian)模糊BK2;尺寸为5的圆盘(disk)模糊BK3;尺寸为9的均匀(ave-rage)模糊BK4。本文算法的参数众多:tol、α、K、λ、β、μ、δ,经过反复实验,将参数设置成如下:tol=0.001、α=1.2、K=17、δ=1.1;FOTV和NLTV的正则项参数和惩罚项参数在噪声水平不同的情况下也要随之变化。根据实验调试结果,λ、β和μ的选取情况见表2。
3.2 实验效果
为了直观且有针对性地具体地验证本文算法的有效性,采用文献[9]提出的阶次为1.2的FTVd算法、文献[12]提出的TVd算法和以及文献[3]提出的NLTV-pbos,简称NLTV算法作为3种对比算法进行实验。以lena 图像在噪声级别为30 dB时去高斯模糊的情况作为例子,在视觉上验证本文算法相对于单一的分数阶全变差模型和传统的全变差模型的优越性,对比了3种算法的去模糊效果和细节图,如图4、图5所示。
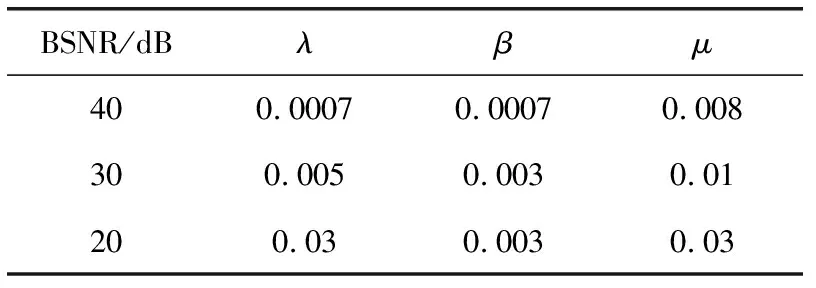
表2 不同噪声级别实验参数选取

图4 lena对比实验注:(a)lena原始图;(b)高斯模糊图;(c)TVd复原图(psnr=21.75);(d)FOTV复原图(psnr=22.61);(e)NLTV复原图(psnr=21.21);(f)本文算法图(psnr=22.71)

图5 lena细节图注:(a)原始细节;(b)高斯模糊细节;(c)TVd复原细节;(d)FTVd复原细节;(e)NLTV复原细节;(f)本文算法细节
由图4、图5可知,NLTV复原图较暗,效果最差;本文算法没有明显的阶梯效应,较FTVd算法效果提高不明显,但根据细节图本文算法恢复的头发细节更多,也去除了更多的噪声。
3.3 实验数据
为了客观地验证本文算法的有效性,以峰值信噪比PSNR(peak signal-to-noise ratio)为指标进行实验,对4幅实验图像进行噪声级别分别为BSNR=40 dB、30 dB、20 dB时4种模糊核的去模糊实验,得到的实验数据见表3~表5。
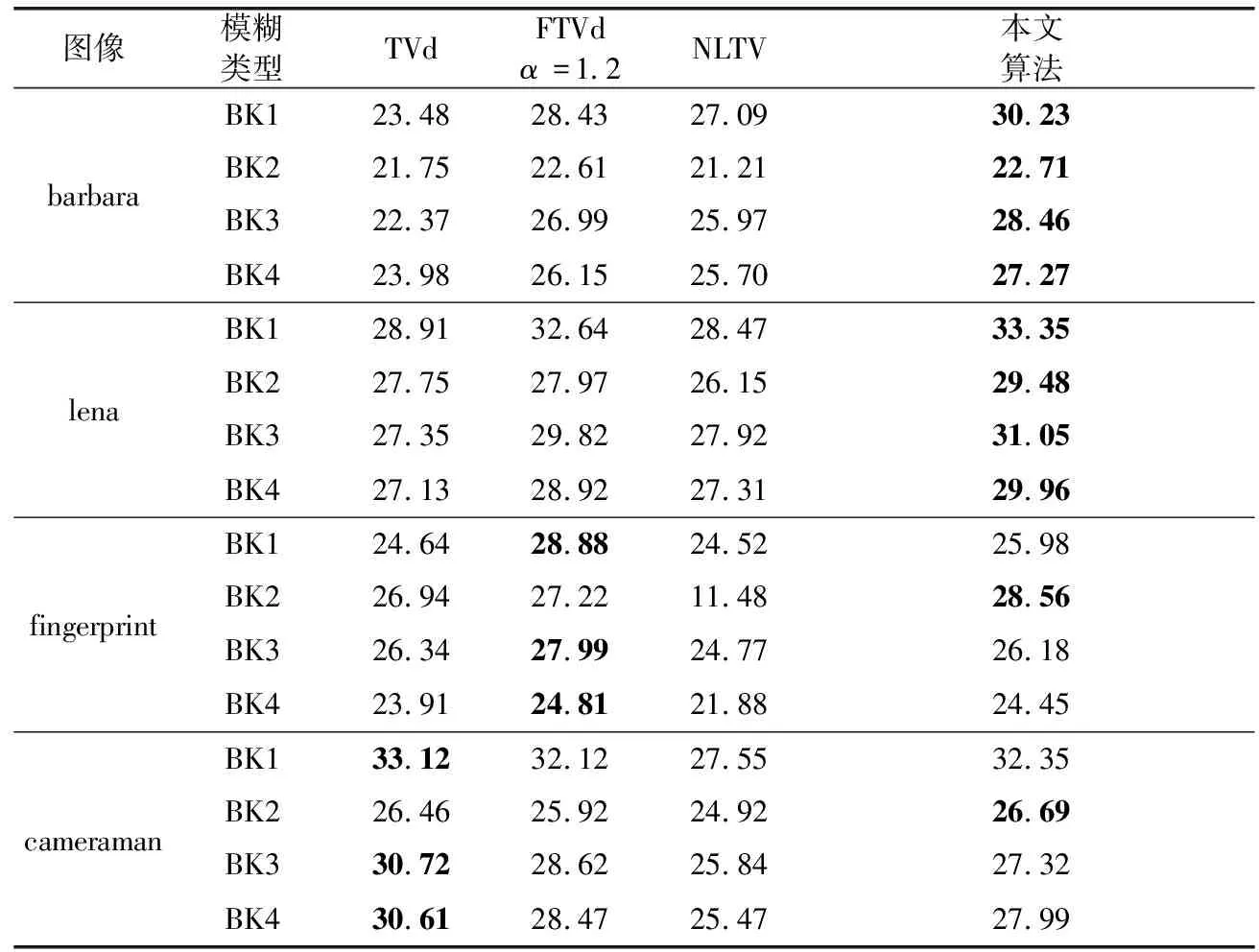
表3 BSNR=40 dB时不同图像各算法非盲去模糊PSNR(dB)对比
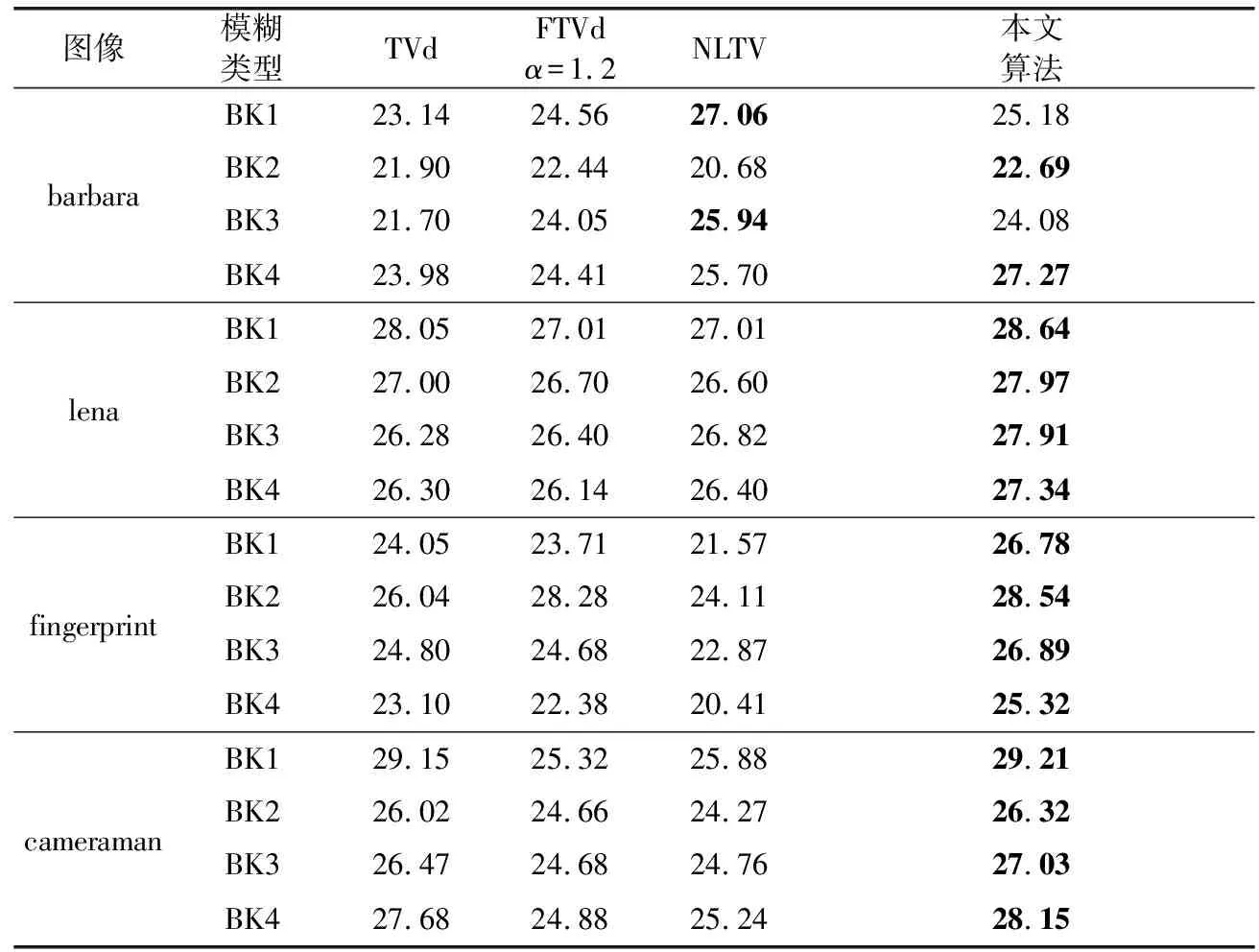
表4 BSNR=30 dB时不同图像各算法非盲去模糊PSNR(dB)对比
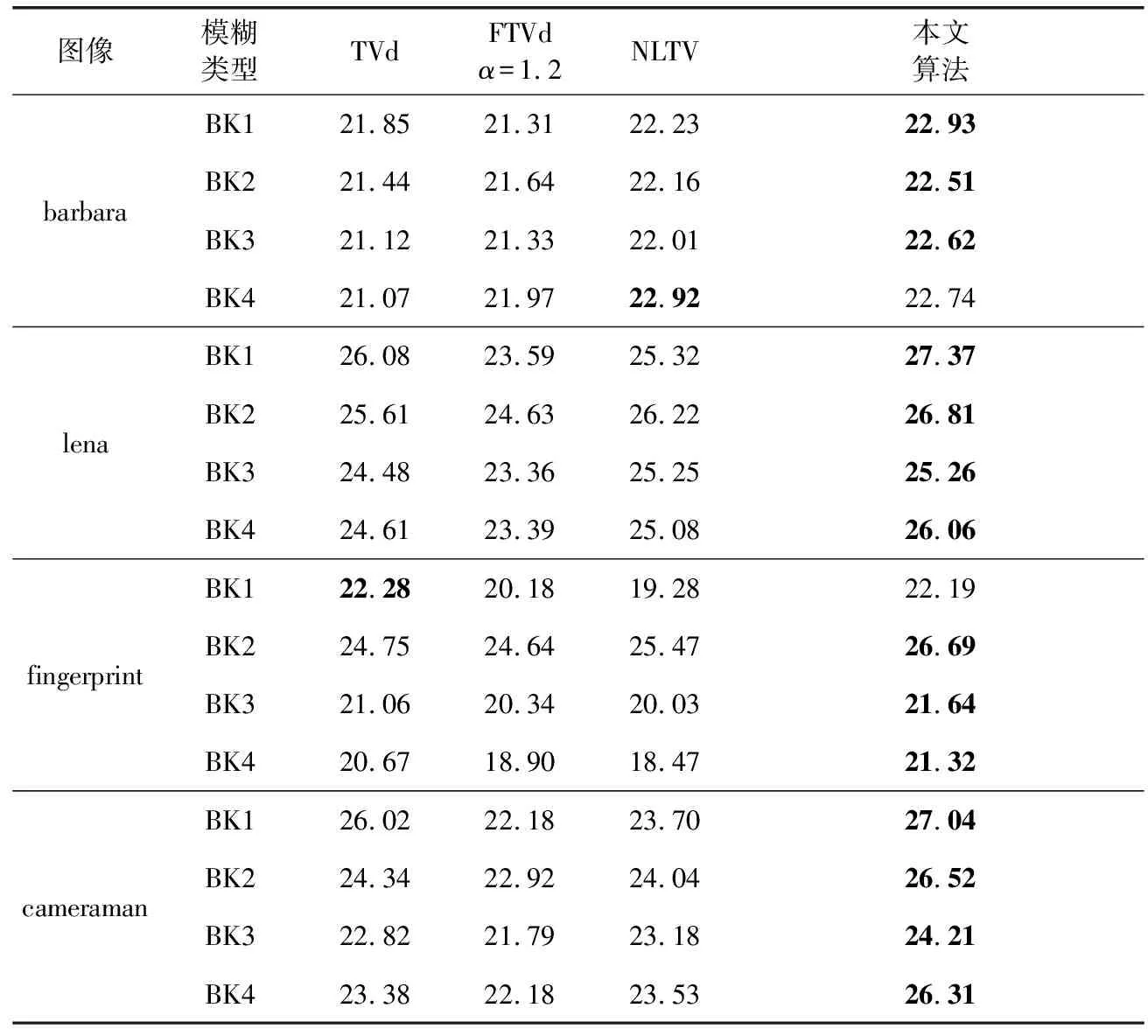
表5 BSNR=20 dB时不同图像各算法非盲去模糊PSNR(dB)对比
根据实验数据,对比其它3种算法,对于3种不同级别的附加噪声4种去模糊效果来看,本文算法具有一定程度的优势,尤其是去高斯模糊,均具有最佳PSNR值,具体表现为:当BSNR=40 dB时,lena和barbara图的4种去模糊效果本文算法都比较优秀,总能具有最佳PSNR值,对于纹理细节相对较多的fingerprint图,本文算法只对去高斯模糊具有最优的PSNR值,其它3种去模糊效果不如FTVd效果好;对于纹理细节相对较少的cameraman图,本文算法去高斯模糊PSNR值最佳,其它3种模糊传统TV表现最佳;当BSNR=30 dB、20 dB时,4幅图像4种去模糊效果本文算法都表现较好,基本能具有最佳的PSNR值。
4 结束语
本文算法一定程度地结合了FOTV和NLTV模型在图像非盲去模糊重建方面的优势,一方面利用了FOTV算法消除阶梯效应的特性,分数阶次的适当选取避免了过平滑现象,同时还保留了TV模型强大的边缘保护能力;另一方面利用了NLTV算法保留纹理细节的优势,充分运用了图像本身结构信息。从实验结果来看,对比单独的FOTV和NLTV算法,虽然不是对所有图像均表现了绝对的优势,但总体上本文算法优势明显,阶梯效应和过平滑效应均得到一定的避免,且较好地恢复了图像的纹理细节。但由于本文算法涉及两种TV模型,正则化参数和惩罚参数众多,因此程序调试的周期相对比较长,这也是本文的最大不足之处,需要做进一步的参数自适应的研究和改进。
