电网输电线路故障监控定位算法

陈 岩，李晓卉+，丁月民，蔡 彬

(1.武汉科技大学 信息科学与工程学院，湖北 武汉 430081；2.天津理工大学 计算机与通信工程学院，天津 300384)

0 引 言

作为电力系统的重要组成部分，电网传输线路故障发生后需第一时间确定故障点的位置，避免产生更大的经济损失[1]。现代智能电网(smart grid)将先进的传感技术、控制技术和通信技术集成于一体[2,3]，采用无线传感器节点监控故障信息，并通过无线传感器网络(wireless sensor network，WSN)将故障信息传输到电网控制中心，该方法大大提高了电网输电线路故障自动监控的能力[4]。

作为WSN中的一种距离无关(range-free)定位算法，距离向量-跳段(distance vector-hop，DV-Hop)算法应用在电网输电线路故障监控时，由于智能电网输电线间距远小于传感器节点通信半径，当某节点与垂直方向上的节点通信时，其与任一垂直方向上节点的跳数都为1。因此，在计算位于垂直方向的节点间距离时就会产生一定误差。在智能电网背景中，传感器节点都安装在传输线上，大大增加了锚节点的共线几率，采用三边测距法求解未知节点坐标存在较大误差。当采用极大似然估计时，由于未知节点与锚节点之间的估算距离与实际距离之间存在误差，在方程组相减时会产生累积误差，影响定位精度[5-9]。

为解决以上问题，本文提出一种适用于电网输电线路的故障监控定位算法(localization algorithm for the fault monitoring of power transmission line，SG iDV-Hop)。该算法在原始DV-Hop的基础上，采用最小均方差(minimum mean square error，MMSE)计算锚节点平均跳距，并引入误差因子对其进行修正。实际电网输电线路并不都是水平的，而是呈一个角度排列，因此将输电线倾斜一个角度，线上的传感器节点以交错的形式排列部署。采用二维双曲线法求解未知节点坐标，一方面减少了由估算距离误差带来的累积误差，另一方面避免了方程组直接相减造成未知节点坐标二次项损失。

1 基于WSN的电网输电线路故障监控

智能电网输电线路故障监控中WSN体系结构如图1所示，传感器节点监测的数据经过多跳后路由到汇聚节点，最后通过互联网和卫星到达监控中心，用户可以在监控中心收集并分析有关输电线路的监测数据。

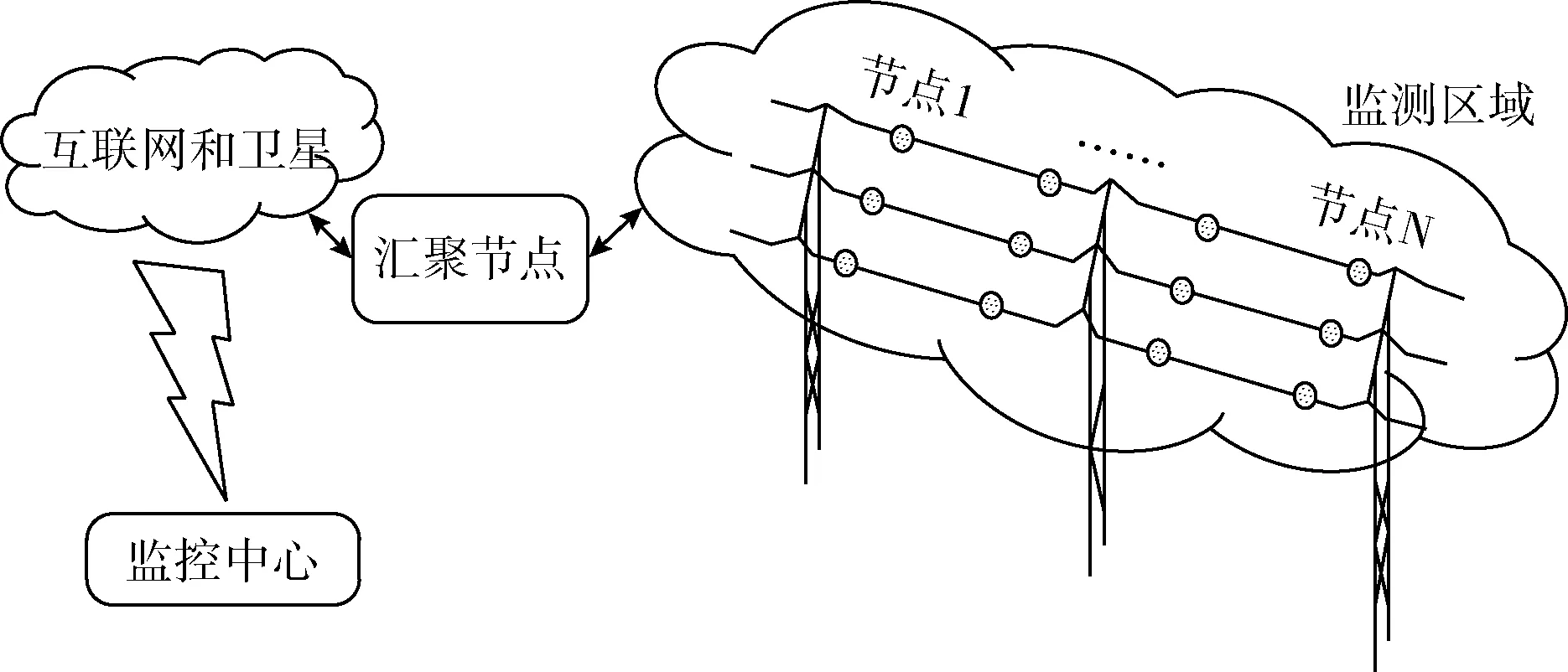
图1 基于WSN的智能电网输电线路故障监控

一般输电线路上的传感器网络部署如图2所示。每根线的斜率k=tan10且线与线的间距相等，同一根线上的节点等距离分布，不同线上的节点交错分布。由于受到成本等方面的限制，l的长度要远大于w，这就使得节点的通信半径满足R≥l，才能实现节点间正常通信。

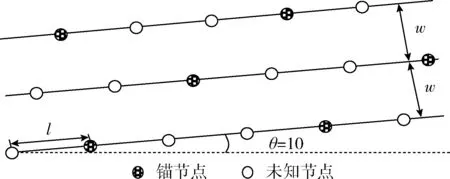
图2 智能电网输电线路上的WSN部署

2 SG iDV-Hop定位算法

首先，SG iDV-Hop算法采用MMSE计算锚节点间平均跳距[10]，结合锚节点间最小跳数算出锚节点间的估算距离并以锚节点间实际距离与估算距离之差作为误差因子，对锚节点间平均跳距进行修正。然后，在估算未知节点到锚节点的距离时，引入一个与其最小跳数相关的动态权值对未知节点到锚节点的平均跳距进行修正，再结合二者间最小跳数算出未知节点到锚节点的距离。最后，以二维双曲线法估算未知节点坐标，在求得未知节点坐标的同时还会得到一个与未知节点坐标相关的参数因子，利用该参数因子对估算坐标进行更新得出未知节点的最终坐标[11]。

SG iDV-Hop初始化时，锚节点i将包含自身位置信息(xi，yi，hi)的数据包广播至网络中，其中(xi，yi)为锚节点坐标，hi为锚节点跳数信息初始化值为0。接收节点记录其到每个锚节点的最小跳数，忽略来自同一个锚节点的较大跳数的数据包，然后将跳数加1并转发给邻居节点。由此，网络中所有节点都能获得每个锚节点的坐标以及二者间最小跳数。

2.1 锚节点间平均跳距

为了使锚节点间平均跳距更加接近实际值以进一步减小累积误差，采用最小均方差计算M个锚节点间平均跳距，公式如下所示

式中：dij为锚节点i、j间欧氏距离，hij为锚节点i、j间最小跳数。

锚节点i、j间的估算距离如下所示

则锚节点i、j估算距离与欧氏距离之间的误差为

因此，锚节点i的平均每跳误差为

(1)

2.2 未知节点到锚节点间估算距离

在计算未知节点x到锚节点的估算距离之前，先对未知节点x到锚节点的平均跳距进行修正。引入一个与其最小跳数相关的动态权值λ，则未知节点与锚节点间平均跳距修正公式如下

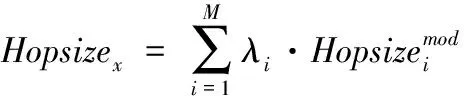
其中，hopi为未知节点x到锚节点i的最小跳数。则未知节点x到锚节点i的估算距离公式如下

(2)

2.3 未知节点坐标及更新

(3)

将式(3)展开如下

(4)

令k=x2+y2，可将式(4)整理成矩阵方程形式

AX=b

(5)

其中

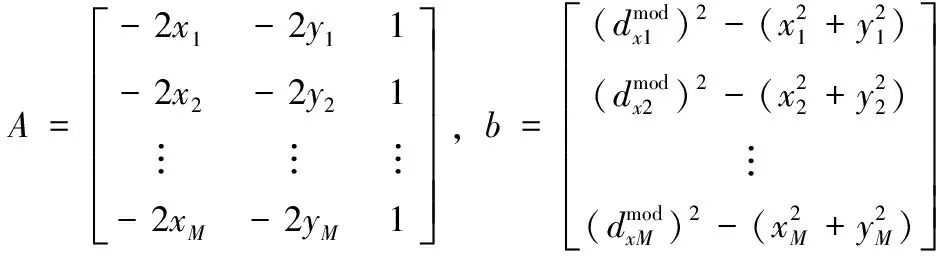
采用最小二乘法对矩阵方程组(5)求解得

X=(ATA)-1ATb

(6)

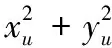
因此，通过参数k得到的未知节点坐标(xe，ye)为

(7)

最后，结合式(6)得到的坐标(xu，yu)和式(7)得到的坐标(xe，ye)以求均值的方式更新未知节点坐标。在计算过程中，采用最小二乘法求解得到的坐标(xu，yu)的权重是通过参数k计算得到的坐标(xe，ye)的两倍。未知节点坐标更新公式如下

(8)

图3给出SG iDV-Hop算法流程，描述如下：

图3 SG iDV-Hop算法流程

步骤1 算法初始化

初始化网络，配置传感器监测区域、节点总数、锚节点比例以及节点通信半径等信息。锚节点将包含自身信息(xi，yi，hi)的数据包广播至网络中。

步骤2 未知节点接受数据包

未知节点接收来自锚节点的数据包，并保存其到每个锚节点的最小跳数。未知节点收到3个锚节点的数据包后开始定位，否则定位失败。

步骤3 锚节点间平均跳距

为了减少节点垂直通信产生的误差，采用式(1)计算锚节点间平均跳距。

步骤4 未知节点到锚节点间估算距离

引入动态权值λ，对未知节点到锚节点的平均跳距进行修正，通过式(2)计算未知节点到锚节点的距离。

步骤5 未知节点坐标及更新

为了减小累积误差，采用二维双曲线法计算未知节点坐标，并通过式(6)最小二乘法求解。为进一步提高定位精度，通过式(8)更新节点坐标。

3 仿真结果分析

为了验证SG iDV-Hop算法在智能电网传输线路故障监控中的定位效果，在MATLAB 2014a上对SG iDV-Hop算法坐标更新前后的结果和原始DV-Hop算法的结果进行对比仿真。5根输电线用5个斜率相同截距不同的函数表示，见表1。其中，斜率k=tan10，每个函数所对应的x的初值分别为0、2、4、6、8且每隔10 m取一个点。当节点总数为200时，每个输电线上有40个点，故x在[0,400]范围内取值，由于斜率的存在此时节点的分布区域约为400 m×80 m。以此类推，因此节点总数不同则节点的分布区域也不同。

表1 输电线函数表达式

假设所有节点的通信半径相同且通信范围为完整的圆形，定位误差公式定义如下

(9)

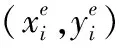
3.1 锚节点比例对定位误差的影响

锚节点比例对定位误差的影响如图4所示。当节点总数为200，节点通信半径为15 m，锚节点比例为5%时，采用3种算法得到的定位误差均比较高。SG iDV-Hop算法坐标更新前后的定位误差分别为0.89和0.84，而原始DV-Hop算法的误差高达0.98。锚节点比例为5%时，仿真区域内锚节点分布较为稀疏，缺乏足够的锚节点导致节点间平均每跳距离误差增大，由于累积误差的存在导致定位精度大大降低。随着锚节点比例逐渐增多，区域内锚节点密度逐渐变大，未知节点与锚节点之间的跳数逐渐减小。因此，二者之间的估算距离逐渐接近其欧氏距离。当锚节点比例增加到25%时，SG iDV-Hop算法坐标更新前后的定位误差分别为0.44和0.42，而原始DV-Hop算法的定位误差仍在0.5以上。

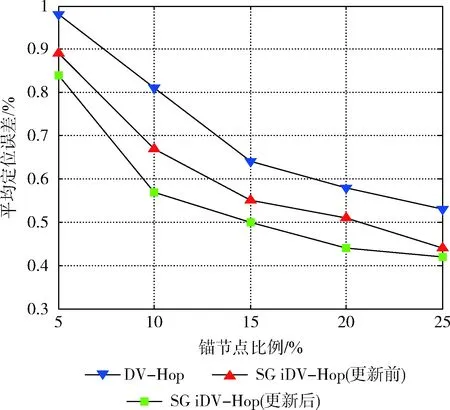
图4 锚节点比例对定位误差的影响

3.2 节点通信半径对定位误差的影响

图5描述了当节点总数和锚节点比例一定时(节点总数为200，锚节点比例为10%)，节点通信半径对定位误差的影响。随着节点通信半径从15 m逐渐增大到35 m，所有算法的定位误差均呈下降趋势，而SG iDV-Hop算法坐标更新后的定位精度在不同通信半径下都是最高的。当通信半径为15 m时，SG iDV-Hop算法坐标更新后的定位精度比原始DV-Hop提高大约27%。随着通信半径不断增加，3种算法的定位误差逐渐接近，当通信半径增加到35 m时，原始DV-Hop的定位误差为0.61，与SG iDV-Hop算法坐标更新前后的定位误差非常接近。这是因为当通信半径增加时，网络连通率大大增加，节点之间的估算距离越来越接近其欧氏距离，在DV-Hop算法中累积误差对定位精度产生的影响逐渐减小，因此三者的定位误差逐渐接近。

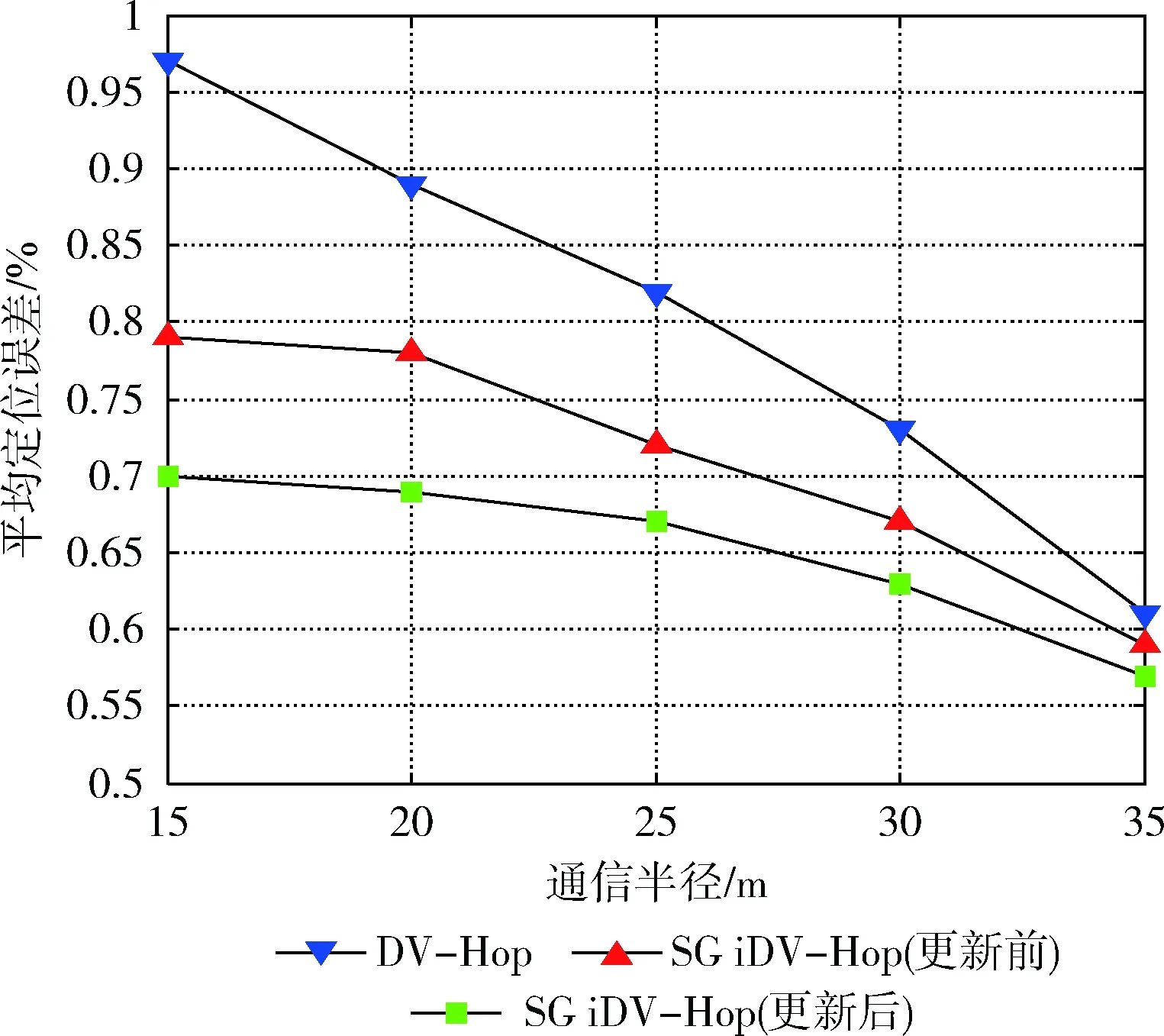
图5 节点通信半径对定位误差的影响

3.3 节点总数对定位误差的影响

当节点通信半径为15 m，锚节点比例为10%时，节点总数对定位误差的影响如图6所示。尽管SG iDV-Hop算法坐标更新前后的定位误差在节点总数为300时稍微有所下降，但总体仍呈上升趋势。在节点总数逐渐增加的过程中，根据表1可看出节点的分布区域也在逐渐变大。在锚节点比例一定的情况下，节点总数增多导致节点分布区域变大，区域内锚节点密度逐渐减小，因此定位误差变大。与原始DV-Hop算法相比，SG iDV-Hop算法在不同节点总数下均能明显减小定位误差。

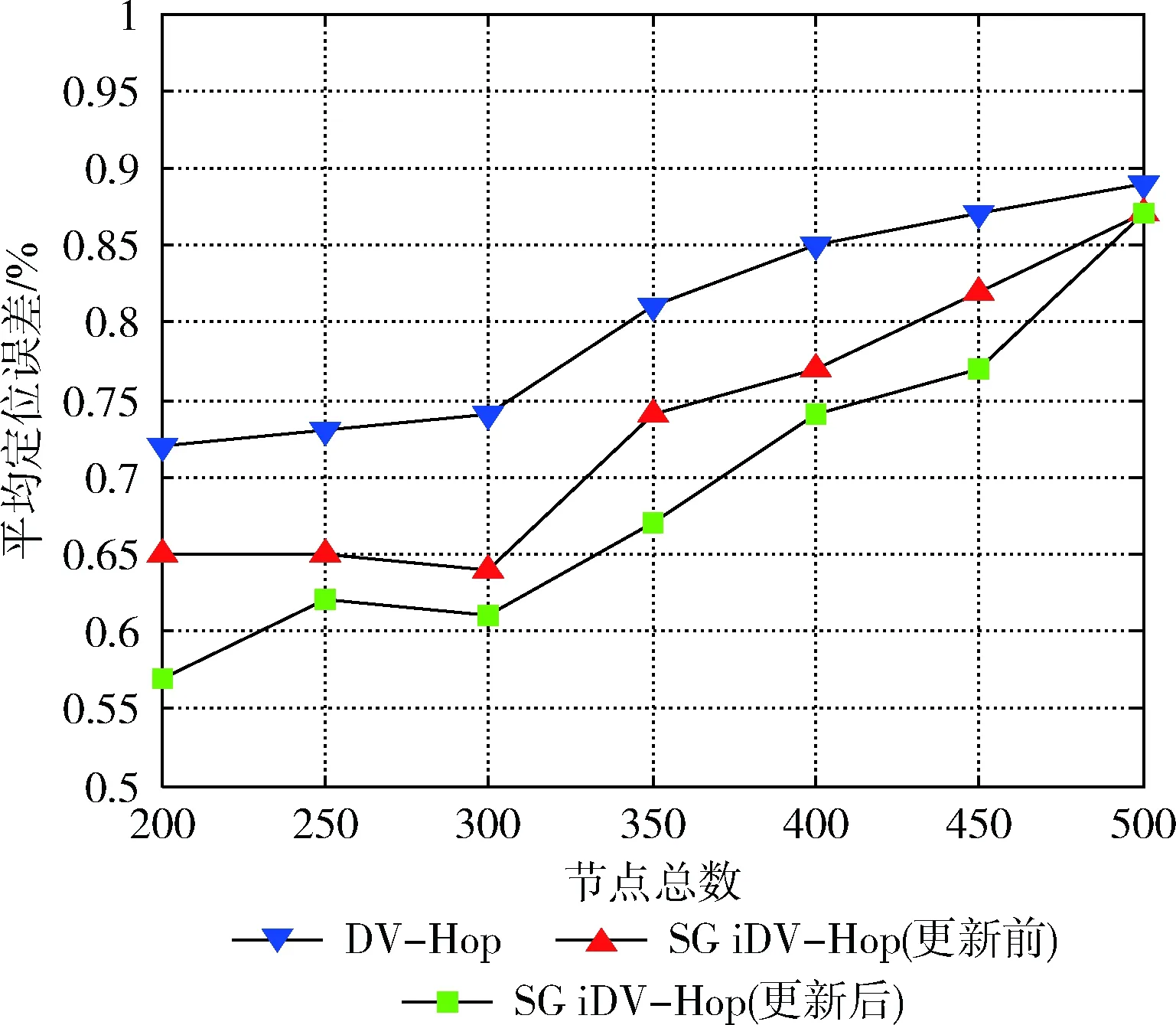
图6 节点总数对定位误差的影响

4 结束语

本文针对智能电网输电线路中故障监控问题，对原始DV-Hop算法进行改进，提出了SG iDV-Hop算法。在减小节点垂直通信带来的误差方面，采用最小均方误差计算锚节点间平均跳距并引入误差因子进行修正，计算未知节点与锚节点的距离时引入一个与其最小跳数相关的动态权值对未知节点平均跳距进行修正。在减小锚节点共线带来的误差和累积误差方面，合理设计智能电网输电线路上的WSN部署结构，采用二维双曲线法计算未知节点坐标并引入参数因子对其进行更新。3种不同情况下的仿真结果表明，SG iDV-Hop算法均能明显改善定位误差，尤其是在更新坐标信息后定位精度更加准确。本文目前研究了二维坐标情况下的未知节点坐标定位问题，并没有针对三维模型进行分析，并且SG iDV-Hop算法的计算复杂度较高。在后续的工作中，主要针对算法的计算复杂度做出改进并将其应用到三维模型中。