基于邻域LBP算子与块截断编码的图像哈希算法
2018-07-19王彦超
王彦超
(平顶山教育学院 计算机系,河南 平顶山 467000)
0 引 言
随着计算机技术的快速升级,使得市场上出现了越来越多的图像编辑工具,攻击者通过这些工具,可随意地改变图像内容,并且无视觉篡改痕迹,导致用户无法辨别图像的真伪,对其信息安全带来了巨大负面影响[1,2]。为此,为了实现对用户接收图像的内容进行真伪判别,学者们提出了相应的图像哈希算法[3,4]。如唐振军等[5]提出了基于PCA特征距离的图像哈希算法,通过预处理与分块随机组合处理,获取二次图像,再利用PCA技术,对二次图像进行压缩与量化处理,获取低维哈希序列。虽然该技术能够降低哈希序列的空间维数,但分块随机组合处理无法提取图像的鲁棒特征,使得哈希序列的敏感性与安全性不佳,尤其是难以识别旋转几何变换攻击。王彦超等[6]提出了基于数据投影降维机制与对称局部二值模式的紧凑图像哈希算法,通过设计对称局部二值模式,来提取图像的鲁棒特征,通过相应的量化函数,获取紧凑哈希序列,但称局部二值模式忽略了图像像素内在的空间关系,使其描述能力不足,无法充分获取鲁棒特征,使其哈希鲁棒性不佳。Tang等[7]提出了基于颜色矢量角度与Canny检测算法的图像哈希技术,通过插值技术与低通滤波预处理图像,并从预处理图像中提取颜色矢量角度与边缘特征,通过组合二者,输出哈希序列。然而,该技术直接利用提取的颜色矢量角度与边缘特征来生成哈希,使其空间维数较高,且Canny检测算法的稳定不佳,易获取伪特征,降低了哈希序列的鲁棒性。
针对上述问题,本文提出了基于块截断编码与邻域空间LBP算子的鲁棒图像哈希算法来改善哈希序列的敏感性与鲁棒性。利用插值技术与Gaussian低通滤波来预处理图像,以规范图像尺寸,使其对缩放、噪声攻击具有理想的鲁棒性;基奇异值分解SVD(singular value decomposition)机制,获取二次图像;利用块截断编码机制处理二次图像,获取高、低电平矩阵以及二值量化图像。设计邻域空间LBP算子,提取二值量化图像的鲁棒特征,输出特征矩阵。构造量化函数,对高、低电平矩阵进行压缩,输出紧凑二值序列;引入主成分分析处理特征矩阵,形成二值特征序列。通过组合高、低电平矩阵,以及特征矩阵3个对应的二值序列,获取图像哈希。最后,测试了所提哈希机制的鲁棒性与ROC特性。
1 块截断编码
块截断编码[8]主要是用于压缩图像,通过将初始图像分割为非重叠子块,对于每个子块,利用块截断编码处理后,初始图像被编码为二进制位图与两个均值,其主要步骤如下:
(1)令输入图像为f0(x,y),其尺寸为M×N;将其分割为非重叠子块Zi,其尺寸为k×k(k值一般取4或8)。最后,计算每个Zi的像素均值X
(1)
式中:xij代表第i个子块中位于(i,j)处的像素值;m×n像素的极限位置;X为子块的像素均值。
(2)根据式(1)计算,得到子块的像素均值X,将子块中的所有像素划分为两类:C0,C1。其中,C0为像素值低于均值X的像素所构成的集合;C1代表像素值大于均值X的像素所构成的集合。通过对C0,C1中的像素赋值0或者1,从而可得到位图BM。也就是当子块像素值大于均值X时,其对应的BM值为1,形成C1;反之,则为0,获取C0。位图BM如下
(2)
式中:bij为二进制位图BM中的(i,j)位。
(3)根据每个二值子块的像素均值X与标准差σ,计算其重构电平αij,βij,以复原图像
(3)
(4)
其中,nij为子块中的像素数量;σij子块中的像素标差;k2为子块尺寸。
在执行块截断编码过程中,利用重构电平αij,βij来替代子块中的零值像素与其它像素值,从而产生一个与初始子块视觉相同的编码图像块。
(4)为了与式(3)、式(4)一致,其一阶矩μij、二阶矩vij需要与编码图像块相同
k2×uij=(k2-nij)αij+nij×βij
(5)
(6)
其中,μij为一阶矩;vij为二阶矩。
根据上述描述可知,编码二值子块,以及重构电平αij,βij能够真实反映初始子块的鲁棒特征。为了详细解释块截断编码机制,本文取k=4,也就是子块的尺寸为4×4,其编码过程如图1所示。根据子块像素值,可得到其均值X=115,标准方差σ=115。根据X,σ,对子块进行编码后,获取位图BM;同时,该子块的像素数量为8,依据式(3)、式(4)可得,获取低、高重建电平αij,βij分别为37,139。再利用αij=37、βij=139分别替代位图BM中的零值、非零元素,输出右边的编码图像子块。
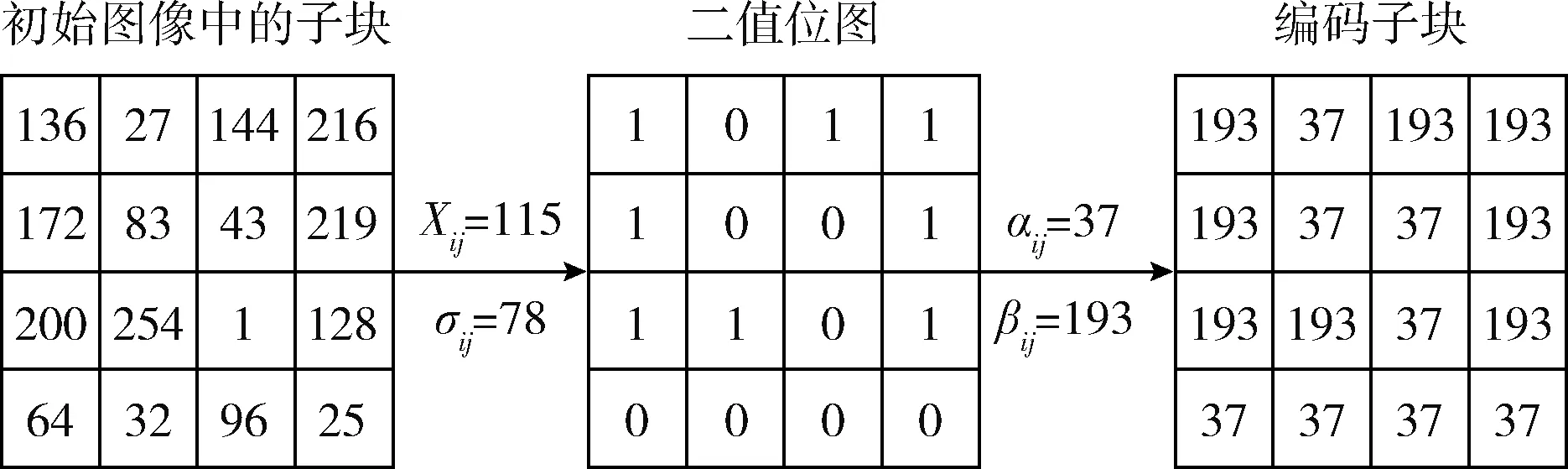
图1 块截断编码过程
2 本文图像哈希算法
本文鲁棒图像哈希技术过程如图2所示,主要有:①图像预处理;②基于块截断编码与邻域空间LBP算子的鲁棒特性提取;③基于主成分分析的紧凑哈希生成与认证。
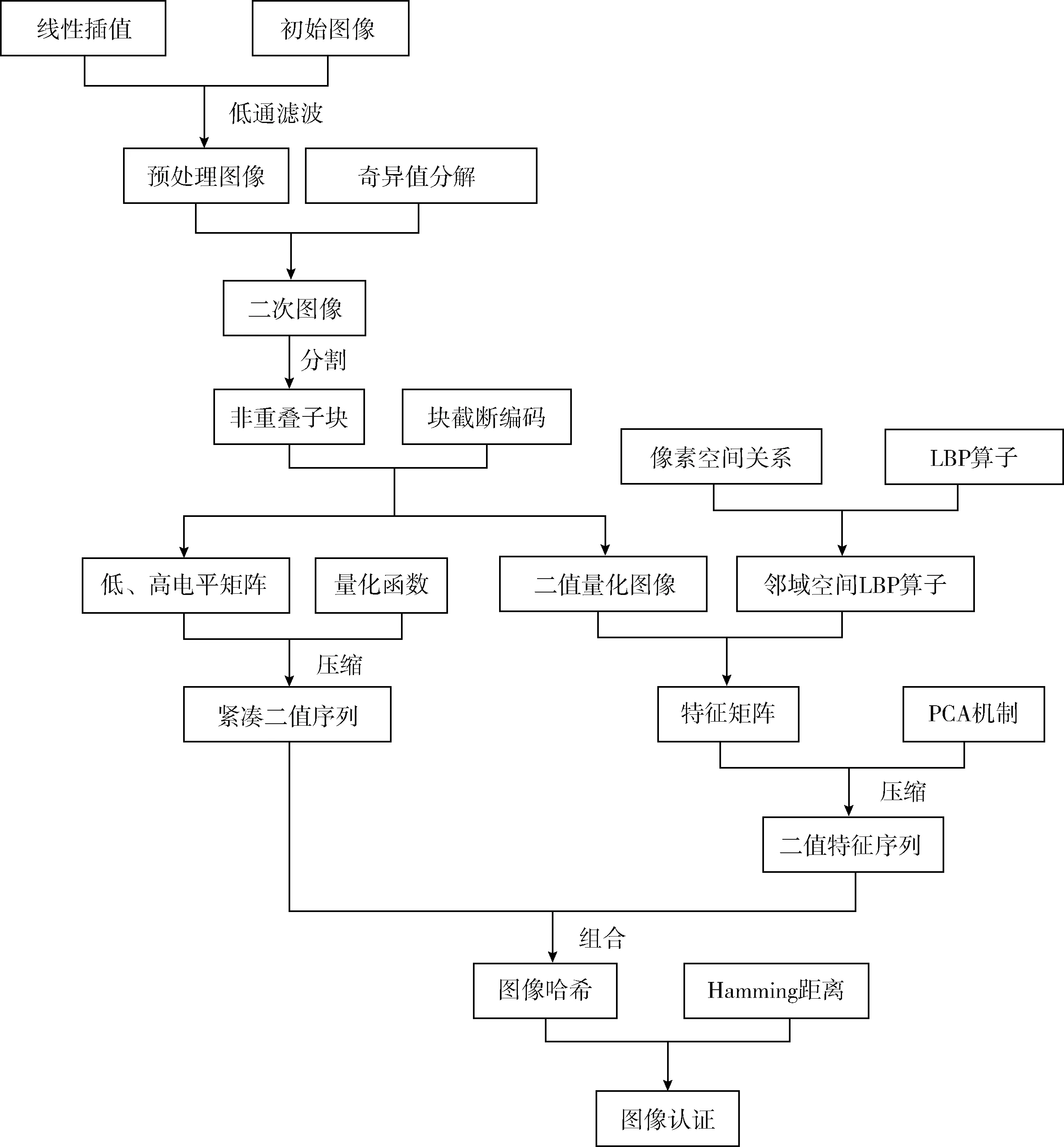
图2 本文紧凑哈希算法过程
2.1 图像预处理
图像预处理[9]时图像哈希必不可少的过程,对于图像的输入图像,能够固定其尺寸,增强哈希序列对缩放的鲁棒性能。为此,本文引入2D线性插值[10]、高斯低通滤波[11]以及奇异值分解[12],形成预处理机制,使其具有一个固定的哈希长度。其中,二维插值技术函数为[10]
(7)
(8)
其中,x0,x1是初始起点;y0,y1代表x0,x1的插值结果。
经过式(7)、式(8)插值后,以规范图像尺寸;再利用高斯低通滤波[11]来平滑插值图像,增强哈希序列对噪声的稳健性,它主要是通过卷积掩模来实现。令G(i,j)是卷积掩模在坐标(i,j)处的元素,其函数为[11]
(9)
式中:δ是卷积掩模中所有像素的标准差;M×M为图像尺寸;(i,j)为像素坐标;e为指数函数。
初始图像f0(x,y)经过式(7)~式(9)处理后,获取尺寸为M×M的平滑图像f1(x,y),增强哈希所尺度与噪声的鲁棒性。随后,对f1(x,y)完成分割处理,获取一系列尺寸为k×k的非重叠子块Bij(i,j=1,2…M/k)。 则f1(x,y) 变为
(10)
通过式(10),将平滑图像f1(x,y)变为若干个非重叠子块Bij,以便于奇异值分解的计算。
为了改善哈希算法对JPEG压缩、旋转等攻击的鲁棒性,本文引入奇异值分解[12]SVD(singular value decomposition),充分利用奇异值的稳定不变性来获取视觉质量较高,且鲁棒性更强的二次图像。SVD模型为
X=S·V·D
(11)
式中:S,D为输入图像X的k×k维正交矩阵;V为输入图像X的k×k维对角矩阵,包含k个奇异值。
再根据式(11)处理平滑图像Bi,j,可得
Bi,j=Si,j·Vi,j·Di,j
(12)
式中:Si,j为输入平滑图像Bi,j的k×k维正交矩阵;Di,j是由平滑图像Bi,j的k×k正交矩阵中;Vi,j是平滑图像Bi,j的对角矩阵。
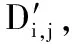
(13)
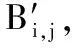
(14)
依据式(14),将预处理图像演变为二次图像,有效增强其抗旋转的能力,进一步改善哈希的鲁棒性。
2.2 基于块截断编码与邻域空间LBP算子的鲁棒特征提取
获取二次图像I后,需要从I中提取整个图像的鲁棒特征来生成哈希。为此,本文通过设计邻域空间LBP算子,并联合块截断编码来实现此目的,其过程如图3所示。
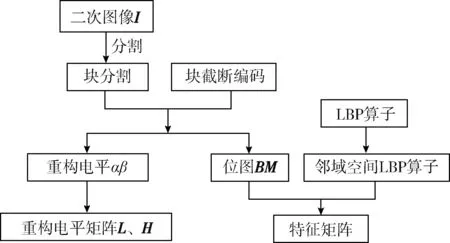
图3 图像鲁棒特征的提取过程
首先,将二次图像I分割为非重叠子块,每个子块的尺寸为k2×k2,用Fi,j来表示
(15)
式中:Fi,j为二次图像I对应的子块。
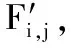

(16)
(17)
根据块截断编码机制,可输出二次图像I的3个矩阵L,H以及BM。随后,本文在LBP(local binary pattern)算子[13]基础上,考虑图像像素内在的空间关系,设计了邻域空间LBP算子,提取位图BM的鲁棒特征。
LBP算子[13]具有较好地旋转与灰度不变性,通常用来提取图像特征。但是,LBP主要是考虑单个区域内的特征,其模型为[12]
(18)

(19)
其中,S(x)是中心像素与其邻域点的灰度差;gc为中心像素;gi是其它位置的像素;LBPR,P代表半径为R,包含P个邻域像素的LBP模式。常见的3种LBP算子如图4所示。
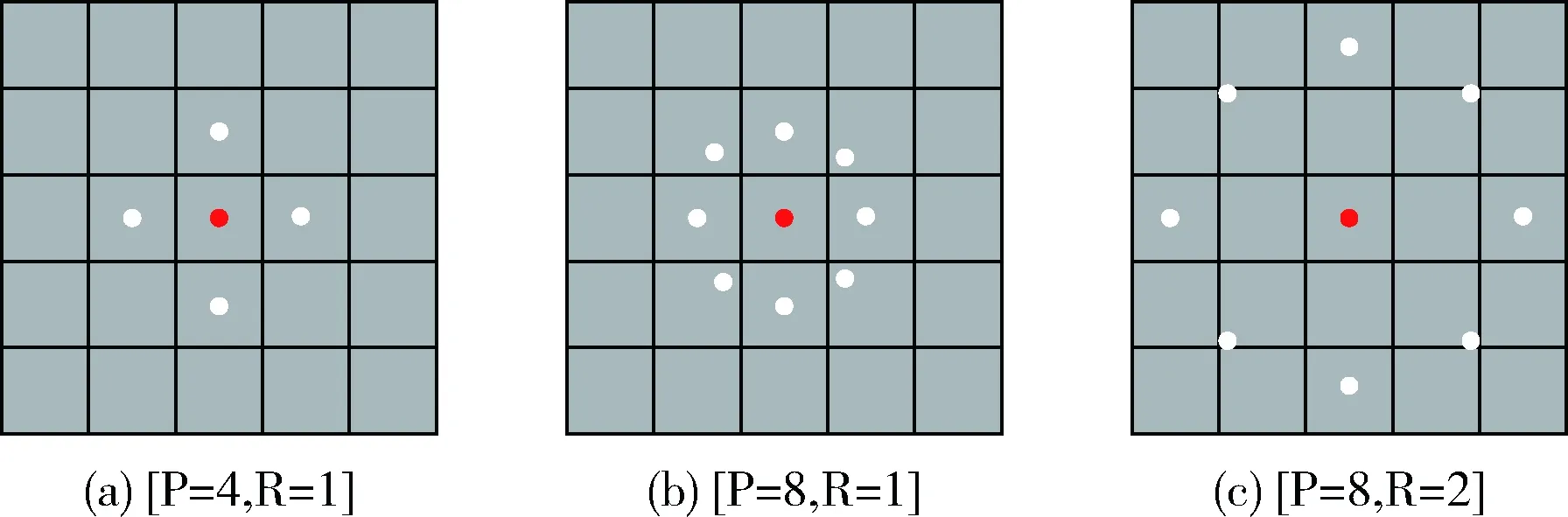
图4 不同尺度下的LBP算子
通过利用式(18),即可提取图像的特征;但是,依据式(18)可知,当邻域像素数量P的不断变化时,其可输出2P种LBP模式;随后,估算所有LBP的直方图,将其视为LBP特征。但是,这种LBP算子没有考虑图像内在的空间关系,使其对特征的描述能力不佳。
为此,本文将图像的空间关系引入到式(18)中,设计了邻域空间LBP算子。首先,任意选取两个像素点p1,p2来估算二者与中心像素的偏差Dp1i,Dp2i
Dp1i=Ip1(gi)-Ip1(gc)
Dp2i=Ip1(gi)-Ip2(gc)
(20)
式中:Ip1(gi)为像素点p1中的第i个邻域值;Ip1(gc),Ip2(gc)分别是像素p1,p2的中心邻域值;Dp1i,Dp2i分别为p1,p2与中心像素gc的像素差值。
通过式(20)计算得到的Dp1i,Dp2i,再对二者进行对比,输出相邻像素的量化差值
(21)
为了与式(19)对应,需对式(21)进行分解
(22)
最后,基于式(18),对s1(p1i×p2i),s2(p1i×p2i) 进行编码
(23)
通过组合式(23)的F1(p1i×p2),F2(p1×p2), 输出过渡LBP算子LBP(p1×p2)。
最后,将空间内在关系嵌入到LBP(p1×p2) 中,获取邻域空间LBP算子。为了充分利用相邻区域的空间结构特性,本文考虑图像中2个相邻的像素区域,其模式如图5所示
P(r,Δ)=[LBP(c),LBP(c+Δ)]
(24)
式中:Δ为2个LBP中心像素点的距离;r为LBP的半径;c是左侧LBP中心位置。
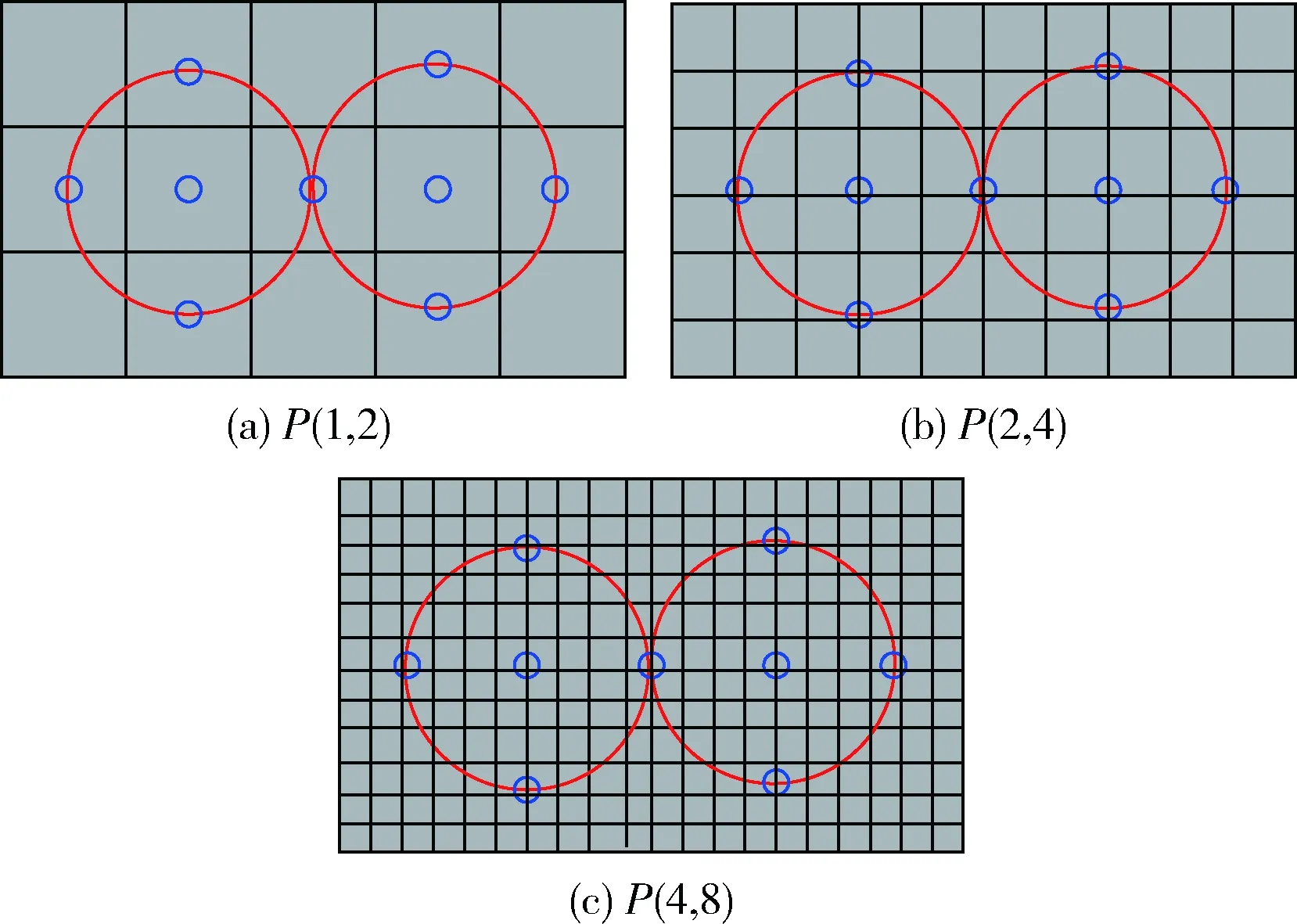
图5 不同(r,Δ)下的P(r,Δ)
再利用式(24)的邻域空间LBP算子对位图BM完成编码后,输出特征矩阵F′,充分提取位图BM的鲁棒特征,增强哈希序列的安全性。将图6(a)作为样本,基于邻域空间LBP模式,提取的LBP特征图像,如图6(b)所示。根据测试结果可知,图像的鲁棒特征被充分检测出来,消除了背景等伪特征。

图6 图像的鲁棒特征提取
2.3 基于主成分分析的紧凑哈希生成与认证
为了获取紧凑的哈希序列,需要将低、高重构电平矩阵L,H,以及特征矩阵F′进行压缩。首先,将L,H分割为非重叠子块,每个子块的尺寸为k3×k3。再计算L,H中每个子块的均值,则对于L,H,均能输出(M/k2/k3)2个像素均值。并将这些均值进行升序排列,将其转换为1D矢量
L={l1,l2,…l(M/k2/k3)2}
(25)
H={h1,h2,…h(M/k2/k3)2}
(26)
其中,li,hi——L,H中第i个像素均值。
随后,通过设置阈值t,对式(25)、式(26)进行量化
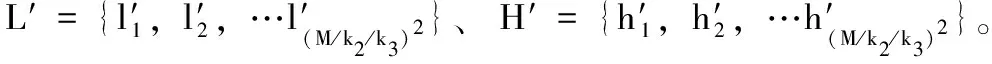
接下来,引入主成分分析[14],对特征矩阵F′进行压缩量化。首先,将尺寸为M×M的特征矩阵F′重构为M/8×8M的新型特征矩阵R,其每一列均含有M/8个元素,并将其表征为R={r1,i,r2,i,…rM/8,i}T,i=1,2…8M, 然后,再利用主成分分析处理,R={r1,i,r2,i,…rM/8,i}T。 依据R={r1,i,r2,i,…rM/8,i}T, 计算其协方差矩阵CR为
(27)
随后,根据式(27)计算得到的协方差矩阵CR,对其进行分解
CR=Γ×Λ×Γ-1
(28)
式中:Λ代表包含CR的8M个特征值 (λ1,λ2,…λ8M)的对角矩阵;Γ为CR的特征矢量。令Γ={Γ1,Γ2,…Γ8M}, 且Γi={ρ1,i,ρ2,i,…ρ8M,i}。 从Γ={Γ1,Γ2,…Γ8M} 中择取前N个特征值,构成新的特征矢量Γ′={Γ1,Γ2,…ΓN},其尺寸为8M×N,则联合大小为M/8×8M的特征矩阵F′,基于主成分分析原则,可获取M/8×N的新矩阵Γ″
Γ″=F′×Γ′
(29)
式中:Γ″包含了图像的主成分,充分反映了矩阵F的主要特征中的各要素间的相关性。最后,把新矩阵Γ″划分为一系列的非重叠子块,每个子块的大小为k4×k4。在Γ″中,每个子块的像素均值mj均与Γ″的均值mΓ进行比较,完成对特征矩阵F′的压缩量化,输出二值序列r′
(30)
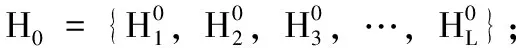
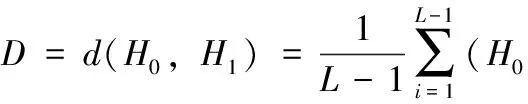
(31)
式中:L是哈希长度;⊕是异或运算。
由式(31),当D值小于用户阈值W时,将可疑图像视为完好图像;反之,将其判别为篡改图像。
3 实验结果与分析
为了测试所提图像哈希算法的鲁棒性,在UCID数据库[16]中完成实验,且将为文献[6]、文献[7]视为对照组,以体现所提哈希技术的优异性。由于本文算法包含了图像预处理、鲁棒特征提取,以及紧凑哈希生成与认证3个模块、因此,根据每个部分的功能,按照模块化设计,对每个过程进行编程。因此,本次实验是基于Matlab 2010平台,其具有强大的数值计算、数据分析与图像显示等功能[15],同时,借助VC++6.0语言进行算法编程与实现。且实验环境为:window7,64 bit专业版的操作系统,CPU为Intel(R) Core(TM)i5-457、主频为3.20 GHz,内存为4.0 GB,且硬盘为500 G。
并采用ROC曲线[6]中对3种哈希技术的鲁棒性进行量化,由正确识别率PTPR、虚警率PFPR构成
(32)
式中:n1为正确判断图像数量;n2是误判图像数量。M1、M2分别是完好图像与可疑图像的总数。
根据本文哈希算法的描述过程可知,阈值W对整个哈希序列的鲁棒性影响较大。故首先需对W值完成优化。关键实验参数为:r=2,Δ=4。其余参数见表1。
3.1 用户阈值W的优化
为了对阈值W进行优化,利用最佳的阈值进行了哈希认证,本文借助UCID图像库[16],从中选用800幅图像作为本实验的测试目标,同时,按照表2的攻击类型赋予所有图像。

表1 实验参数
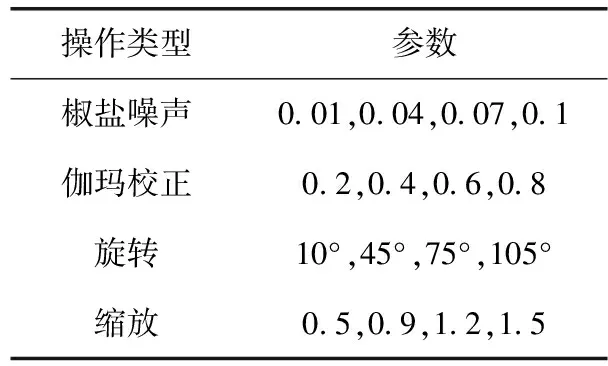
表2 不同类型的内容攻击
图7为图像对应的Hamming距离与其频数分布状况。由频数分布可知,对于视觉相似图像,在其Hamming距离D<0.43时,对应的频数分布变化较为强烈;而对于视觉差异图像对,在其Hamming距离D>0.43时,频数分布较大。所以,根据频数分布费临界值,在所提哈希算法中,将阈值W设置为0.43。
3.2 哈希算法的鲁棒性测试
鲁棒性评估哈希算法的重要指标[6],故在UCID库选取4幅图像作为实验目标,如图8(a)~图8(d)所示;再根据表2的篡改手段对图8(a)~图8(d)完成处理;根据式(31)计算其Hamming距离D,输出数据曲线如图8(e)~图8(h)所示。由Hamming距离可知,在初始图像遇到表2中的篡改攻击后,本文哈希算法所获取的D值都要低于0.43。主要是本文哈希算法通过结合插值、低通滤波以及SVD技术完获取鲁棒性较高的二次图像,有效提高了哈希序列对噪声、缩放以及旋转等攻击的稳健性,并设计了描述能力较强的邻域空间LBP算子,充分提取图像的鲁棒特征,从而提高了哈希序列的鲁棒性。
3.3 抗碰撞性能测试分析
哈希算法的碰撞性能也称为唯一性[1],即两幅感知不同的图像产生相同的哈希序列的概率非常小,两幅感知不同图像对应的哈希序列之间的Hamming距离应该大于阈值。利用本文算法可以生成UCID库的1338幅图像对应的1338个哈希序列,且计算了894 453个不同图像对之间的Hamming距离。再根据碰撞概率计算函数[17],获取3种算法的碰撞概率,见表3。碰撞概率模型为[17]

图7 阈值的优化测试结果
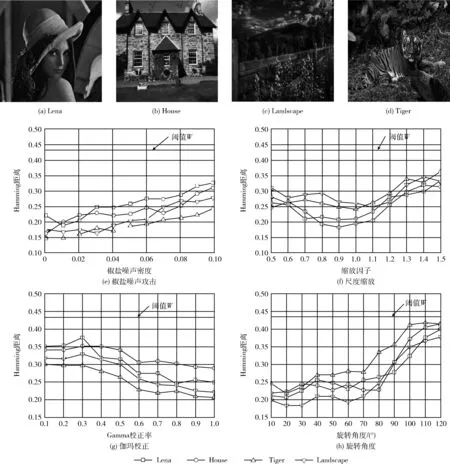
图8 本文哈希算法的鲁棒性测试
(33)
式中:erfc()为互补误差函数;T为阈值;u,σ分别是Hamming距离对应的频数分布的均指与方差,在本文中,通过多次实验,取u=0.456,σ=0.048时,所提算法的Hamming距离呈现一致分布状态。
表3显示了3种算法的抗碰撞性能。由表可知,随着阈值的增加,其碰撞概率也在增大;但是,本文哈希算法的发生碰撞的概率是最小的,远低于文献[6]、文献[7]算法。

表3 3种算法的抗碰撞性能测试结果
3.4 不同算法的鲁棒性测试
再次从UCID库[16]中选取1000幅图像作为实验目标,利用本文算法、文献[6]与文献[7]对其进行处理,生成相应的ROC曲线如图9所示。根据测试曲线,对表2中的4种内容篡改方式,本文哈希算法的ROC特性较为理想,特别是识别旋转篡改,在PFPR=0.2时,所提哈希技术对应的PTPR=0.983。而文献[6]、文献[7]的鲁棒性都要弱于本文哈希算法,其中,文献[7]对旋转篡改的识别能力最低,文献[6]的鲁棒性虽然要优于文献[7],但是仍然弱于本文技术,在PFPR=0.2时,二者的PTPR分别为0.861、0.925。主要是因为本文哈希技术与文献[6]都利用了相应的预处理方法来获取抗旋转的二次图像,但是文献[6]是利用中心对称LBP算子来描述图像特征,忽略了图像的内部空间关系,导致其对鲁棒特性的描述能力不足,而本文算法在经典的LBP算子基础上,考虑图像的内部空间关系以及相邻像素与中心像素之间的灰度差异,设计了邻域空间LBP算子,增强其描述能力,能够充分提取抗旋转的鲁棒特征,使其具有更强的感知鲁棒性,要优于文献[6]。而文献[7]主要是颜色矢量角度与Canny检测算子来生成哈希序列,普通的Canny检测算子在遇到旋转等集合攻击时,其稳定不佳,难以提取图像的鲁棒特征,导致其算法的鲁棒性要低于本文算法与文献[6]。
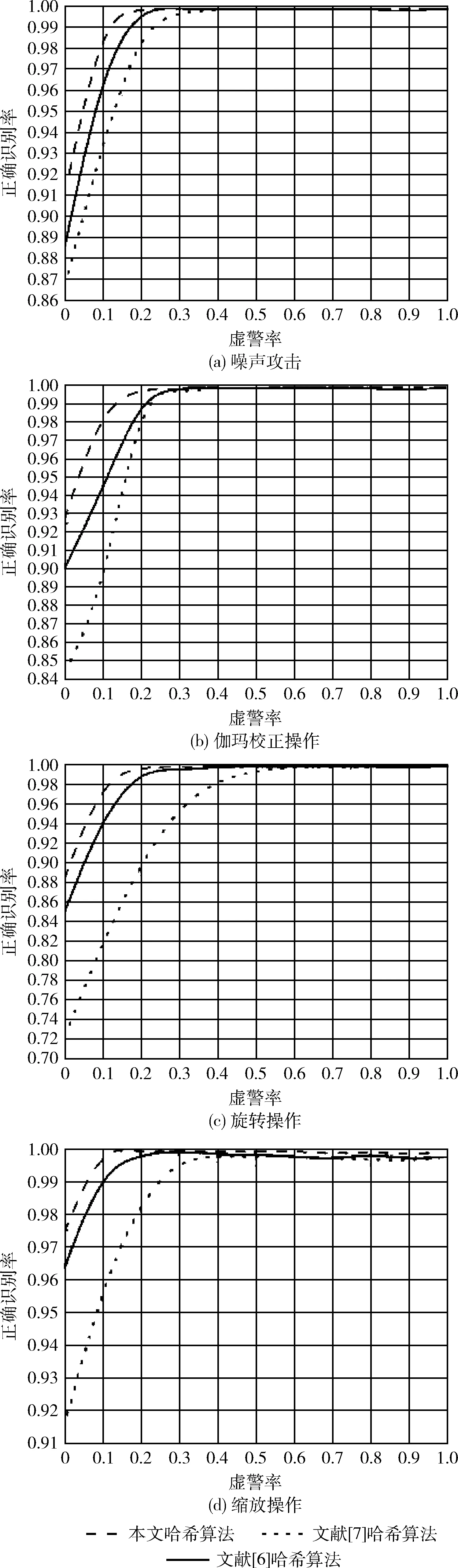
图9 3种算法的ROC曲线测试
4 结束语
为了获取紧凑哈希序列,并改善哈希算法的鲁棒性,本文通过设计邻域空间LBP算子,并联合块截断编码机制,设计了一种鲁棒紧凑哈希技术。通过综合引入线性插值、Gaussian低通滤与奇异值分解,形成图像预处理方法,将输入图像转变为鲁棒的二次图像,增强哈希算法对缩放、噪声以及旋转的鲁棒性;通过块截断编码机制来获取二次图像的高、低电平矩阵,以及二进制位图。考虑图像像素内在的空间关系,设计邻域空间LBP算子,增强对特征的描述能力,提取位图的鲁棒特征。利用量化函数与主成分分析,对高、低电平矩阵,以及特征矩阵进行压缩量化,获取3个二值序列。通过组合3个二值序列,生成图像哈希。实验测试数据验证了所提哈希算法的合理性与优异性。
