基于遗传算法和神经网络的PID参数自整定

王晓天, 边思宇

(1. 大连东软信息学院 计算机科学与技术系, 辽宁 大连 116023； 2. 吉林大学 植物科学学院, 长春 130062)

PID(比例-积分-微分)控制器在过程控制和工业自动化中应用广泛, PID的控制效果依赖于3个参数的设定. 在传统控制过程中, PID参数整定使用经验凑试法, 为了达到预期的控制效果, 逐步调整比例、积分、微分3个系数, 该方法易理解, 但也存在弊端. 首先, 在一些控制系统中, 3个参数KP,KI,KD很难调节； 其次, 传统PID控制器通常在非线性系统、时滞系统和复杂模糊系统中的工作效果较差[1-5]. 提升PID控制效果的关键是能准确且快速地调整参数, 即在控制规律确定为PID形式的情况下, 通过调整3个参数, 使得由被控对象、PID控制器等形成一个闭合回路, 并使其特性达到期望的标准[6-8]. 目前, 已有许多相应的智能参数整定算法. 如扩展Z-N阶跃响应法[9], 其可从脉冲或阶跃响应中直接获取一些简单的过程模型参数, 在加权误差平方积分最小的条件下, 即能从模型参数中得到PID控制器的参数; Astrom等[10]提出了一种继电反馈法, 该方法能快速获得过程临界信息, 由于一般的过程会在有限的周期内振荡, 所以可用振动幅度和振动频率确定临界增益和周期. 但在进行上述参数自整定方法运算过程中, 需要确定的被控对象传递函数仿真, 或直接使真正的被控对象参与其中, 过程繁琐, 不易实现. 本文采用遗传算法, 其中染色体设为PID控制参数, 在进化过程中不断优化参数以达到预期的目标, 并用训练好的神经网络代替被控对象加速运算过程. 最后通过仿真实验验证了所提算法的准确性.

1 PID控制器设计

PID控制器的运行方式为循环工作且线性调控, 在每轮迭代中, 先获得系统输出y(t)与给定值r(t)的差值e(t), 然后分别对其进行比例、微分、积分运算, 将线性组合得到的控制量u(t)输入到被控对象中, 获得的输出量y(t)继续进行闭环工作.u(t)的控制规律为

(1)

本文使用式(1)的离散形式[11]:

(2)

被控对象为一个二阶慢变的仿真温控系统, 控制从0～37 ℃的升温过程. 比例系数KP对输出误差产生成比例的控制作用, 比例大小反映了控制速率的快慢； 微分系数KD主要体现偏差变化率; 积分系数KI的作用则是消除稳态偏差, 可抵消系统的滞后性. 微分和积分都是微调部分, 不宜过大, 否则会产生超调[12].

经过参数整定后, 可得到较好的控制性能, 不同被控对象其参数设定也不同, 且如果被控对象的特性有变动, 则控制器参数也需重新整定. 本文结合神经网络和遗传算法, 在不影响系统正常运行的前提下调整参数, 并把新的参数作用于PID控制器. PID参数自整定的结构如图1所示. 图1中实线区块是PID闭环控制过程, 虚线区块是控制参数调整过程. 由图1可见, 在每个中断时刻, 神经网络先获取被控对象的输入和输出, 再对它们进行训练, 如果发现训练结果的变动较大, 则表明目前的控制器参数适应度降低, 需重新调整参数, 此时会关掉神经网络的训练功能, 而使用遗传神经算法介入参数整定过程, 计算出新的控制参数, 输入控制器中进行更新替换.

图1 PID参数自整定结构Fig.1 Structure of PID parameters self-tuning

2 被控对象的神经网络辨识

被控对象为神经网络提供一组有效的训练数据, 神经网络对其进行训练后用于模拟被控对象. 神经网络的组成单元是许多个神经元, 每个神经元之间的连接强度由权值体现, 多个简单神经元的相互连接即组成了复杂的神经网络. 由于神经元类型、神经元学习方式和连接方式的多样性, 因此神经网络的种类也很多[13]. 本文采用的神经网络算法是误差反向传播算法, 简称BP算法.

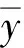
输出层为一个神经元, 对应y. 但隐含层的层数与各层神经元数的确定较难.

本文的被控对象仿真一个二阶慢变嵌入式系统, 隐含层只需3个神经元, 即可达到训练效果. 如果要仿真一个高阶系统、欠驱动系统或含非线性特性的系统等, 则隐含层就需尝试用更多的神经元, 形成更复杂的神经网络[14]. 本文确定的BP算法网络结构如图2所示, 其中:w1,w2,w3,w4,w5,w6分别表示输入层和隐含层之间的权值;w7,w8,w9分别表示隐含层和输出层之间的权值.

图2 BP神经网络结构Fig.2 Structure of BP neural network

BP算法使用梯度下降策略, 基于最小二乘法, 使网络的输出值与期望值的均方误差最小. 在误差达到阈值前, 网络不断迭代, 每次迭代包括信息的正向传播和误差的反向传播. 将一组u,e,y作为一个训练样本, 采集多个训练样本进行神经网络学习. 在学习前, 先对网络权值进行初始化, 输入的数据依次经过输入层、隐含层和输出层的运算处理后, 与给定期望值对比, 得出均方误差, 如果该误差不符合期望值, 则进入误差反向传播阶段, 经过每层去调整神经元间的权值, 使误差的代价函数沿负梯度方向下降. 如此反复迭代, 直到误差小于阈值或训练次数达到上限, 训练完成后把当前的权值作为网络的最终权值, 该神经网络可模拟被控对象.

当PID参数需要调整时, 神经网络用于替代被控对象, 辅助遗传算法进行参数整定. 调整参数后, 神经网络则不断地从被控对象读取测量数据进行训练, 以实时检测被控对象的特性是否发生改变, 判断是否需要重新调整PID参数. 本文PID控制器的目标是使被控对象能保持37 ℃左右, 只要赋予合适的参数, 即可达到控制目标, 此时系统是稳定的. 但如果被控对象变化或产生一些外部因素, 原始的参数即达不到控制目标, 系统变得不稳定, 需要重新调整参数.

图3 系统稳定(A)和不稳定(B)时的训练结果比较Fig.3 Comparison of training results in stable system (A) and unstable system (B)

因为隐含层中的神经元数量较少, 训练数据太多将出现欠拟合现象. 因此数据的选取应适量, 本文选取300个训练数据. 图3为系统稳定和不稳定时神经网络的训练效果, 单位采样时间为1 s, 为清晰展现数据的训练效果, 图3间隔标出部分测量数据的采样值. 由图3可见, 无论系统处于哪种状态, 神经网络都可对被控对象进行训练. 此外, 选取的训练数据含有高斯噪声, 由训练结果可见, 神经网络在数据拟合方面具有滤波功能.

3 遗传神经算法整定PID参数

本文把训练完成的神经网络嵌入到遗传算法中, 协助优化PID参数. 算法的基本思想： 生成初始种群, 计算每个个体的适应度, 并对当前的种群进行选择、交叉和变异操作, 其中每项操作都基于相应的概率, 根据每个个体的适应度大小决定个体进入下一代的概率, 然后得到新的种群, 继续计算适应度函数, 继续迭代进化过程, 直到种群适应度达到预期标准为止. 由于下一代的种群继承了父代种群的一些优良特征, 所以整体的种群进化方向趋向最优解[15].

种群的数量被控制在20～100较好, 虽然种群数量越大越有可能得到最优解, 但运算时间也越长. 染色体使用实数编码, 由KP,KI,KD三个参数组成. 为确保收敛, 各控制参数的取值范围应谨慎选择. 变异和交叉都在各自的概率下有序进行. 最终用适应度函数评判个体是否优秀的标准, 根据适应度大小对种群进行筛选, 筛选方式可用比例选择法、排序选择法、轮盘赌选择法和竞争式选择法[16]. 本文采用比例选择法.

(3)

由式(3)可见, 染色体适应度的运算过程需得到系统运行中被控对象多个采样点的e(t)和u(t), 并且遗传算法的进化过程需要计算多代种群的适应度, 因此整定算法对于系统的运行成本巨大. 而神经网络已训练好, 可用于对被控对象进行辨识, 所以, 神经网络可代替被控对象在系统中运行, 参数整定全过程可实现离线操作. 遗传神经算法的流程如图4所示. 图4中上半部分是神经网络辨识部分, 下半部分是遗传算法, 只有在需要调整参数时才会进入下半部分的运算. 首先, 染色体种群是随机生成的, 在后续调整中, 种群围绕当前的系统参数, 在一定范围内随机生成. 其次, 计算种群整体的适应度大小, 并以此为依据对种群进行筛选, 在一定概率下对种群进行交叉操作和变异操作, 得到新一代的种群, 继续计算适应度, 重复迭代, 不断进化, 直到迭代次数达到上限为止.

图4 遗传神经算法流程Fig.4 Flow chart of genetic neural algorithm

在种群进化中, 每次迭代计算种群适应度时, 都会选出一条适应度最大的染色体, 作为当前最优的PID参数. 因此, 控制系统的等待时间最多就是一次迭代的时间, 在两次迭代进程中, 控制系统暂时先用上一次迭代的最优参数, 无需等待下一次的结果, 直到下一次迭代结束, 有新的参数传出, 替换当前的参数, 继续迭代过程.

在本文的仿真试验中, 进化结果选取适应度最大的染色体作为最优PID参数, 用于控制被控对象, 使温度调节到稳定值37 ℃. 下面将基于遗传算法和神经网络的整定方法简记为GA-NN法, 并将其与传统凑试法进行对比, 结果如图5所示. 由图5可见, GA-NN法的震荡幅度比凑试法小, 且达到稳定所需时间更短.

图6为GA-NN法和凑试法得出的PID控制曲线与期望值的误差曲线对比. 由图6可见, GA-NN法的误差比凑试法更小, 收敛速度更快.

图5 PID控制阶跃响应曲线的对比Fig.5 Comparison of step response curves by PID control

图6 PID控制误差的对比Fig.6 Comparison of PID control error

为更精确地展现这种差别, 下面从超调量、上升时间和ISE(平方误差积分)三方面对GA-NN和凑试法的性能进行比较. 其中: 超调量反映了输出值偏离稳定值的程度; 上升时间反映了控制过程趋于稳定所需的时间; ISE反映了控制过程整体的稳定性. 对比结果列于表1. PID的3个参数对比列于表2.

表1 PID控制性能对比

表2 PID参数对比

由表1可见, 本文算法在超调量、上升时间和ISE方面均较传统凑试法有所改善, 可提高近50%的性能. 因凑试法受人为因素影响较大, 本文仅针对凑试法的平均水平进行比较.

综上所述, 本文提出了一种智能PID参数整定算法, 基于传统控制系统的经验凑试法, 采用遗传算法对PID控制系统的参数进行优化, 替代人工调参, 提高了参数整定的效率. 引入神经网络训练方法替代被控对象, 使参数整定的过程可离线操作, 不用受制于被控对象, 加快了参数整定速度. 通过仿真实验对比, 验证了本文算法的鲁棒性和有效性. 但本文算法应用于高阶系统时效果欠佳.