赋广义Orlicz范数Orlicz函数空间的某些特殊可补子空间的存在条件

段丽芬，庄彩彩，高 晶

对于赋Luxemburg范数和Orlicz范数的Orlicz函数空间中存在与l∞，c0，l1几乎等距同构的可补子空间的条件均已获得［1-2］，本文根据广义Orlicz范数的特征，给出了赋广义Orlicz范数Orlicz函数空间中存在与l∞，c0，l1几乎等距同构的可补子空间的条件.

1 预备知识

定义1［3］设 M 是Banach空间 X 的闭子

定义2［2］设 X 和Y 是Banach空间，如果对任给ε＞0，X中都存在与Y同构的可补子空间X0，使得其同构映射T满足1+ε，则称Y与X的可补子空间X0几乎等距同构.

定义3［2］若偶函数M是非负连续凸函数，且u=0⇔M(u)=0，则称映射 M:R→[0,∞)为Orlicz函数.称满足的Orlicz函数为N-函数.

设(G,Σ,μ)为一无原子测度空间，L0表示定义在G上的所有可测实函数构成的集合.对任意 x∈L0，定义 ρM(x)=∫GM(x(t))dt为 x(t)关于M的模.

M∈Δ2指如存在常数 k≥2和 x0＞0，当时 ，满 足 M(2x)≤kM(x).M∈∇2⇔N∈Δ2.

2 几个引理

引理1［2］（詹森不等式）设 M 是 N 一函数，x∈L*M，且ρM(x)＜∞，则

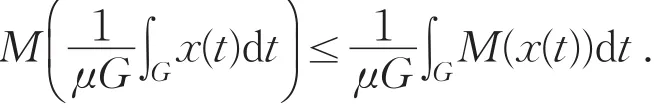
引理2 设M是N一函数，M∉Δ2，则对任给 ε∈(0,1)，都存在 xn=unχGn∈L*M，其中un＞0, μGn＞0,Gi⋂Gj=Φ(i≠j),n=1,2,… ，使得，且对任何1＜p＜∞，都有

证明 i）因 M∉Δ2，存在 un＞0,un↑∞ 及具有正测度两两互不相交的子集列{Gn}，使得

记 xn=unχGn，则

3 主要结果

定理1 设M是N一函数，M∉Δ2，则对任何1＜p＜∞，有

i）LM,p中都存在与l∞几乎等距同构的可补子空间.

ii）EM,p中都存在与c0几乎等距同构的可补子空间.

证明 i）设ε∈(0,1)，xn与引理2中所取相同，定义，及T:l∞→X,使得显然 T是同构映射，且由引理2之ii）知.下面证明 X是 LM,p中的可补子空间.

事实上，定义 P:LM,p→LM,p，使得

显然P是线性算子，且P2=P.现只需证明P是有界的且PLM,p=X即可.

因为对任意k＞0及 x∈LM,p，利用引理1得

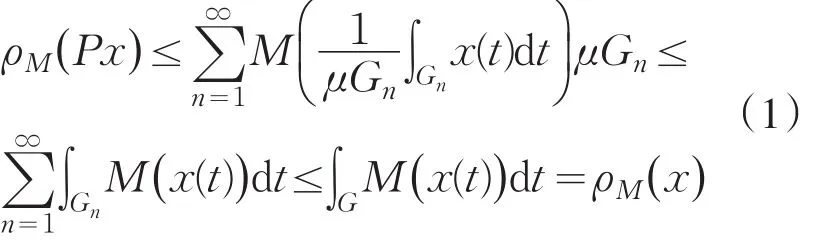
现证明PLM,p=X.因对任何 x∈X，都有Px=x ，说明 PLM,p⊃X.另一方面，设则 P(x)=.故

ii）将上面i）证明过程中的 X换成 X0=，则 X⊂E.相应T 定0M,p义为T:c0→X0,使得显然T同样是同构映射，1+2ε.在证明X0是EM,p中的可补子空间时，只要注意到，则由不等式（1）可得从 而

定理2 设M是N一函数，则对任何1＜p＜∞，下列命题等价：

i）M∉∇2.

ii）LM,p中都存在与l∞几乎等距同构的可补子空间.

iii）EM,p中都存在与c0几乎等距同构的可补子空间.

证明 根据定理1，只需证明iii）⇒ i）即可.由iii）可知，LM,p中存在子空间与c0拓扑同构，利用范数的等价性，LM存在子空间与c0拓扑同构，结合文献［1］定理1.90立即可得结论.

定理3 设M是N一函数，M∉∇2，则对任何1＜p＜∞，LM,p和EM,p中都存在与l1几乎等距同构的可补子空间.

证明 设 ε∈(0,1)，利用引理 2，存在yn=vnχGn∈L*N，其中 vn＞0,μGn＞0,Gi⋂Gj=ϕ(i≠j),n=1,2,…，使得，且对任何1＜p＜∞，都有.因 yn∈EN,q，利用引理3，存在xn=unχGn(un＞0)，使得＜xn,yn＞ =unvnμGn.置则对任意，都有.利用文献［4］中引理2立即可得，x∈EM.这说明X⊂EM.

定义T:l1→X,使得.显然T是同构映射，且，即‖T‖≤1.另一方面，

事实上，定义P:LM,p→LM,p，使得 P(x)=

定理1中已经证明P是有界线性算子，且P2=P，PEM,p⊃X，现只需证明PLM,p⊂X即可.

定理4 设M是N一函数，则对任何1＜p＜∞，下列命题等价：

i）M∉∇2.

ii）LM,p中都存在与l1几乎等距同构的可补子空间.

iii）EM,p中都存在与l1几乎等距同构的可补子空间.

证明 结合定理3，只需证明ii）⇒i）即可.因为LM,p中存在与l1同构的可补子空间的充要条件是其共轭空间L′M,p=LN,q⊕F中存在与c0同构的可补子空间.利用定理1可知，当M∈∇2，即N∈Δ2时，LN,q中不存在与c0同构的可补子空间，结合文献［1］中引理4和定理5，结论得证.