微分与积分概念的非标准陈述

高婷婷，张明会

随着数理逻辑的发展，特别是元数学、证明论、模型论的异军突起，用数理逻辑的方法研究数学基础问题取得了前所未有的进展，一大批数理逻辑学家投身于不用极限方法，而是改用数理逻辑方法建立分析学的奠基工作，他们利用数理逻辑的方法，重新研究了牛顿-莱布尼茨方法中引进的无穷小元素，特别是本世纪60年代的美国数学家鲁滨逊，从建立在实数系R上的数学命题出发［1］，应用本世纪40年代在严格逻辑基础上建立的紧致性定理：“对形式语言中的任何一个公式集或者命题集A，若A得任何一个有穷子集A′皆有模型，则A必有模型”来研究无穷小量，对无穷小量的存在用数学方法给出了严格的证明，将标准实数域R扩充为包含有“无限小”和“无限大”元素的非标准实数域R*，然后在R*上重新展开微积分的讨论，建立其全部数学分析理论，人们称之为非标准分析.

借助于数理逻辑形式语言可以严格地建立“转换原理”，其结论是：在一阶语言的框架内所表达的数学分析性质，在R和R*内是同真同假的.具体地说，就是当形式语言中两次的变化范围仅限于实数时，可以形式地把R和R*上的陈述互相转换而不改变其真假性.

1 导数与微分

给定标准实值函数 f:R→R，取定一点x0∈R ，在 R*上讨论，令 ε为非零无限小［2］.如果式的标准部分存在且为一有限函数.即，则称 f(x)在x0点可微，有限数 f′(x0)就叫 f(x)在 x0点的导数.

上述定义是构造性的，即只要对此式让无限小元素参与通常数的计算，如果运算结果的标准部分存在，就得出 f在x0点的导数，从形式上说这一定义完全与牛顿的流数术相同.但是其运算过程是建立在无限小元素存在的严密逻辑基础上的，不会出现悖论.显然有下述命题.

命题1 标准实值函数 f(x)在x0∈R有导数的充要条件是

例1 设 f(x)=x2+3x ，求 f′(x).

微分的定义如下：记Δy=f(x+Δx)-f(x)为相应于该变量Δx的函数y=f(x)的该变量，称dy=f′(x)Δx为函数 f(x)在 x点处对应与Δx的微分，dx=Δx为自变量 x的微分［2］，当dx≠0时，则，但是，即f′(x) 是无限小，可得 Δy=f′(x)Δx+ εΔx ，即Δy=dy+εΔx.

定理1 设 y=f(x)，对于 x∈R ，f′(x)存在，且Δx为无限小，则Δy和dy都是无限小，而且Δy=dy+εΔx.其中，ε为依赖于 x和Δx的无限小.

2 积分的非标准陈述

2.1 等和原理

等和原理是标准分析中的杜哈美原理在非标准分析里的拓广，在处理无限小求和问题中非常有用［3］.为了下面的应用仅列出其内容如下.

设在∗R上有两个正无限小数列其各对应项间满θω=l（有 限 数），又 设 { r1,r2,⋅⋅⋅,rω}和是两个有界数列，各项之间有关系，那么有成 立［4］，即，特 别 地 ，当时，上述关系式亦成立，下面在积分概念的应用中就使用此特殊情形.

2.2 积分概念的陈述

为了能抓住问题的主要方面，显示出非标准分析在处理诸如积分这类问题时的特色，即用“有限结构”来逼近标准无限结构，下面仅以连续函数为例引入积分概念.

设给定一连续函数 f:[a ,b]→R，我们在∗R上来考虑问题.任意取区间[a,b]的无限小划分，其 中 ，并且 Δxj=(xj-xj-1)≃ 0(j=1,2,…,ω).在任意选定ξ={ξj}满足则是唯一确定的，即它和区间的无限小划分Δω及点ξj的选取方式无关，这个唯一确定的数值，就定义为 f在[a,b]上的定积分［5］，即

上述积分存在的唯一性可以用等和原理证明（参见徐利治等著《现代无穷小分析导引》）.我们应特别注意这种“实无限小分划结构”的数学模式，为描述自然界中的连续性，提供了一个新的突变式的手段.不需要像标准分析中那样，在那里积分定义是通过有限积分和就所控制的极限过程而完成的.

2.3 积分基本定理

牛顿-莱布尼茨公式［6］：设 F(x)是 f(x)的一个原函数，即F′(x)=f(x)(a≤x≤b)，则F(b)-F(a).

证明 因为积分值是唯一确定的，可以取一个等距的无限小分划方式Δω，其中xj=a+(j/ω)(b-a)(j=1,2,⋅⋅⋅,ω).记 xj-xj-1=(b-a)/ω=dx，于是，根据导数的定义并借助于等和原理［7］，便得到

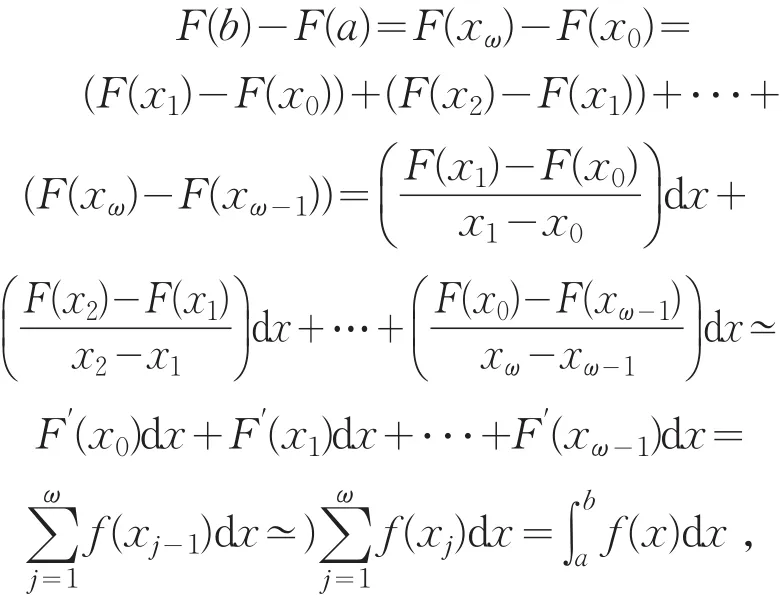
3 结论

微分和积分的非标准陈述研究，一方面，让教师在讲授中能掌握其要领，在教学中融会贯通，使学生在学习中能正确领会，尤其把握借助于微分和积分两个概念的非标准陈述，利用熟知的例题和定理加以证明讨论，把微分和积分概念进行了全新阐述和解释，对教学更有促进；另一方面，作为研究的一个新途径，通过研究开辟新的领域，使之与教学相长、以研促教、以教促改.