在游戏中经历“反算”
2018-07-16郜舒竹
郜舒竹
“课堂革命”指向的是学生的“创新精神”和“实践能力”的培养。这是时代对教育提出的要求和挑战。创新精神和实践能力,都不可能在被教状态下养成。因此课堂革命首先需要将以“教师教的活动为主”的课堂教学,改变为“以学生学的活动为主”的课堂教学,也就是要把“教为中心”改变为“学为中心”。这样的改变可以简称为“变教为学”。实施变教为学教学改革,需要教师在行为与技术方面的三个转变:教学需要“变讲解为引发”;管理需要“给自由引自律”;评价需要“视错误为多样”。针对这些难题,本栏目将陆续刊登相关研究。欢迎赐稿。
【摘 要】数学教学改革倡导“变教为学”,实现这种改革的一个技术型难题是为学生设计有效、有趣的学习活动。反算作为人日常工作、科学与数学研究的真实活动,需要让学生在数学学习过程中亲身经历。为了引发学生参与反算活动的兴趣,可以将具有操作性和趣味性的扑克牌游戏融入到学习活动中。
【关键词】反算;课堂革命;学习活动;扑克牌;混合运算
我国小学数学教学历来有所谓概念教学、计算教学等说法,其中的计算教学通常会强调所谓“算法”和“算理”。遵循的模式一般是“给出算式算出结果”“怎样算”的问题叫作算法,“为什么这样算”的问题叫作算理。
依据对立统一方法论的基本观点,对立的双方应当并存,并且在适当的条件下可以相互转化。因此任何过程都应当有与之方向相反的过程存在,针对“给出算式算出结果”的过程,就应当有“知道结果寻找算式”的过程。如果把前者叫作“正算”,那么后者就可以称为“反算”。
一、“反算”是人的真实活动
“反算”一词多用于科学和数学研究领域,对应的英文单词是“Inverse Operation”,其本意是“反过来算”,或者“反过来做”。比如,如果把数“2”和“4”看作两个已知的数,那么就可以对这两个数实施加法运算,表示为“2+4”,对应的结果就是“6”。相对于这样的运算,可以反过来想,还有什么样的数以及运算可以得到结果6?也就是把“6”看作已知的数,去寻找两个数以及相应的运算,其结果可以等于6。经过思考与计算,可以得到如下算式的许多结果:
3+3,10-4,3×2,12÷2
这些思考和计算就成为前面“2+4”计算过程的反算过程。反算是相对于“正算”来说的,如果把从“2+4”得到“6”的过程看作“正算”过程,那么去寻找如何能够算出“6”的过程就成为相对于这个正算的反算过程。
这样的过程与方法在日常工作以及生活中会经常遇到。比如,如果已知飞机的平均时速是每小时700千米,如果飞行1.5小时,可以计算出飞行距离为:
700×1.5=1050(千米)
实际情境中,出差旅行的旅客登机后,最关心的问题往往不是飞行距离,而是“几点到”,也就是飞行时间。因此如果把已知速度和时间求出飞行距离的过程看作正算的过程,那么去寻求飞行时间的过程就是相对于正算的反算过程。
再比如缴纳个人所得税的问题,如果一个人的月工资为4500元,那么应缴纳个人所得税的税率为10%。也就是每月缴纳个人所得税450元,实际获得工资收入为4050元。这样的计算过程是已知月工资总额和税率,求出缴纳税款金额和实际工资收入的过程。在现实中人们遇到的实际问题往往是需要反过来思考的,每月发工资时,首先看到的是实际工资收入,这时自然的问题是想知道“扣了多少税”以及“按照什么税率扣的税”,解决这样问题的过程就成为前面正算的反算过程。
反算不仅是人们日常活动中经常遇到的,同时也是数学与科学学习、研究中的常用方法。比如把指数运算看作正算,那么相应的对数运算就是反算过程;把三角函数看作正算,对应的反三角函数就是反算过程;等等。将反算过程融入到数学学习活动中,让学生亲身经历这样的活动,对于拓展数学学习内容,丰富数学学习经验,开拓学生思维会有所裨益。
二、“24点”游戏与反算
计算在数学学习中通常被认为是枯燥的,如何在计算活动中引发学生的兴趣,是教学研究的重要课题。将具有操作性以及趣味性的游戏融入到计算活动中,对于提高开展学习活动的兴趣自然是有益的。“24点”游戏是利用扑克牌所进行的一种智力游戏。 其规则非常简单,把四张牌上的四个数,用加、减、乘、除算出24,与扑克牌的花色无关。比如用下面四张牌上的数字算出24。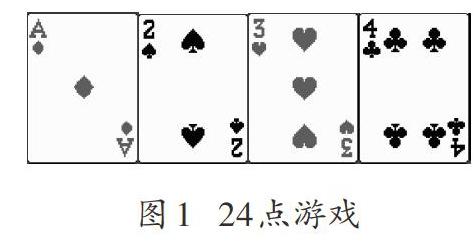
這一问题的思考与解决过程,实质上就是学生通常熟悉的混合运算过程的反算过程,其结果至少可以是如下三种情况:
l 1×2×3×4=24
l (1+2+3)×4=24
l (2+4)×(1+3)=24
反算过程的结果往往具有多样性和不确定性。在实际教学中,充分利用这样的多样性设计学习活动,有益于沟通不同算法之间的联系,开阔学生的思维。
三、游戏中的深入思考
游戏过程中可以引导学生开展“问题生问题”的思考活动。比如在解决了图1“1,2,3,4”的情况后,可以引导学生思考:
l 用四个连续自然数计算24,可以怎样算?
这其中实际上包含了“2,3,4,5”“3,4,5,6”等九个问题。受一个问题的启发,得到了一系列新的与之相似的问题,可以叫作“问题链”。每种情况的答案列举如下:
(1) 2,3,4,5
(5+3-2)×4=24,(5+4+3)×2=24
(2) 3,4,5,6
(5+3-4)×6=24
(3) 4,5,6,7
(7+5-6)×4=24,(7+5)×(6-4)=24
(4) 5,6,7,8
(7+5-8)×6=24,8×6÷(7-5)=24,(8-6)×(7+5)=24
(5) 6,7,8,9
8×6÷(9-7)=24
(6) 7,8,9,10
8×9÷(10-7)=24
(7) 8,9,10,11
经过反复尝试,怎么也算不来。由此有理由猜想,也许满足要求的算法是不存在的。事实上,通过计算机检验,算法的确是不存在的。
(8) 9,10,11,12
(11+9)×12÷10=24,(12+11+10)-9=24
(9) 10,11,12,13
(13+12+10)-11=24
类似的,还可以研究连续奇数、连续偶数、四张相同数等有规律的四张牌。下面研究四张相同数的牌,从最简单的开始:用四张“A”能否算出“24”?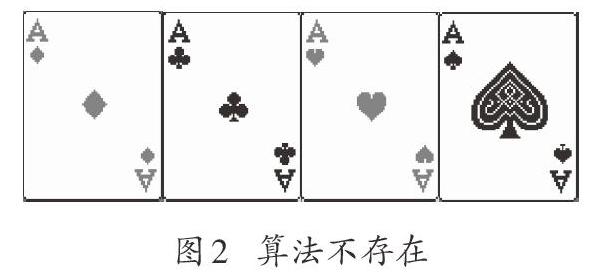
经过反复尝试,怎么也找不到算法。这时,应该思考算不出来的原因,这个原因有两种可能性:一是算法存在,我没找到;二是算法根本不存在。此时思考的目标应该体现在判断哪一种可能性大上。由于经过“反复尝试”也没有找到,因此有理由判断算法不存在的可能性大。有了这样的判断,下面的思路就不再是“找算法”,而是“证明不存在”。
很容易看出这四张牌上的数字运用加、减、乘、除四则运算,能够算出来的最大数是4,因此用四个“1”得出“24”的算法是不存在的。下面再看两个用常规思路不易解决的问题:
l 用下面四张牌算出“24”。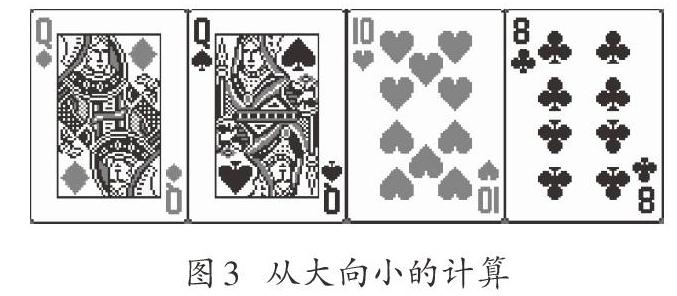
通常人习惯的思路,一般都是“自小而大”,也就是习惯使用加法和乘法。当“自小而大”的思路算不出的时候,千万不要轻易下结论说“算法不存在”,可以想想“自大而小”,也就是减法和除法。
下面的两个算法都是“自大而小”:
(8+12)×12÷10=24,12×10-12×8=24
第二种算法其实就是利用小学二年级就学过的“乘法意义”。10个“12”减去8个“12”等于2个“12”。有些问题的思考还需要用到小数或者分数:
l 用下面四张牌算出“24”。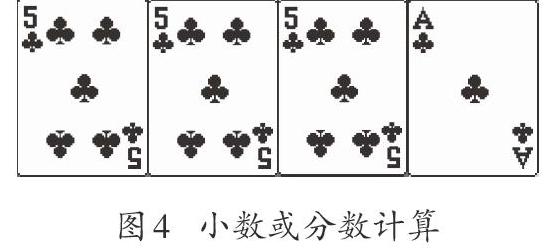
一般習惯的思维方式是“整数的运算”,而不习惯“分数的运算”。这个问题如果用“整数的运算算不出来”,可以想想“分数的运算”。把“5”看作25个“[15]”,可以得到:(5-1÷5)×5=24。
我们通常所说的“聪明”,其实就是在“习惯”的思路受阻的时候,能够运用“不习惯”的思路去思考。
当今的数学教学提倡“变教为学”,也就是将“以教师教的活动为中心”的课堂教学,改变为“以学生学的活动为中心”的课堂教学。这样的教学改革所面对的一个技术型难题,就是为学生的学习设计有效同时有趣的学习活动。突破这样的难题,需要创新的设计,需要实践的检验,需要点滴的积累。
(首都师范大学初等教育学院 100048)
