发挥试题的育人价值 提升学生思维品质

张安军

(浙江省台州市白云中学　318000)

中考试题是命题者集体智慧的结晶，是数学试题库中一笔巨大的精神财富．其中多数中考试题标新立意，既体现了在知识交汇点处命题的创新原则，又格调清新、意境幽深．怎样最大限度地发挥这些试题的育人功能是每位一线教师都在思考和研究的问题．下面笔者就以一道平面几何试题及其变式的解法探究过程为例谈谈这方面的实践与思考，期待与同行交流.

1　试题再现及分析

问题1(2017年台州市中考试题)如图，有一个边长不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组平行的对边上，另外两个顶点B，D在正六边形内部(包括边界)，则正方形边长a的取值范围是．

图1

本题是填空题的压轴题，试题巧妙设计正六边形内部放置一正方形，由于正方形相对的顶点在正六边形一组的对边上可以滑动，为考生营造一个数学探究的环境，要求考生动手操作，对两个几何图形的位置进行几何构图，化动为静，运用合情推理的思想方法，发现问题的内部特征及相应的解决方法，形成相应的结论，重点考查了学生的空间观念和几何直观．

2　在反思、质疑中，培养思维的严谨性

第16题得分点1得分点2分值(分)523平均得分(分)0.980.790.19难度系数0.1960.3950.06

通过上表发现，得分点1、2难度系数分别为0.395、0.06，考生实际得分比预估的还要差．主要原因为图形在动态的过程中，学生缺乏构图能力，对正方形和六边形空间关系缺乏直观想象．《义务教育数学课程标准(2011年版)》指出：“学生的学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动.”因此适当让学生在理解题意的基础上，运用有关工具(如纸张、剪刀、模型、测量工具、作图工具以及计算机等)动手操作，通过自己动手、动脑，用观察、模仿、实验等手段获得经验基础上提出合理的猜想．

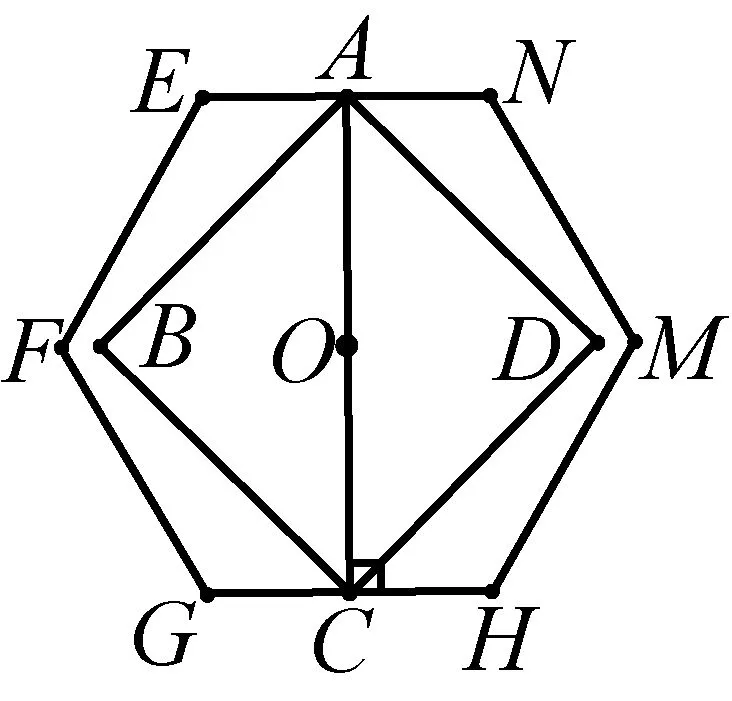
图2

例如，当学生得到图2时，很快得到正方形边长的最小值，教师还要让学生知其所以然，“为什么图2中，正方形ABCD是边长最小？”，“边长最小的正方形ABCD位置唯一确定吗？”

其次，由于画出的图形不是很准确，学生误认为图3的四边形AFCM是正方形，教师追问“为什么四边形AFCM是正方形”或者“线段AO=OF吗？”，在教师追问中，学生意识到问题所在，“马虎构图，缺乏验证”．

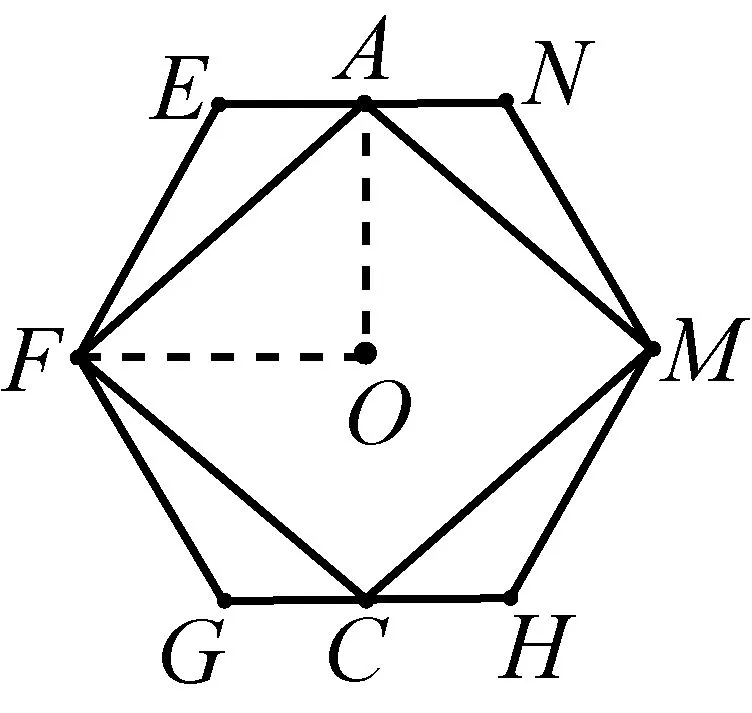
图3

由于受到直观的启发，要使正方形ABCD的边长达到最大，其余的两个顶点都要落在正六边形的边上，于是学生在图3的基础上得到图4时，四边形ABCD是正方形，在计算时默认为AB∥EF，教师追问“为什么AB∥EF？(先要证明△APO≌△BQO，这样才能得到AB∥EF)”，“边长最大的正方形ABCD位置唯一确定吗？(最大的正方形ABCD存在两种位置，另一种当A点在线段PN上时)”

图4

数学探究包含着猜测、错误和常识、证明与反驳、检验与改进等活动，质疑精神在其中发挥了重要作用,在日常教学中教师要有意识地培养学生反思和质疑的意识，运用理性思维验证自己的猜想或他人提出的问题，从而培养学生严谨的思维和理性精神．

3　在一题多解中，培养学生思维的广阔性

思维的广阔性是指对一个数学问题能从多方面考虑，进行多角度的思考．具体表现为对一个数学问题能作多方面的解释，对一个研究对象能用多种方式表达，对一个题目能想出多种不同的解法．一题多解能快速整合所学知识，重要的是能培养学生细致的观察力、丰富的联想力和创造性的思维能力.教师要通过一题多解的分析训练，培养思维的广阔性．

针对上面问题，学生对正方形的最大值不易求得，组织学生开展求正方形边长最大值多解活动，将“还有其他解法吗？”的自我追问变成解题习惯，培养学生思维的发散性.

图5

图6

图7

波利亚指出：“拿一个有意义又不复杂的题目去帮助学生发掘问题的各个方面，使得通过这道题就好象通过一道门户，把学生引入一个完整的领域．”本题所涉及到解直角三角形，方程，正多边形，等腰三角形等有关性质的灵活运用，虽然方法不同，但最后都构建一个直角三角形，把所有的已知量集中到这个直角三角形；这里一题多解是从不同的角度探索解题的思路，有助于学生对平面几何有关知识系统把握，整体建构，同时有助于发散思维的训练与培养．

4　一题多变中，培养思维的灵活性

思维的灵活性是指数学思维能及时地随机应变地应对研究对象的变化，以及尽可能地不受思维定势的影响，而且善于摆脱旧的模式或通常的制约条件．其表现为对知识运用自如，善于变通和调整思路，善于运用辨证思想进行具体问题具体分析．在解题教学活动中不失时机的进行变式教学是培养学生思维灵活性的重要途径．通过一题多变，借题发挥，达到以点带面，举一反三，触类旁通的目的，一方面救学生于题海之中，不让学生感觉到有永远做不完的数学题，培养学生学习数学的兴趣，另一方面提高学生思维的灵活性．

问题2已知正方形ABCD边长为1．

(1)求作等边△PQM，使P、Q、M分别在正方形ABCD各边上．

(2)上述(1)中的等边△PQM是否唯一存在？若不唯一，请求出等边△PQM的最大边长？

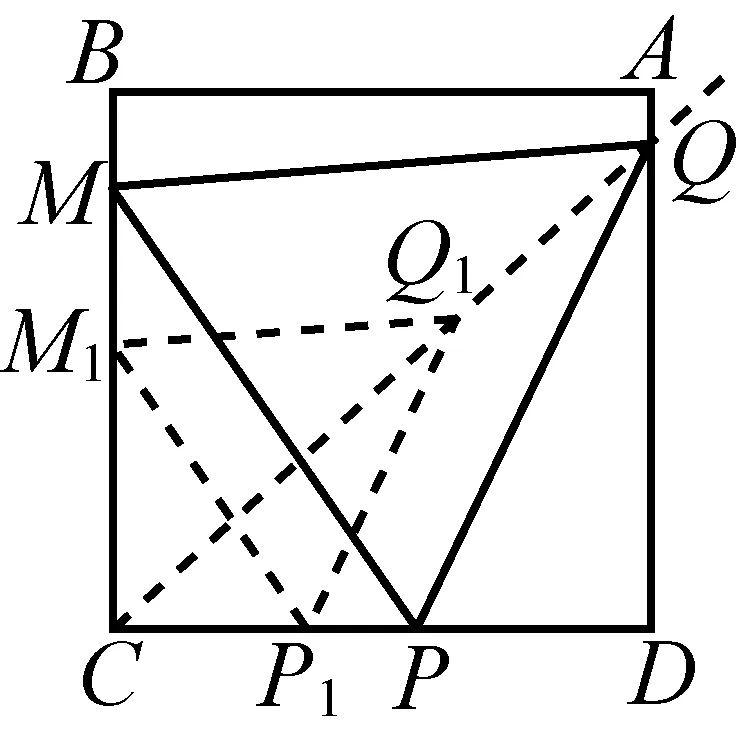
图8

图9

解法2分析：如图10所示，假设存在等边△PQM，M，P，Q分别在BC，AD，AB上，过Q点作QN⊥MP于N点，因为∠MBQ=∠QNM=90°，B，M，N，Q四点共圆，所以∠QMN=∠QBN=60°；同理，∠QPN=∠BAN=60°，△BAN是等边三角形，而N点是定点，这个过程是可逆的，过N点作一条直线分别于BC，AD交于点M，P，再过N点作MP的垂线交AB于Q，则△PQM就是等边三角形；其中M(P)点与C(D)点重合时，△PQM的边长最大.

图10

波利亚曾形象地指出：“好问题同某种蘑菇有些相象，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个．”在上述中，通过减少正多边形的边数，学会采“蘑菇”，学会推广，善于引导学生对一个好问题进行变式改造，如改变题目的条件、结论、图形、叙述方式等使学生跳出自己思维的框架，增加思维的灵活性.

5　再变化问题，培养学生思维的深刻性

思维的深刻性是指学生对数学问题的理解与思考的深入程度，是创造性思维的基础. 反映了学习者善于透过数量关系和空间形式等现象和外部联系，揭示出数学问题的本质和规律的思维品质. 深刻性是思维品质的基础，只有深刻地理解知识，深入地思考问题，才能系统化和一般化地解决问题.对于上述问题，教师可以通过引导学生进一步改变问题，如将原有问题中的背景正方形在正六边形的内部变成正方形在正六边形的外部，又如减少正多边形的边数等，从而促进学生发现问题的本质，优化学生的知识结构，提高学生灵活解决问题的能力，从而避免了反复的机械训练.

问题3如图11，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内(包括正方形的边)．当这个正六边形的边长最大时，AE的最小值为 ．

图11

问题4已知等边三角形ABC.

(1)求作一正方形EFGH，使正方形EFGH各顶点落在△ABC的各边上；

(2)若等边三角形ABC的边长为1，则正方形EFGH边长为多少？

问题5已知直角三角形ABC，∠C==90°，BC=a，AC=b，AB=c．

(1)求作一正方形EFGH，使正方形EFGH各顶点落在直角三角形ABC的各边上；

(2)上述(1)存在最大正方形EFGH吗？若存在，则最大边长为多少？

问题6已知锐角三角形ABC，BC=a，AC=b，AB=c．

(1)求作一正方形EFGH，使正方形EFGH各顶点落在三角形ABC的各边上；

(2)若a≤b≤c，上述(1)中存在最大边长正方形吗？若存在，则最大边长为多少？

思考和分析：如果减少正多边形的边数，把背景从原来的正六边形和正方形变换成正方形和正三角形，这样就得到问题4，在问题4的第(1)小题中，让学生体会特殊化思想，先满足部分条件，如在等边三角形内部先作一个等边三角形，使其中三个顶点在等边三角形的边上，然后再推广到四个顶点在等边三角形的边上，这就如同大数学家华罗庚所说“ 善于退，足够的退，退到最原始而不失重要的地方，是学好数学的一个诀窍．”在问题4的第(2)小题中，由于所求作的等边三角形的边长大小是唯一的，计算所求作的等边三角形的边长．问题5和问题6把问题4从等边三角形推广到直角三角形甚至更一般的锐角三角形．这样通过引导学生进一步改变问题条件，即将问题一般化，从而促进学生发现这一类问题的本质．通过题组形式让学生加深对题目的理解和把握，培养学生思维的深刻性．

培养学生的数学思维品质是一个重要、长期而复杂的过程．作为中学数学教师，要全面、客观地认识解题教学在培养学生思维品质方面的独特作用，从课堂的点滴做起，选择优质的数学问题，创设恰当的问题情境，挖掘数学问题的育人功能，营造主动思维的课堂氛围，促进学生积极探究问题，养成正确的思维习惯，形成良好的思维品质，以期提高数学素养和学习能力.