从“研题”、“究题”到“编题”
——以椭圆中心三角形面积研究为例
2018-07-16陈芝飞方均斌
陈芝飞 方均斌
(1.温州市第十四高级中学325000; 2.温州大学325035)
波利亚指出“解题的价值不是答案本身,而是在于弄清是怎样想到这个解法的”,数学教师离不开解题研究.研——石开也:把石头撬开,既需要耐心与勇气,更需要高屋建瓴谋全局的意识.究——九穴也:问题的表象可能扑朔迷离,需要有锲而不舍、上下求索的探究意识与探究精神.通过解题研究(简称“研题”)挖掘题目背后蕴藏的数学观点、数学思想,透过现象认识本质.研题既是高中数学教师必备素养与能力,也是教学研究的重要组成部分.那么研哪些题?怎么研题?笔者结合椭圆中心三角形面积的研究谈谈自己的收获与体会,与读者共享.
1 聚焦题源
研题的最终目的是为了学生的学,帮助学生走出题海,提高效率,减轻学生的学习负担.因此,作为高中数学教师应时常关注高考题、竞赛题、高考模拟题等,一般来说,一些频繁出现的类似问题常会引起人们的关注.笔者留意到近几年对于椭圆中心三角形(定义:设O为椭圆的中心,A、B为其上的两点,称△AOB为椭圆的中心三角形[1].)的面积考查频率较高.如

图1


图2


图3
题3(2016年温州市一模)如图3,已知椭圆C:

(Ⅱ)过点A作AP∥OM交椭圆C于点P,求证:BP∥ON.

我们自然会想到,对于给定的椭圆,其中心三角形面积决定因素是什么?定面积的椭圆中心三角形背后的数学本质又是什么?
2 研题与究题
基于这样的思考,笔者先尝试用初等的方法探索,结果发现了一个有趣的现象:椭圆的问题往往具有“圆的影子”.采取高等数学中的仿射变换,得到了一些有趣的结论,收获颇丰.
2.1 朴实无华地初等探索
聚焦题源,选定研题素材之后,接下来就是明确研题方向提出问题,解决问题.以初等方法起步,表征化归、以简驭繁.


代入化简得
(b2+a2k2)x2+2kma2x+a2m2-a2b2=0,
由Δ>0得m2 设A(x1,y1),B(x2,y2), 为了更好地识得真相,需要挖掘高等数学的背景,首先想到仿射变换. 在变换μ下椭圆C由圆O:(x′)2+(y′)2=a2纵向压缩而来(如图4), 图4 即若O到直线A′B′的距离为定值, 则椭圆中心三角形OAB面积为定值,反之亦然. 于是得到椭圆中心三角形定面积的定理: 该定理既帮助我们认识椭圆定面积的本质,也为我们提供了做椭圆定面积三角形的一个方法.以题3为例,在仿射变换的下将椭圆变换成圆,则∠APB=∠MON=90°,由仿射变换的平行不变性得证. 正如波利亚所言“好问题类似于采蘑菇,采到一个后还应四处看看,也许还有更多”,所以研题者须有上下求索的“究题”精神. 图5 证明由定理知: 联立直线与椭圆C的方程组易得线段AB中点 所以点M的轨迹方程 点M的轨迹方程是 点M的轨迹方程是 证明 得到圆O:(x′)2+(y′)2=a2, (如图6、7) 进一步得OA′⊥OB′. 图6 若λ>1,(如图6)结合圆的割线性质可得 (λ-1)(λ+1)a2 =P′G′·P′B′. 若0<λ<1,(如图7)由相交弦定理可得 图7 (1-λ)(λ+1)a2=P′G′·P′B′, (本题也可用解析法证明,有兴趣的读者可尝试) 证明直线AB斜率为k,可设直线方程为 y=kx+m, 得(b2+a2k2)x2+2kma2x+a2m2-a2b2=0, 设A(x1,y1),B(x2,y2), 又点A关于x轴的对称点为D,故D(x1,-y1); 则中心三角形△OBD面积 结合定理可以得到新的推论: 通过教师高屋建瓴地探索所得到的结论,我们的“题源”也就丰富起来了. 我们仍然以本文所得到的定理及其推论为例,就可以很自然地根据考核目的进行编写适合学生完成的各 类数学题,限于篇幅,这里不妨提供两例,解答由读者自己完成. 训练题1: C.不是定值,但有最大值D. 不是定值,但有最小值 (答案:A,结合推论3易知) 受文[4]92页(性质四十二)启发,又编得一题. 训练题2: 已知过原点的直线交椭圆x2+2y2=1于A,B两点,点P为椭圆上异于A,B的两点,弦PA,PB的中点分别记为M,N,射线OM,ON于椭圆的交点分别记为G,H,则下列三角形中面积为定值的是() A. △OMNB. △OAG C.△OPGD. △OGH (答案:D) 抓住中心三角形面积为定值的数学本质,植于“题源”,也可进一步挖掘,编出适合竞赛学生的题目. 训练题3: 高考的命题往往有高屋建瓴,立意高,入口宽,落点低的特点,作为数学教师,我们要善于思考,积极探究,了解试题背景、挖掘试题本质、从而居高临下的教学;我们要有攻坚克难的精神,持之以恒的态度,更要有解决问题的创新精神和独特智慧!我们要具备高等数学的素养和观点,做到高屋建瓴“研题”及上下求索“究题”,同时一些水到渠成的“编题”也就“不在话下”了!
2.2 高屋建瓴地“研题”



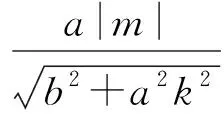


2.3 上下求索地“究题”



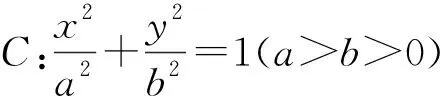
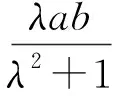










3 运用自如地“编题”