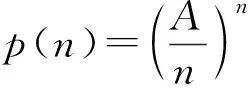核心素养怎样考(四)
2018-07-16李尚志
李尚志
(北京航空航天大学 100083)
测试题2
一、填空题:
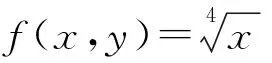
2. 若干个正整数之和等于20, 这些正整数的乘积的最大值为________.
3. 常数a,b使恒等式a(2x2+x+5)+b(x2+x+1)=x2-3x+13 成立, 则(a,b)=(____,____).
4. 设P是抛物线y2=2x上的点,Q是圆(x-5)2+y2=1 上的点, 则|PQ|的最小值是.
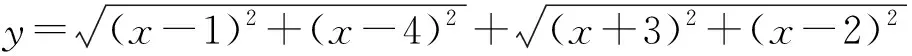
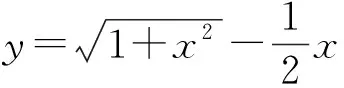
7. 在有理数范围内分解因式:x15-1=.
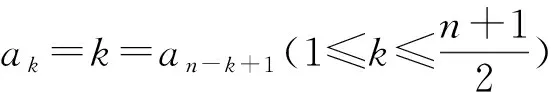
=tan________.
(提示: 考虑向量a1(cosα,sinα) +…+an(cosnα, sinnα)的方向.)
9.P是锐角∠MON=α内固定点, |OP|=r. 分别在角的两边OM,ON上选取点A,B使三角形△PAB的周长p最短, 则p=____________
.
二、解答题
x15-1=(x-1)(x-ω)(x-ω2)…(x-ω14) .
求证:x15-1 的如下因式都是整系数多项式:
f1(x)=(x-ω5)(x-ω10),
f2(x)=(x-ω3)(x-ω6)(x-ω9)(x-ω12),
f3(x)=(x-ω)(x-ω2)(x-ω4)(x-ω7)(x-ω8)(x-ω11)(x-ω13)(x-ω14).
11. 蜜蜂的蜂巢的每个蜂房的形状可以由正六棱柱按如下方式得到: 设O,O′ 分别是棱柱两个底面正六边形ABCDEF与A′B′C′D′E′F′ 的中心. 在O′O的延长线上取点Q, 过Q与A,C,E中每两个点作平面, 得到3个平面QAC,QCE,QEA, 分别交侧棱BB′,DD′,FF′于G,K,J, 得到3个全等的菱形QAGC,QAKE,QCJE. 在OO′的延长线上截取O′Q′=OQ, 过Q′与A′,C′,E′中的每两点作平面可得到与前述三个菱形全等的三个菱形Q′A′G′C′,Q′A′K′E′,Q′C′J′E′. 这六个全等的菱形与正六棱柱的各侧面围成一个蜂房, 体积与原来的正六棱柱相同. 选择点Q的位置使蜂房表面积最小, 菱形的角α=∠AQC应是多大?
12. 某产品由5 个部件装配而成, 每个部件有4种不同型号, 共需生产4×5=20种不同型号的部件, 可装配出45=1024 种不同类型的产品. 需生产的不同型号越多, 成本就越高.可装配出的产品类型越多, 用户就越欢迎. 请适当调整部件个数和每个部件的型号个数,保持不同型号的部件总数仍是20种, 使装配出的产品类型最多. 给出方案并说明理由.
13. 圆柱底面半径为r. 用一个平面斜截圆柱的侧面, 截得的侧面的最大高度为a, 最小高度为b,a>b>0.
(1) 试画出截得侧面的展开图(只须画出简图即可). 猜测截痕展开得到的曲线是什么形状的曲线.
(2) 在适当坐标系下求截痕展开所得曲线的方程. 这是什么曲线?
15. 空间中从同一点出发两两成钝角的射线最多有几条? 并证明你的结论.
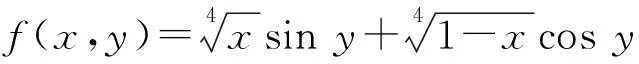
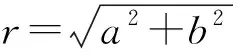
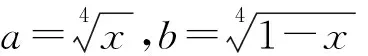
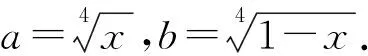
f(x,y)=asiny+bcosy
=rcosαsiny+rsinαcosy
=rsin(α+y)≤r.
=2x+2(1-x)=2,
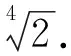
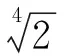
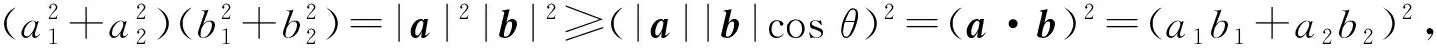
解法2由柯西不等式得
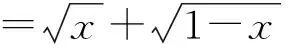
(1)
再用柯西不等式得
=2
(2)
(3)
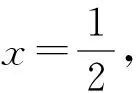
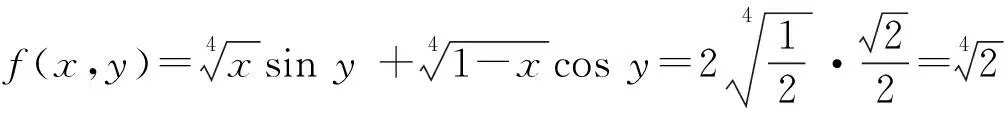
解法3设向量a,b夹角为θ, 则a·b=|a||b|cosθ.
由cosθ≤ |cosθ|≤1 得a·b≤|a·b|≤|a||b|.
等式a·b=|a||b|成立的充分必要条件是cosθ=1 或|a||b|=0.
当|a||b|≠0 时,要求cosθ=1,θ=0,a,b同向,b=λa对某个λ>0 成立. 当|a||b|=0时,a,b至少一个为0, 仍然同向.
当两个≤ 都取等号,
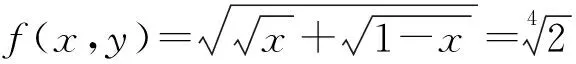
此时
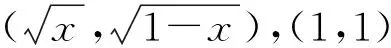
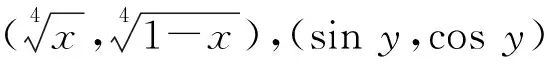
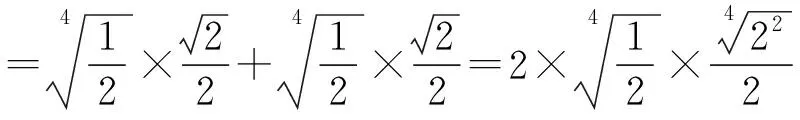
达到最大值.
借题发挥
1 一念之差, 多元函数变一元
本题可以套用求y=f(x)=asinx+bcosx最大值的现成算法:
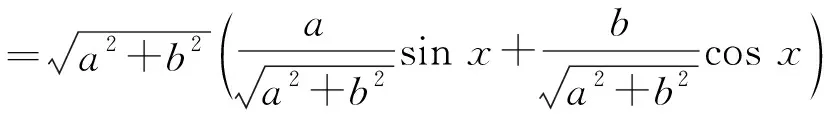
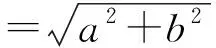
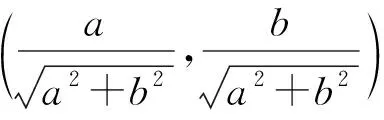
所成的角.
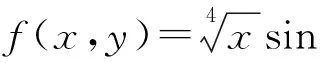
再考虑x在定义域[0,1] 内变化时M(x) 的最大值, 就是f(x,y) 的最大值.
本题考察的第一条素养不是算法, 而是看考生只会死记硬背现成算法, 还是会把x看成常数, 将asinx+bcosx的现成算法拿到这里来应用. 考的就是一念之差. 考试完了, 学的也就是一念之差. 处理多元函数的这种观念非常有用. 例如, 如下的问题曾经是研究生入学考试题, 也是中学数学竞赛题. 前者考的是大学毕业生, 后者考的是中学生.
例1x,y,z是任意实数,A,B,C是任意三角形的三个内角. 证明不等式:
x2+y2+z2
≥ 2xycosA+2xzcosB+2yzcosC.
证明不等式左右两边之差
d=x2+y2+z2-2xycosA-2xzcosB-2yzcosC
=x2-2x(ycosA+zcosB)+y2+z2-2yzcosC
=(x-ycosA-zcosB)2+y2-y2cos2A+z2-z2cos2B-2yz(-cos(A+B))-2yz·cosAcosB
=(x-ycosA-zcosB)2+y2sin2A+z2·sin2B-2yzsinAsinB
=(x-ycosA-zcosB)2+(ysinA-z·sinC)2≥0.
原不等式成立.
以上证法的要点是:
(1) 证明不等式f≥g成立, 最直接的方法证明f-g≥0. 这是不等号≥的原始定义.
(2) 证明d≥ 0 的一个重要方法: 将d配方写成实数的平方的正数倍之和.
(3) 如果d=Q(x1,… ,xn) 是多元二次多项式, 先将x2,… ,xn取值看成常数,d看成x1的一元函数d=f1(x1). 如果是d是x1的二次三项式, 可配方为
d=a1[x1-g(x2,… ,xn)]2+d2(x2,…,xn),
再将x3,… ,xn看成常数, 将d2(x2,… ,xn) 看成x2的函数f2(x2).如果f2(x2) 是x2的二次三项式, 再配方. 如果最后将d配成有限个多项式的平方的正数倍之和, 则d≥0.
在以上例题中将A,B,C看成常数, 则d是二次项之和, 称为二次型. 是大学线性代数课程的学习内容, 所以成为考研题. 但中学生也可以用配方的方法来解决. 靠的就是一念之差.
2 幂平均
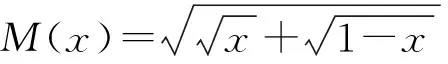
还可以再平方, 再消掉一层根号, 又产生新的根号:
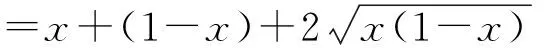
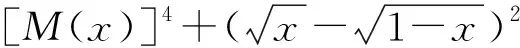
=2.
这个妙招可以推广为更一般的不等式
(u+v)2+(u-v)2=2(u2+v2) ≥ (u+v)2,
其中u,v是任意实数. 仅当u=v时等号成立.
还可改写为
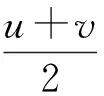
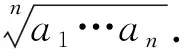
幂平均的概念可以推广到任意非零实数k. 任意有限个正实数a1,… ,an的k次幂的算术平均的k次正方根
称为a1,… ,an的k次幂平均.
Mk的大小介于所有ai的最大值与最小值之间, 当所有ai相等时,Mk也与它们相等.
特别地, 当k=1时,M1就是算术平均.
当k=-1时,
也称为调和平均.
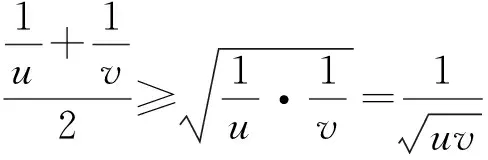
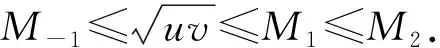
这促使我们猜想: 当u,v固定,k增加,Mk也增加.
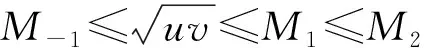
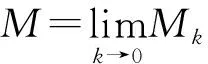
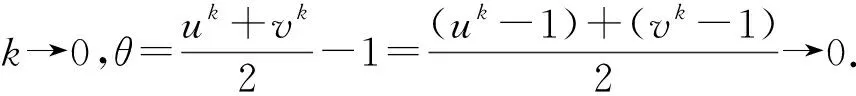


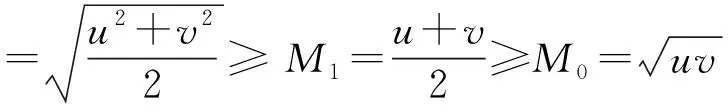
这更促使我们相信当u,v固定不变时Mk是k的递增函数.
可以证明, 对于任意n个正数a1,… ,an的k次幂平均Mk是k的递增函数, 当k>r时有Mk≥Mr, 等号仅当所有ai相等时成立.证明所用到的知识超出中学数学范围, 就不介绍了.
不过我们可以对任意n个正数证明一个特殊情形:M2≥M1.
3 柯西不等式
本题解法2从头到尾用柯西不等式, 其中a1,a2,b1,b2是任意实数.
等号成立的条件为(a1,a2),(b1,b2) 成比例, 也就是a1b2=a2b1.
sin2y+cos2y=1 消掉正余弦,
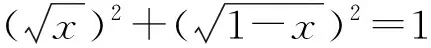
解法1没用柯西不等式, 用什么? 第一步用和角公式消正余弦. 第二步自己证明了一个不等式
仍然是靠平方和消根号. 其实是证明了
(u+v)2≤(u+v)2+(u-v)2=2(u2+v2),
同时也是柯西不等式的特殊情形:
(1u+1v)2≤(12+12)(u2+v2).
可见, 二次幂平均不等式是在柯西不等式中取b1=b2=1的特殊情形. 不过, 解法1没有引用柯西不等式, 直接证明了这个特殊情形.
解法3也不引用柯西不等式, 而是由余弦满足的不等式|cosθ|≤1得出数量积不等式|a·b|≤|a||b|来使用. 将向量a,b在平面上的标准正交基下写成坐标a=(a1,a2),b=(b1,b2), 这个数量积不等式就是
等号成立的条件是a,b共线. 这就是柯西不等式.
只不过解法2不加证明直接引用柯西不等式, 解法3先利用余弦不等式|cosθ|≤1 证明柯西不等式, 然后再使用.
空间非零向量a=(a1,a2,a3),b=(b1,b2,b3) 同样满足不等式
|a·b|=|a||b||cosθ|≤|a||b|,
即(a·b)2≤|a|2|b|2,
等号成立的条件为a,b共线. 也就是
(a1b1+a2b2+a3b3)2
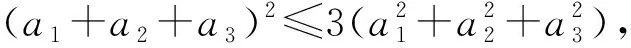
也就是:a1,a2,a3的2次幂平均不小于算术平均. 不但当a1,a2,a3为正数时成立, 为任意实数时也成立.
对任意正整数n, 可以将任意n个实数a1,…,an排成n维向量a=(a1,… ,an), 定义两个n维向量a=(a1,… ,an),b=(b1,… ,bn)的和、差、数量积, 以及a与任意实数x的乘积:
a±b=(a1±b1,… ,an±bn),
xa=(xa1,… ,xan),
a·b=a1b1+…+anbn,
还可利用数量积定义任意向量a的长度|a|, 非零向量a,b的夹角θ:
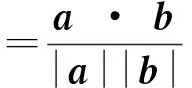
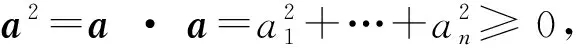
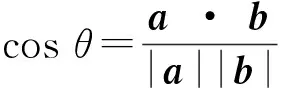
(a·b)2=(a1b1+…+anbn)2
我们证明这个不等式对任意实数a1,…,an,b1,…,bn成立. 等号成立的充分必要条件是存在λ使b=λa或a=λb.
这个不等式称为柯西不等式.
当n=2或3时a,b是几何向量, 非零向量预先就有了夹角满足|cosθ|≤1, 我们先由a·b=|a||b|cosθ定义数量积, 然后才在标准正交基下建立坐标a=(a1,a2,a3),b=(b1,b2,b3) 并推出数量积计算公式a·b=a1b1+a2b2+a3b3. 因此可以由|cosθ|≤1 得出柯西不等式|a·b|=|a||b||cosθ|≤|a||b|.
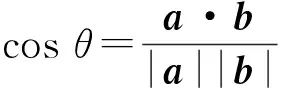
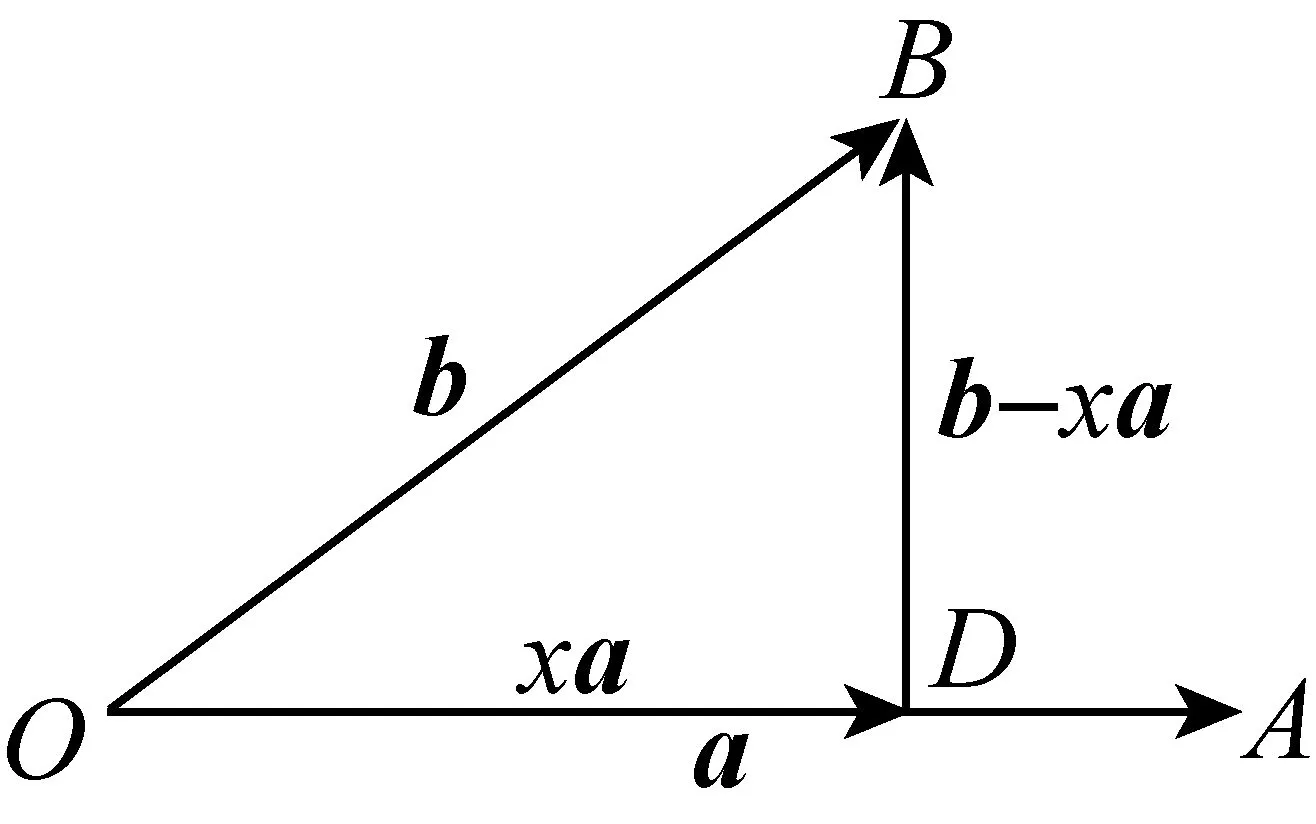
图1
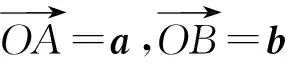
|OB|2-|OD|2=|DB|2≥0
(1)
(b-xa)2≥ 0
(2)
选x使DB⊥OA, 则勾股定理
|OB|2-|OD|2=|DB|2成立,
即
b2-(xa)2=(b-xa)2
(3)
解此方程求x. 方程两边整理得
b2-x2a2=b2-2xa·b+x2a2
(4)
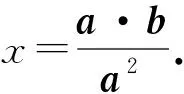
b2-x2a2=右边≥ 0,
⟹a2b2≥ (a·b)2.
这就得到了柯西不等式.
将平面向量替换成n维数组a=(a1,… ,an),b=(b1,… ,bn). 前面的几何推理(1)没有了, 向量运算的步骤(2),(3),(4) 仍然成立:
(b-xa)2=(b1-xa1)2+…+(bn-xan)2≥0
(2)
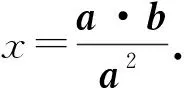
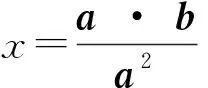
⟹a2b2≥ (a·b)2.
这就对任意n证明了柯西不等式.为什么平面向量的推理步骤(2)(3)(4)能适用于n维数组向量?因为每一步都是向量运算, 没有用到几何图形的特殊性质. 向量运算依靠的是运算律,n维数组向量同样满足这些运算律. 有两处用到运算律: 步骤(2)的不等式(b-xa)2≥ 0 对几何向量成立的原因是线段长度的平方|DB|2≥0, 数组向量成立的原因则是因为它是各分量实数的平方和. 步骤(3),(4) 解方程的关键是展开式(b-xa)2=a2-2xa·b+x2a2,用到向量点乘的交换律以及对加减法的分配律. 数组向量的点乘是对应分量乘积之和, 分配律和交换律都包含在各分量的乘法之中. 我们没有先证明这两个运算律再用来展开, 而是直接将(b-xa)2=(b1-xa1)2+…+(bn-xan)2的各项(bi-xai)2分别展开再加起来. 总而言之, 几何向量的推理之所以能够搬到数组向量, 要点是:“所以然”(运算律)没有变, “然”也就不变.
在柯西不等式中令所有bi=1 得
从而
这证明了任意n个实数的二次幂平均不小于算术平均.
题2(1) 若干个正整数之和等于20, 这些正整数乘积最大值为________
(2) 若干个正实数之和等于20, 这些正实数乘积最大值为________
解(1) 20=x1+…+xn分成正整数x1,…,xn之和. 假定乘积p=x1…xn已经最大. 如果将这n个数中某几个数替换成另外的正整数, 保持它们的和不变, 则乘积p不能增加, 只能减少或不变.
如果x1=1, 将x1与x2合并成一个数y1=1+x2, 和不变, 乘积由x1x2=x2增加到y1=1+x2>x2, 所有各数的乘积p=1x2…xn增加到(1+x2)…xn, 说明原来的p不是最大. 这说明, 当p最大, 必须x1≥2, 且所有的xi≥2.
将每个>2 的xi=2+(xi-2) 拆成2,xi-2 之和, 和不变, 乘积2(xi- 2)≤xi⟹xi≤4. 这说明所有的xi只能等于2,3,4 之一. 每个4 可以拆成两个2 之和, 乘积4 变成2×2=4 不变. 得到的2 和3 之和仍为20, 乘积最大.
如果2 的个数≥3, 将3个2换成两个3, 和2+2+2=3+3 不变.乘积2×2×2=8<3×3=9增大. 说明原来的乘积并非最大. 乘积最大的分解式中2的个数不能超过2. 只能是20=3+3+3+3+3+3+2,最大乘积为36×2=1458.
答案: 1458.
(2) 让n固定, 设n个正实数x1,… ,xn之和x1+…+xn=20.
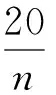
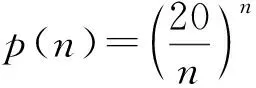

n 12345678920n20106.667543.3332.8572.52.22220n n20100296.362510241371.71554.31525.91321.6
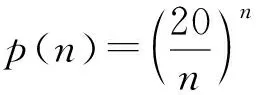
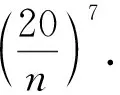
题12某产品由5 个部件装配而成, 每个部件有4种不同型号, 共需生产4×5=20种不同型号的部件, 可装配出45=1024 种不同类型的产品. 需生产的不同型号越多, 成本越高. 可装配出的产品类型越多,用户越欢迎. 请适当调整部件个数和各部件型号个数, 保持不同型号的部件总数仍是20种, 使装配出的产品类型最多. 给出方案并说明理由.
解设共有n个部件, 每个部件型号个数各为x1,… ,xn, 则部件总数x1+…+xn=20, 要使装配出的产品类型数p=x1x2…xn最多, 就是把20分成若干个正整数x1,… ,xn之和, 使它们的乘积最大.填空题2已证明: 设置7 个部件, 让其中6个部件各3种不同型号, 一个部件2种不同型号, 则不同型号的部件总数仍为3×6+2=20, 可装配出产品类型36×2=1458 最多.
借题发挥
1 抽象克无穷
以上第(2)小题由p(7)>p(8)>p(9) 断言p(n) 继续递减, 只是猜想, 缺乏证据. 虽然填空题不需要讲证据,只要求答案正确. 但你能断言答案正确吗? 也可能从p(7) 先递减到某个p(m) 再递增到某个p(N)>p(7), 你的答案就错了.
要确保答案正确, 需要继续对所有的正整数n=10,11,… 依次计算p(n), 观察它们是否递减. 所有的正整数有无穷多, 不可能全部计算. 注意到当n≥20时
一下子排除了n≥20 的无穷多个p(n), 只剩下19个n需要验证.
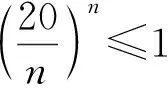
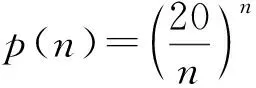
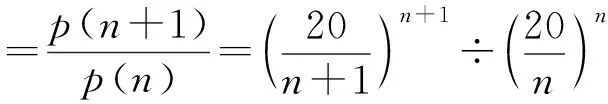
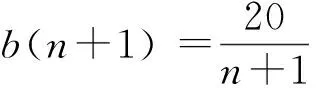
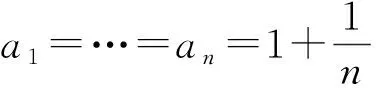
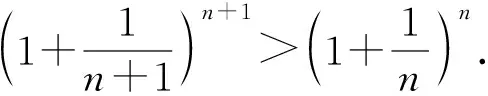
也就是e(n+1) >e(n). 这说明当n递增时, e(n) 递增.
k(n) 是递减正数b(n+1) 与递增正数e(n) 之比, 因而递减.
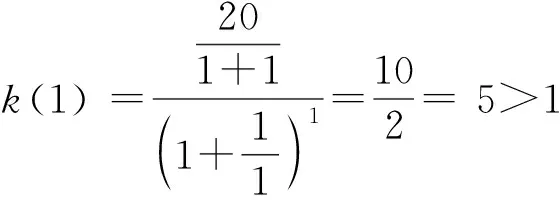
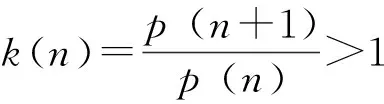
当p(n)>p(n+1) 时p(n) 递减, 0 以后的k(n) 继续递减, 始终k(n)<1.p(n)持续递减, 不再递增. 这证明了:k(n) 从k(1)>1 递减到某个k(N-1)≥1>k(N),p(n)从p(1)递增到p(N-1)≤p(N), 然后持续递减,p(N)是所有p(n)的最大值. 根据这个道理, 以上第(2)小题由 ≈1525.9, 为了找p(6) 最大值p(N) 满足的条件k(N-1) ≥1>k(N) 就是 k(n) 可以改写为 我们证明当n递增时E(n) 递减: 不等号两边取n+1次幂并且取倒数得 从p(1) 到p(m) 递增,p(m) 之前的p(1),… ,p(m-1) 都不是最大值. p(m)到p(m+1)到以后递减,p(m) 之后所有的p(j) 都不是最大值. 当n≤7时p(n) 递增, 当n≥8时p(n)递减, 当m<7或m>8时p(m) 都不是最大值. 只有p(7),p(8)有可能是最大值.具体计算得 ≈1525.9. 以上分析适用于将任意正数A分解为若干个正数之和A=x1+…+xn,求乘积p=x1…xn的最大值. 当A2 自然对数的底e
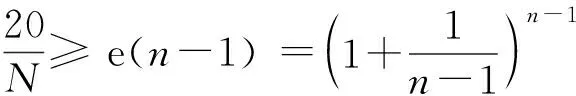
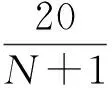
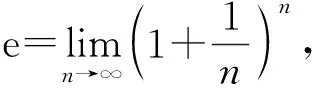
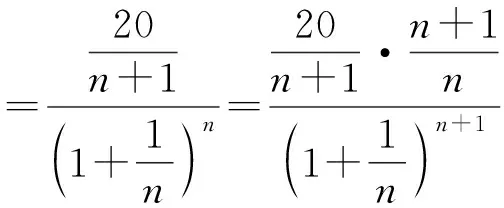
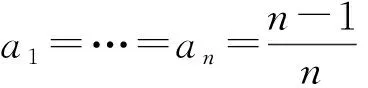
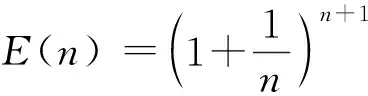
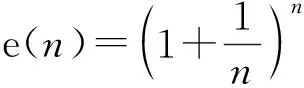
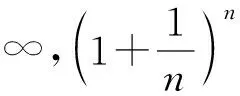
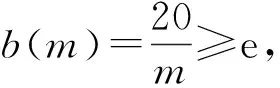
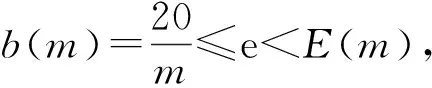
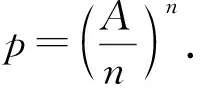
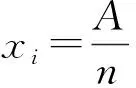
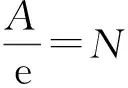
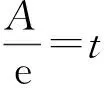
3 导数判定升降