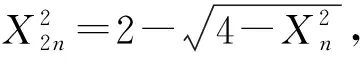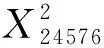小孩和我偶遇祖冲之计算圆周率之谜

邹畅根　邹源清

(南京市北京东路小学　210008)

儿子幼儿园毕业后，带他到南京东郊风景区去玩，在景区的历史文化展览馆，我们看到了祖冲之的雕像及关于他的介绍.我开玩笑让小孩拜祖冲之为师，记住圆周率π在3.1415926到3.1415927之间，并要求他在7岁之前搞清π的含义.

为了搞清楚π，我带小孩一起用细线量了树干的周长，并在阳台上画了个半径为1米的半圆如上图，用细线测量π的值(误差巨大).

原本要求小孩能理解圆周率π为圆的周长除以直径，但后来发现这个要求太低，我改变计划，要求他能用计算器算出π.

在小孩上小学一年级的时间里，教了他简单的四则运算，以及三角形特征、勾股定理等简单的几何学知识，重点是要小孩初步理解这些基础知识，以便能理解祖冲之用割圆术计算圆周率的方法.

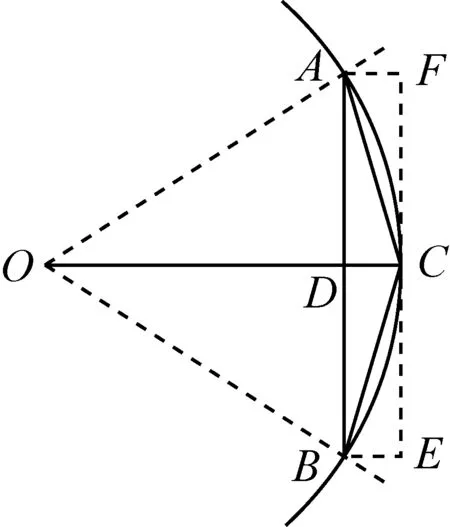
祖冲之采用更早的数学家刘徽的割圆术如右图，以圆内接正多边形的面积及其外加一个矩形面积之和，双向逼近圆的面积.

假设半径为1的圆，它的内接正n边形的边长AB为Xn、面积为Sn，内接正2n边形的边长BC为X2n、面积为S2n，假设三角形ABC的面积为S△ABC，矩形ABEF的面积为S四边形ABEF，圆的面积为S，那么

n·S△ABC=S2n-Sn，

n·S四边形ABEF=2·(S2n-Sn)

由于圆的面积大于圆内接正2n边形面积、小于圆内接正n边形面积加n个矩形ABEF的面积，所以S2n

利用三角形面积公式，可以计算出四边形AOBC的面积为AB·OC/2，所以

S2n=Xn·n/2 ，Sn=Xn/2·n/4 ，

因此圆周率π的范围如下：

Xn·n/2<π

由于筹算比较费时费力，生于数学世家的祖冲之很清楚节省运算量的重要性.上述推理仅用到了勾股定理，祖冲之利用数学家刘徽的割圆术计算圆周率，应该很容易推出上述运算量最少的计算方法，但越不过多位数的开方.

我们准备用计算器开方来算出π，但是失败了，用计算器居然无法计算出祖冲之算出的π，经仔细分析后发现，使用的计算器是12位的(例如3.12345678901，总计12位)、精度不够，因此决定在网上买个16位的计算器.

网购的计算器需要3天后才能到货，期间正好夹了个星期六和星期天，我决定带儿子一起分析祖冲之是如何做运算的.

经互联网搜索发现：祖冲之生活的年代已经用十进制计数，但阿拉伯数字还没被传入中国，算盘也没有被发明出来，计算工具是小棍子，这些小棍子称为算筹，用算筹做运算的过程称为筹算.祖冲之写了一本书叫《缀术》，其中记录了对圆周率的研究及成果，但后来这本书失传了，祖冲之如何精确计算出圆周率成为未解之谜.小孩和我用计算器都算不出祖冲之用小棍子算出的π，我们更加佩服祖冲之！中国科协主办的《科技导报》2008年第5期上，将“祖冲之究竟是怎样计算出圆周率π值的？”列为公众关注的18个未解科学难题之一.互联网上有不少分析祖冲之是如何计算π的内容，绝大部分都认为计算很困难.祖冲之计算π真像有些文章描述的那样“一双手被磨出了厚厚的老茧”吗？我决定带儿子用小棍子来试一试.

我们在摆弄小棍子的过程中，16位计算器到货了，借助于它几分钟就能将π算到祖冲之算出的3.1415926.经过几天的探索，我们发现用割圆术计算π的工作量远远没有人们想象的那么大，如果不考虑探索研究的时间，在计算不出错、动作快等前提下，筹算一两天就能将π计算到祖冲之所达到的精度.

一个小于1的小数△的平方，例如0.052比0.05小很多，将它除以一个大于1的数之后则变得更小，假设对A开方，有个大于1的数B，B2与A接近、差值为△，则可以用如下逼近方法计算：

≈B+△/2B=B+λ.

利用上面的逼近方法，每次将B的精度多提升1个小数位、步长为λ，A的逼近值每次都可以精确计算出来，其值为B2+2·λ·B+λ2，每次逼近仅需对原值做2·λ·B+λ2修正，运算量很小、而且很适合筹算.古代算筹可以有些变异，例如有人将小棍子染成不同的颜色、或采用不同的放置方法避免出错，但实质都是一样的.在本文中，算筹采用如下方法表示0 ～ 9这10个数字.

为了便于用算筹做开方运算，需要对开方过程中用的数值描述如下：

1.被开方值A；

2.A的逼近值，“A的逼近值_前”为前一次的逼近值，“A的逼近值_后”为本次逼近运算后的值；

3.开方值B，“开方值B_前”为前一次逼近的开方值，“开方值B_后”为本次逼近运算后的值，它的平方精确等于“A的逼近值_后”；

4.除数D，对2·B(用开方值B_前)做四舍五入取整(或取2·B的整数位加1)得到除数D，取值范围为4、5、6、7、8、9、10这7个数值之一(请看下面第7小点说明)；

5.差值△，为被开方值A减去“A的逼近值_前”，可能为正或负，以“开方值B_后”小数点最后一位为参考位，将被开方值及其逼近值做四舍五入取整后，再计算它们的差值；

6.步长λ，为△除以D后再做四舍五入取整，一般情况下λ小于等于5.由于D、△、λ都做了取整，因此有可能出现少量的情况下λ大于5，此时需要在不增加开方值B小数位的基础上再做一次逼近，降低被开方值与其逼近值的差值，以避免λ超过5而引入2位数的乘法运算(当然，λ大于5也没有关系，只是筹算2·λ·B略有不便)；

7.上述开方运算，对于区间 [ 3，25 )内的任何数，开方时仅会涉及到2位数除以1位数的除法以及多位数乘以1位数的乘法(乘除10因为很简单不计入2位数乘除法).对于其他情况：区间(1，3)内的数值可以先乘以4之后再开方；区间(25，100)内的数值可以先除以4之后再开方；区间(0，1)内的数值可以先乘以10的偶次方之后再开方；100以上的数值可以除以10的偶次方之后再开方.

只需要用2位数除以1位数的除法计算出步长λ及多位数乘以1位数的乘法、多位数的加减法，即可以按需要将开方的精度提升到任何所需的位数，这样的运算对筹算而言比较简单.下面举例利用割圆术计算π过程中需要开方的一个数，例如3.732050807568877，利用筹算对它进行开方运算，这是一个16位精度的数，对它开方后也要精确到小数点后15位.

·开方值整数位计算

B取2最接近；A的逼近值为4.

·开方值小数点后第1位计算

如下图，逼近值大于被开方值，步长λ为负，除数D=2·B=4，

差值△≈40-37=3，

λ=△/D≈3/4，取λ=1，

2·λ·B=2·1·2=4，

λ2=1，

A的逼近值变为 4-4·0.1+1·0.01=3.61，

B变为 2-1·0.1 = 1.9.

·开方值小数点后第2位计算

如下图，逼近值小于被开方值，步长λ为正，除数D=2·B≈4，

差值△≈73-61=12，

λ=△/D≈12/4， 取λ=3，

2·λ·B=2·3·1.9=11.4，

λ2=9，

A的逼近值变为 3.61+11.4×0.01+9×0.0001=3.7249，

B变为1.9+3×0.01=1.93.

·开方值小数点后第3位计算

如下图，逼近值小于被开方值，步长λ为正，除数D=2·B≈4，

差值△≈32-25=7，

λ= △/D≈7/4,取λ= 2,

2·λ·B= 2×2×1.93=7.72，

λ2=4，

A的逼近值变为3.7249+7.72×0.001+4×0.000001 = 3.732624，

B变为1.93+2×0.001 = 1.932.

·开方值小数点后第4位计算

如下图，逼近值大于被开方值，步长λ为负，除数D=2×B≈ 4，

差值△≈26-21=5，

λ= △/D≈5/4，取λ=1，

2·λ·B=2×1×1.932=3.864，

λ2=1，

A的逼近值变为3.732624-3.864×0.0001+1×0.00000001=3.73223761,

B变为1.932-1×0.0001=1.9319.

从上述筹算过程可以看到，开方过程仅会涉及到如下计算：2位数除以1位数的除法及多位数乘以1位数的乘法(乘除10因为很简单不计入2位数乘除法)，多位数的加减法.重复上面的运算很容易开方到第15位小数的精度，特别是筹算加减法无需要像我们常用的竖式运算那样还要重复抄写一些数字、对齐小数位也比较方便，因此熟练筹算之后，筹算速度有可能达到甚至超过我们用阿拉伯数字竖式运算.我试过筹算一次16位精度的开方大约需要1小时，祖冲之筹算的速度一定比我快很多，因此如果不考虑任何探索性时间开支，仅考虑最小运算量的情况下，祖冲之最快一天就可以将圆周率重新算一次，确定它在3.1415926与3.1415927之间.

下图用阿拉伯数字更符合现代人们的理解习惯，从图中可以很明显地看到开方的正负双向逼近过程.

3.000000000000000 (计算

3.732050807568877

3.931851652578136

3.982889722747621

3.995717846477207

3.998929174952731

3.999732275819123

3.999933067834802

3.999983266888701

3.999995816717800

经过12次开方，得到：

=0.000000261455223,

=0.000000065363807.

再经过2次开方，得到：

=0.000511326923797,

=0.000255663464343.

利用前面推导出计算圆周率π的不等式：

Xn·n/2<π

取n=24576，将X12288及X24576的值代入，可求得圆周率π的范围：

3.141592649846784<π<3.141592679884800.

通过上述14次开方，计算出圆周率π介于3.1415926和3.1415927之间.上述计算结果都是我用16位精度的计算器算出的，计算过程保留小数点后15位，如果减少1位精度，那么计算出的圆周率上限值将超过3.1415927，因此祖冲之开方的时候最少要保留16位精度.

这个开方方法有点像二分法，只是引入步长λ评估从而一次增加1个小数位，同时充分利用了前面运算的结果，每一步都确保开方值的平方精确等于被开方值的逼近值.与传统手工开方法相比，它不需要多次试乘而引入多次乘法(通过试乘规避了解二次方程，但反复试验多位数乘1位数的运算，会增加许多运算量).这个开方过程虽然有较多次数的少位数加减法，但由于仅有2位数除以1位数的除法及多位数乘以1位数的乘法(乘除10因太简单不计入2位数乘除)，因此很适合原始的筹算(当然也适合现代人用阿拉伯数字进行手工开方).现代计算机的数字运算，CPU实现多位乘除法(例如100位乘除100位)仍然具有困难，但实现多位的加减法却可以较容易地变通实现，利用上述开方方法，可用CPU快速实现多位数的高精度开方，在某些领域可能会有帮助，有兴趣的读者可以自行编写这个高精度多位开方函数.

为了说明筹算圆周率π不太困难，我拍了一个简单的视频影象放在互联网上(www.iqiyi.com和www.youku.com)，视频的名称为“儿子和我一起用小棍子精确计算圆周率”，内含我和刚上完小学一年级的儿子用算筹(小棍子)进行开方运算，我假设祖冲之开方时精确到小数点后17位，让小孩筹算一个18位有效数字(1个整数位，17个小数位)的开方值，精确到小数点后17位.