边坡稳定极限分析斜条分上限法的全局优化方法

孙　平，陈　玺，王玉杰

（1.中国水利水电科学研究院 岩土工程研究所，北京　100048；2.西安理工大学 水利水电学院，陕西 西安　710048）

1　研究背景

极限平衡法与极限分析上限法是工程中解决边坡稳定问题的两种常用方法。极限平衡法只考虑力与力矩平衡条件，不考虑变形协调条件，本质上是一种近似方法，需要引入假定才能使问题变为静定。此外，极限平衡法获得的解不受塑性力学上限或下限定理的支持，既不是一个上限解，也不是一个下限解［1］。极限分析上限法基于塑性力学的上限定理，通过在滑坡体内部构筑一个机动许可的速度场，利用功能平衡方程求解边坡安全系数，理论基础严格。Donald等［2］提出了对土条进行斜条分的极限分析上限方法，该方法将滑坡体离散为一系列具有倾斜界面的条块，在假定滑坡体的底滑面与条块界面同时达到极限状态的条件下，应用Mohr-Coulomb相关联流动法则建立一个机动许可的速度场，再利用虚功原理求解安全系数。陈祖煜等［3］在此基础上开发了岩质边坡稳定分析上限法程序EMU，极大地推动了这一方法在水利水电工程中的应用［2-4］。

临界滑动模式的搜索是边坡稳定分析中十分关键的一步。在二维极限平衡法领域，众多学者在应用最优化方法搜索临界滑裂面方面开展了深入的研究工作，取得了丰富的成果［5-12］。应该说，无论是圆弧滑裂面还是任意形状滑裂面，搜索安全系数的整体极小值问题已经得到较好的解决［5］。在二维极限分析斜条分上限法领域，由于待优化变量中包括了滑裂面位置与条块界面倾角，导致自由度与非线性程度大大增加，寻找安全系数的整体极小值变得十分困难。Donald［2］以滑面控制点坐标与条块界面倾角作为待优化变量，应用单纯形法与随机搜索法相结合搜索临界滑动模式。吴超等［13］将改进遗传算法应用于地基承载力临界滑动模式的求解，但该方法不仅需要人为指定自变量搜索范围，而且搜索过程中还需要剔除大量不合理的滑动模式，计算效率较低。Leshchinsky［14］提出将离散组合优化方法（Discontinuity layout optimization，即DLO）与极限分析上限法相结合（DLO-LA），寻找复杂边坡最小安全系数对应的临界滑动模式。该方法的基本思想是，在边坡内部与表面预先布置一系列均匀分布的网格点，试算滑裂面与条块界面均由网格点的连线组成，并采用动态规划法进行临界滑动模式的搜索。该处理方式试图将连续的优化问题转化为离散优化问题，使计算精度与结果严重依赖于网格点的布置。当前，应用最优化方法搜索斜条分上限法滑动模式的研究成果相对较少，且无法保证在任何情况下都收敛到全局最优解［3］。

边坡稳定极限分析斜条分上限法中临界滑动模式的搜索，本质上是一个工程的极小值问题，通过构造合理的优化模型，将这一工程上的极小值问题转化为数学上的极值问题，是十分关键的一步。本文通过对滑裂面控制点坐标与条块界面倾角引入一系列的约束条件，避免在随机搜索过程中生成不合理滑动模式，进而提出滑裂面通过与不通过软弱夹层两种情况下斜条分上限法滑动模式的优化模型，将该模型与全局优化方法结合，寻找边坡的临界滑动模式，并通过一系列经典算例的对比分析，对本文提出的方法的可行性与有效性进行验证。

2　边坡稳定极限分析斜条分上限法

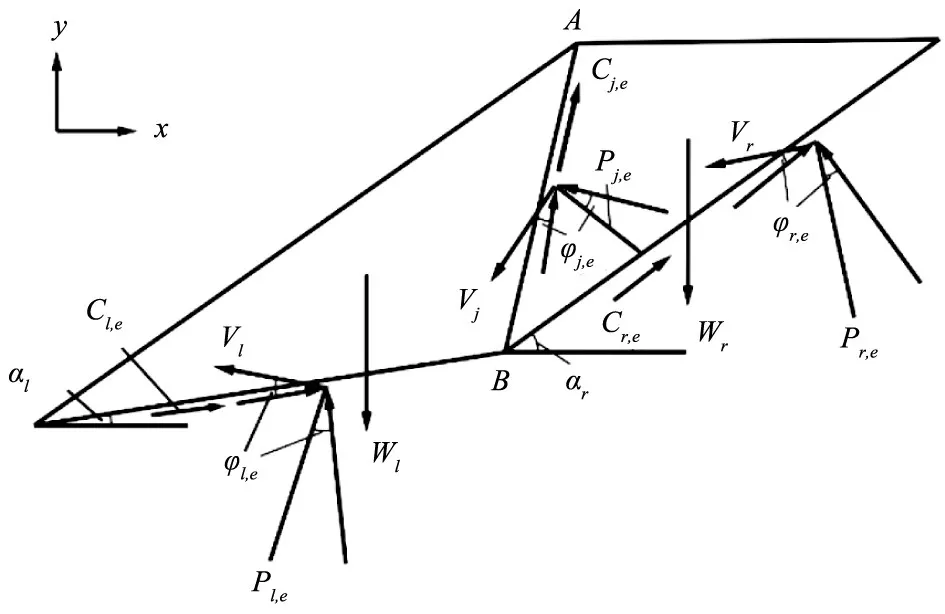
图1　双块体滑动模式的速度场

极限分析斜条分上限法假定，当滑坡体处于极限状态时，底滑面与分界面同时达到极限状态。本文以图1所示的两个块体组合的平面滑动问题为例进行说明。

首先引入破坏面上“组合摩擦力”概念。破坏面上的抗剪力可分为两部分：一部分为“凝聚力”，其值为ceA，A为破坏面面积；另一部分为法向力N与由N确定的摩擦阻力N tanφe的合力，称之为“组合摩擦力”。变量中下标‘e’表示破坏面上的抗剪强度指标tanφ与c经安全系数F折减后的值，即：tanφe=tanφ/F，ce=c/F。

对左、右块体分别建立静力平衡方程，有：

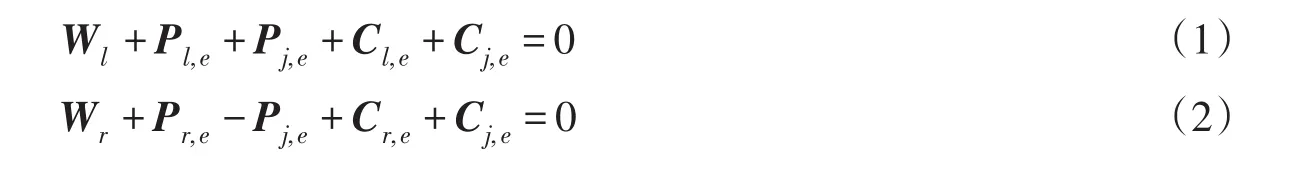
式中：Wl、Wr分别为左、右块体的体积力；Pl,e、Pr,e、Pj,e分别为左、右块体底滑面及条块界面AB上的组合摩擦力；Cl,e、Cr,e、Cj,e分别为左、右块体底滑面及条块界面AB上的凝聚力。

极限分析定理假定材料服从相关联流动法则［1］。基于这一假定，已经证明Mohr-Coulomb材料发生剪切破坏时，破坏面上的塑性速度V与破坏面的夹角为内摩擦角φ［1，3］。左、右块体的塑性速度分别用Vl和Vr表示，与底滑面夹角分别用φl,e和φr,e表示，在条块界面AB上，左块体相对右块体的塑性速度Vj为：

同理，Vj和AB的夹角为条块界面的摩擦角φj，e。

可以证明，破坏面上的组合摩擦力与塑性速度垂直。本文结合图2进行说明。

如图2所示，设线段AB为边坡内任意一个破坏面（即底滑面或条块界面）。当滑坡体达到极限状态时，作用于该面上的法向力N与抗剪力T满足Mohr-Cou⁃lomb屈服准则，即：

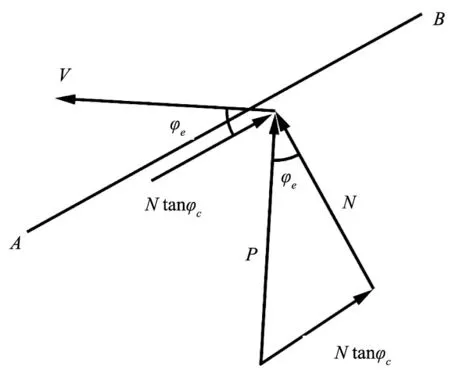
图2　破坏面上的组合摩擦力P与塑性速度V

式中：φe、ce分别为AB面上经安全系数F折减后的摩擦角与凝聚力；A为AB面的面积。

如前所述，AB面上的组合摩擦力P为法向力N与摩擦阻力N tanφe的合力，则P与破坏面法向方向的夹角为φe。同时，因塑性速度V与AB面之间夹角为内摩擦角φe，故P与V垂直。

令左、右块体所受的力分别沿塑性速度Vl和Vr做功，由于作用在底滑面和条块界面上的组合摩擦力、和分别与 Vl、Vr和 Vj垂直，故这些内力沿该位移作的功均为零。

根据虚功原理，令：式（1）×Vl+式（2）×Vr，有

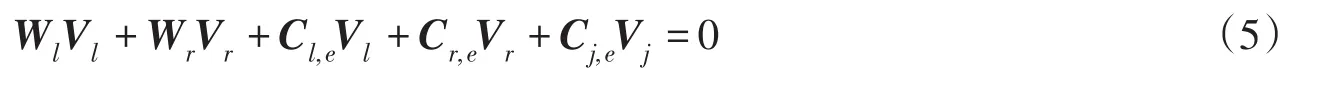
式（5）的标量表达式为：

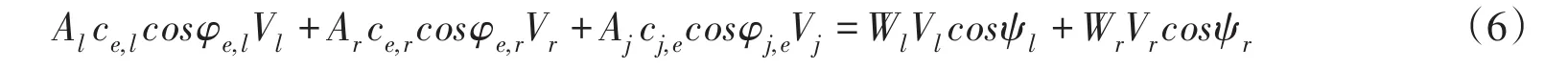
式中，ψl、ψr分别为左、右块体的体积力与Vl和Vr的夹角。

式（6）中包含4个未知量，即Vl、Vr、Vj以及隐含于下标‘e’中的安全系数F。由于Vr、Vj均可表达成Vl的线性函数［3］，故等式两侧的Vl、Vr、Vj均可消去，这样式（6）中仅包含唯一的未知量F，可采用迭代法进行求解。

上述双块体滑动模式的求解方法可以很方便的推广到多块体滑动模式。

3　斜条分上限法滑动模式的优化模型

图3　边坡几何模型

3.1边坡几何模型定义与约束条件在如图3所示的坐标系中，一般将边坡剖面简化为由若干线段组成的图形，定义其几何模型如下：y=o（x）为坡面线；y=w（x）为软弱夹层线；y=b（x）为底边界线；y=s（x）为滑裂面曲线。

在二维边坡稳定分析中，通常用m个控制点A1，A2，…，Am以直线或光滑曲线连接来模拟任意形状滑裂面，其坐标分别用（x1，y1），（x2，y2），…，（xm，ym）表示，令x1＜x2＜…＜xm。各控制点的条块界面与坡面线的交点用Bi（i=2，3，…，m-1）表示，规定条块界面倾角θ为AiBi与y轴正向的夹角，由正y方向转向正x方向为正。

此外，软弱夹层线y=w（x）被简化为由n个点M1，M2，…，Mn组成的多段线，其坐标分别用（wx1，wy1），（wx2，wy2），…，（wxn，wyn）表示，令wx1＜wx2＜…＜wxn。当软弱夹层的厚度与边坡高度相比可以忽略不计时，按无厚度处理［3］。规定在优化的过程中，滑裂面控制点A2与Am-1分别在线段M1M2与Mn-1Mn上移动。

边坡抗滑稳定安全系数F可表示为:

滑裂面的相邻控制点之间采用等分方式进一步细分条块，并约定各细分点的条块界面为各细分点与相邻两控制点条块界面交点的连线，如图3所示。

优化过程中为避免构造不合理滑动模式，引入以下约束条件：

（1）滑裂面为下凸形。

（2）除剪入与剪出段外，滑裂面不能与坡面线相交。

（3）相邻控制点所在的直线与x轴的夹角αi应控制在一个合理的范围内［5］，即：-45°≤ αi≤ 80°。

（4）相邻控制点的条块界面不能在坡体内相交。

（5）条块界面倾角θi应在一个合理的范围内［14］，即：-90°＜θi＜90°。

3.2滑裂面不通过软弱夹层时滑动模式的构造步骤

3.2.1确定滑裂面剪入点与剪出点x坐标的变化范围如图4所示，根据边坡的几何形状，滑裂面的剪入点A1与剪出点Am在水平方向的变化范围分别用［Lmin，Lmax］与［Rmin，Rmax］表示。用无量纲的标准变量表示，有：

当点A1与Am的x坐标确定后，其y坐标可由函数y=o（x）唯一确定。

3.2.2确定滑裂面中间控制点A2，A3，…，Am-1的x坐标的变化范围为使任意滑裂面构造更为灵活，将（x1，xm）进行m-2等分（图5），各分点ai的计算式为：

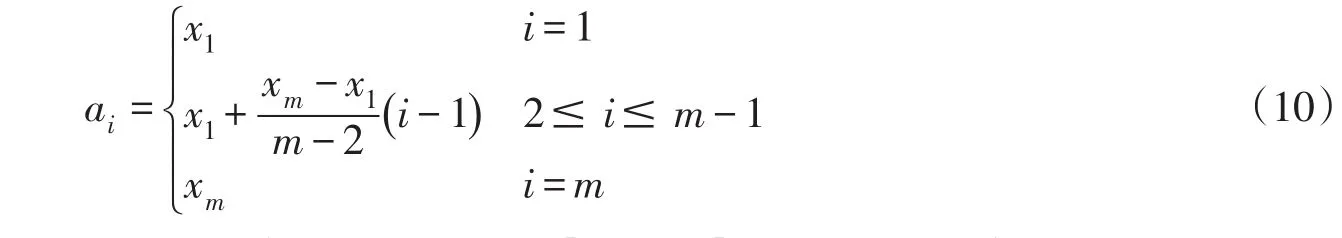
滑裂面中间控制点Ai（i=2，…，m-1）x坐标的变化范围为［ai，ai+1］，用无量纲的标准变量表示，有

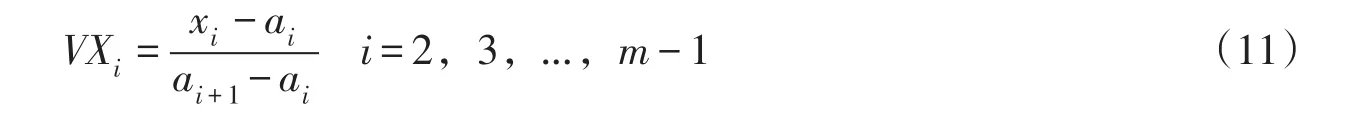
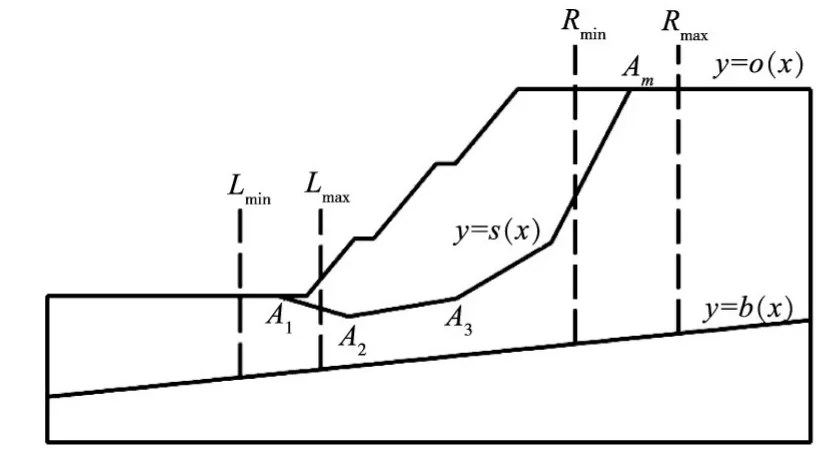
图4　滑裂面剪入与剪出点坐标的确定　

图5　滑裂面中间控制点x坐标变化范围

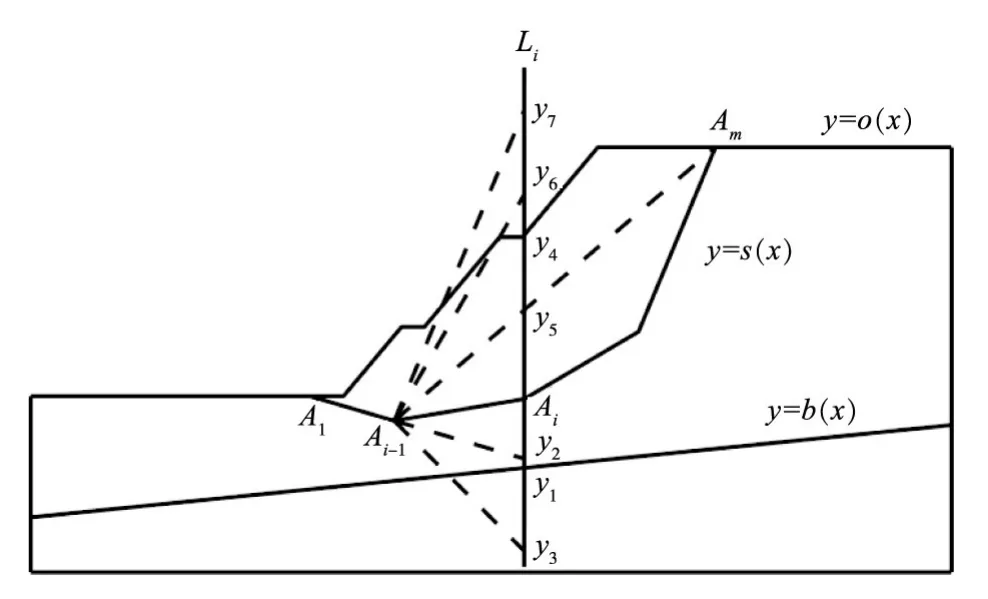
图6　滑裂面中间控制点y坐标变化范围

3.2.3确定滑裂面中间控制点Ai的y坐标的变化范围［yi，min，yi，max］如图6所示，过滑裂面控制点Ai（i=2，…，m-1）的竖直线用Li表示。

下限yi，min的确定方法为：

（1）控制点位于底边界y=b（x）的上方。直线Li与曲线y=b（x）求交，交点的y坐标用y1表示；

（2）根据约束条件1，直线Ai-2Ai-1与Li求交，交点的y坐标用y2表示；

（3）根据约束条件3，过点Ai-1且与水平线夹角为-45°的直线与直线Li求交，交点的y坐标用y3表示。则 yi，min=max（y1，y2，y3）。

上限 yi，max的确定方法为：

（1）直线Li与曲线y=o（x）求交，交点的y坐标用y4表示；

（2）根据约束条件1，直线Ai-1Am与直线Li求交，交点的y坐标用y5表示；

（3）根据约束条件2，令P表示x坐标在［xi-1，xi］之间的坡面线端点的集合，即：

过点Ai-1与集合P中所有点的直线与Li求交，交点y坐标的最小值用y6表示；

（4）根据约束条件3，过点Ai-1且与水平线夹角为80°的直线与直线Li求交，交点的y坐标用y7表示。则yi,max=min（y4，y5，y6，y7）。用无量纲的标准变量表示，有：

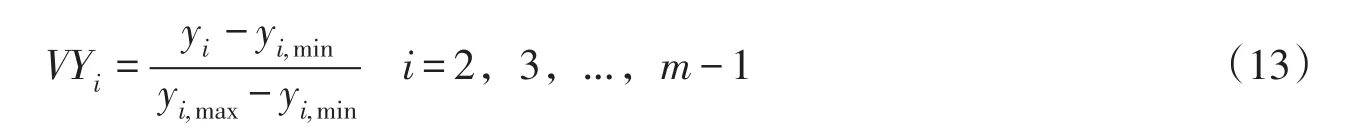
3.2.4确定条块界面倾角θi的变化范围［θi,min，θi,max］条块界面倾角的变化范围如图7所示。

下限θi,min的确定方法为：

（1）线段AiAi-1与y轴正向的夹角，记为β1；

（2）根据约束条件5，令β2=-90°；

（3）根据约束条件4，记线段AiBi-1与y轴正向的夹角，记为β3。则θi,min=max（β1，β2，β3）。

上限θi,max的确定方法为：

（1）根据约束条件4，令β4=θi-1；

（2）根据约束条件5，令β5=90°；

（3）线段AiAm与y轴正向的夹角，记为β6。则θi，max=min（β4，β5，β6）。用无量纲的标准变量表示，有:

3.3滑裂面通过软弱夹层时滑动模式的构造步骤

3.3.1确定位于软弱夹层上的滑裂面如图8所示，滑裂面控制点A2在线段M1M2上移动，其x坐标的变化范围为［wx1，wx2］，用无量纲的标准变量表示，有:

图7　条块界面倾角的变化范围

图8　滑裂面剪入与剪出段倾角的变化范围

同理，点Am-1在线段Mn-1Mn上移动，其x坐标的变化范围为［wxn-1，wxn］，用无量纲的标准变量表示，有:

3.3.2确定滑裂面剪出段A2A1与x轴负方向的夹角α的变化范围［αmin，αmax］滑裂面剪入与剪出段倾角的变化范围，如图8所示。

下限αmin的确定方法为：

（1）滑裂面剪出点A1在坡面线上。记坡面线的左端点为E，线段A2E与x轴负方向的夹角记为α1；

（2）根据约束条件1，线段A3A2与x轴负方向的夹角记为α2。则αmin=max（α1，α2）。

上限αmax的确定方法为：

由约束条件3确定上限αmax=80°。用无量纲的标准变量表示，有：

3.3.3确定滑裂面剪入段Am-1Am与x轴正方向的夹角β的变化范围［βmin，βmax］

下限βmin的确定方法为：

（1）滑裂面控制点Am在坡面线上。记坡面线的右端点为F，线段Am-1F与x轴正方向的夹角记为β1；

（2）根据约束条件1，线段Am-2Am-1与x轴正向的夹角记为β2。则βmin=max（β1，β2）。

上限βmax的确定方法为：

由约束条件3确定上限βmax=80°。用无量纲的标准变量表示，有：

条块界面倾角θi的变化范围的确定方法与前文相同，故不再赘述。

3.4最优化数学模型与优化求解综上所述，对于滑裂面不通过软弱夹层的情况，建立的优化模型为：

对于滑裂面通过软弱夹层的情况，其最优化数学模型为：

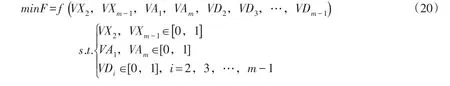
可以看出，通过建立斜条分上限法滑动模式的数学模型，滑动模式的搜索问题转化为一个多自由度的有界约束极小值问题。下文将遗传算法（GA）和粒子群算法（PSO）这两种在工程中应用广泛的全局优化算法与本文方法相结合，开展临界滑动模式的搜索计算。

4　算例分析

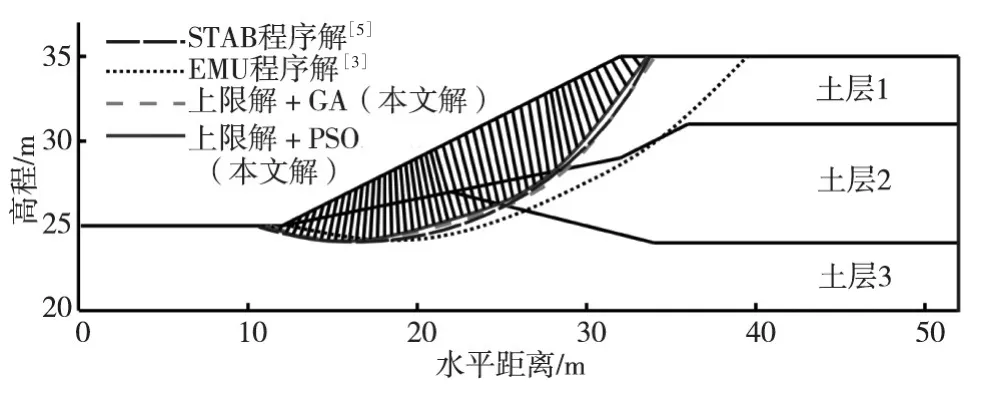
图9　边坡剖面及不同方法获得的临界滑动模式

4.1算例1：ACADS考核题1（c） 本算例为一个无软弱夹层的非均质土坡，如图9所示，各土层的物理力学参数如表1所示。文献［5］与文献［3］分别采用STAB程序（Bishop简化法+单纯形法）与EMU程序（斜条分上限法+单纯形法）对该边坡进行了稳定性计算。建立斜条分上限法的优化模型时，滑裂面控制点数为5，总自由度个数为11，各控制点之间采用光滑曲线连接。图9列出了不同方法获得的临界滑裂面位置，表2列出了不同方法的计算结果。

由计算结果可知，本文方法获得的临界滑动模式与STAB程序解十分接近，安全系数也明显小于EMU程序解。此外，本文方法得到的安全系数略大于STAB程序解，表明本文方法获得的是一个合理的、略大于极限平衡解的上限解。

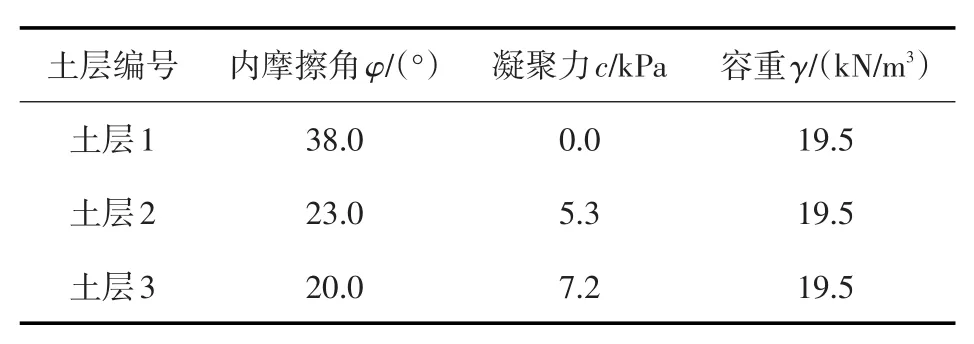
表1　ACADS考核题1（c）的物理力学参数

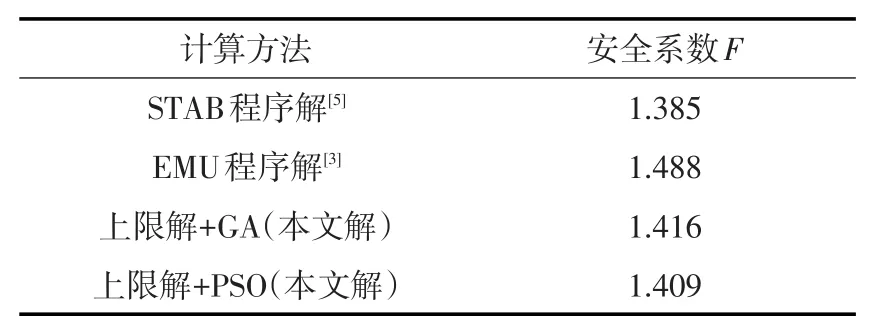
表2　不同计算方法的计算结果

4.2算例2：ACADS考核题EX3如图10所示的非均质边坡，在边坡底部发育有一层产状水平、力学性质较差的软弱夹层，即土层2。各土层的物理力学性质见表3。文献［5］采用STAB程序（Spencer法+单纯形法）对该边坡进行了稳定性分析。由于本算例为典型的沿软弱夹层滑动的问题，本文将土层2按两种方式处理：（1）土层2作为一种“普通”土层，滑裂面控制点数为4，自由度为8，滑裂面控制点之间采用直接连接；（2）土层2作为无厚度的软弱夹层，假定滑裂面经过其底边界，滑裂面控制点为4，自由度为6。为进行对比研究，采用EMU程序（上限解+单纯形法）对该算例进行了计算。图10～图11显示了不同方法获得的临界滑裂面，表4列出了不同方法计算得到的安全系数。

由计算结果可知，针对土层2的两种处理方式，基于本文提出的优化模型，采用两种优化方法得到的临界滑动模式十分接近，安全系数略大于STAB程序解，且小于EMU程序解。此外，土层2按第（1）种处理方式得到的安全系数略小于第（2）种处理方式的计算结果，表明土层2的厚度对边坡稳定安全系数有一定的影响，但影响不大。总的看来，采用本文方法获得的是一个相对较优的、合理的上限解。

表3　ACADS考核题EX3的物理力学参数

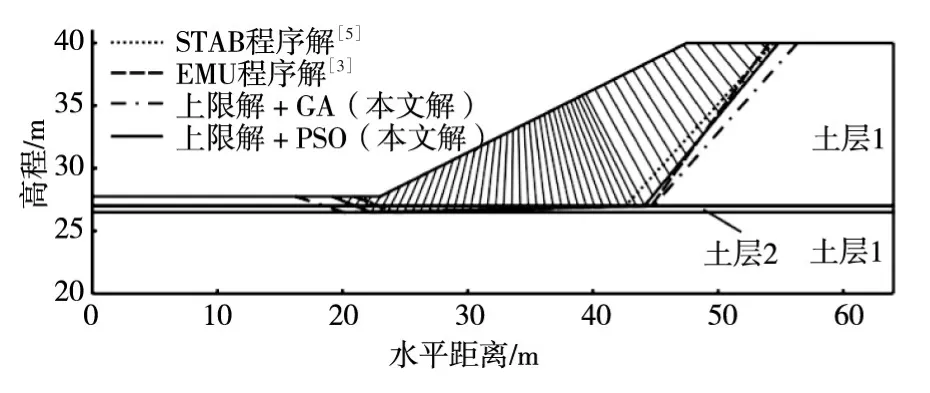
图10　土层2作为普通土层时的临界滑动模式

图11　土层2作为软弱夹层时的临界滑动模式

表4　不同方法获得的最小安全系数计算结果

4.3算例3：无重力地基极限承载力算例图12所示为无重量承载垂直表面荷载的地基极限承载力问题。1960年代，Skolovvskii［15］采用滑移线理论提出了这一问题的解析解。地基承载力是土力学的经典稳定问题之一，常作为极限分析方法的标准考题而被广泛引用［3］。在地基承载力领域，通常用加载系数代替传统的安全系数来表征其安全储备能力。若边坡表面作用有荷载q0，通过不断增加这个荷载，直至边坡达到极限状态的荷载q，则定义加载系数η为：

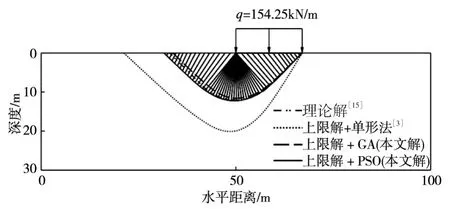
图12　无重量地基承载力问题

表5　不同方法获得的计算结果对比

本算例计算参数：基础宽度B=17m，地基土体内摩擦角φ=0°，c=30 kPa，容重γ=0 kN/m3，Prandtl解获得的地基土极限承载力qu=154.25 kPa。

令q0=qu=154.25 kPa，以加载系数η作为目标函数，滑裂面控制点个数为5，用光滑曲线连接，最右侧滑裂面控制点坐标在优化过程中保持不动，自由度个数为10。文献［3］采用上限解+单纯形法对本算例进行了计算。不同方法得到的计算结果如图12与表5所示。

从计算结果可以看出，采用本文方法得到的临界滑动模式中，条块界面均收敛到一点，加载系数η小于0.04，与理论解非常接近，且明显优于采用上限解+单纯形法的解。

5　结论

本文提出了一种边坡稳定斜条分上限法滑动模式的优化模型，该模型针对滑裂面通过与不通过软弱夹层两种情况，对滑裂面的控制点坐标与条块界面倾角引入一系列的约束条件，使滑动模式的优化问题转化为一个具有多自由度的有界约束的极小值问题。

多个典型算例的验证与对比分析表明，本文提出的数学模型与遗传算法、粒子群算法等全局优化方法相结合，具有较好的全局收敛性。特别地，对于破坏机构复杂的地基承载力问题，本文方法能够给出一个合理的、与理论解十分接近的上限解。