基于传递熵的水电站厂房振动传递路径识别

王海军，王　宁，练继建

（1.天津大学　水利工程仿真与安全国家重点实验室，天津　300350；2.天津大学 建筑工程学院，天津　300350）

1　研究背景

随着水电站装机容量和引用水头的增加，其尺寸更加庞大，刚度也逐渐降低，机组振动、流道水流等诱发的厂房结构振动问题日益引起重视［1］。水电站机组与厂房振动系统是一个庞大的耦合体系，引起其振动的主要振源包括水力、机械和电磁因素三个方面。水电站厂房振动主振源的振动传递路径识别和传递规律成为研究的难点［2］。针对水电站厂房结构振动传递路径问题，王海军等［3］基于结构声强和有限元理论对水电站厂房不同部位进行了结构声强计算，实现了传递路径的矢量可视化。余桐奎等［4］基于多种相干函数的信息相似性方法实现了双体船振动噪声源主要传递路径的识别。徐伟等［5］通过功率流理论对水电站厂房结构低频尾水脉动压力振动传递路径进行了理论分析和数值计算。毛汉领等［6］利用常相干和偏相干分析模型研究了水电站厂房发电机层楼板振动的振源以及激振力在厂房结构之间的传递路径。

基于工作环境激励下的水电站厂房结构振动原型观测可以在保证水电站正常运行的工作条件下，获得所需的振动参数及响应。但是，由于观测环境的复杂性，通过原型观测获得的振动信号不可避免会受到噪声的干扰，影响后续的数据分析。因此，滤波降噪也是结构振动分析与控制中一项重要环节。

本文基于传递熵理论对振源传递路径进行识别，通过对模拟信号的分析验证了该理论的合理性和有效性。以一大型水电站地下厂房为研究对象，首先使用基于EMD的小波熵自适应阈值去噪方法对原型观测数据去噪，然后对去噪后的信号进行小波分解与重构获取尾水涡带信号，最后利用传递熵理论对尾水涡带的垂向传递路径进行了分析，并计算了机组与结构不同测点之间的信息传递率。

2　振动传递路径识别理论及方法

2.1传递熵理论传递熵（transfer entropy）是Schreiber于2000年在香农熵、时滞交互信息基础上引申提出的［7］。传递熵本质上由多个信息熵构造而成，它不需要假定变量间具有特定形式的关系，是不同信号之间自相关和互相关函数的非线性函数，是一个动态过程关于另一个动态过程所产生的传递信息，可以度量动态过程中随机变量之间信息传递的强度，估计不同信息流之间相关程度，量化信息流之间的传递关系，揭示信息传递方向特征。现已广泛运用于生理学、金融经济学、机械结构损伤识别等学科领域［8-9］。

对于两个平稳的马尔可夫过程x和y，如果y影响x的转移概率为p，按照Schreiber定义的传递熵，这两个过程之间的耦合关系可以用下式表达［10］：

Nichols和Overbey等建议在描述结构的动态信息之间的传递关系时，可以假设过程x和过程y均为一阶马尔科夫过程，即k=l=1。通过这种假设可以避免计算传递熵时评估复杂的高维概率密度函数，但是这种假设并不影响我们利用传递熵判断进程之间的方向性和相关程度［7，11-14］。对于两个均为一阶（k=l=1）马尔可夫过程的、各态历经的、高斯的时间序列，计算传递熵时不再需要评估上式中多种不同的条件概率，通过计算不同延滞时间的自相关和互相关系数，上式可以化简为［8，15-16］：

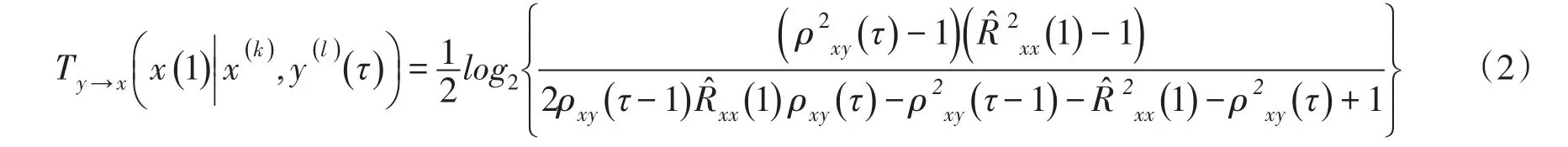
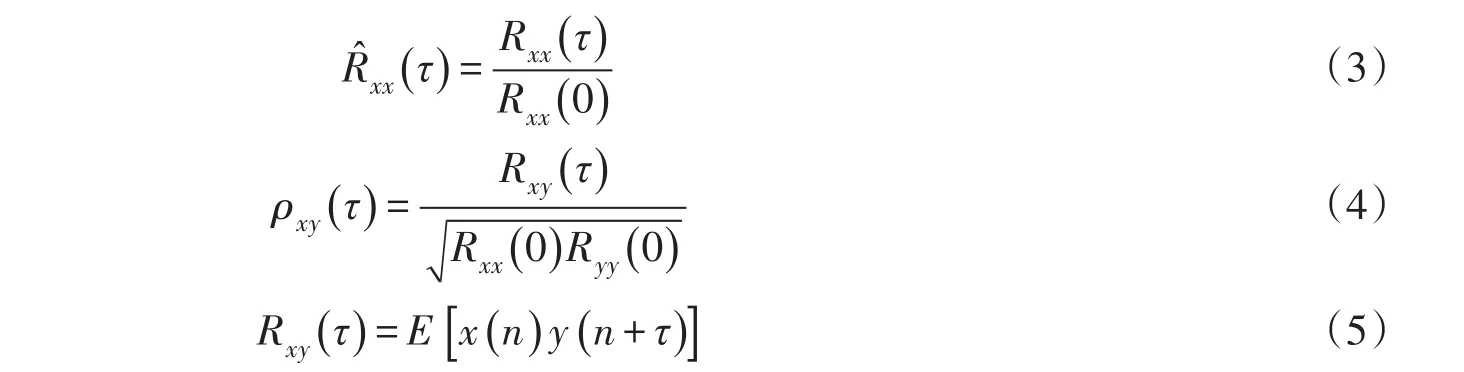
2.2EMD基本原理经验模态分解（EMD），是由N.E.Huang于1998年提出的一种数据驱动的自适应信号时频处理方法，特别适用于非线性、非平稳信号的分析处理，EMD分解的目的是对信号进行平稳化处理。它基于数据自身的时间尺度特征来进行信号分解，不需要预先设定任何基函数。信号经过EMD分解后，其振荡结构特征和非平稳性可以通过一系列内在的本征模态函数（IMF）分量和一个剩余趋势项来揭示，其中IMF分量需要满足以下两个条件［17］：

（1）其极值点和过零点的数目相等或者最多相差一个；

（2）连接其局部极大值和局部极小值形成的两条包络线的均值在任一点处为零或近似为零。

经过EMD分解后的信号可表示为：

式中：ci(t)为不同阶的IMF分量；rn(t)为趋势项。

通常分解后的各个IMF分量按频率段由高到低排列，IMF分量所包含的频率成分随信号本身变化，可以较好地反映特定时间尺度上信号的局部频率特性，因此EMD方法是一种自适应的信号分析方法。

2.3小波熵自适应阈值选取方法对含噪声信号进行小波变换后，有用信号集中于低频小波系数，噪声信号集中于高频小波系数，可以根据该特征对信号进行小波阈值去噪，而阈值的选择在小波阈值去噪中起关键作用，直接决定去噪的效果。小波熵可以衡量不同尺度的矩阵化的小波分解系数的稀疏程度，不同分解尺度上的小波熵值大小不同，因此可以根据信号小波熵特征自适应地确定对应尺度的去噪阈值，进而去除含噪信号中的噪声［18-19］。

小波熵自适应阈值的选取步骤如下：

（1）对振动信号进行j层小波分解，将每个尺度的高频小波系数分为n个独立相等的子区间，N为彩样点数，j尺度第k个子区间高频小波系数dj（k）对应的能量为：

（2）j尺度第k个子区间包含的能量在该尺度上细节部分总能量中的概率为：

（3）第k个子区间的小波熵为：

（4）噪声最集中的子区间的小波熵值最大，此区间的小波系数是由噪声引起的，将此区间的方差作为噪声估计方差，利用Donoho［20］提出的公式计算去噪阈值。

噪声估计方差：

去噪阈值为：

小波熵阈值去噪既能发挥小波局域化分析的特点，又能根据高频小波系数的疏密程度有效地抑制信号中的无关分量，在一定程度上减少阈值选取的盲目性，可以较为准确地提取信号中的主要信息量。

2.4基于EMD的小波熵自适应阈值去噪算法对于含噪信号，如果直接舍弃高阶IMF分量，会丢失高阶分量中的有用成分，因此为了最大程度地保留有用信号，有必要对信号高阶IMF分量进行去噪。本文提出的基于EMD的小波熵自适应阈值去噪算法的流程如下：

（1）首先对原始振动信号进行EMD分解；

（2）将具有噪声特性的高阶IMF分量进行小波分解，得到各尺度下的近似系数和细节系数；

（3）将各尺度下的细节系数作为独立的信号处理，按照上述的小波熵自适应阈值选取步骤计算相应的小波熵自适应阈值，然后进行小波阈值去噪，可以得到去噪后的细节系数；

（4）将去噪后的细节系数与近似系数进行小波重构得到去噪后的IMF分量；

（5）再次利用去噪后IMF分量与未经处理的IMF分量重构，可得到去噪后的重构信号。

该方法结合了EMD和小波熵阈值去噪理论，可以自适应地根据信号能量特征确定相应的去噪阈值，在一定程度上弥补了小波阈值去噪的缺陷。

3　仿真信号验证

为了将传递熵理论应用到水电站厂房结构振源传递路径分析中，首先需要检验传递熵计算模型的合理性和有效性，并分析噪声对传递熵大小和特征的影响。首先构造出两个相互关联的信号，利用传递熵模型计算不同方向、不同时间延迟下的传递熵；然后在模拟信号中加入噪声信号，计算加噪信号间的传递熵，分析噪声对传递熵的影响。

首先构造时域信号A、B，其中f1=40 Hz，f2=3 Hz，获得两个时域信号：

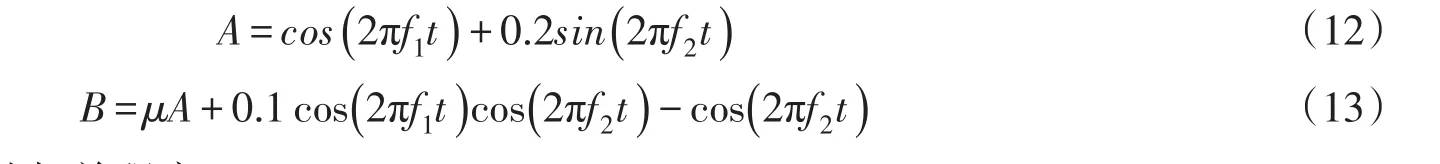
式中，μ代表两个信号之间的相关程度。

由式（12）和式（13）可以看出，时域信号B不仅包含时域信号A的信息，还包括自身的信息。因此，可以通过改变相关参数达到验证传递熵特性的目的。

3.1传递熵的不对称性和对相关程度的敏感性分析信号A、B的相关程度μ分别取0.2、0.4、0.8，计算模拟信号间不同方向的传递熵和，绘制不同相关程度的模拟信号间不同方向的传递熵随时间延迟的变化曲线，见图1。

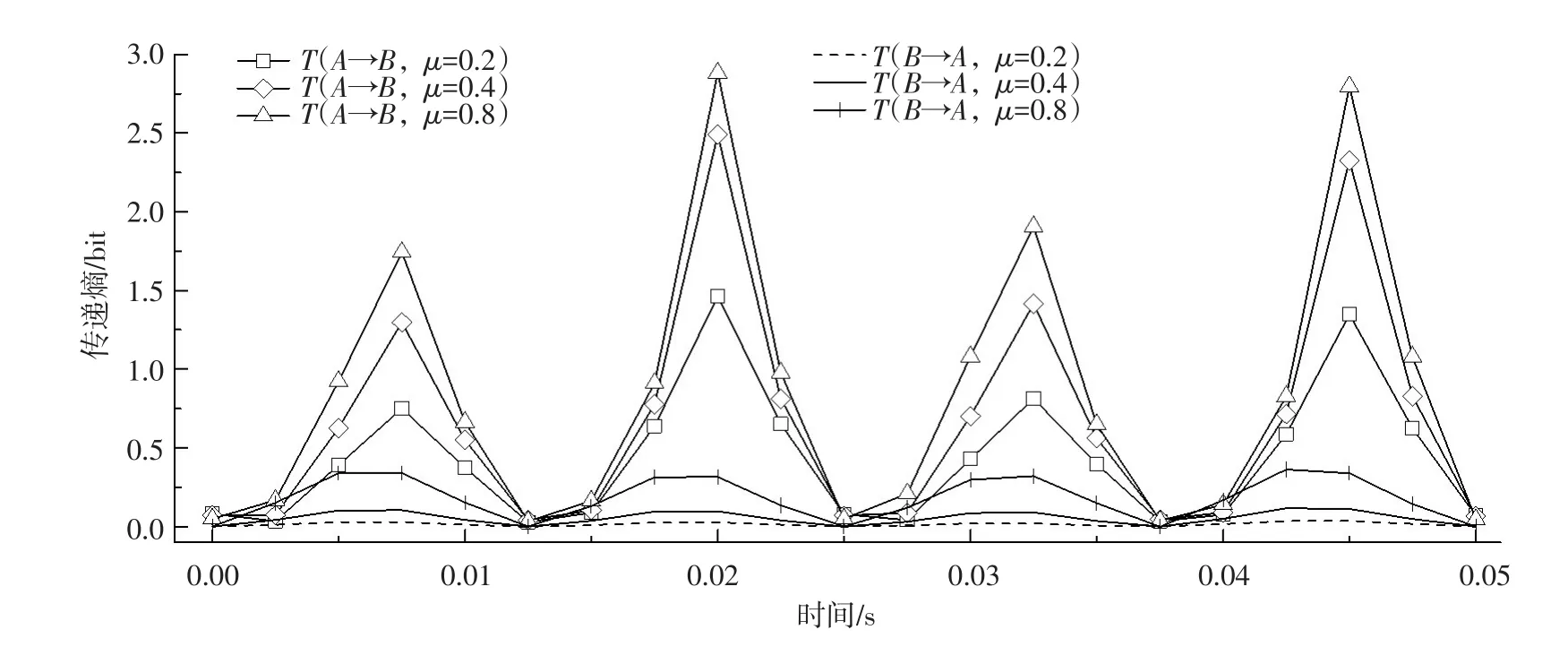
图1　模拟信号间不同方向的传递熵随延迟时间的变化曲线

由此可见，传递熵不仅可以反映信息传递间的方向性，也可以很好地度量两个信号之间的相关程度，证明了该计算模型的合理性和有效性。

3.2噪声对传递熵的影响信号A、B的相关程度μ取0.5，在信号A、B中分别加入高斯白噪声，分析噪声对传递熵大小和特征的影响。图3是加噪信号和不加噪信号间不同方向的传递熵随时间延迟的变化曲线。

从图3可以看出，T（A→B，加噪声）的传递熵值远小于T（A→B，无噪声）的值，说明传递熵的值受噪声的影响较大；T（B→A，加噪声）的值稍小于T（B→A，无噪声）的值，说明传递熵的值受噪声的影响相对较小。噪声的存在使得信息的状态发生变化，因此两个过程的信息流概率分布发生变化。但是，通过不同方向的传递熵幅值大小可得出不加噪声信号和加噪信号的信息传递方向均是A→B。因此，尽管噪声的存在影响不同方向传递熵的大小，但噪声的存在并不改变传递熵描述信息传递方向的有效性。

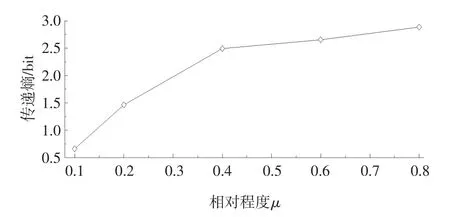
图2　最大传递熵峰值点（t=0.02s）处传递熵TA→B与时域信号相关程度的关系

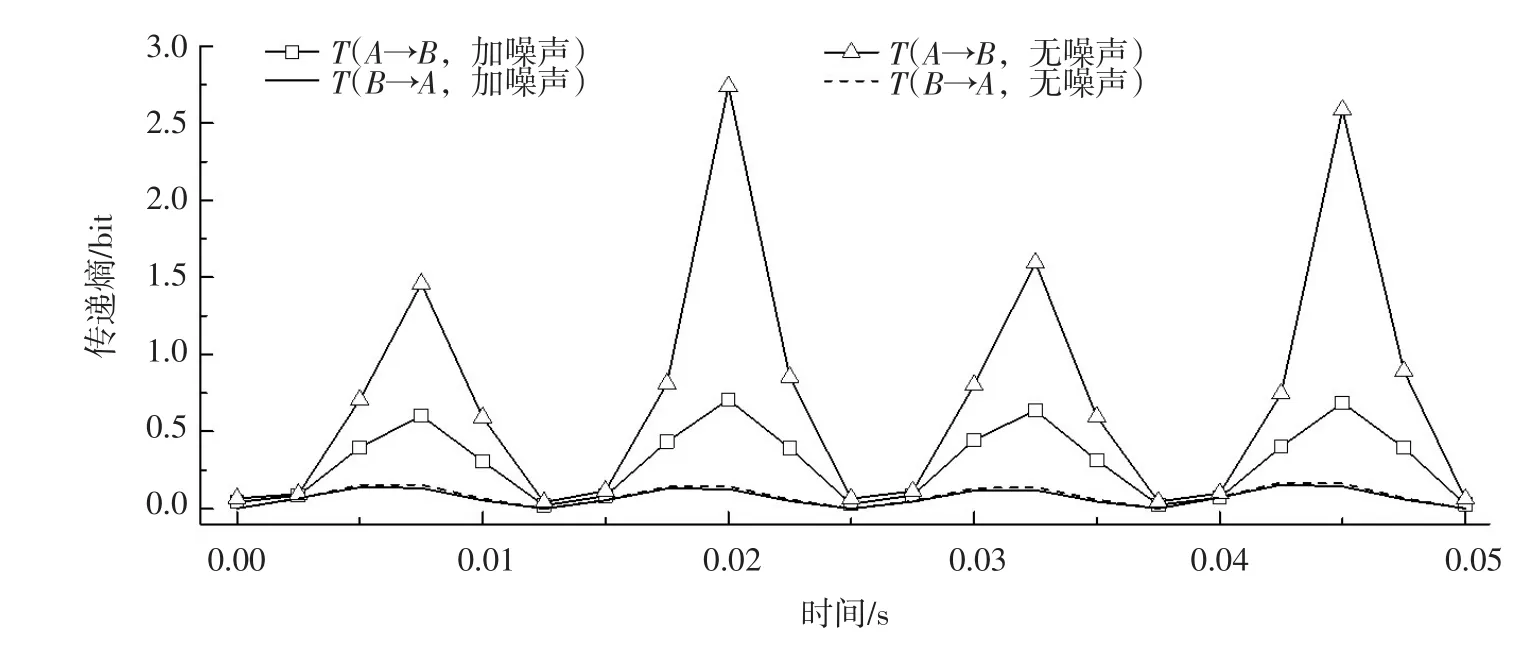
图3　传递熵随延迟时间的变化曲线（含噪信号）

4　水电站厂房结构振动传递路径分析

选取一大型水电站地下厂房机组为研究对象，现场监测采用DP型地震式低频振动位移传感器和INV多功能智能采集系统（含抗混滤波器），采样频率为400 Hz，采样时间为60 s，水轮发电机组额定功率为600 MW，导叶开度为42.2%，机组转速为100 r/min。INV多功能智能采集系统通道编号和测点位置的对应关系为：CH2—顶盖，CH4—定子基础，CH8—下机架基础，CH15—发电机层楼板。机组和厂房结构测点布置见图4。测试信号为实时功率为250 MW时各测点垂向振动位移值。该电站在部分负荷（30%～50%额定功率）范围内出现较强的涡带脉动，且顶盖测点垂向振动与尾水管进口、尾水管出口水压脉动具有良好的同步性［21］，低频尾水涡带脉动会在水轮机流道中向上传播，引起顶盖下相同频率成分的压力脉动［22］，因此顶盖测点在一定程度上可以表征尾水管中水流紊动情况，定子基础和下机架基础测点用于表征机墩部位振动情况，发电机层楼板测点用于表征电站厂房上部楼板结构振动情况。

4.1基于EMD的小波熵自适应阈值去噪效果分析水电站厂房振动测试过程中往往受到环境噪声影响，噪声的存在会影响信号的状态，进而影响传递熵的计算结果。因此在进行振源传递路径识别之前有必要对实测振动信号进行去噪，提高其信噪比，降低噪声对传递路径识别的影响。

首先对现场实测振动信号进行基于EMD的小波熵自适应阈值去噪。为了显示该去噪方法的有效性，分别采取软阈值去噪、EMD去噪和基于EMD的小波熵阈值去噪对机组定子基础垂向振动位移信号（图5）进行去噪，通过信噪比（SNR）对去噪效果进行评价。SNR的数学表达式如下：

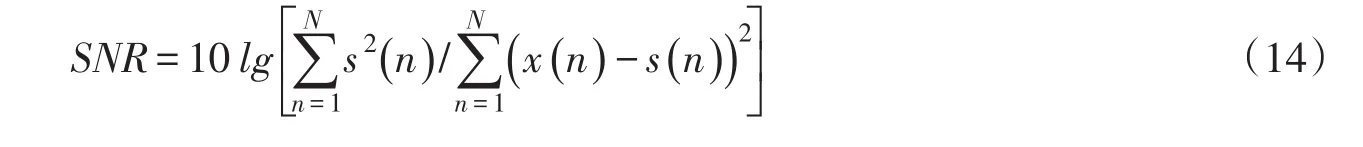
式中：x(n)为原始含噪信号，s(n)为去噪后的信号。表1列出了上述3种去噪方法的信噪比。

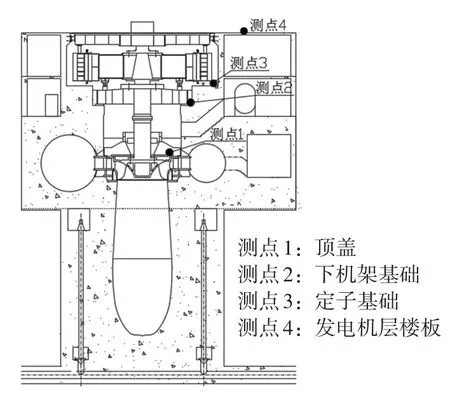
图4　机组和厂房结构测点布置图

表1　定子基础垂向振动信号不同去噪方法性能指标比较

由表1可以看出，基于EMD的小波熵自适应阈值方法去噪后的信噪比高于其它两个去噪方法，可见基于EMD的小波熵自适应阈值去噪方法可以较好地去除实测振动信号中的噪声，为后续的传递熵计算提供相对纯净的振动信号；信噪比达到10db以后传递熵受噪声的影响较小［23］。因此可以直接使用去噪后的信号进行传递熵计算。

4.2尾水涡带信号垂向传递路径分析水电站厂房的振源有机械振源、电磁振源、水力振源，其中影响最大的是水力振源，水力振源中的尾水涡带引起的振动具有波动周期长、传递路径远、影响范围大的特点，且尾水涡带作用于转轮、顶盖、尾水管等结构，是水轮机功率摆动、机组转动部分和尾水管壁低频振动、噪音的主要根源。因此尾水涡带对水电站厂房结构影响较大。本文基于机组和厂房结构原型观测垂向振动位移数据，主要研究尾水涡带（机组功率250 MW时）的垂向传递路径，分析其垂向传递规律；结合理论振源计算和实测振源分析可知尾水涡带对应的频带范围是0.2～1.3 Hz。

由于振动位移传感器量程原因，首先利用Matlab设计滤波器滤除0～0.2 Hz之间的信息，其次使用基于EMD的小波熵自适应阈值方法对原始信号进行去噪，然后采用db6小波基函数对振动信号进行小波8层分解，将尾水涡带对应频带的小波系数进行重构获取尾水涡带信号，最后用传递熵方法对测点间的尾水涡带信号进行垂向振动传递路径识别。对振动信号进行小波分解后各频段的频率范围见表2，其中b1～b8和a8对应为信号小波分解后的从高频到低频相应层信号。将a8和b8对应的重构信号作为尾水涡带信号引起的垂向振动位移分量。水电站厂房振动测试信号和重构得到的尾水涡带信号可近似看作各态历经的、高斯的时间序列。因此可以直接利用简化的传递熵公式对水电站厂房尾水涡带信号进行传递路径分析。尾水涡带在两个不同测点之间不同方向的传递熵随时间延迟的变化曲线见图6。

根据不同方向传递熵的幅值大小关系，由图6（a）可以看出：除了时间点t=0以及时间延滞点t=0.65 s附近之外，T（2→4）的传递熵值远远大于T（4→2），说明由顶盖流向定子基础的信息量远远大于相反方向，可以判断尾水涡带信号由顶盖传至定子基础；同理根据T（2→8）和T（8→2）的关系可以判断尾水涡带信号由顶盖传至下机架基础。由图6（b）可以看出：除了时间点t=0以及时间延滞点t=0.65 s附近之外，T（4→15）的值远远大于T（15→4），说明由定子基础流向发电机层楼板的信息量远远大于相反方向，可以判断尾水涡带信号由定子基础传至发电机层楼板；同理根据T（8→15）和T（15→8）的关系可以判断尾水涡带信号由下机架基础传至发电机层楼板。

为了说明尾水涡带的垂向传递路径，在此基础上还需对不同测点的传递熵综合分析。根据以上多组两个测点之间的信息传递关系，可以得出尾水涡带的两条垂向传递路径：尾水涡带引起的垂向振动从顶盖传至定子基础，然后由定子基础传至发电机层楼板；尾水涡带引起的振动从顶盖传至下机架基础，然后由下机架基础传至发电机层楼板。结合水电站机组与厂房的结构特点可知：由于顶盖与水流直接接触，尾水管水流脉动在顶盖位置的振动中可以很好地反映出来，尾水涡带引起的垂向振动通过顶盖传至机墩（定子基础、下机架基础）；由于风罩底部与机墩环向连接，顶部与发电机层楼板整体连接，因此尾水涡带引起的垂向振动通过风罩从机墩（定子基础、下机架基础）向发电机层楼板传递。

表2　振动信号小波分解后各频段的频率范围

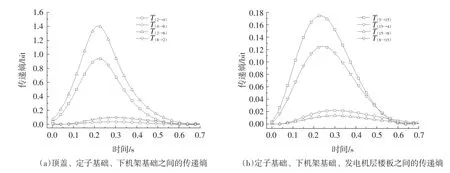
图6　尾水涡带在不同测点之间的传递熵随时间延迟的变化曲线

4.3信息传递率为了定量描述信号间的能量传递关系，在传递熵的基础上提出了信息传递率的概念［23-24］。对于两个平稳的马尔可夫过程x和y，基于传递熵的信息传递率为：为23.5%和16.1%，可见机墩（定子基础、下机架基础）到发电机层楼板的传递率相对较低，主要是风罩、梁柱、上下游挡墙等部位起到了一定的消能减振作用。

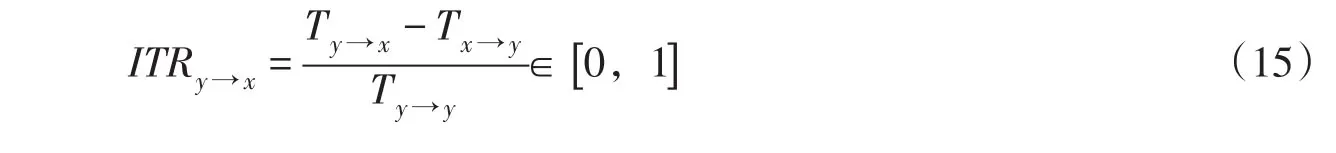
表3　不同相关程度下A、B之间的相关系数和ITRA→B

表4　不同测点之间的信息传递率

5　结论

提出了基于传递熵的水电站厂房振动传递路径识别方法，为了降低噪声对路径识别的影响，首先使用基于EMD的小波熵自适应阈值去噪方法对实测振动信号进行去噪，然后通过对模拟信号的分析证明了传递熵方法的有效性。

以一大型水电站为研究对象，通过小波分解和重构得到尾水涡带信号，利用传递熵理论对尾水涡带信号进行分析可以得到尾水涡带在机组功率为250 MW时的垂向传递路径是：尾水管→机墩（定子基础、下机架基础）→发电机层楼板。为了定量描述信号的动态特征变化，提出了基于传递熵的信息传递率的概念，信息传递率可以定量描述水电站厂房结构不同测点之间的能量信息传递特征。

本文的研究为分析水电站厂房振动振源的传递路径提供了一种新的思路，基于传递熵进行传递路径识别的方法具有判断逻辑简单的特点。论文的工作着重于传递熵方法的适用性上，需要在此基础上进行算法的优化，对于传递熵在不同传递路径对单点振动的贡献率、主次要传递路径的识别等方面的应用还有待进一步深入研究。