边坡倾倒稳定分析的矢量计算

董正中,雷永刚,白雪亮

(中国电建集团西北勘测设计研究院有限公司,西安 710065)

0 前 言

倾倒破坏是反倾岩质边坡失稳的主要模式，常发生于走向与边坡平行但倾向相反的层状岩体中。当岩体中发育有顺坡向的节理或裂隙时该破坏形式更容易发生[1-2]。极限平衡分析仍是目前最为常用的一种方法。Goodman和Bray(1976)最早提出了分析倾倒稳定的极限平衡法[3]，这一方法将滑坡体用反倾向的结构面切割成多个宽度为ΔL的条块，对于任一条块，作用其上的力使得该条块处于以下3种状态的一种：① 稳定；② 倾倒破坏；③ 滑动。处于不同状态的条块将滑坡体分成立稳定区、倾倒区和滑动区3部分，如图1所示。这种计算方法经过多名学者做了改进，包括：将矩形条块推广到平行四边形；考虑条块底部岩桥作用等[4-5]。本文通过矢量运算计算分析条块倾倒稳定安全系数，使条块的顶面和底面适应任意形状，并提出了倾倒条块分析时条块底部岩桥应力三角形分布规律。

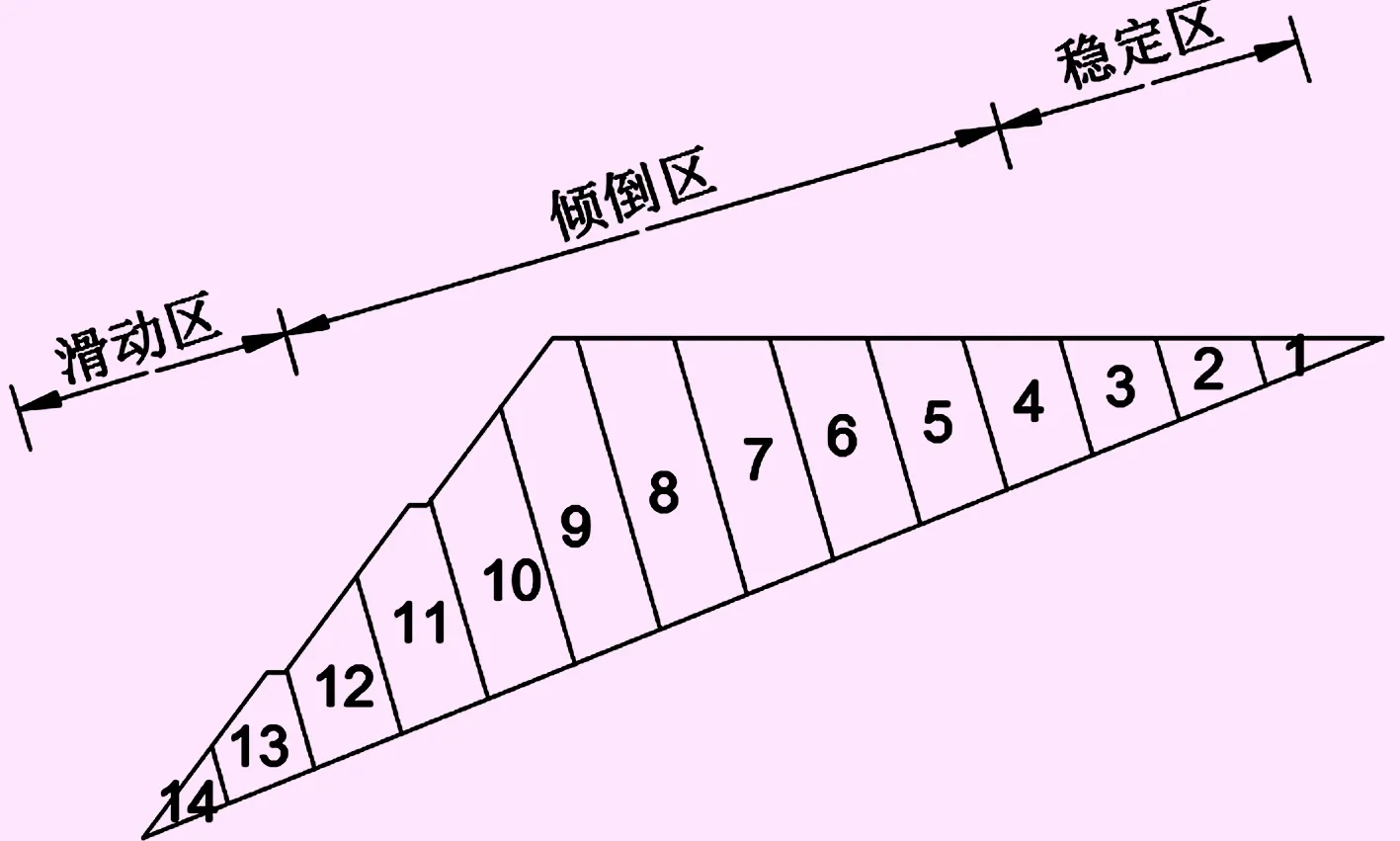
图1 倾倒边坡的典型结构特征图

1 基本原理和安全系数计算方法

从坡顶开始对每个条块进行计算，分别通过滑动稳定分析求出每个条块左侧的推力Pl.s，和倾倒稳定分析求出每个条块左侧的推力Pl.t(滑动条块和倾倒条块受力分析见图2、3)，则保持条块稳定所需的力Pl=max(Pl.s,Pl.t)。若Pl<0则该条块为稳定块；若Pl>0且Pl=Pl.s则该条块为倾倒块，若Pl>0且Pl=Pl.t则该条块为倾倒块。从坡顶第一个条块一直算到坡脚最后一个条块，最后一个条块左侧保持稳定所需的力为P0，P0即为边坡的剩余推力，当P0>0时，边坡处于失稳状态，当P0=0时，边坡处于极限平衡状态，当P0<0时，边坡处于稳定状态[3]。

定义倾倒稳定分析的安全系数为F[4]。 为条块的实际力学参数(反倾岩层摩擦角φs.0、底面顺坡摩擦角φb.0、底滑面粘聚强度c0、底面岩桥抗拉强度σt.0)与每次试算时条块的力学参数(φs、φb、c、σt)的比值，即每次试算时φs=φs.0/F,φb=φb.0/F,c=c0/F,σt=σt.0/F。不断地变化F值，试算边坡的剩余推力P0。当P0=0时的F即为倾倒稳定的安全系数。

2 条块分析

根据边坡表面(天然地形面或人工开挖面)，反倾岩层倾角及厚度，底面顺坡向的节理裂隙的倾角，通过几何运算计算出所有条块的数量，包括每个条块的每个顶点坐标值。以下针对某一个条块分别进行滑动分析和倾倒分析。

2.1 滑动条块分析

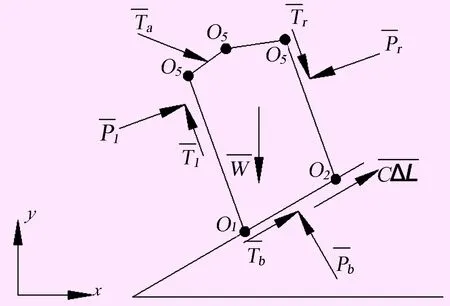
图2 滑动条块受力分析图

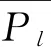
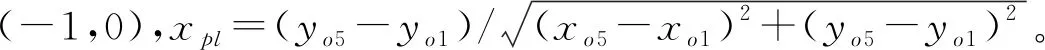
力的标量中Pl和Pb是未知量，其他力的标量都是已知量，通过x和y方向力的平衡可以得出下面公式(1)：

M1Pl+M2Pb+M3=0

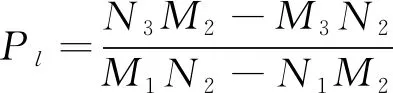
(1)

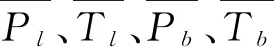
M1=xpl+tanφsxTl

M2=xpb+tanφbxTb

N1=ypl+tanφsyTl

N2=ypb+tanφbyTb

(2)

2.2 倾倒条块分析

某个条块滑动受力分析如图3所示，σt为岩桥底面抗拉强度，ξΔL是岩桥底面长度，oH是倾倒点o1到锚固力矢量的垂足坐标，oH=(xoH,yoH)，其他参数意义同图2。

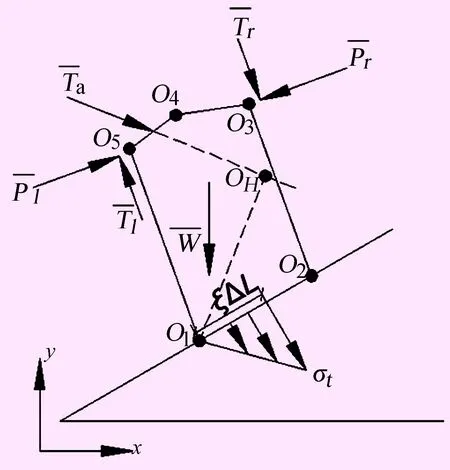
图3 倾倒条块受力分析图

通过岩桥底面长度控制底滑面是否完全连通，本文假定岩桥在底滑面的左侧。当条块即将发生绕倾倒点o1的倾倒变形时，岩桥底面远离点o1变形逐渐增大，最远处应力首先达到抗拉强度σt，极限平衡时底面拉应力的三角形分布规律如图3。这样的假设可以保证底滑面不完全连通时的安全系数永远大于完全连通的安全系数，与实际规律相符。

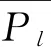
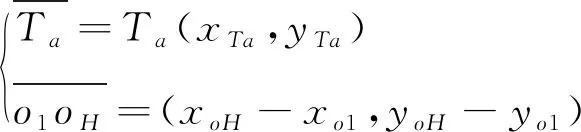
MTa=Ta[xTa(yoH-yo1)-(xoH-xo1)yTa]

(3)

3 计算实例

通过编程实现了上述计算过程。只需导入边坡地形数据，水面线数据，然后简单地输入岩层倾角及厚度，底滑面倾角，锚固参数，以及条块物理力学参数等，就可自动实现倾倒稳定安全系数的计算，并实现计算图形绘制。

以Hoek[7]等提供的算例为例。开挖边坡高92.5 m，坡脚为56.6°，坡顶面仰角为4°，岩层反倾倾角为60°，倾向坡内，底滑面倾角30°。岩体容重γ=25 kN/m3，条块底面和侧面的摩擦角φ均为38.15°。将破坏岩体分为16个岩块。分别按以下4个计算条件计算，程序生成的计算图形见图4～7，安全系数见表1。

表1 各计算条件下的安全系数表

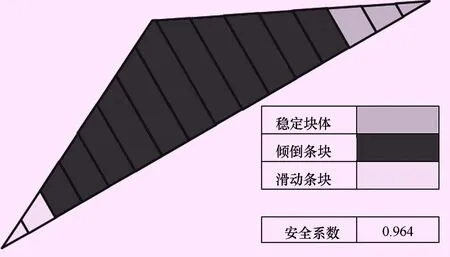
图4 条件(1)程序计算图形

图5 条件(2)程序计算图形

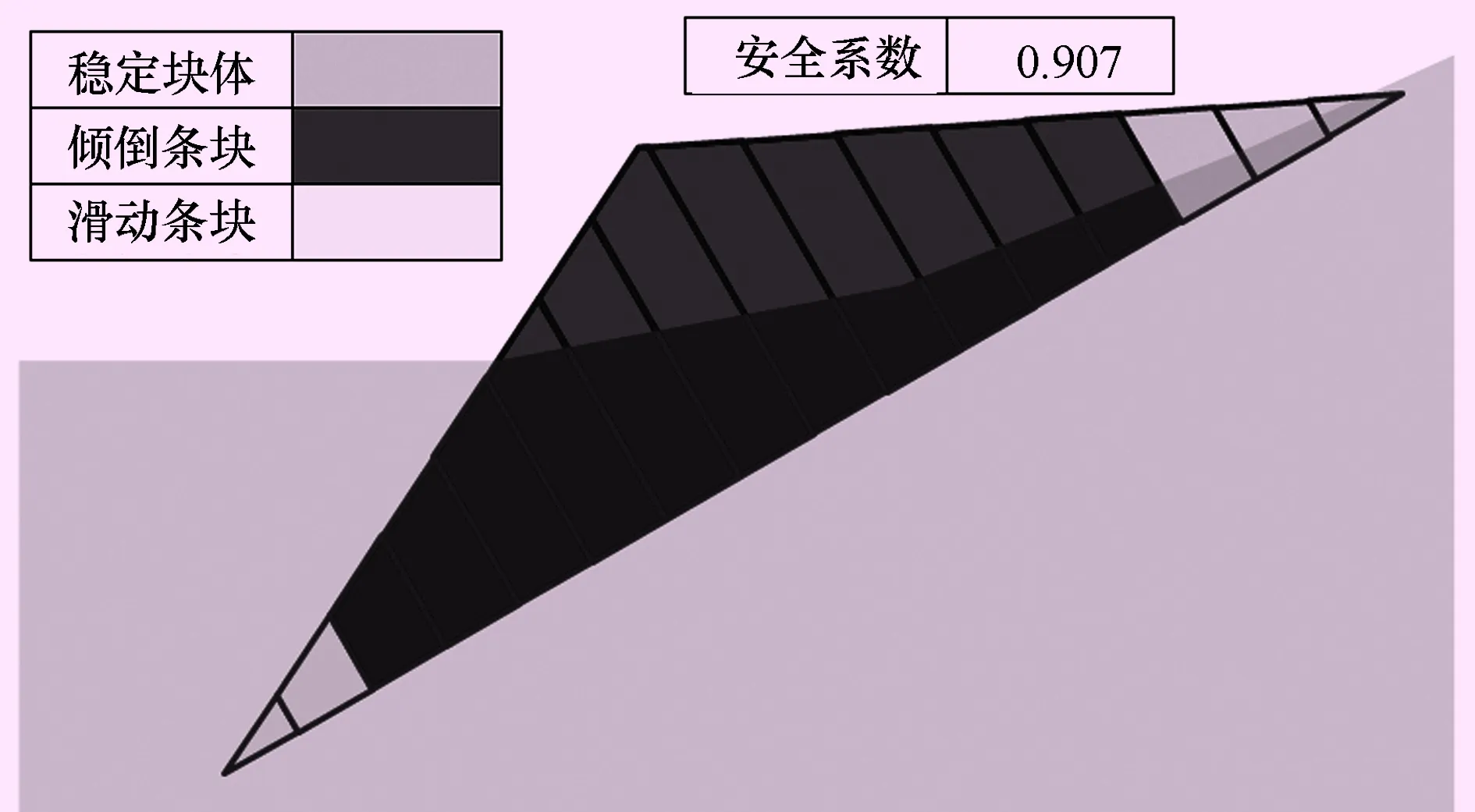
图6 条件(3)程序计算图形

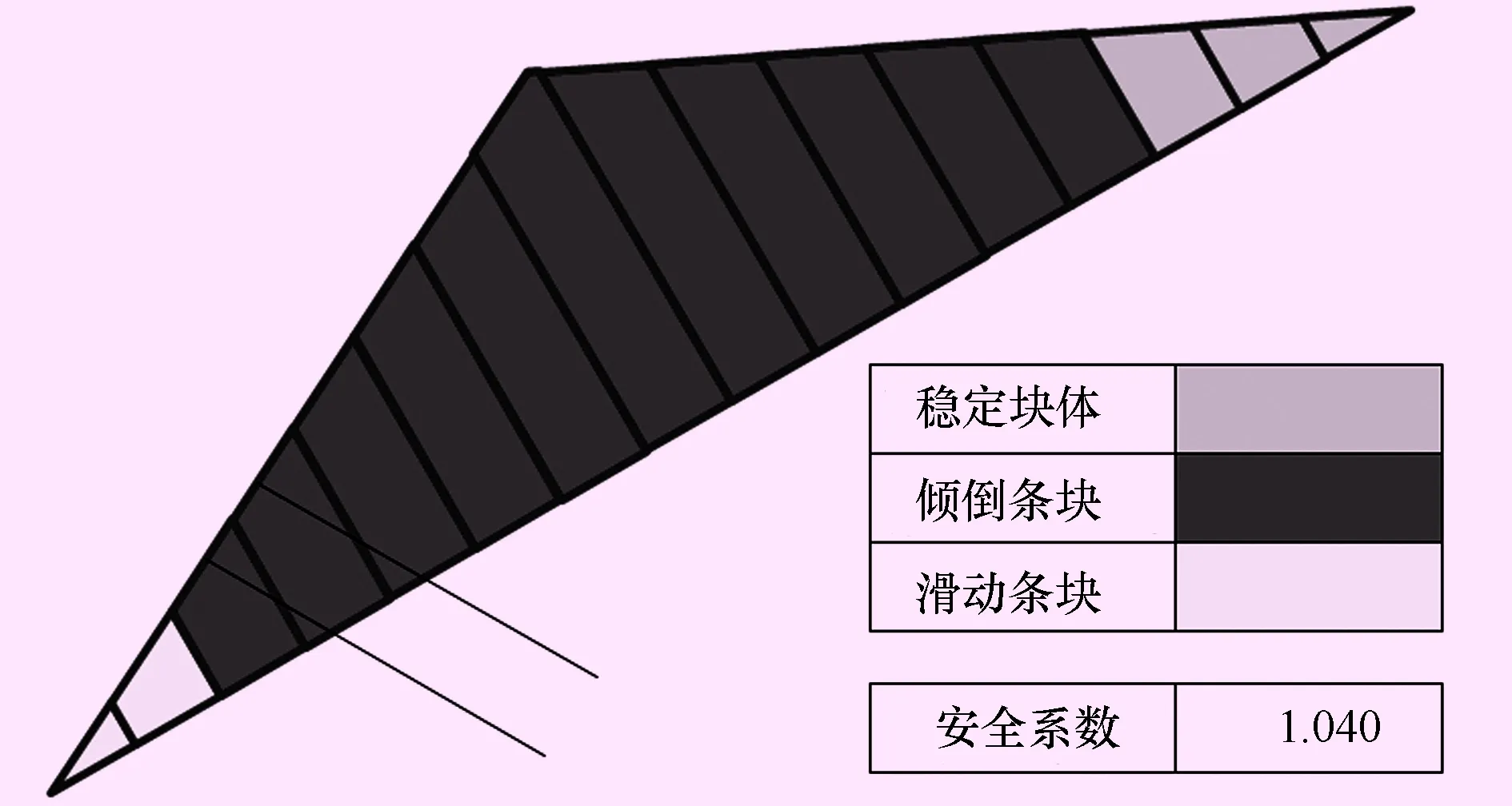
图7 条件(4)程序计算图形

计算条件(1)：底滑面完全连通。

计算条件(2)：底滑面考虑40%连通率，岩桥底面抗拉强度1.5 MPa。

计算条件(3)：底滑面完全连通，考虑一定的地下水位分布。

计算条件(4)：底滑面完全连通，分别在高程30 m和40 m处，加2根锚索，锚固角30°，张拉均为吨位100 t。

从计算结果看出：计算条件(1)与Hoek算例的结果“边坡处于极限平衡状态”基本一致，Hoek算例中，每个条块被简化为矩形，本文的计算程序无需简化，每个条块形状与实际形状一致；计算条件(2)在考虑条块底滑面不完全连通后，安全系数有了实质的提升，且倾倒条块的数量有所减少；计算条件(3)表明地下水位对倾倒稳定不利；计算条件(4)安全系数较不锚固的情况有所提高。

4 结 论

(1) 本文计算方法适用于反倾岩质边坡倾倒失稳破坏，可考虑任意边坡表面以及折线底滑面，并可计算水压力、锚固力、地震惯性力等相关荷载作用。

(2) 根据改进的Goodman-Bray方法通过矢量计算稳定安全系数，考虑了底滑面不完全连通的因素，并提出了底滑面岩桥的应力三角形分布规律。

(3) 本文的计算方法中，各条块形状无需是矩形或者简化为平行四边形，顶面和底面与实际条块形状一致。

(4) 采用矢量计算倾倒稳定安全系数，计算公式比较简洁、统一、利于编程实现，且在其它各种工况条件下荷载的添加比较容易实现。

(5) 在采用矢量计算分析滑动条块力的平衡时不必判断各种荷载的正负号，分析倾倒条块力矩平衡时也无需判断各种荷载产生的是倾覆力矩还是抗倾力矩。