高聚物锚固体与土体黏结特征试验与数值模拟

刘　恒，王复明，石明生

（郑州大学 水利与环境学院，河南 郑州　450001）

1　研究背景

随着国内外基础设施建设的高速发展，锚杆在隧道工程、地下工程和边坡防护等工程领域得到了广泛的应用［1］。由于锚杆工作的岩土环境复杂多样，以水泥砂浆为代表的传统锚固材料在固化过程中易干缩开裂，导致锚杆强度降低或因杆体锈蚀而过早失效，从而影响锚固工程的稳定。现阶段对于锚固材料的改良，大多是在水泥砂浆中添加改性剂，减少水泥基锚固体的干缩现象，虽说也取得了一系列的成功应用［2-4］，但此类改良并未改变有水参与反应的本质，因此锚固性能提升有限。

具有自膨胀特性的高聚物是将双组份液态聚氨酯通过注浆设备在一定压力和温度下反应生成的固化物，是一种优良的锚固材料，其主要特点为：（1）高聚物材料在固化过程中体积膨胀，可完全充满钻孔，有利于增大锚固体与基体间的作用力；（2）高聚物材料不透水［5］，对钢制杆体而言是隔水材料，可以防止杆体锈蚀，提高耐久性；（3）高聚物材料弹性较好，能够和土体协调变形，抗拉强度高，不易开裂；（4）高聚物材料的固化时间为15～30 s，并无需养护［6-7］，因此有利于缩短施工工期；（5）高聚物材料固化过程中完全没有水参与反应，注浆设备需要的工作面小，尤其适用于湿陷性黄土、膨胀土以及各类应急抢险锚固支护工程。石明生等［8］曾在工程现场以高聚物为锚固材料，开展锚杆拉拔试验，并将常规水泥砂浆锚固材料设置为对比组，发现高聚物和土体间具有更大的黏结力，施工后即可提供强度，证实了高聚物锚固材料的经济性和高效性。随后，石明生等［9-10］在粉土中开展了高聚物锚固试验，研究高聚物密度、钻孔孔径等因素对高聚物-土体黏结强度的影响。但是，目前高聚物锚固体和土体相互作用机理仍然不清楚，界面黏结强度参数也不完善。本文在上述研究的基础上，采用大比尺模型试验测试高聚物锚固体与不同状态土体的黏结强度值，为高聚物锚固注浆设计及应用提供数据支持，并利用颗粒流软件，从细观角度分析土体应力分布、传递特征以及孔隙率变化的特征。

2　高聚物锚固体与土体黏结试验

2.1试验过程采用大比尺模型开展高聚物锚固体的拉拔试验，试验装置如图1所示。大型击实筒为壁厚12 mm、内径800 mm、高1 000 mm的钢桶，用于击实土体并提供侧限。击实筒中央布置外径100 mm、长900 mm钢管，用于锚杆孔的成型（图1（a））。

试验前对螺纹钢筋进行除锈，并焊接对中支架，支架的作用是确保杆体居中并增大杆体和高聚物锚固体间的作用力。在钢筋上冲切2个对称的深3 mm、宽6 mm的凹槽，将7个耐高温（高聚物固化温度大于150℃）应变片交替粘贴到凹槽中，应变片间距10 cm。随后，在大型击实筒中填土，取土场地原位土层参数如表1所示。采用10 kg轻型锤自由落体的方法进行分层击实，每层填土分别测试含水量和密度，用于计算并判定其物理状态。填土击实完成后，抽出钢管，形成锚杆孔。在孔中植入钢筋及注浆管，植入方式如图1（b）所示。注浆管有2根，分别用于封孔注浆和锚固注浆［11］，短管为封孔注浆管，管底在封孔布袋中，向布袋中注入适量高聚物浆液，布袋膨胀把孔口封闭。封孔的目的是防止高聚物自膨胀时从孔口溢出，确保高聚物材料在固定的空间内完成硬化，达到控制高聚物密度的目的。本文试验设计高聚物锚固体密度0.12 g/cm3，封孔高聚物密度0.2 g/cm3。封孔注浆完成后，进行锚固注浆，注浆完成20 min内即进行拉拔试验。

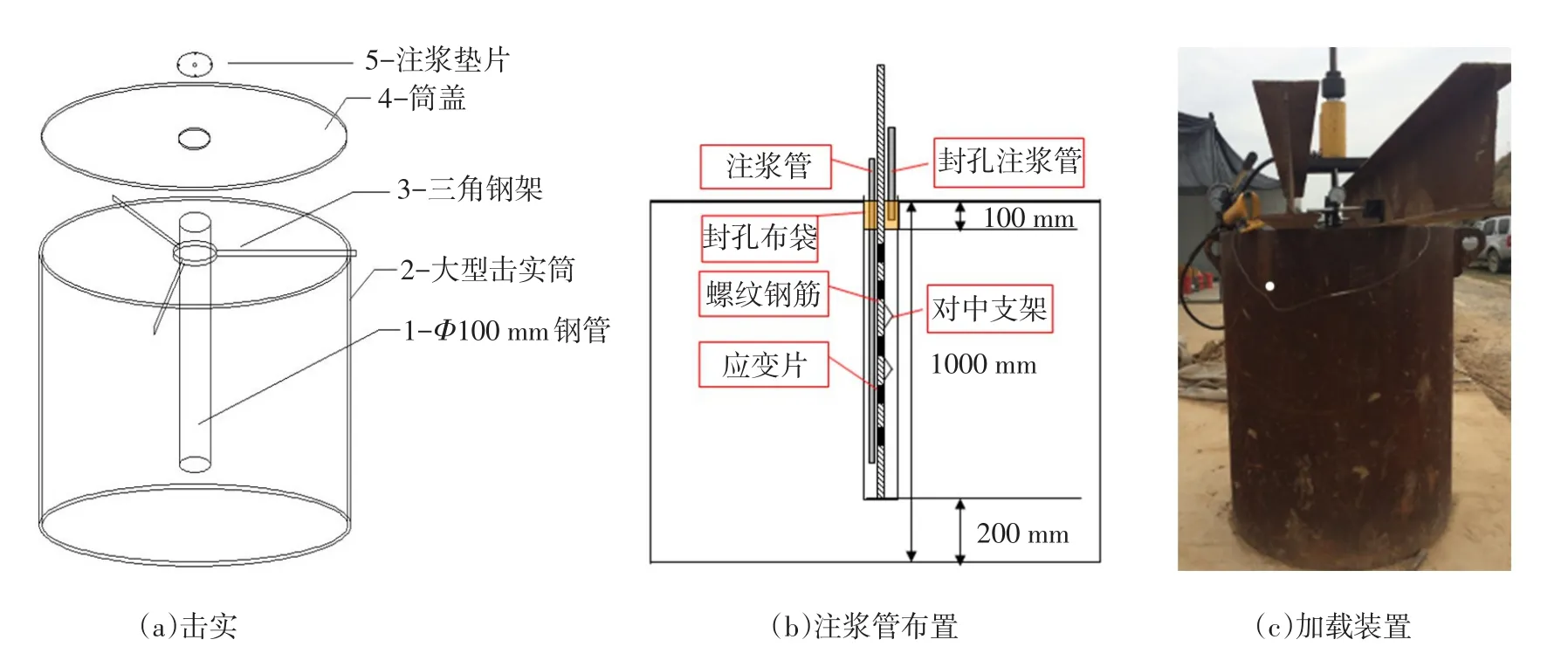
图1　试验装置

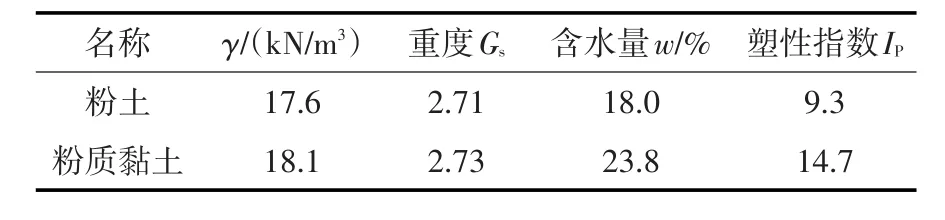
表1　试验土样物理性质指标

试验时，采用液压千斤顶加反力框架分级加载（图1（c）），将应变片导线接入CM-2B应变测试系统采集锚杆应变。本文试验主要研究高聚物锚固体与土体的相互作用，加载前将封孔段挖除，有效锚固长度为70 cm。加载分级数由加载端位移控制，在某级荷载下，如果位移稳定，则继续加载；若位移不收敛且持续增加，则停止加载。

本文试验填筑不同状态土体共19组，锚固体系的破坏形式均为锚固体被拔出，钢筋和锚固体间未产生相对位移。拉拔荷载作用下，无论是粉土层还是粉质黏土层，均出现孔口周围填土隆起的现象，卸载后回弹，说明填土随高聚物锚固体向上移动，孔口附近土体位移较大；粉土表面产生大量径向裂纹，土体边缘环向开裂，形成锥形破坏面。本文19组试验中高聚物注浆量相同，试验完成后将高聚物锚固体取出，分别在其上、中、下不同位置采样测试高聚物密度，结果显示锚固体密度下部大上部小，整体上相对均匀，为0.115～0.128 g/cm3，平均密度约为0.12 g/cm3，接近设计值。

2.2试验结果分析

2.2.1低密度高聚物锚固体与不同状态土体黏结强度本文试验获得的不同状态土体与高聚物锚固体的界面黏结强度如表2所示。

表2　不同状态土体与锚固体黏结强度

由于试验土层为重塑土，土体结构性遭到破坏，且容易受含水量的影响，试验得出的界面黏结强度略小于实测值（中密度粉土与密度为0.12 g/cm3高聚物锚固体黏结强度现场测试值为80～140 kPa）。

2.2.2拉拔荷载-位移关系曲线试验得出的锚杆加载端荷载-位移曲线如图2、图3所示，从图中可以看出，在分级加载条件下，粉土层和粉质黏土层锚杆加载端荷载-位移曲线的变化都可分为三个阶段：加载初期（OA段），曲线近似直线段，此时土体和高聚物材料黏结较好，锚固界面处于弹性阶段；随着荷载的增大（AB段），曲线为渐变曲线，其斜率逐渐减小，锚固界面进入弹塑性变形阶段，部分区域达到极限平衡状态，形成塑性区；随着荷载的继续增加（曲线BC段），高聚物材料和土体截面脱黏并产生相对滑移，此时锚杆抗力主要是高聚物材料和土体界面摩擦力，荷载增量较小时位移增量就十分明显，荷载-位移曲线演化成近水平线，残余强度与峰值强度相当，几乎无界面软化现象。

加载端荷载-位移可以拟合为指数函数关系：

式中：a为极限拉拔荷载；b为衰减因子；u为加载端位移。

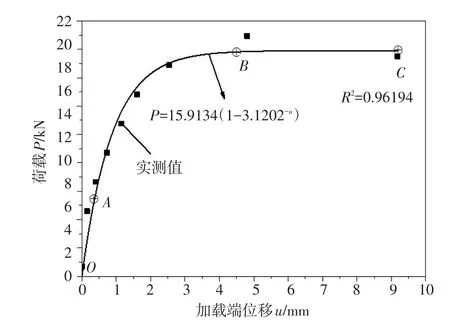
图2　粉土中加载端拉拔试验加载端荷载-位移曲线

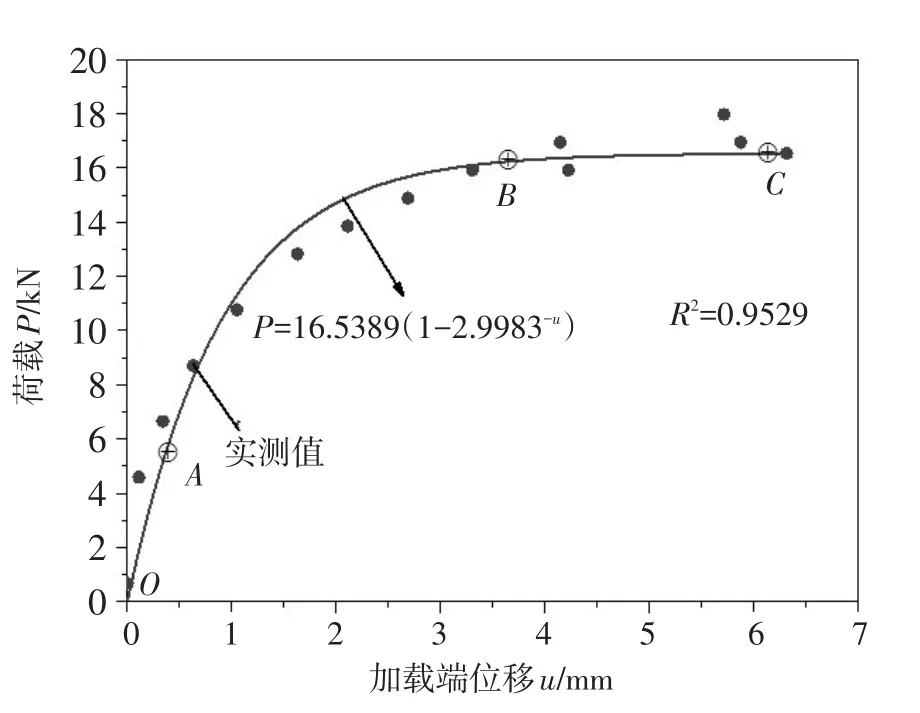
图3　粉质黏土中拉拔试验加载端荷载-位移曲线

2.2.3锚杆轴力和黏结应力分布根据锚杆各测点应变数据可计算得出锚杆轴力、锚固界面黏结应力沿锚固段的分布曲线，如图4所示。轴力从加载端到自由端逐渐减小，自由端轴力并不为0，约为加载端轴力值的8%。当荷载较小时（P=3.05kN），界面黏结应力由加载端向自由端递减；随着拉拔荷载的增大，界面黏结应力由加载端先急剧增大至峰值，又迅速衰减趋于稳定值，峰值点位于距加载端0.3 m处。本次试验未获得随着荷载增大，界面黏结应力峰值向自由端移动的现象，主要原因是模型试验锚杆长度较短，当加载端锚固界面产生开裂时，迅速扩展到自由端，锚固体和土体产生间的滑移相对较大。根据文献［12］的结论，锚杆弹性模量越大，锚固体弹性模量越小，则界面黏结应力集中程度也越小。图4也证实了这一点：由于高聚物弹性模量远小于水泥砂浆的弹性模量，因此相较于水泥砂浆锚固体，无论是钢筋轴力和锚固界面黏结应力，应力集中程度相对较小，锚固末端钢筋轴力和界面黏结应力并未趋近于0。

3　高聚物锚固体系的颗粒流数值模拟

3.1模型建立二维颗粒流程序（PFC2d）是一种采用离散单元法对细观颗粒介质运动及相互作用进行数值模拟的软件系统。与连续介质力学不同，颗粒运动不受变形协调的约束，只需满足平衡方程［13-14］。该方法通过微细观参数变化研究材料的宏观力学行为，克服了传统连续介质力学模型的宏观连续性假设，是目前研究岩土力学破坏机理问题的一种有效手段。

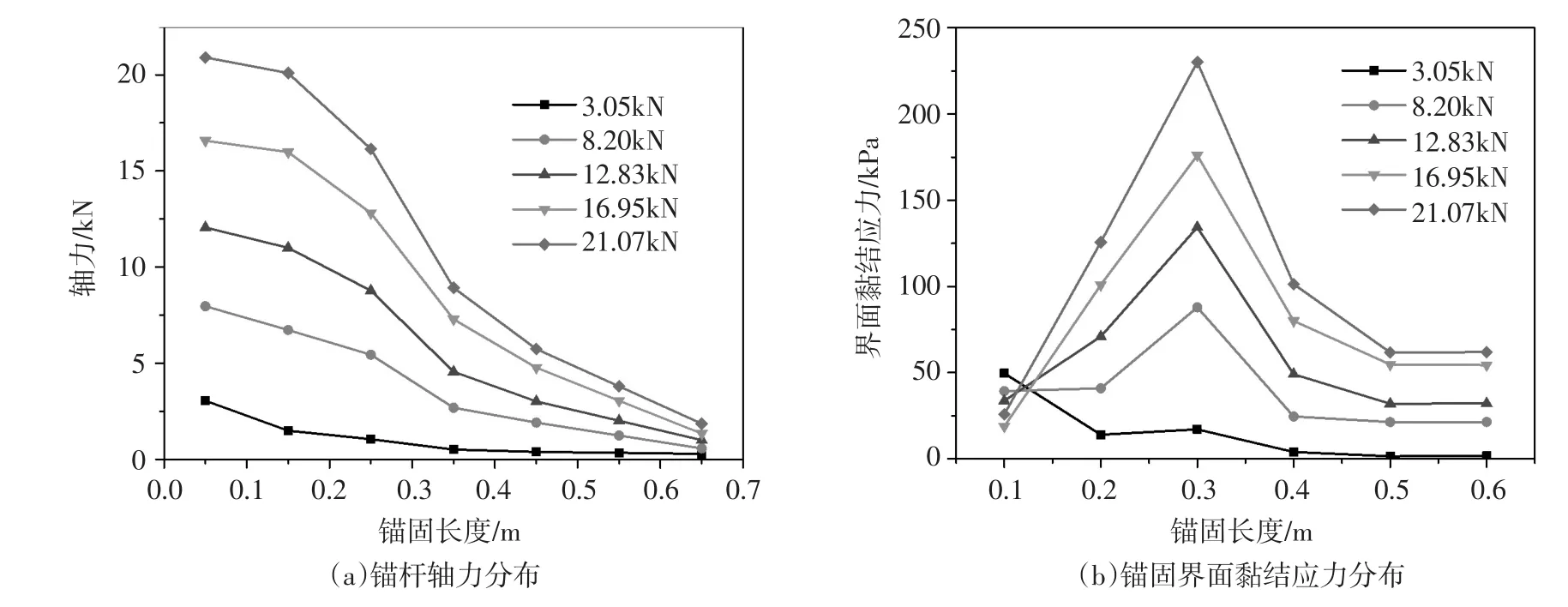
图4　各级荷载作用下锚杆轴力、锚固界面黏结应力分布

颗粒大小对PFC2d模型宏观特性有一定的敏感性，但如果最大直径和最小直径的比值选取得当，可以消除这种敏感性，因此没有必要采用精细的直径来模拟材料不是很精确的特性。对于较大的模型，颗粒数量太多，会超出计算机的运算能力，耗时且不经济。因此，模拟时采用量纲分析原理（即π定理）并结合相似性原理，将室内试验模型进行缩尺模拟，以达到减少计算量的目的［15］。为确定数值模型和试验模型的相似系数，选择以下参数建立方程：室内试验模型高H，锚固体直径B，重力加速度g，土中应力σ，土体位移S，土体重度γ，土体压缩模量E，锚固体长度L。可表示为：

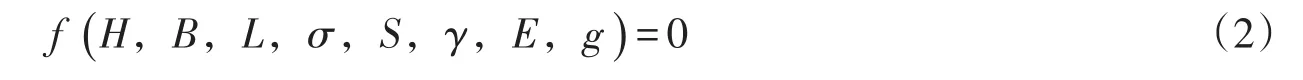
取相似系数Cg=10，则Cσ=CE=1，CS=CL=CB=CH=0.1，建立颗粒流数值模型如图5所示。

模型箱尺寸为100 mm×100 mm，锚杆杆体（钢筋）由17个半径为2 mm的颗粒组成，高聚物锚固体和土体颗粒同时生成，半径为0.24～0.75 mm，锚固体和土体有效接触长度为70 mm，与模型试验70 cm有效锚固长度对应。高聚物材料和土体的细观参数根据常规三轴试验结果进行标定，钢筋细观参数则根据拉伸试验进行标定，根据标定结果，高聚物材料和土体均取接触黏结模型，钢筋取平行黏结模型，各材料细观参数如表3所列。在土体颗粒中布置10行4列直径为10 mm的测量圈［15］，运算过程中用以记录土体中应力和孔隙率变化情况。

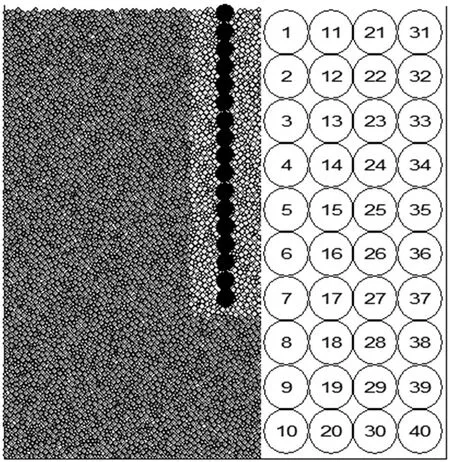
图5　颗粒流模型及测量圈布置

3.2极限荷载的确定模型平衡完成后，对锚杆顶端颗粒施加竖直向上的集中力，实现加载过程。运算时，定义锚杆径向为x方向，轴向为y方向。

在室内模型试验中，主要根据某级荷载下加载端位移情况判断锚杆是否发生黏结滑移。因此，在采用PFC2d模拟时，也根据加载端位移来确定极限荷载。在加载过程中，记录每一级上拔荷载作用下锚杆的位移与时步的关系。在某级荷载下，如果锚杆位移-时步曲线末端为近似水平线并趋于稳定（如图6（a）），则说明该级荷载下位移收敛，可施加下一级荷载；反之，如果曲线末端为向上倾斜（如图6（b）），则说明锚杆位移不再收敛，锚固体系有失稳趋势，取上一级荷载为极限荷载。经上述原理分析，最终确定张拉极限荷载为25 kN，每级荷载5 kN。模拟加载时，监测不平衡力大小以及锚杆端部位移来控制每级荷载下模型运行的步数，当不平衡力较小时位移才有可能稳定，此时方可施加下一级荷载。根据简化模型的运行结果，最终取每级荷载下循环4000步。

表3　土体、锚固体数值模型细观参数

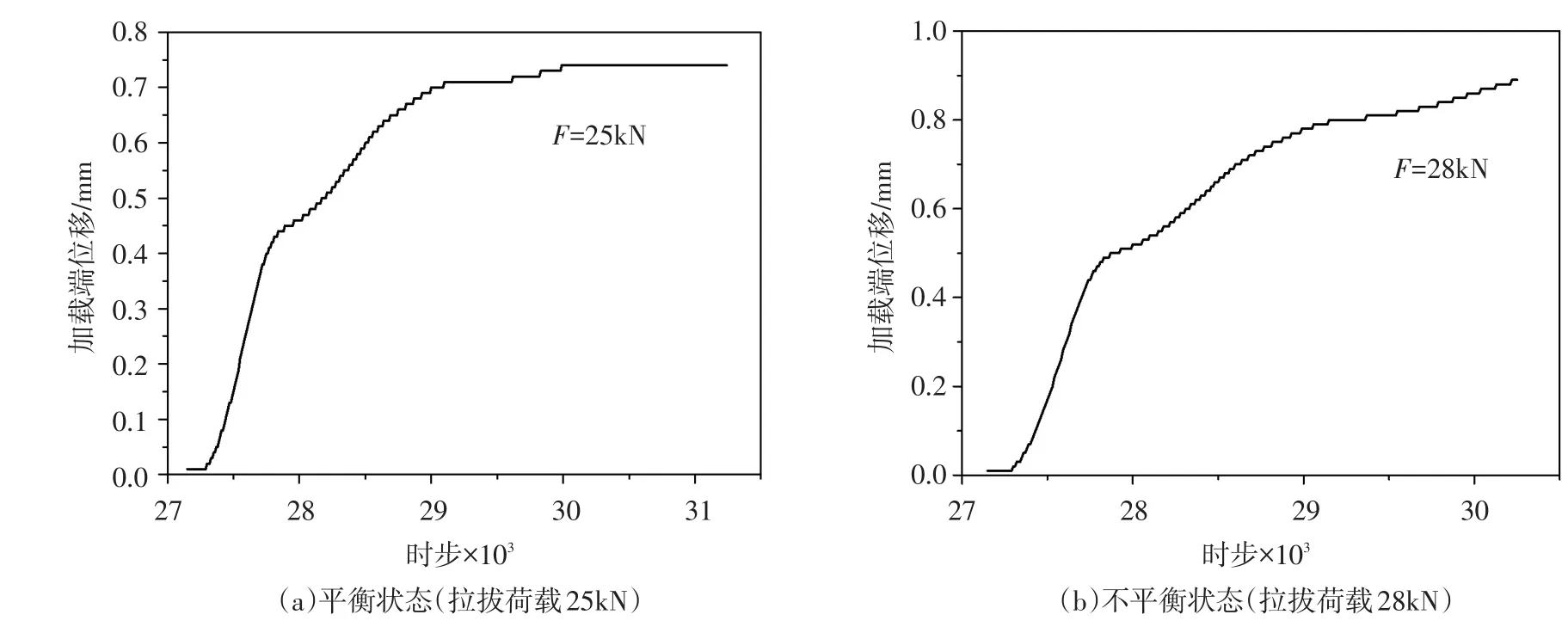
图6　不同荷载条件下加载端时步-位移曲线

3.3模拟结果分析

3.3.1土体应力分析图7为模型在15 kN拉拔荷载作用下达到平衡状态时，各测量圈y向应力的分布曲线。

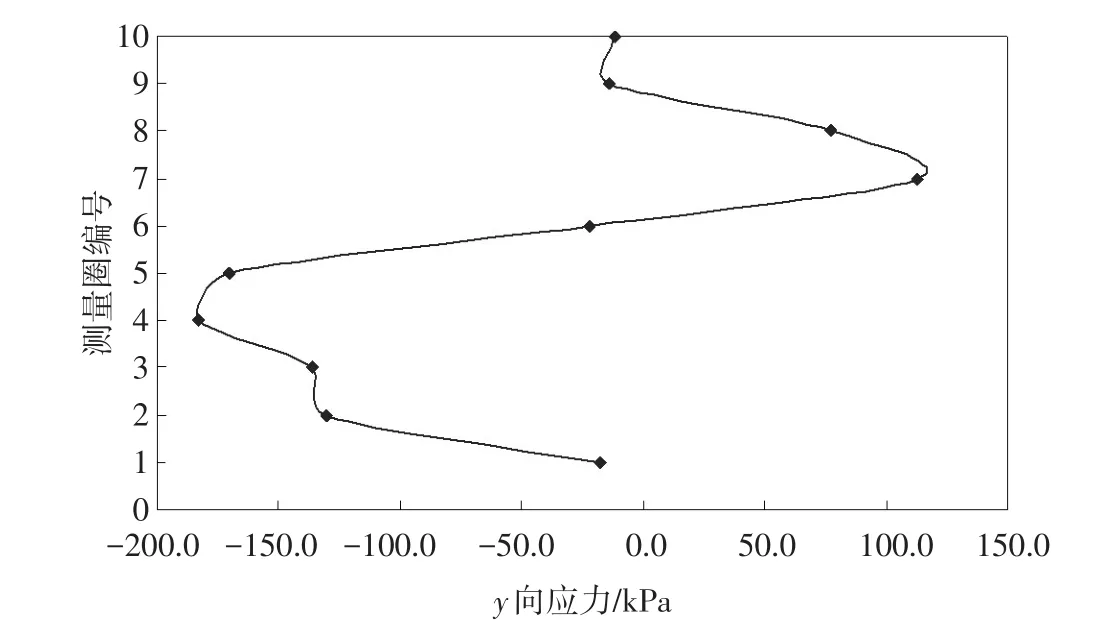
图7　锚杆轴向土体y向应力分布曲线

从图7可以看出，锚固段加载端附近（测量圈1-6）土体中应力为压应力，从加载端起，压应力迅速增大，峰值压应力位于测量圈4的位置，随后急剧减小至0，以测量圈6为界，形成拉-压应力交界面；锚固段末端附近（测量圈6-9）土体中的y向应力为拉应力，峰值拉应力位置接近锚固体底部与土体接触面（测量圈7）；当有多根锚杆共同作用时，锚固段末端的拉应力区相互叠加，容易造成锚根附近土体发生受拉破坏。

锚固体周围土颗粒中测量圈监测得出的剪应力分布曲线如图8、图9所示。由图8可以看出，从加载端到自由端（测量圈1到7），土体剪应力呈先增大后减小的趋势，当拉拔荷载超过极限荷载时，峰值点向自由端移动并持续增大。土体剪应力变化规律与室内模型试验中计算得出的界面黏结力相同，峰值点的位置及大小也近似，但数值并不相同，其原因是在模型试验中，应变片测试结果为一点应变，计算得出的界面黏结力为一点应力，而数值模型中测量圈获得是所包含土颗粒的平均剪应力，因此土体剪应力和界面黏结力结果有偏差。由于真实的破坏面并非平面，且产生在土体一侧，因此土体平均剪应力分布有一定的参考价值。由图9可以看出，在拉拔荷载作用下，锚固体附近土体剪应力较大，随着和锚固体距离的增大，剪应力大致呈负指数规律衰减。

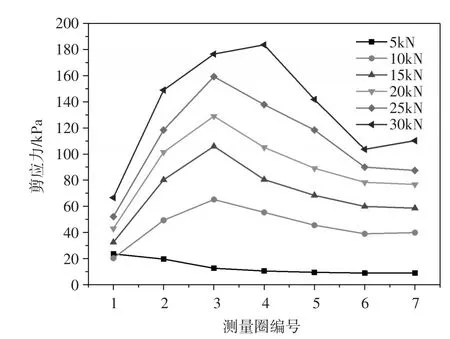
图8　各级荷载下土体剪应力轴向分布　

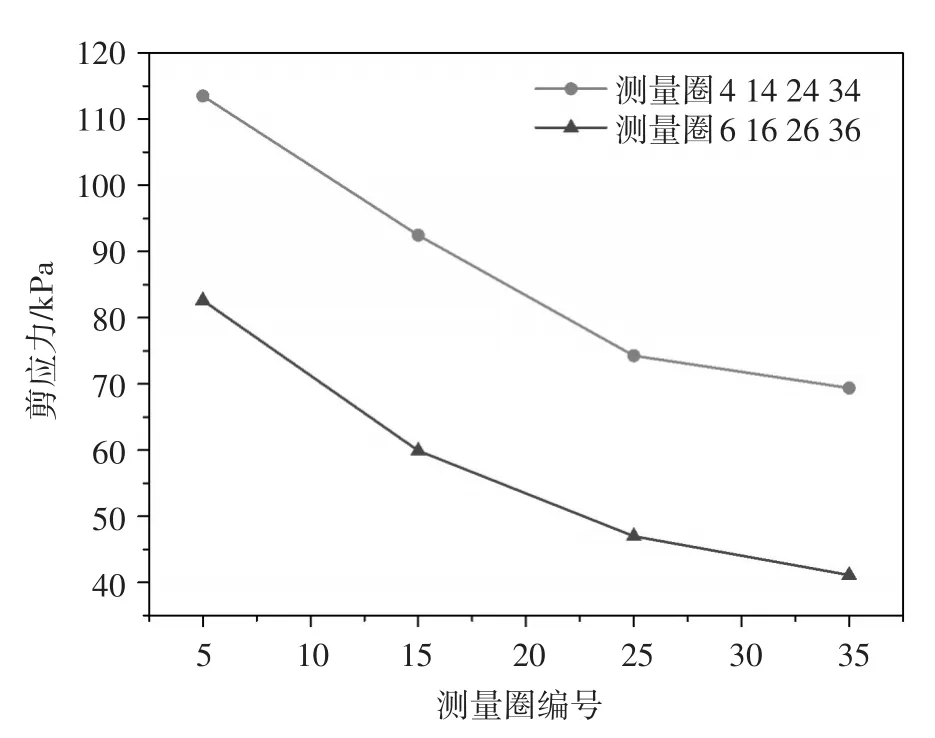
图9　拉拔荷载20kN下土体剪应力径向分布

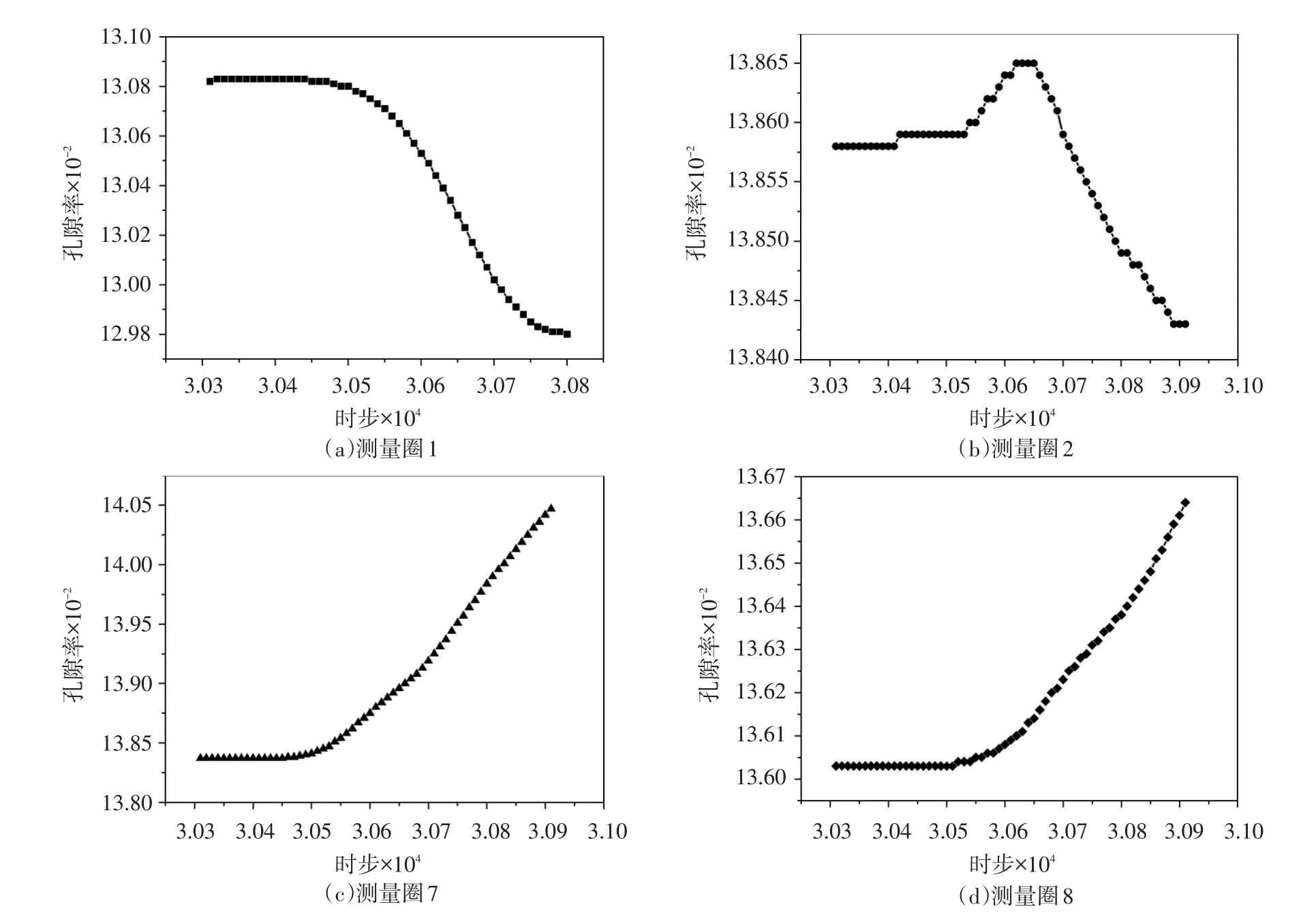
图10　土体孔隙率随时步变化

3.3.2土体孔隙率变化土体在拉力或剪力的作用下，颗粒将转动或产生反向位移，导致接触面积减小，孔隙率增大；当土体受压应力作用时，颗粒则相向移动，接触面积增大，孔隙率降低。因此，土体颗粒孔隙率变化与应力变化有直接联系［16］。由测量圈获得的锚固体周围土体颗粒孔隙率的变化情况如图10所示，其中测量圈1和2位于加载端附近，测量圈7和8位于则接近自由端。由图10可以看出，在加载端（测量圈1和2），由于土体受压力作用，因此孔隙率随时步降低；而在自由端（测量圈7和8），土体受拉力作用，孔隙率随时步逐渐增大。对于锚固段拉、压力交界面附近土体，由于拉压应力状态与荷载等级及平衡状态有关，孔隙率也会有增大和减小的波动状态。

4　结论

通过中心拉拔的大比尺模型试验，测试了高聚物锚固体与土体黏结特性，同时从细观力学角度出发，采用颗粒流软件（PFC2d），建立了“锚杆杆体-高聚物锚固体-土体”的三介质数值模型，对高聚物锚固体系进行了仿真模拟，探讨了土体颗粒的响应过程，结论如下：（1）土层中高聚物锚固体加载端位移与拉拔荷载近似呈指数关系，锚杆残余强度与峰值强度相当，无界面软化现象；接触界面黏结应力非均匀分布，沿锚固深度先增后减，由于高聚物材料弹性模量较小，因此相较于水泥砂浆锚固体，锚杆轴力和界面黏结应力集中程度较小。（2）锚固段区域内分别存在压应力和拉应力集中区：加载端附近土体受压，孔隙率有降低趋势；自由端附近土体受拉，孔隙率有所增大；拉压应力区的交界面随荷载水平变化有所变化，拉、压应力区交界面附近土体的孔隙率随压力变化有所波动。（3）荷载较低时，土体剪应力沿锚固深度减小；随着拉拔荷载的增大，土体剪应力先增大，后减小，最终趋于稳定；距离锚固体越远，土体剪应力越小，并呈现负指数降低的规律。（4）在锚杆相关试验中，锚固界面黏结应力测试一般采用间接计算获得，而锚固体周围土体随拉拔荷载作用的变化则更为复杂，影响因素更多，测试元件不易布置。借助颗粒流模拟模型研究锚杆界面应力径向传递和土体动态变化，是一种先进可行的手段。