基于L-M算法的微地震定位方法

徐克彬 陈祖斌 刘玉海* 任勇强 白田增 冉令刚

(①中国石油渤海钻探井下作业公司，河北任丘 062552；②吉林大学国家地球物理探测仪器工程技术研究中心，吉林长春 130061)

1 引言

水力压裂技术是开发低渗油气藏有效手段，微地震监测则是水力压裂技术的关键环节[1-3]。该技术通过注水压裂的方式，造成周围岩层破裂，从而激发一系列可观测的微弱地震信号[4]。随着水力压裂技术不断进步以及油田勘探开发要求不断提高，微地震实时监测已成为一种必然的趋势[5-9]。因此在保证定位可靠性的前提下，研究一种计算速度快的微地震定位算法非常必要。

传统的微地震定位算法主要以经典Geiger定位方法及其改进算法为主。宋维琪等[10，11]在Geiger定位方法基础上，通过扰动速度模型找到最佳微地震事件的等效速度，进而对微地震事件进行定位；毛庆辉等[12]采取将常规的极化分析约束与空间约束相结合的思路，将空间约束项加入旅行时残差目标函数，对常规反演结果进行重定位；李会义等[13]采用牛顿迭代法对Geiger方法中微地震定位方程组进行求解。以上方法往往需要从地震记录中拾取准确的纵横波旅行时信息，通过求解方程组获取震源位置。其主要特点是计算速度快，但由于必须要将地下视为一个匀速等效体，并且在拾取有效信号时会受到数据信噪比的影响，微震事件定位可靠性较低。近年发展起来的振幅叠加网格搜索类定位方法能够有效解决上述问题，如吕昊[14]提出了逆时偏移振幅叠加微地震定位方案； Anikiev等[15]提出了沿绕射曲线叠加微地震信号相位和振幅； Zhebel等[16]提出基于波形互相关的振幅叠加定位方法； Jiang等[17]利用射孔波形振幅叠加方案，对微震监测工区地下速度模型进行校正； Liang等[18]提出一种震源位置及震源机制联合反演方法(JSSA)。该类方法无需拾取地震旅行时，而是将整个地震记录信息作为输入，能有效抑制噪声，增强有效信号强度，并且可引入较复杂的速度模型，大大提高了微震定位的可信度。但该算法由于无法求得震源位置的解析解，需要在地下目标区域内进行逐点搜索，当要求定位精度较高时，计算效率较低，无法适应压裂监测的实时要求。为此，本文采用Levenberg-Marquardt(L-M)反演算法对常规绕射偏移叠加类定位方法进行改进，根据地面埋置的三分量检波器，获取射线入射方位角，利用射线路径回推的方法寻找震源位置。在保证计算精度的情况下，大幅提高了计算效率。模型试算和实际数据实验验证了改进后算法的优势。

2 绕射偏移叠加类定位方法及其改进

2.1 绕射偏移叠加类定位方法

绕射偏移叠加类定位方法的主要思想是沿时间方向进行逐个样点扫描，首先利用STA/LTA方法识别微震信号，将识别出微震信号作为输入数据，利用较多数量单分量检波器对各道数据进行叠加，该方法更适用于处理信噪比较低的地面监测方案，具体实施方案如下。

首先选取一道具有相对较清晰的初至同相轴作为参考道，将有可能发生微震事件的三维目标区域按照一定的边长划分出一定数量的三维网格，并把每个网格中心点视为一个潜在可能的震源位置。通过射孔炮校正初始速度模型[19-21]，利用射线追踪技术得到各道相对参考道的计算旅行时差

Δtcal=[Δt1，Δt2，…，ΔtL]

=[t1-tc，t2-tc，…，tL-tc]

(1)

式中：tc为震源点到参考道旅行时；tl为各道旅行时；L为检波器个数。每道地震记录按相对于参考道的计算旅行时差Δtcal进行偏移后叠加，可获得地下第i个网格中心点(xi，yi，zi)的能量总和

(2)

式中：S(xi，yi，zi，l，j)为在所选取的第i个网格中心到第l个检波器、j时刻的振幅；N为时窗长度。如果该网格为微地震事件发生处，那么经多道叠加后，整体信号会放大若干倍，大幅提高信噪比，反之，整体信号不会获得加强，甚至会相互抵消，如图1所示。

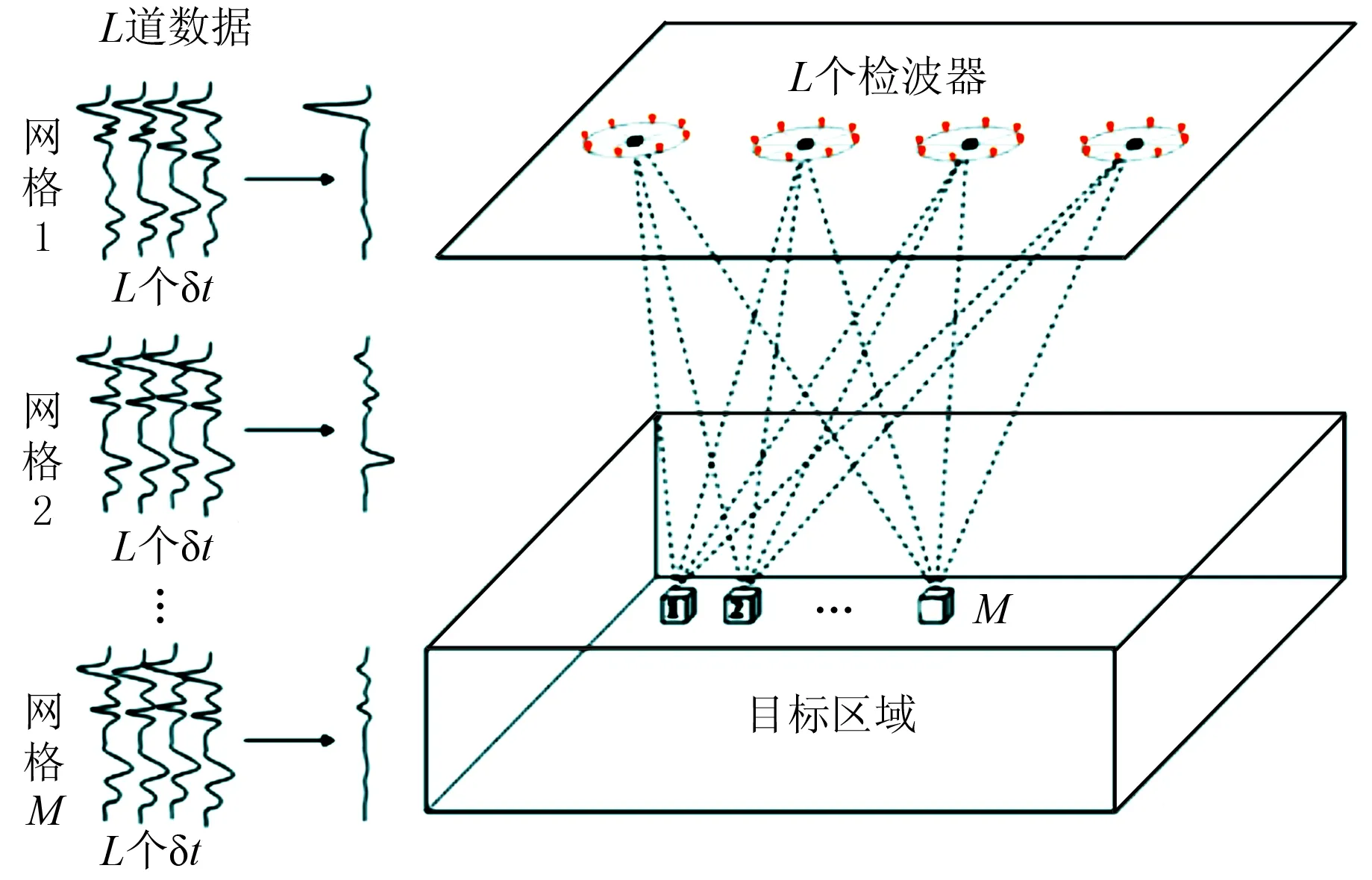
图1 偏移绕射叠加类微地震定位示意图

2.2 微地震事件定位的L-M算法

L-M算法是针对Gauss-Newton算法[22，23]的一种修正算法，是用于求解非线性问题的经典方法。进行局部最优值搜索时，具有快速稳定的特点。L-M算法通过引入修正参数以克服Gauss-Newton算法对于雅克比矩阵必须满秩的要求[24-26]。对于第k次迭代，L-M算法基本表达式为

JT(mk)[F(mk)-d]

(3)

式中：m为模型参数向量；F(m)为正演算子；d为目标数据向量；λk为正实数；I为单位矩阵；J(m)为雅克比矩阵。

由射线理论可知，一维层状模型中任意两点之间的旅行时为

(4)

式中：K为射线穿过地层的层数；hj为射线穿过第j层的有效厚度；vj为第j层的速度；p为射线参数。

在利用L-M算法进行微地震定位时，可设目标区域某点到各检波器射线参数m=P=[p1，p2，…，pl，…，pL]为模型参数向量，l为第l条射线。d=Δtcal为目标数据向量。假设第一道为参考道，可导出雅克比矩阵表达式为

(5)

拾取监测区域三维坐标点到检波器的时间差，以此作为雅克比矩阵元素，将式(5)代入式(3)，不断迭代求得射线参数P，进而可求出各道检波器能量叠加值，并判断能量叠加值是否满足收敛条件，其中收敛条件为两次迭代能量差|Ek-Ek+1|<ξ，ξ为可接受的误差值。如果达到收敛条件，根据地面所布置的三分量检波器，获取地震初至波形水平分量及垂直分量，确定射线路径入射方位角，由入射方位角及射线参数P，可将射线路径逆时回推。由于速度模型与实际情况有误差等原因，射线难以聚焦于一点，因此需要对初始能量值聚焦最高点处进行网格细剖分，并统计网格射线密度，射线密度最高的网格中心点，即视为微地震震源发生位置。然而由于L-M算法属于局部最优算法，在实际定位过程中，需要对震源点进行全局搜索，为保证计算效率，本文提出一种先进行网格粗剖分，寻找能量聚焦较高的区域，再利用L-M算法进行局部能量最高值搜索，其具体实现流程如图2所示。

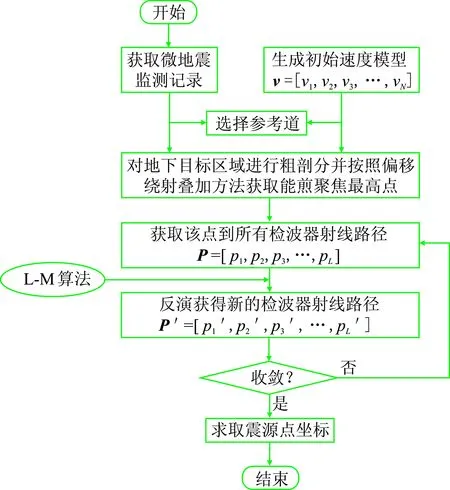
图2 本文改进算法流程

3 数据实验

3.1 模型数据试验

通过合成数据试验对比改进前算法与采用改进L-M算法的计算精度和效率，该合成试验是在“Intel-core i7-CPU @2.80GHz内存20GB”的平台上完成。速度模型如图3所示，地震正演波形采用50Hz的雷克子波进行描述，模拟震源位置坐标为(225m，-147m，962m)。微地震地面检波器呈星形排列，共96个。目标区域设定为x∈[-200m，200m]，y∈[-200m，200m]，z∈[1000m，800m]，采用改进前算法微地震定位时网格尺寸剖分如表1所示。改进后的算法首次粗剖分网格尺寸为40m。试验采用对正演结果加入信噪比为0.3的噪声数据(图4)。

从表1可以看出，随着网格尺寸逐渐减小，改进前算法定位精度逐渐提高，但同时增加了大量计算时间，无法满足微地震定位实时性的需求，而经过本文引入L-M算法后，仅用时17s，就可以使定位精度提高至2m以内，大大增强了算法的实时性。图5分析了改进后算法网格首次粗剖分尺寸对计算精度与计算效率的影响，可以看出，当首次网格剖分尺寸为50m时，出现了定位异常，这是由于网格首次粗剖分尺寸过大会导致首次网格搜索时，中心点无法落入能量聚焦包络区域所致。但是在实际微震监测工程中，由于地层吸收的原因，大部分高频信号被吸收[15]，因此，本文方法适用于绝大多数微地震事件定位。

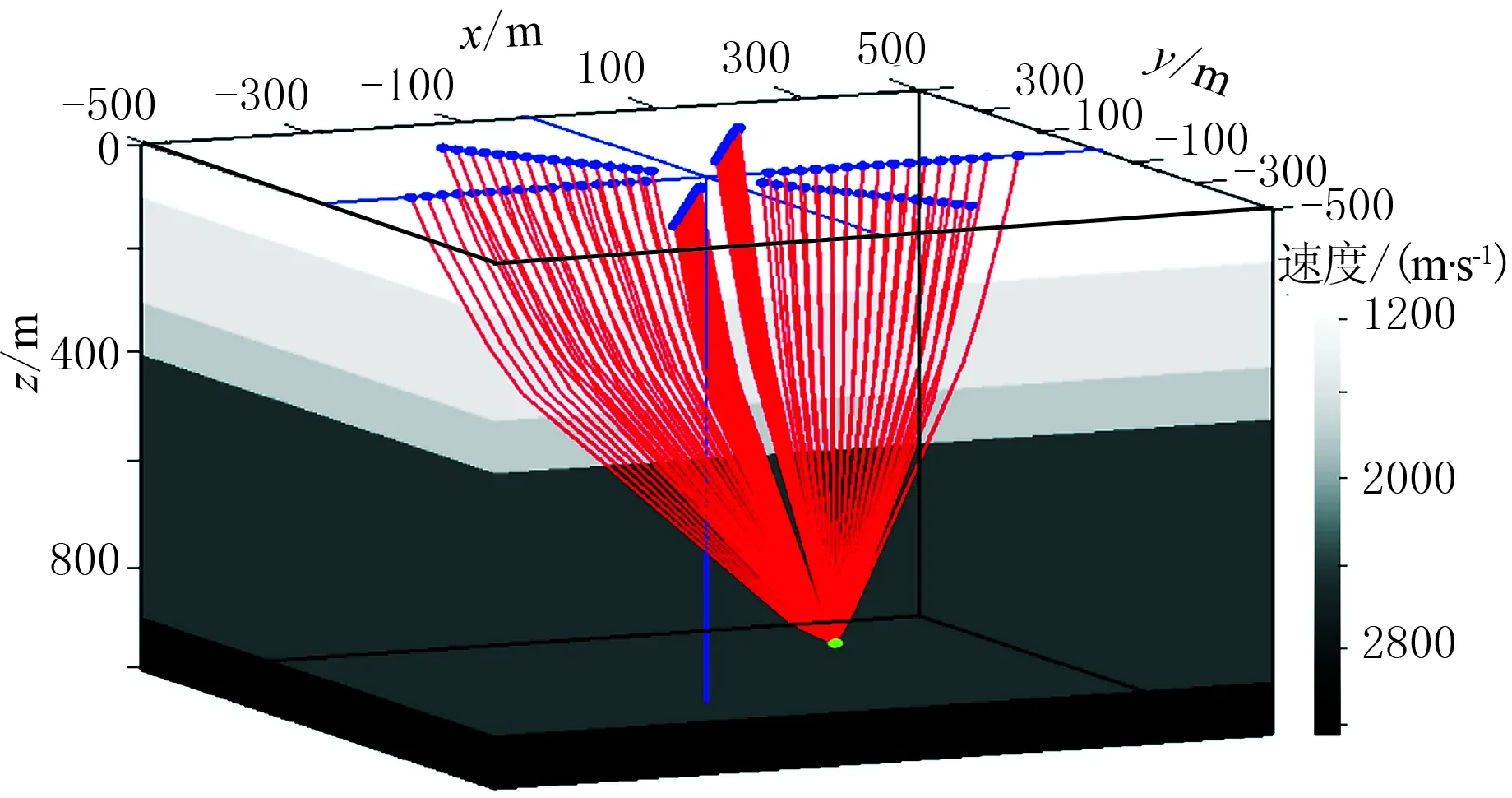
图3 检波器布设及速度模型示意图

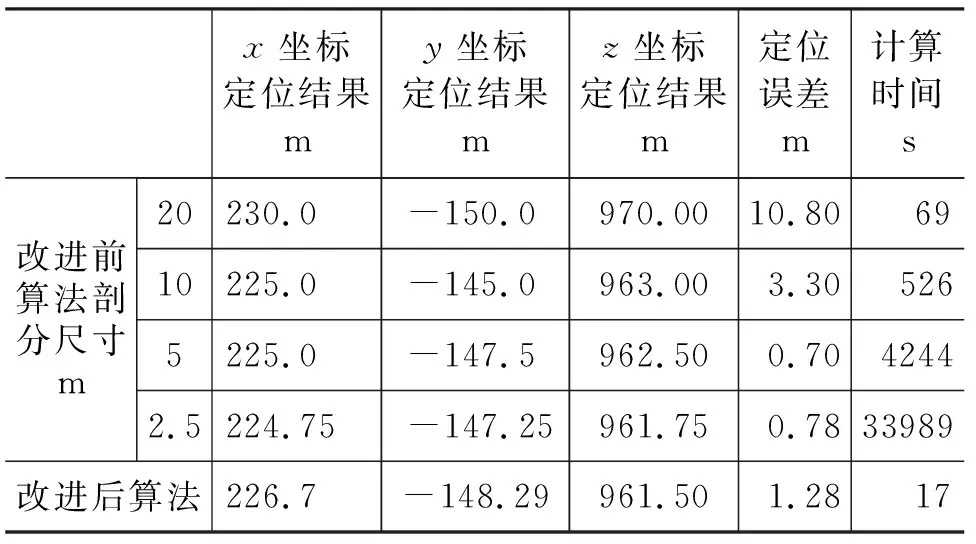
x坐标定位结果my坐标定位结果mz坐标定位结果m定位误差m计算时间s改进前算法剖分尺寸m20230.0-150.0970.0010.80 6910225.0-145.0963.003.30 5265225.0-147.5962.500.7042442.5224.75-147.25961.750.7833989改进后算法226.7-148.29961.501.28 17

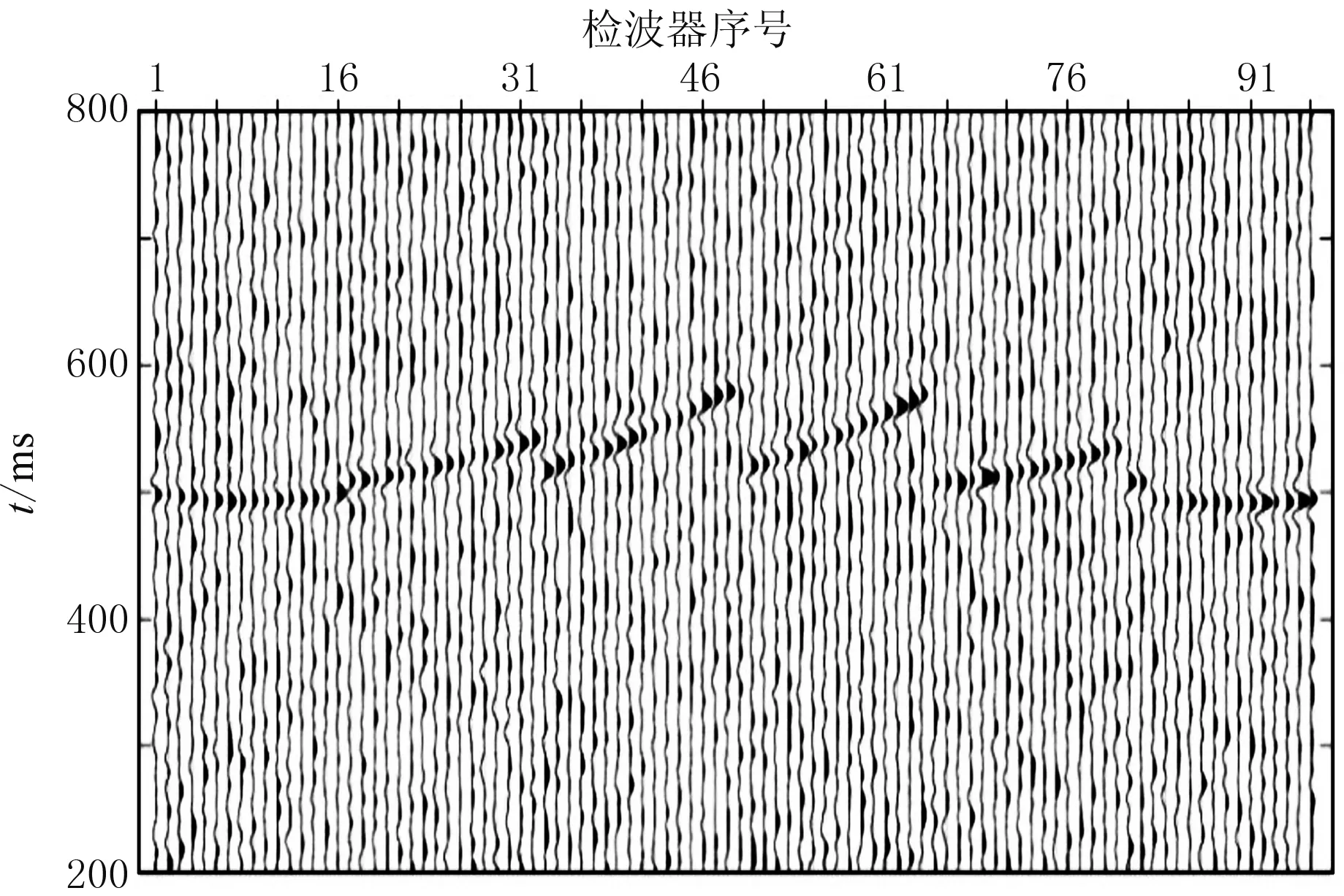
图4 信噪比为0.3时96道合成数据结果

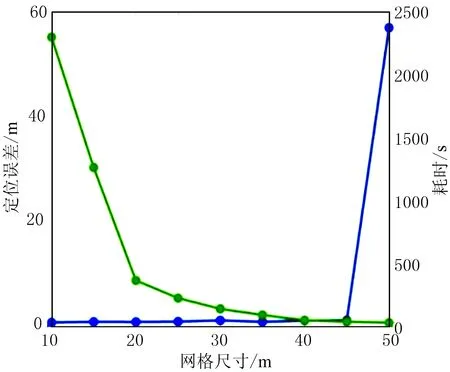
图5 改进算法定位精度和计算效率随网格首次粗剖分尺寸的变化曲线

3.2 实际资料处理

将本文方法应用于实际微地震资料分析与处理。根据当地实际地貌，本次监测布置了A～F共六条测线，每条测线布设6、7个三分量检波器，检波器间距为80m(图6)。以射孔点水平坐标作为中心坐标原点，射孔坐标为(0，0，1821m)。地下监测区域设为x∈[-300m，300m]，y∈[-300m，300m]，z∈[1771m，1871m]。图7为该资料中一个微地震信号垂向分量记录。图8a为改进前算法微地震定位结果，为保证现场数据处理的实时性，剖分网格尺寸为20m，计算时间约为2h； 图8b为改进后算法的定位结果，其初始网格剖分长度为40m，计算用时约为1h。从图8定位结果可以看出，改进前算法则出现“横平竖直”现象，对裂缝走向描述会存在一定误差； 改进后算法的定位结果更精细，更能准确反映实际裂缝走向，并可将计算效率提高一倍。

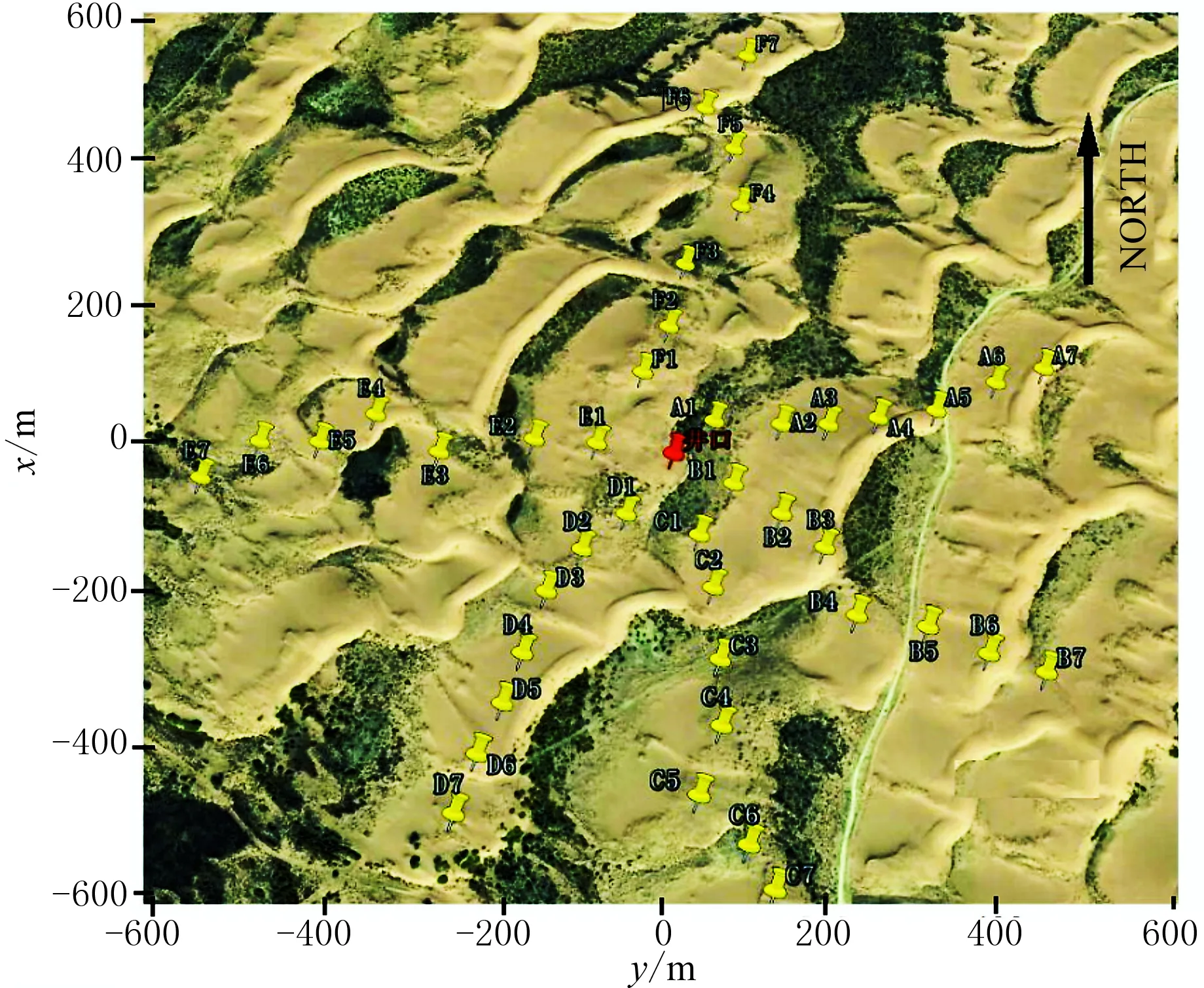
图6 野外试验地面检波器布设图

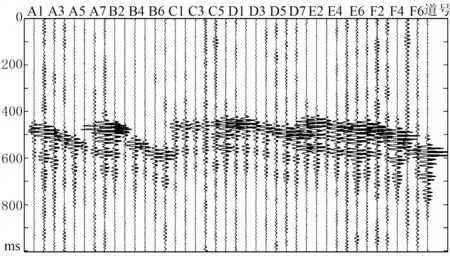
图7 微地震信号垂直分量

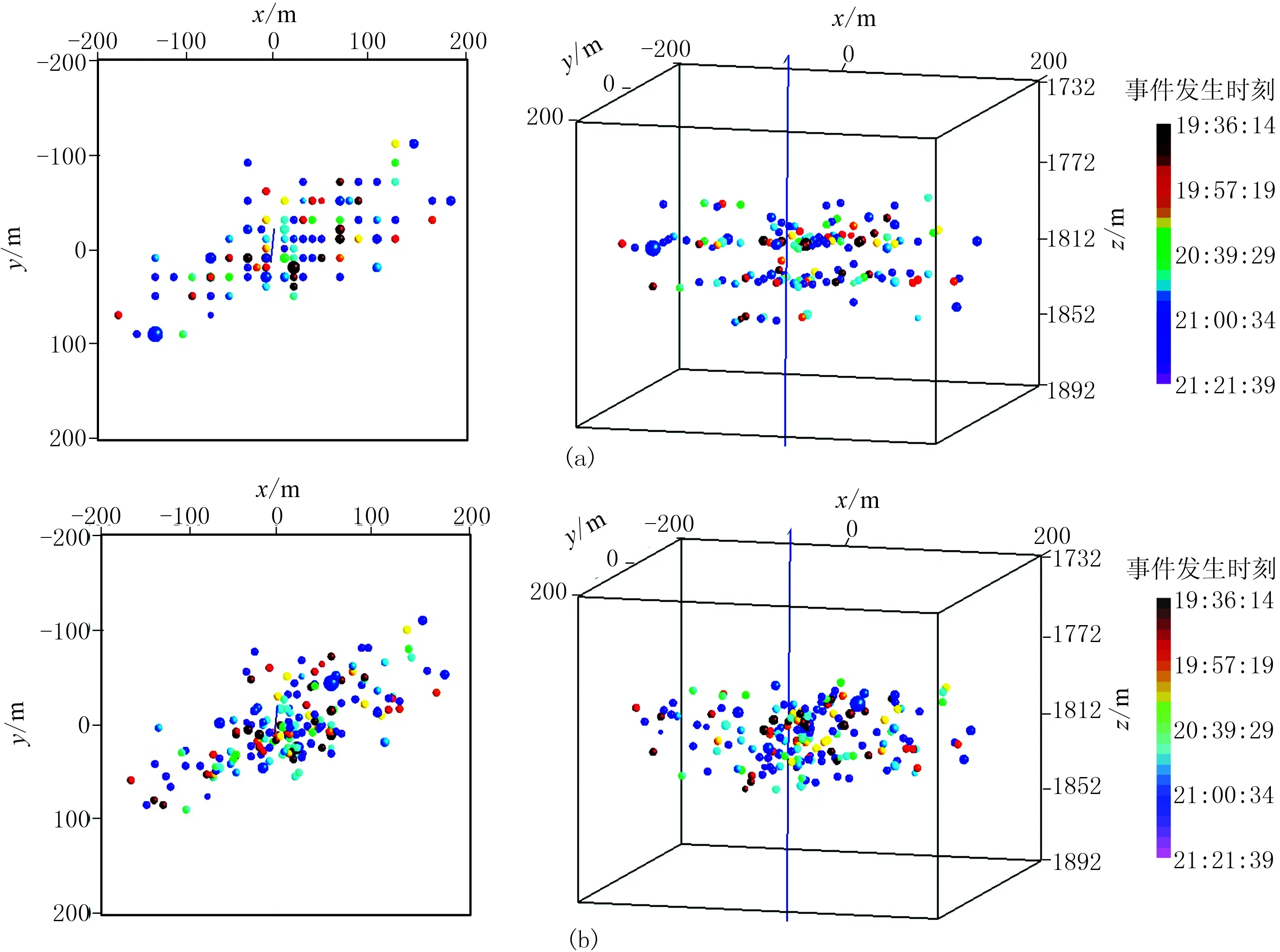
图8 改进前(a)、后(b)实际数据定位结果左：俯视图； 右：侧视图

4 结论与讨论

研究高效、精确的微地震定位技术在水力压裂工程中具有重要应用价值与现实意义。本文对传统基于网格搜索的振幅叠加微地震定位方法进行改进，实现了网格搜索法与L-M算法相结合的微地震定位技术。该算法在保证具有较高定位精度的同时，又具有快速、高效的特点，满足微地震定位的实时需要。模型试算与野外数据处理验证了方法的有效性。

微地震事件频率与首次网格剖分尺寸会对本文改进算法造成一定影响。当微震事件频率较高、网格首次剖分尺寸较大时，网格中心点不能落入能量聚焦较高区域，则会造成定位失常。但由于地层吸收以及微地震事件传播特性等原因，地面所获得的大多数信号为低频信号，因此本文算法可用于绝大多数微地震地面监测。在进行井下监测时，应根据实际地震波频率设计首次网格剖分尺寸，或采用传统方法与改进方法相结合的方式，以减少定位失常现象。