稀疏反射系数频率域正余弦分量协同反演方法

张繁昌 何晋越 桑凯恒* 秦广胜 张佳佳

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②中国石化中原油田分公司，河南濮阳 457099)

1 引言

随着油气资源勘探程度的不断加深，对勘探精度的要求也越来越高，即对地震资料的分辨率提出了越来越高的要求。由于受调谐效应的影响，应用常规地震资料及传统处理方法无法识别厚度小于调谐厚度的薄层和小尺度地质构造，难以提供高精度的解释成果。识别调谐厚度以下的信息，突破常规地震分辨率的极限是近年来地震领域资料处理研究的重点之一[1]。Portniaguine等[2，3]提出了谱反演方法，它不依赖测井资料等先验信息，只需利用地震数据本身的频谱信息就能反演地层稀疏反射系数； Chopra等[4，5]对谱反演方法进行了详细的论证、推导； Castagna等[6]提出奇偶分解理论； Puryear等[7]对奇偶分解理论进行详细阐述，把稀疏脉冲反射系数分解成奇、偶脉冲分量，进一步提高了谱反演对小于调谐厚度的薄层的分辨能力； Yuan等[8]给出了一种奇偶分解谱反演的等价矩阵形式； 刘万金等[9]、陈祖庆等[10]、张华等[11]及刘洁等[12]应用谱反演理论并结合不同反演算法对实际地震资料进行处理，均取得不错的效果。

在时间域对反射系数进行奇偶分解，需给定奇偶脉冲分量的时间厚度，该参数对反演结果的影响很大且不易确定。研究发现，在时间域将反射系数序列分解成奇、偶脉冲分量，与在频率域将反射系数序列的频谱分解成正、余弦分量是等价的。基于此等价关系，本文提出一种直接在频率域利用地震数据谱的正、余弦分量进行协同反演的方法，推导出反演目标函数。对反演目标函数的求解有多种方法[13-16]，为了获得稀疏反射系数序列，本文根据压缩感知理论，采用梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction，GPSR)基追踪算法[17，18]对目标函数进行求解。通过一维稀疏脉冲反射系数模型和实际地震资料反演，对频率域正、余弦分量协同反演结果与稀疏脉冲反演结果进行对比，证明频率域正、余弦分量协同反演方法能取得高分辨率反射系数序列，有助于识别原始地震剖面上无法分辨的薄层，且反演剖面的信噪比得到提高。

2 方法原理

2.1 正、余弦分量协同反演基本原理

正弦和余弦信号的傅里叶变换为

F[sin(ω0t)]=jπ[δ(ω+ω0)-δ(ω-ω0)]

(1)

F[cos(ω0t)]=π[δ(ω+ω0)+δ(ω-ω0)]

(2)

由傅里叶变换的对称性质，即已知F(ω)=F[f(t)]，则F[F(t)]=2πf(-ω)，可得到

F[δ(t+t0)-δ(t-t0)]=2jsin(t0ω)

(3)

F[δ(t+t0)+δ(t-t0)]=2cos(t0ω)

(4)

其对应波形及频谱如图1所示。

由此可知，时间间隔为2t0的奇脉冲分量在频率域表现为以t0为周期的正弦分量，时间间隔为2t0的偶脉冲分量在频率域表现为以t0为周期的余弦分量。根据Puryear的奇偶分解理论，假设反射系数是稀疏脉冲的，任意反射系数序列都可以分解成奇、偶脉冲分量，因此，对应于频率域，任意反射系数的频谱可以分解成正、余弦分量。 因此将反射系数频谱分解成正、余弦分量，构建用正、余弦分量表示的目标函数，在频率域进行正、余弦分量协同反演。

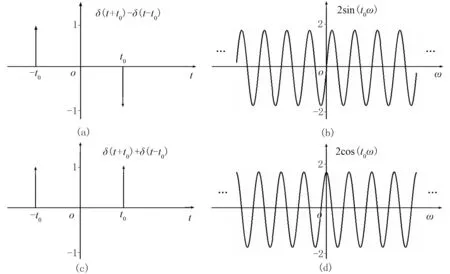
图1 奇脉冲分量(a)、偶脉冲分量(c)及其对应频谱(b，d)

反射系数序列r(t)可表示为

(5)

式中：rn和tn分别为第n个采样点上的反射系数值和对应的时间位置；N为采样点个数。

根据褶积模型[19]，地震信号s(t)可表示为

(6)

式中：w(t)为地震子波； “*”表示褶积运算。对式(6)做傅里叶变换，即得褶积模型在频率域表达式

(7)

式中：f为频率；S(f)、W(f)和R(f)分别为地震信号s(t)、地震子波w(t)和反射系数序列r(t)的频谱。因此反射系数序列r(t)的频谱可表示为

(8)

对式(8)分别取实部和虚部得到

(9)

(10)

式中aWmax为白噪因子，可防止分母出现零值。其中：Wmax为地震子波频谱W(f)的最大振幅值；a是一个很小的系数(一般取0.01)。将式(4)、式(3)分别代入式(9)、式(10)，得到

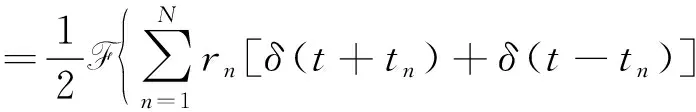
(11)

(12)

由此可见，反射系数频谱实部是不同系数、不同频率的余弦分量的叠加，这里的系数就是各采样点的反射系数值rn，频率即为该反射系数值对应的时间位置tn，同时，这一系列余弦分量对应于时间域一系列偶脉冲分量。同理，反射系数频谱虚部是正弦分量的叠加，在时间域对应于一系列奇脉冲分量。

地震信号频带宽度都是有限的，即地震信号都是带限信号。以M区一道地震记录为例，其振幅谱如图2所示，可知其只在5～85Hz范围内有明显的振幅值(红框内部分)。设选取的地震信号频率范围是[fmin，fmax]，频率采样间隔为Δf，有

fm=(m-1)×Δf+f1m=1,2,…,M

(13)

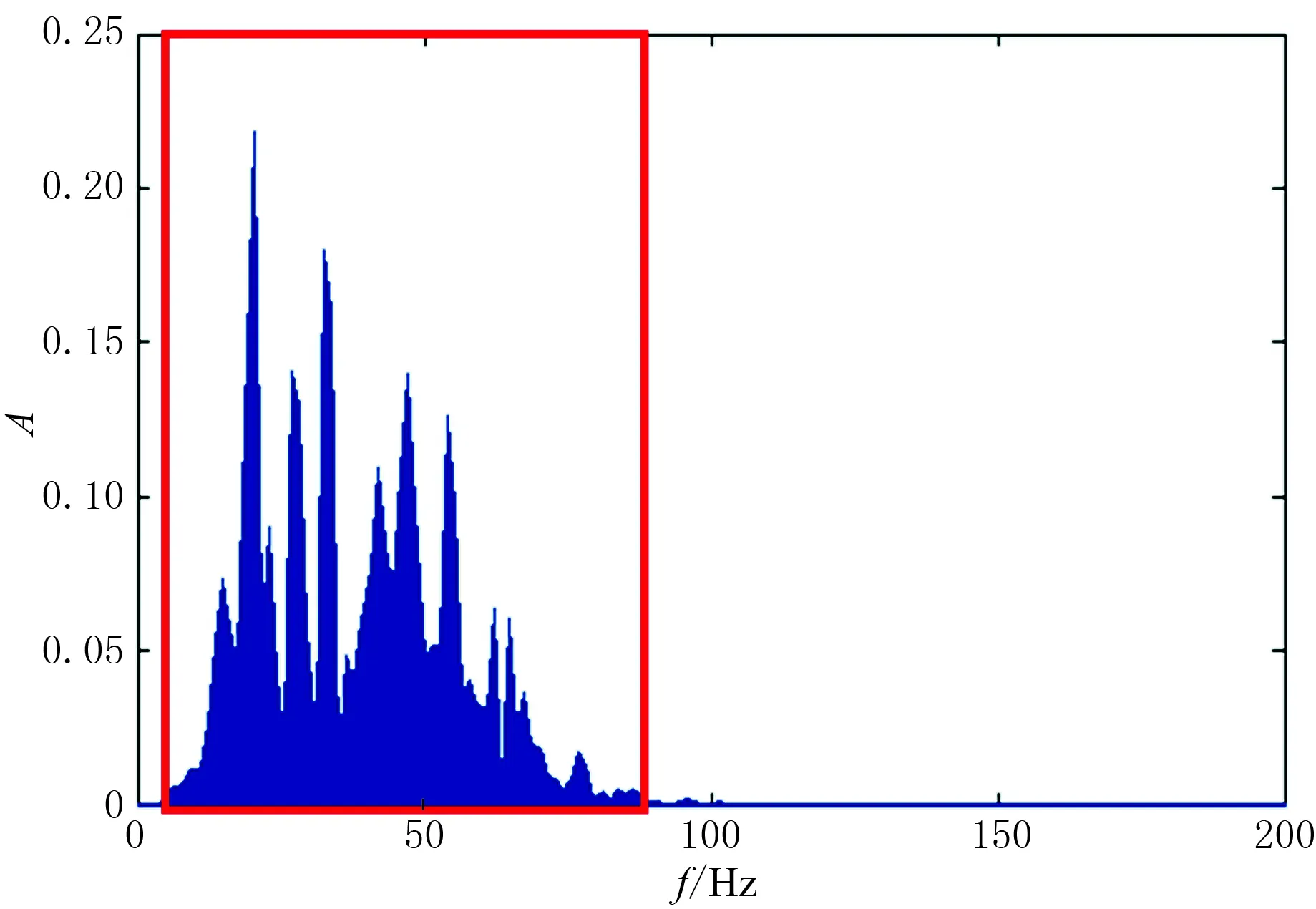
图2 M区一道地震记录的振幅谱

在[fmin，fmax]内对式(9)、式(10)进行离散，建立反射系数离散谱方程

(14)

将式(14)改写成矩阵形式

(15)

其中

Cmn=cos(2πtnfm)

Smn=sin(2πtnfm)

r=[r1,r2,…,rn]T

式中：C即余弦分量矩阵；S即正弦分量矩阵；r为反射系数序列组成的向量。式(15)即正、余弦分量协同反演目标函数表达式。

2.2 GPSR算法

为了求解稀疏的反射系数序列，应使用稀疏约束的基追踪算法对目标函数进行求解。目前有大量文献提供了各种基追踪求解算法[20]，本文选用梯度投影稀疏重构(GPSR)算法对式(15)进行求解。

将目标函数式(式(15))改写为基追踪的标准形式

(16)

将待反演的反射系数序列r分解为正数序列u和负数序列-v，则r可写成r=u-v(u≥0,v>0)，因此r的L1范数可写成

(17)

式中ln=[1,1,…,1]1×n。将式(17)代入式(16)，则求解式(16)转为求解目标函数

(18)

进一步进行下列变换

(19)

即得到新的目标函数表达形式

(20)

通过以下步骤的迭代，最终求得式(20)的解。

(1)初始化， 给定z(0)，λ=0.01， 选择参数β∈(0,1)，μ∈(0,0.5)，令k=0；

(2)利用式(21)和式(22)计算α0， 并用mid(αmin,α0,αmax) 代替α0；

(21)

(22)

(23)

(4)进行收敛判定，并在结果满足精度要求时终止迭代;如果不满足精度要求，则令k=k+1，返回步骤(2)。

3 模型和实际数据测试

3.1 理论模型试验

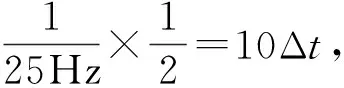
为了体现正余弦分量协同反演的优势，将时域褶积模型直接作为目标函数，并采用业内常用的稀疏脉冲反演方法[24，25]进行反演，将其结果作为对比。稀疏脉冲反演目标函数为

(24)

式中：W为子波矩阵；s为观测得到的地震信号组成的向量。

本模型的稀疏脉冲反演结果如图3e所示，它与25Hz的Ricker子波合成的地震记录如图3f所示。观察图3d和图3f可发现，两种方法得到的反射系数恢复出的合成地震记录与模型正演地震记录匹配较好，但对比图3c与图3e可看到，基于GPSR的正余弦分量协同反演结果与模型匹配得很好， 反射系数的位置、幅值都能较为精确地匹配，而稀疏脉冲反演结果中，大部分反射系数值恢复不到位，第2、6组不能将两个脉冲信号完全分开，而第4、8组反演结果时间间隔偏大，且在相反极性对两侧出现模型不存在的脉冲。试验说明，基于GPSR的正余弦分量协同反演能够识别时间间隔小于分辨率极限的反射界面，且反演结果稳定而精准。

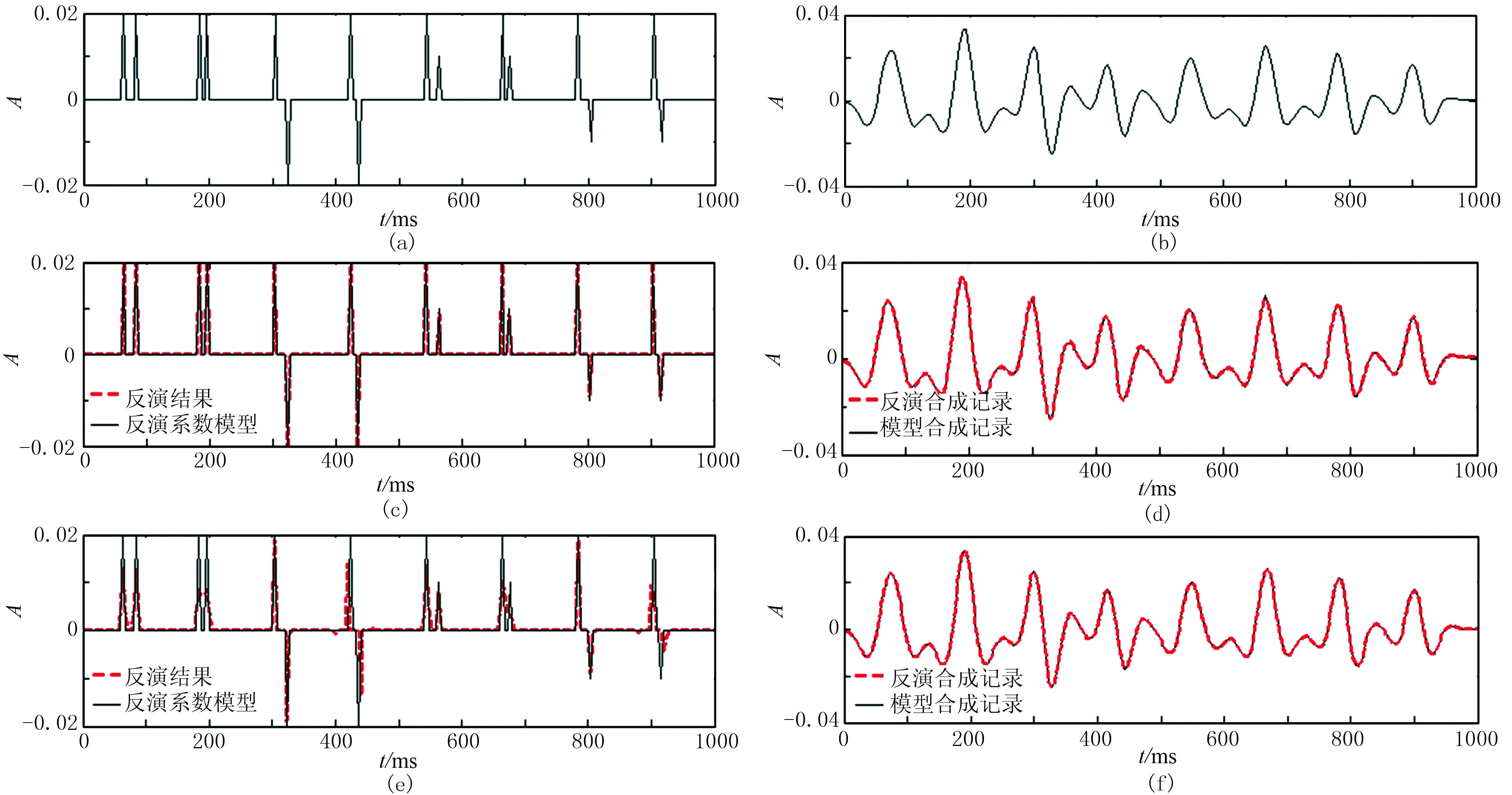
图3 一维理论模型试验结果

3.2 实际资料应用

为了进一步分析正余弦分量协同反演的实际应用效果，将其应用于中国东部E区一过井测线的实际地震资料(图4a)。基于GPSR的正余弦分量协同反演过程中采用的地震子波由谱模拟法[26]估计得到，同时根据地震频谱选取5～70Hz为地震有效频带，反演获得的反射系数剖面如图4b所示。作为对比，稀疏脉冲反演获得的反射系数剖面如图4c所示。 对比图4a与图4b可见，相比原始地震剖面基于GPSR的正余弦分量协同反演获得的反射系数剖面明显具有更高的分辨率，能将由于相干形成的复波同相轴分离开来，识别原始地震剖面上无法分辨的、厚度小于调谐厚度的薄层和小尺度地质体，反映地层真实的接触关系，刻画地层真实的尖灭位置，提供高分辨率的、更加丰富的地质信息。对比图4b与图4c可见，基于GPSR的正余弦分量协同反演结果相较于稀疏脉冲反演结果在保持良好信噪比的同时分辨率有明显提升，能识别出更小厚度的薄层，且横向连续性更好，有助于薄互层、小尺度地质体的精细识别。观察三张图黑色虚线框内的部分，图4b的基于GPSR的正余弦分量协同反演结果能精细刻画小尺度地质体和薄层以及它们之间的接触关系，而在图4c的稀疏脉冲反演结果中薄层反射轴无法分开，有效信息被淹没，不能反映地质构造的真实样式。

图4 实际资料应用结果

4 结束语

研究发现，时间域的奇偶脉冲分量与频率域的正余弦分量是彼此等价的。在时间域对反射系数进行奇偶分解，需要给定奇偶脉冲分量的时间厚度，该参数对反演结果影响很大而且不易确定。而以此等价关系为基础，直接在频率域利用地震数据谱的正余弦分量进行协同反演可避免此问题。从反演算法看出，本文反演方法不依赖于测井资料等先验信息，只需要地震数据本身的频谱信息就能反演得到地层稀疏反射系数。

从模型测试和实际数据应用结果看，相比于时域褶积模型反演结果，正余弦分量协同反演在保持良好信噪比的同时，分辨率明显提升，能够识别原始地震剖面上分辨不出的、小于调谐厚度的薄层和小尺度地质体，更有利于地震沉积学研究。