检波器评估系统——一致性函数,相关运算以及传递函数分析

俞度立,Bernard MAECHLER,王之洋

(1.北京化工大学信息科学与技术学院,北京100029;2.ION Geophysical Corporation,Houston 77042)

近年来,采取何种方法比较地震勘探以及监测中的常规检波器和加速度计检波器的性能越来越成为国内外学者关注的焦点和研究的热点[1-4]。YU等[1]从理论上讨论了两种检波器的传递函数并在频率域比较了两种检波器的性能。HAUER等[2]用实验方法验证了YU等[1]给出的理论,他们设计了一种实验装置,使用扫描激光振动计(SLV)精确地测量两种检波器的输入信号,并分别记录它们的输出信号,结果发现,无论是普通检波器还是加速度计检波器,其输入、输出都与其理论模型一致。YU等[3]在时间域比较了两种检波器的性能,与YU等[1]在频率域的研究有相同的结果。KIMURA等[4]比较了不同类型的加速度计检波器的性能，发现针对相同的信号输入，不同类型的加速度计检波器之间记录的输出信号具有很高的相似性，这证明加速度计检波器具有很好的稳定性。

地震检波器是一种将地面振动转变为电信号的传感器,或者说地震检波器是将机械振动转化为电信号的机械装置。每个地震检波器都是由机械部分和与其相连的具有电负载的机电转换器组成,输出与速度成比例的称之为速度检波器,与加速度成比例的为加速度计检波器,与位移成比例的为位移检波器。理论上来说,当输入相同时,这3种检波器的输出不会存在差异,但是对这3种检波器进行更深入的研究发现,其输出结果不同。主要原因就取决于输入信号的特征,比如信号对应的带宽和干扰噪声的类型;另外,还在于检波器的制造公差以及环境参数(温度,湿度)的影响。当要比较这3种检波器的性能并判断哪一种类型的检波器性能更好时，通常存在以下3种情况：①这3种检波器测量的是位移、速度和加速度3种不同的物理量，无法以同一个标准比较它们的性能;②如果不存在噪声，这3种检波器测量的物理量就存在着完美微分转化关系;③反褶积可以解决检波器传递函数不完美的问题。

在数学上,可以使用多种方法来评估检波器的性能,其中较常用的方法是传递函数法。传递函数法基于检波器的频响特性曲线评估检波器的性能。传递函数是一个复值函数,同时考虑了检波器的幅频曲线和相频曲线。其中,针对不同检波器相频曲线的研究表明,不同检波器性能上最大的差异体现在对应的非线性相频响应的差异上。

我们研究的目的是揭示常规检波器和加速度计检波器固有的性能特性,描述两种检波器的性能差异以及这些性能差异对信号/成像质量的影响。建立一个统一的检波器性能评估体系,适用于所有种类的检波器,并可与理想检波器的性能作比较。

在前人[1-3]详细的理论推导的基础上,分析、总结了相关运算以及传递函数分析两种用于检波器性能评估的方法原理及优缺点,提出一种基于一致性函数的检波器性能评估方法,对不同类型的检波器的性能进行综合评估。一致性函数可以统一分析可能影响检波器性能的因素,比如制造公差、环境参数(温度、湿度)影响等,将振幅失真、相位失真、后处理调制以及影响信噪比的噪声等多个待分析变量统一为一个确定的量化值,即一致性函数值(取值范围为0到1),直观、简明、全面地评估检波器的性能。

1 早期的两种检波器性能评估方法

1.1 传递函数分析法

首先介绍传递函数分析法对不同检波器的性能进行评估的方法原理。

显而易见,如果一个检波器的传递函数近似于理想检波器的传递函数,那么这个检波器的性能就非常优秀。在时间域,理想检波器的传递函数具有零延迟或者有一个固定时延的特性,同时尺度因子为常数A0。相应地,在频率域,理想检波器的传递函数具有如下特性:在幅频响应中,其幅度在目标频段ωc里是常数;在相频响应中,其相位φ(ω)的变化是线性的。

式中:X(t),Y(t)分别代表输入信号和输出信号;τ0为时间延迟;ω为频率;H(ω)为频率域的检波器传递函数;φ(ω)为传递函数相频响应中的相位函数。

以油气地震勘探中的信号采集为例,阐述传递函数分析法对检波器性能进行评估的方法原理。

油气勘探的地震信号带宽范围通常是1～200Hz,在这个带宽范围内,加速度计检波器的开环传递函数是理想检波器传递函数的高度近似,因此,加速度计检波器有较好的性能。

图1为加速度计检波器和常规检波器的传递函数曲线。在油气勘探的地震信号带宽内,加速度计检波器的传递函数的振幅和相位响应都是非常平的,而常规检波器的振幅和相位响应却有两个零点与两个极点,与理想检波器的传递函数存在差异。另外,在低频段,常规检波器的相频响应曲线存在着一个-40dB/10Hz 的衰减,这将极大地降低检波器对信号低频成分的动态范围,暗示着信号能量的损失。从图1 的常规检波器的传递函数的频响特征曲线可知,频带过窄,需要对常规检波器进行反褶积处理以拓宽频带。理想的状况是:反褶积之后,时间域的传递函数是冲激函数δ(t)。

图1 传递函数曲线

因为检波器的传递函数是已知的,因此确定性反褶积算子可以应用于检波器的传递函数。由于噪声对信号的干扰以及反演算子的稳定性问题,确定性算子比统计算子的效果更好。我们在检波器上应用反褶积算子来说明反褶积算子的局限性、展示常规检波器和加速度计检波器的性能差异。

案例:阻尼系数有百分比值偏差的影响。

由于制造公差(对应每个检波器的阻尼系数有±2.5%的误差)以及环境因素(温度、湿度、整个检波器组的温差变化,线路内电阻和材料疲劳等)的不同,检波器实际的阻尼系数与标称的阻尼系数不同。那么,检波器阻尼系数的偏差对检波器性能造成什么影响呢？假设检波器的实际阻尼系数相较于标称阻尼系数有个百分比值的偏差,观察这个百分比值的偏差对检波器性能的影响。我们对检波器应用反褶积算子,得到其反褶积之后的传递函数,记为HS2。

设计两个不同的检波器以讨论检波器阻尼系数的偏差对检波器性能造成的影响,首先设计一个加速度计检波器,典型的设计参数为:谐振频率f=1000Hz,角频率ωn=2π·1000,阻尼系数为ζ=0.025。当加速度计检波器的阻尼系数有1%的偏差时,可以发现加速度计检波器的幅频响应中,幅值的最大不同出现在200Hz处,只有10-6数量级的偏差。在其相频响应中,相位的最大差异出现在1000Hz处,有小于0.285°的偏差。

其次,设计一个常规检波器,其典型的设计参数为谐振频率f=10Hz,角频率ωn=2π·10,阻尼系数ζ=0.7。当常规检波器的阻尼系数有1%的偏差时,可以发现在常规检波器的幅频响应中,其幅值在频段范围1～100Hz内都有偏差,如图2所示,同时,在其相频响应中,在频段范围1～100Hz内,其相位有±0.285°的偏差。

不同检波器最大的不同来自于非线性相频响应的差异,因此研究相位的差异可以反映检波器性能的差异,为了更直观地理解相位失真的概念,我们将群延迟和相延迟理论应用于检波器的传递函数HS2中。群延迟和相延迟分别为:

以常规检波器为例,图2给出了常规检波器在不同频段的群延迟和相延迟曲线。从图2可以看出,当常规检波器的阻尼系数有1%的偏差时,在0～200Hz的频段范围内,最大群延迟为±12ms。但在相同假设下,加速度计检波器的最大群延迟只有0.09μs(图中未显示)。

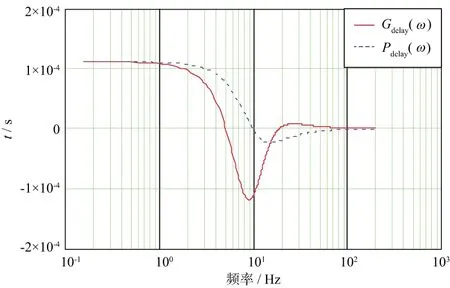
图2 常规检波器在不同频段的群延迟和相延迟曲线

1.2 最大时延相关法

最大时延相关法是一种统计学方法,相比于传递函数分析法,该方法可以处理噪声信号。同时,时间延迟也与信号源的空间位置一一对应,获取时延就可以通过计算得到信号源的空间位置。

假设时延为i,可以得到时延互相关函数为:

(5)

式中:x,y分别为输入信号和输出信号。

如果要研究两个信号之间的时间延迟,互相关函数是一个非常有用工具。基于公式(5),假设有两个信号,分别记为x和y(x和检波器脉冲响应褶积就得到y,即y是检波器接收信号x的输出结果),当时间延迟量i=0时,两个信号之间没有时延,记两个信号的互相关结果为Corr0。当时间延迟量i=1(即代表一个数字采样间隔Δt)时,记两个信号的互相关结果为Corr1。不断增加时间延迟量i的值,直到遍历信号所有采样点,获得两个信号的最大互相关值,此时i对应的与数字采样间隔Δt相乘的结果记为系统最大时延。系统最大时延反映的是检波器输入信号和输出信号的最大时间延迟程度,可以利用最大时延量评估检波器的性能。因此,设计以下8种不同参数以及不同种类的检波器,讨论如何利用系统最大时延来评估检波器的性能。

a)ζ=0.025,ωn=2π·1000;

b)ζ=0.025/2,ωn=2π·900;

c) 理想反褶积,没有参数漂移,预白系数α=0.1%;

d)ζ=0.7·(1-0.025),ωn=2π·10,预白系数α=0.1%;

e)ζ=0.7,ωn=2π·10·(1-0.025),预白系数α=0.1%;

f)ζ=0.7·(1-0.025),ωn=2π·10·(1-0.025),预白系数α=0.1%;

g)ζ=0.7·(1-0.025),ωn=2π·10·(1-0.025),高噪声,预白系数α=0.1%;

h)ζ=0.7·(1-0.025),ωn=2π·10·(1-0.025),预白系数α=1.0%。

检波器a和检波器b是加速度计检波器,检波器c到检波器h是常规检波器。其中,检波器a是典型的加速度计检波器,检波器b改变了检波器a的两个参数,作为对照组。对加速度计检波器进行测试后得到以下结论:在正常的加速度计检波器操作环境以及时间周期内,不同设计参数的加速度计检波器输出信号之间的时延差异远远小于加速度计检波器参数的改变,因此,加速度计检波器非常稳定,性能很好。常规检波器c是一个理想检波器。检波器d到检波器h分别考虑了检波器制造和操作环境等因素,设定了不同的参数,观察不同参数下检波器的系统最大时延,并评估检波器的性能。本文中信号的采样间隔Δt=25μs,延迟是一个基于所有数据的统计学概念,因此,有12.5μs的不确定性。

我们使用Ricker子波作为输入信号,加速度计检波器和常规检波器的输出结果如图3所示。由图3 可以观察到不同检波器的系统时延。

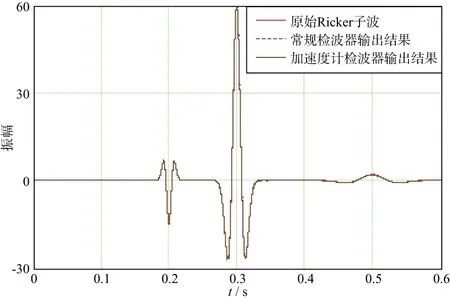
图3 Ricker子波通过不同检波器的输出结果

对于检波器a,b和c,Ricker子波的检波器输出信号出现零延迟,证明检波器a,b,c性能非常优秀,其中常规检波器c是一种理想检波器,因此,可以证明加速度计检波器的性能要优于常规检波器;常规检波器d和e的Ricker子波输出信号相较于输入信号,出现了较大的系统时延,而常规检波器f,g和h的Ricker子波输出信号相较于输入信号,更是出现了较大的系统时延,表明常规检波器的系统时延取决于许多因素,比如制造公差、野外测量条件以及噪声水平等。如果对常规检波器应用反褶积,可以降低常规检波器的系统时延,提高其性能。

与在频率域群延迟和相延迟的传递函数分析法相比,在时间域分析评估检波器性能的最大时延相关法对检波器性能差异的敏感度稍弱,这是因为群延迟在频谱范围内是非线性变化的,某种程度上抵消了其自身的影响。但这种抵消并不是理想的抵消,因为这种抵消在很大程度上依赖于信号的频谱特征。比较前述的8个检波器的输入、输出最大延迟可知,常规检波器对输入信号的失真是可见的,且其系统时延的范围为50～100μs。这与HAUER等[2]的基于传递函数分析法的结论类似,值得一提的是,对于地震采集系统,仪器允许的最大时延一般是10μs。

2 基于一致性函数的检波器性能评估方法

首先给出一致性函数的公式:

(6)

式中:Sxy(ω)是输入信号x和输出信号y的交叉谱密度(反映两个不同的随机序列在频率域变化上的相互关系),可以对信号x,y的互相关函数进行离散时间傅里叶变换(DFT)来求得,Sxy(ω)既包含相位信息,也包含振幅信息;Sx(ω),Sy(ω)分别是信号x,y的谱密度,只包含振幅信息,不包含相位信息。

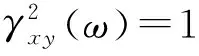
我们定义检波器的信噪比(RSN)为:

(7)

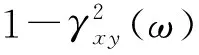
下面讨论如何利用一致性函数来评估检波器的性能。图4a和图4b分别为加速度计检波器a和常规检波器f的一致性函数曲线和基于一致性函数的信噪比曲线。以Ricker子波为输入,记为x,经过检波器a和f的输出结果分别记为ya,yf,构建一致性函数,评估两种检波器即常规检波器和加速度计检波器的性能。

从图4可以看到,因为常规检波器f存在共振现象,其一致性函数值一直低于加速度计检波器a的一致性函数值,直到频率为150Hz处。在频率为150Hz左右处,噪声较大,观察信噪比曲线,可以发现噪声量级与输入有效信号Ricker子波的量级基本相同;在低频部分,特别是在频率为1Hz以上,常规检波器f的一致性函数值存在一个尖锐的下降;在中部的频率范围内,常规检波器f的一致性函数值要明显低于加速度计检波器a的一致性函数值;而在频率为150Hz以上,噪声占据主导地位,两种类型的检波器的一致性函数值基本重合,代表其性能并没有什么不同。

图4 检波器a和f的一致性函数曲线(a)和信噪比曲线(b)

进一步研究基于一致性函数的检波器性能评估方法,我们选取常规检波器c作为评估对象,已知常规检波器c为理想检波器,没有参数漂移,这在现实中基本不存在,但可以基于一致性函数,比较这种理想常规检波器和加速度计检波器的性能。图5a和图5b 分别展示了加速度计检波器a和理想常规检波器c的一致性函数曲线及其信噪比曲线。

从图5可以看到,在低频1Hz以上的频率范围内,理想常规检波器c的一致性函数值要高于加速度计检波器a的一致性函数值,证明在这个频率范围内,理想常规检波器c的性能要优于加速度计检波器a,这归功于反褶积算子对常规检波器的处理,但是值得注意的是,我们并没有对加速度计检波器应用反褶积算子。本文中,我们设置预白系数α=0.1%(通常α=1.0%),应用一致性函数方法分别评估检波器a到检波器h等8个不同参数不同种类的检波器的性能,评估结果与应用传递函数分析法和最大时延相关法的评估结果相同,因此,基于一致性函数的检波器性能评估方法是有效的。

通过以上的分析,我们可以知道常规检波器和加速度计检波器的本质区别是常规检波器在油气勘探的地震信号带宽范围内存在共振现象,导致了输出信号存在非线性的相位改变,而加速度计检波器的共振频率远高于油气勘探的地震信号带宽范围,因此加速度计检波器输出信号的相位改变是极小的和线性的。

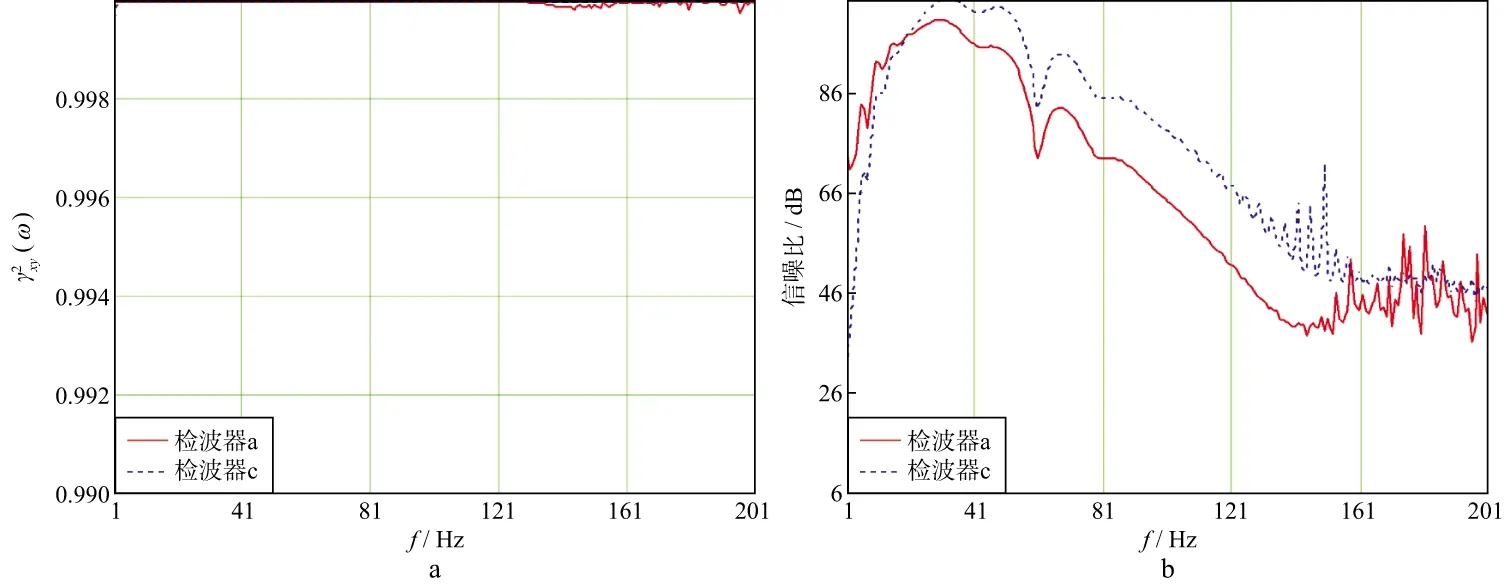
图5 理想常规检波器c和加速度计检波器a的一致性函数曲线(a)和信噪比曲线(b)

3 结论

基于一致性函数的检波器性能评估方法可以统一分析可能影响检波器性能的因素,比如制造公差、环境参数(温度、湿度)影响等,将振幅失真、相位失真、后处理调制以及影响信噪比的噪声等多个待分析变量统一为一个变量,即一致性函数值,绘制一致性函数曲线,直观、简明、全面地评估检波器的性能。该方法可与传递函数分析法以及最大时延相关法相结合,即先综合评价检波器性能,再利用传递函数分析法以及最大时延相关法得到对检波器性能差异的精确描述,实现对检波器性能全面、准确的评估。

致谢:首先感谢ION Geophysical Corporation和 Colibrys Incorporated允许此论文的发表,其次要感谢Phil Behn,Arjun Selvakumar,Howard Goldberg,Kedu Han和James Hereford在撰写论文期间的鼓励与支持。