独立性检验问题情景的数学等价刻画
2018-07-14李勇杨平王雁
李 勇 杨 平 王 雁
(1.北京师范大学统计学院 100875;2.北京日坛中学 100020)
数学抽象是数学的核心素养之一,其内涵是用已经掌握的数学知识描述问题情景本质,为进一步解决问题奠定基础.在教学过程中,常将数学抽象融入新知识的教学过程中,以熏陶学生的数学抽象能力.本文探讨在高中知识背景限制下分类变量独立性检验问题情景的数学抽象,研究该问题的数学等价刻画.
在人民教育出版社出版的普通高中课程标准实验教科书《数学选修2-3(A版)》中,以吸烟与肺癌是否有关系为问题背景介绍了独立性检验的基本思想与实施步骤,其出发点是:“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”.一个自然的问题是为什么会有这种等价关系?能否用学生们之前学习过的数学和概率知识刻画“吸烟与患肺癌没有关系”?
为了回答这些问题,需要引入必要的符号进行数学抽象.现在的研究对象是由人组成的有限总体Ω,在该总体上定义了两个变量,分别是吸烟变量X和肺癌变量Y,它们都是分类变量:对于总体中任何一人ω∈Ω,吸烟变量和肺癌变量的定义分别为

这样“吸烟与肺癌没有关系”的数学刻画就是“吸烟者中患肺癌的比例与不吸烟者中患肺癌的比例相等”,即
(1)

显然可以先获取所有个体的吸烟和肺癌变量数据,然后通过精确计算(1)式两端的比例得到问题的答案,这是一种纯数学的解答思路.但是在实际应用中,由于获取总体中所有个体变量数据的成本非常高,人们不得不考虑用部分个体数据来推断问题的答案是什么,这就需要确定判断的出发点和依据,即要从其它角度分析“吸烟与肺癌没有关系”的等价数学刻画,即(1)的等价刻画问题.
若能将(1)的左右两端都看成概率,就可以依据频率稳定于概率的思想,通过相应的两个频率是否接近推断 “吸烟肺癌没有关系” 是否成立.可从古典概率的角度看待(1)式两端的分式:由于总体Ω为有限总体,可以把它看成是古典概型的基本事件空间,那么用已经学习过的古典概率计算公式和条件概率的知识就可以得到
因此与“吸烟与肺癌没有关系”等价的条件概率刻画是

(2)
下面就以古典概型的视角看待总体Ω:在总体中任取一人,就不能预知吸烟变量的取值,也不能预知肺癌变量的取值,他们的随机变化规律由古典概型所决定.
从“吸烟与肺癌没有关系”的条件概率刻画,可以进一步探讨“吸烟与肺癌没有关系”的条件分布列的等价刻画.事实上,由(2)可知

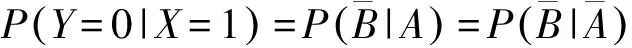
=P(Y=0|X=0),
因此在X=1条件下Y的条件概率分布列

Y01在X=1条件下Y的条件概率PY=0|X=1()PY=1|X=1()
等于在X=0条件下Y的条件分布列

Y01在X=0条件下Y的条件概率PY=0|X=0()PY=1|X=0()
这就是“吸烟与肺癌没有关系”的条件分布列刻画.
依据条件分布列刻画,可以将“吸烟与肺癌没有关系”解释为:吸烟变量的取值不会影响肺癌变量的条件概率分布列,即吸烟变量的取值不会影响肺癌变量随机变化规律.这样,对于普查数据,也可以用条件概率分布列或密度图的对比来解答两个分类变量是否有关系问题;对于好的样本观测数据,频率会稳定于概率,可以借助于频率条形图来推断吸烟与肺癌是否有关系,以及解答吸烟是否更容易导致肺癌等问题.
相对而言,概率比条件概率更简单,若能直接用概率刻画“吸烟与肺癌没有关系”,就会提高研究效率,下面我们讨论“吸烟与肺癌没有关系”的概率刻画问题.
如果(2)成立,则有

注意到
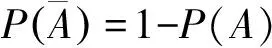
=P(B)-P(AB),
可得
P(AB)(1-P(A))
=(P(B)-P(AB))P(A),
整理可得
P(AB)=P(A)P(B)
(3)
即事件A和B相互独立.
而由事件A和B相互独立可得
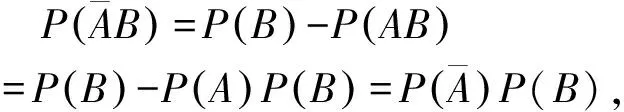
P({X=u}∩{Y=v})=P(X=u)P(Y=v)(4)
即事件{X=u}和事件{Y=v}都相互独立,此时称分类变量X和Y相互独立.因此(3)等价于(4), 即等价于X和Y相互独立.


即(2)成立.因此(2)等价于分类变量X和Y相互独立,也等价于(3).为讨论方便,称(3)为“吸烟与肺癌没有关系”的概率刻画,称(4)为“吸烟与肺癌没有关系”的独立性刻画.
综前所述,可以从不同的角度刻画“吸烟与肺癌是否有关系问题”:从纯数学的角度出发,得到了该问题的等价刻画(1);从古典概型的角度出发,得到了该问题的条件概率刻画(2)、概率刻画(3)和独立性刻画(4).这四种刻画都有各自的特点和应用价值,下分别加以总结.
1.数学刻画(1)不需要任何概率统计知识,是该问题情景的数学本质描述.直接从数学刻画出发,可以利用普查数据解答所关心的问题,但在实际应用中普查的成本成为能否应用这种解答方法的关键.
2.产生条件概率刻画(2)的关键在于我们在总体Ω上构建了古典概型,使得X和Y都成为随机变量.这种刻画比数学刻画更为复杂,好处是可以通过条件概率知识解释两个变量之间有关系或者没有关系的含义,也为利用频率稳定于概率的思想推断问题结论奠定基础.
3.在条件概率刻画的基础上,利用概率知识建立了概率刻画(3).概率刻画的好处是更容易应用频率稳定于概率的思想进行推断,以解决普查成本过高的问题.
4.在概率刻画的基础上,利用概率知识建立了独立性刻画.独立性刻画可以用来解释两个变量之间有关系或者没有关系的含义:两个变量之间有关系等价于它们之间不是相互独立;两个变量之间没有关系等价于它们之间相互独立.特别地,独立性刻画还解释了人们将这类问题称之为独立性检验问题的原因.
通过对于“吸烟与肺癌是否有关系问题”的四个等价刻画的探讨,使我们认识到:对于给定的问题,可以从不同的角度去刻画和研究,以缩减问题研究成本和更好地认识问题的本质;通过这些探讨,可以使学生反复体会以问题为导向的数学抽象的过程,培养他们的数学抽象能力.
