我国初中几何教科书中勾股定理证明方法编排之变迁(1951—2000)*
2018-07-14李春兰
庞 月 李春兰
(内蒙古师范大学数学科学学院 010022)
勾股定理被称为千古第一定理,它揭示了直角三角形的三条边之间的关系,一直以来受到人们的广泛关注.迄今为止,知道该定理已有400多种证明方法.各套初中几何教科书中勾股定理章节中证明方法的编排代表了我国各时期几何证明的教学理念.初中阶段几何证明的学习是知识的灵活运用、思维的分析和综合的过程,因此有必要从学习几何证明的角度培养学生的逻辑推理能力.Mammana&Villani指出:如果学生在初中阶段没有学会几何证明的话,那么,他们可能永远失去了这个机会.**基金项目:本文是“内蒙古师范大学研究生科研创新基金资助项目(课题主持人:庞月)的研究成果”.**本文通讯作者:lichunlan@imun.edu.cn①转引自:鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:280数学大师陈省身在接受采访时谈到对于推理证明的看法:“学生应该学会推理,推理很要紧,推理不仅在数学,在其他学问里也是要用到的.”*周雪梅.中美几何教材内容中的推理与证明的比较研究[C].上海:华东师范大学,2012:3
证明是一种推理或者提出论据以说服某个人接受一种信念*(美)贝尔.中学数学的教与学[M].许振声,译.北京:教育科学出版社,1990:339,察古观今,“证明”始终作为培养学生逻辑思维能力的重要手段,是数学学习的重中之重,是初中生必须掌握的一项基本技能.勾股定理的教育价值不仅在于其丰富的文化思想,它还是培养学生几何推理证明的典型素材.自20世纪以来,几何教科书中对证明的要求以及证明内容的编排时移势迁.勾股定理始终是几何教科书中的经典内容.故本文以1951-2000年人民教育出版社出版(以下简称“人教版”)的10套全国通用中学数学教科书中“勾股定理”的证明方法为研究对象,对不同时期各套教科书中的勾股定理证明方法之编排进行研究,阐述不同版本中“勾股定理”证明方法的编排特点.但由于1966—1976是文化大革命的十年,教育系统遭到破坏,没有全国统编的数学教科书,因此该阶段教科书在本文不做研究.
1 人教版数学教科书中“勾股定理”证明方法编排概述
1.1 培养逻辑应用能力本位时期(1951—1963)
建国初期,教育部提出“以苏为鉴”的教育方针,并要求几何教学的目标应是发展学生的逻辑的思维和对于空间的想象力,并使他们运用所学到的知识去解决实际问题:进行实地测量,测定各种建筑物的表面积和容积等等.在这一方针的指导下,国家先后共颁布五个教学大纲,人教社分别出版了全国通用的第1套(1951年)、第2套(1954年)和第3套(1960年)初中几何教科书.其中第2、3套初中几何教科书中未编排勾股定理内容.*根据1954年《中学数学教学大纲》(修订草案),将“勾股定理”内容编排在由余元庆、奚今吾、管承仲、吕学礼编写的《高级中学课本平面几何》(二册),以供高中一年级学生学习.勾股定理则出现在第二分册的第三章“三角形中及圆中各线段间的相互关系”中,证明方法是比例中项法
1950年,人民教育出版社成立后,根据教育部颁发的《数学精简纲要(草案)》对旧课本进行修订、改编,出版了《初级中学平面几何课本二册》(上册1951年3月原版,下册1951年8月原版),即为第1套初中几何教科书,以满足全国开学后之需要.该套书在编辑大意中写到:“本书对于定理的证明,理由叙述的很少,这是因为留作教学时教师们便于随时发问使读者自行思索.”
在该套书中,勾股定理章节编排在下册的第三章§220中,关于勾股定理的内容阐述及证明方法如下:
定理直角三角形的两条直角边的平方的和等于它的斜边的平方.
[假设]△ABC的C角是直角,∠A,∠B和∠C所对的边分别是用a,b和c表示.
[终结]a2+b2=c2.
[证明]在下图中作CD⊥AB,设AD=d则DB=c-d,由AB∶AC=AC∶AD和AB∶CB=CB∶DB,
即c∶b=b∶d和c∶a=a∶c-d.

∴b2=cd和a2=c(c-d)=c2-cd,两式相加就得a2+b2=c2.
在该套教科书中直接给出勾股定理的表述,并用比例中项的方法证明,比例知识是初中算术的主要内容,课标要求比例的运算道理是初中教学算术的主要教学目的.运用比例中项法是在学生已掌握原有知识的基础上从图形出发,数形结合,以分析法证明勾股定理.这不仅与其他科目相辅相成,符合学生的知识结构特征,而且该方法是各套教科书中最为简洁的一种.在证明之后又介绍了勾股定理的另外两个名称的由来,即毕达哥拉斯定理和商高定理,并重视对该定理的应用,介绍了如何利用一根绳子测量直角,同时说明了这一方法我国在很早就已应用.
1.2 培养逻辑推理能力本位时期(1963—1999)
随着国际上数学教育现代化的兴起,我国进入了数学教育改革的激进时期.1963年教育部颁布的《全日制中学数学教学大纲(草案)》中第一次明确提出要培养学生的“正确而且迅速的计算能力、逻辑推理能力和空间想象能力”.这一提法,将逻辑推理能力放在了突出的位置,并正视了几何证明的重要性.在此后的30余年的时间内,培养学生的三大能力成为数学主要的教学目的,并先后出版了第4至9套几何教科书.
(1)第4套几何教科书
1963年的教学大纲要求:“中学几何虽与欧式几何不同,但便于培养他们推理论证的能力,也应该在学生能够接受的条件下,力求逻辑的严谨性.”*课程教材研究所.20世纪中国中小学课程标准教学大纲汇编(数学卷).[M].北京:人民教育出版社,2001:437根据这一纲领,人教社出版了第4套全国通用几何教科书《初级中学课本平面几何(暂用本)》第一册(1963年第2版)和第二册(1964年第2版).勾股定理内容出现在第一册的第五章“多边形的面积”中,§5.8直接给出勾股定理的表述,如下:
5.8勾股定理 我们把直角三角形的两条直角边分别叫做勾和股,把斜边叫做弦(如图).直角三角形的勾、股、弦之间,有下面定理所说的关系.

勾股定理直角三角形弦上正方形的面积,等于勾上正方形面积与股上正方形面积的和.
已知:ABC是直角三角形,BCDE是它的斜边BC上的正方形,ABFG和ACHK分别是它的直角边AB和AC上的正方形,求证:正方形BCDE的面积=正方形ABFG的面积+正方形ACHK的面积.
证明:作AL⊥BC交BC于M、交ED于L;那么正方形BCDE被分成两个矩形.所以
正方形BCDE的面积=矩形BMLE+矩形MCDL的面积.
连结AE和CF.由于矩形BMLE和△ABE有公共的底BE和相等的高(都等于平行线AL和BE间的距离);所以矩形BMLE的面积=△ABE的面积×2.
又由于正方形ABFG和△FBC有公共的底FB和相等的高(都等于平行线GC和FB间的距离);所以正方形ABFG的面积=△FBC的面积×2.
另一方面,在△ABE和△FBC中,AB=FB,BE=BC(正方形的四条边都相等),∠ABE=∠FBC(都等于∠ABC与一个直角的和);∴△ABE≅△FBC,从而△ABE的面积=△FBC的面积.∴矩形BMLE的面积=正方形ABFG的面积.用同样的方法,连结AD和BH,可以证明矩形MCDL的面积=正方形ACHK的面积.∴正方形BCDE的面积=正方形ABFG的面积+正方形ACHK的面积.
根据勾股定理可以知道,如果直角三角形的勾、股、弦分别是a、b、c,那么a、b、c之间有下面的关系:c2=a2+b2.
勾股定理这一章节采用“定理”—“已知”—“证明”的编排结构,结构严谨,直截了当.证明过程用了一页篇幅之多,是各套教科书中证明过程最为严密的一套,同时,也明确了欧几里得公理体系的地位.在欧几里得证法之后,又以“赵爽弦图”辅助证明,阐述较简洁,仅说明了这种方法记载于赵爽的《勾股方圆图注》中,利用面积相等法即可证明勾股定理,说明了我国古代数学的辉煌成就.同时,该章节的不足之处在于勾股定理的表述并不明确,仅说出直角三角形三边的几何关系,即“弦上正方形的面积,等于勾上正方形面积与股上正方形面积的和”,容易造成学生理解误区,故在之后的数学教科书中未再采取该表述方式.
(2)第5套几何教科书
1978年颁布的《全日制十年制学校中学数学教学大纲(试行草案)》是文革后的第一个教学大纲,并以此发行了《全日制十年制学校初中课本(试用本)数学》(6册),这是建国以来第一套混编通用数学教科书.勾股定理内容位于第三册(1978年第1版)的第四章“直角三角形”中,§2.17勾股定理编排方式如下:
如图,三角形ABE、BCF、CDG、DAH是四个全等的三角形,它们的两条直角边分别等于a和b,斜边等于c,把这四个直角三角形拼成如图所示的四边形ABCD,那么四边形ABCD的面积等于这四个直角三角形的面积与四边形EFGH的面积的和.

∵AB=BC=CD=DA=c,
∠DAB=∠EAB+∠HAD=∠EAB+∠EBA=Rt∠,
同理,∠ABC=∠BCD=∠CDA=Rt∠,
∴ 四边形ABCD是正方形,它的面积等于c2.
∵EF=FG=GH=HE=b-a,∠HEF=∠EFG=∠FGH=∠GHE=Rt∠,
∴ 四边形EFGH是正方形,它的面积等于(b-a)2.
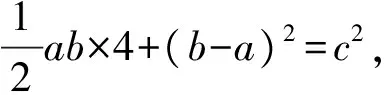
即a2+b2=c2.
勾股定理在直角三角形中,斜边的平方等于两条直角边平方的和.
该套教科书,以我国《周髀算经》中“勾三股四弦五”的记载引入,利用“赵爽弦图”的方法证明,做到从特殊到一般的归纳推理形式.这是在教科书中首次使用以“赵爽弦图”进行推理证明,并在脚注中注明了这个方法出自于赵爽的《勾股方圆图注》.但是“赵爽弦图”的拼图思路及拼图过程并没有阐述,这样的教学方式固化了学生的思维,限制了学生自由探索勾股定理奥秘的思路.这是东方数学教学的一大弊端.教科书的编写首次扩大了公理体系,勾股定理的逆定理首次被编排在这一章节中,并用反证法予以证明,这是培养学生的逻辑思维能力的强有力手段.足以见得,对几何证明的重视程度正在不断提高.在章末,传说中的毕达哥拉斯证明勾股定理的方法以习题的形式出现,但遗憾的是,并未介绍这一证法的名称及由来.
(3)第6、7套几何教科书
第7套初中几何教科书(1989年)是第6套初中几何教科书的改编本,因此关于勾股定理内容编排并无差异,在此以第6套初中几何教科书为例,阐述勾股定理的证明方法.
1982年4月《全日制六年制重点中学数学教学大纲(征求意见稿)》中指出:教学中要积极启发、引导学生进行归纳、演绎、分析、综合、抽象、推广,使学生形成正确的数学概念,理解法则定理以及各种方法.*课程教材研究所.20世纪中国中小学课程标准教学大纲汇编(数学卷)[M].北京:人民教育出版社,2001:488在这一方针指导下, 1983年人民教育出版社数学编辑室编写了《初级中学课本几何》(2册),勾股定理被编排在第一册的第五章“面积、勾股定理”的第二节.
定理直角三角形两条直角边a、b的平方和,等于斜边c的平方.
a2+b2=c2
已知,在Rt△ABC中,AB=c,BC=a,CA=b.求证:a2+b2=c2.
证明:如图乙那样,取四个与Rt△ABC全等的三角形,放在边长为a+b的正方形内,得到边长分别为a、b的正方形Ⅰ、Ⅱ.

再将同样的四个直角三角形,如图丙那样放在边长为a+b的正方形内,这时,得到的四边形Ⅲ也是正方形,并且边长等于△ABC的斜边c.
比较乙、丙两个图形,正方形Ⅰ、Ⅱ的面积的和a2+b2与正方形Ⅲ的面积c2都是同一正方形面积与4倍△ABC面积的差,所以a2+b2=c2.
1983年版教科书中勾股定理的表述,首次将文字与符号融为一体,使定理表述的更加形象具体.证明方法采用的是上册练习题中的毕达哥拉斯证法,通过三个小正方形的面积关系,得出定理.在证明过程中,第一次不再采用罗列步骤的形式,而以说理的方式完成证明.这是学生在熟练掌握证明方法及步骤之后,以培养学生分析能力为主要目的,证明步骤可以简略.这种方式减少了符号描述,抽象性降低,易于理解.欧几里得证法在例题中以证明题的形式出现,相比于第4套教科书中的证明步骤,较简略,并说明这种方法是欧几里得在《几何原本》中的证明方法.“赵爽弦图”在课后习题中也以证明题的形式出现,并说明了证法的由来.三种证明方法异曲同工,丰富了学生证明数学问题的方法和手段.
(4)第8、9套几何教科书
第8套(1990年)和第9套(1993年)初中几何教科书关于勾股定理内容编排并无差异,在此第8套初中几何教科书为例,阐述勾股定理的证明方法.
《义务教育三年制初级中学教科书几何(实验本)》(第一册、第二册1990年第1版,第三册1991年第1版)是根据1988年颁布的《九年义务教育全日制初级中学数学教学大纲(初审稿)》编写的.课标中要求:“使学生能够用直接证法进行简单的推理,初步培养观察、分析、综合、抽象、概括等能力以及分类、类比等思想,了解反证法,从而提高学生的逻辑思维能力.”*课程教材研究所.20世纪中国中小学课程标准教学大纲汇编(数学卷)[M].北京:人民教育出版社,2001:568勾股定理证明内容设置在第二册§3.17中,具体编排如下:
勾股定理直角三角形两直角边a、b的平方和,等于斜边的平方.
a2+b2=c2
下面我们用拼图的方法来证明.
用8个全等的直角三角形.设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像图中那样拼成两个正方形.
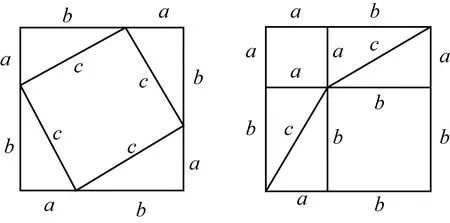

这一时期的教科书,呈现的勾股定理的证明方法更加多样化.以毕达哥拉斯的证法为主要的证明方法.在习题中,“赵爽弦图”以证明题的形式出现.在课后阅读部分,介绍了证明勾股定理的方法已经有几百种,并呈现了刘徽的青朱出入图和美国总统加菲尔德证明勾股定理的图形.力求学生在学会勾股定理的前提下,能从不同思维角度入手,解决同一问题,提高学生的逻辑思维能力.勾股定理的逆定理共给出两种证明方法,不再拘泥于反证法,而是向合情推理过渡.先阐述勾股定理的逆定理的定义,然后结合已积累的知识,概括抽象出猜想,最后以实例进行论证.
1.3 培养逻辑推理思想本位时期(2000—至今)
2001年7月颁布的《全日制义务教育数学课程标准(实验稿)》中提出教育目的应是进一步培养运算能力,发展思维能力和空间观念,思维能力主要指:会观察、实验、比较、猜想、分析、综合、抽象和概括;会用归纳、演绎和类比进行推理,会合乎逻辑地、准确地阐述自己的思想和观点.自此,几何证明教学中的要求不再局限在证明的方法、步骤,而是在证明的过程中严谨、合理的证明思想.
(1)第10套数学教科书
根据实验稿的课程标准,人教社于2004年出版了第10套初中几何教科书,注重对证明本身的理解,而不追求证明的数量和技巧.在该套教科书中,勾股定理内容设置在八年级下册第十八章中,由学生探究一般直角三角形三边关系引出勾股定理,并用“赵爽弦图”证明.具体编排如下:
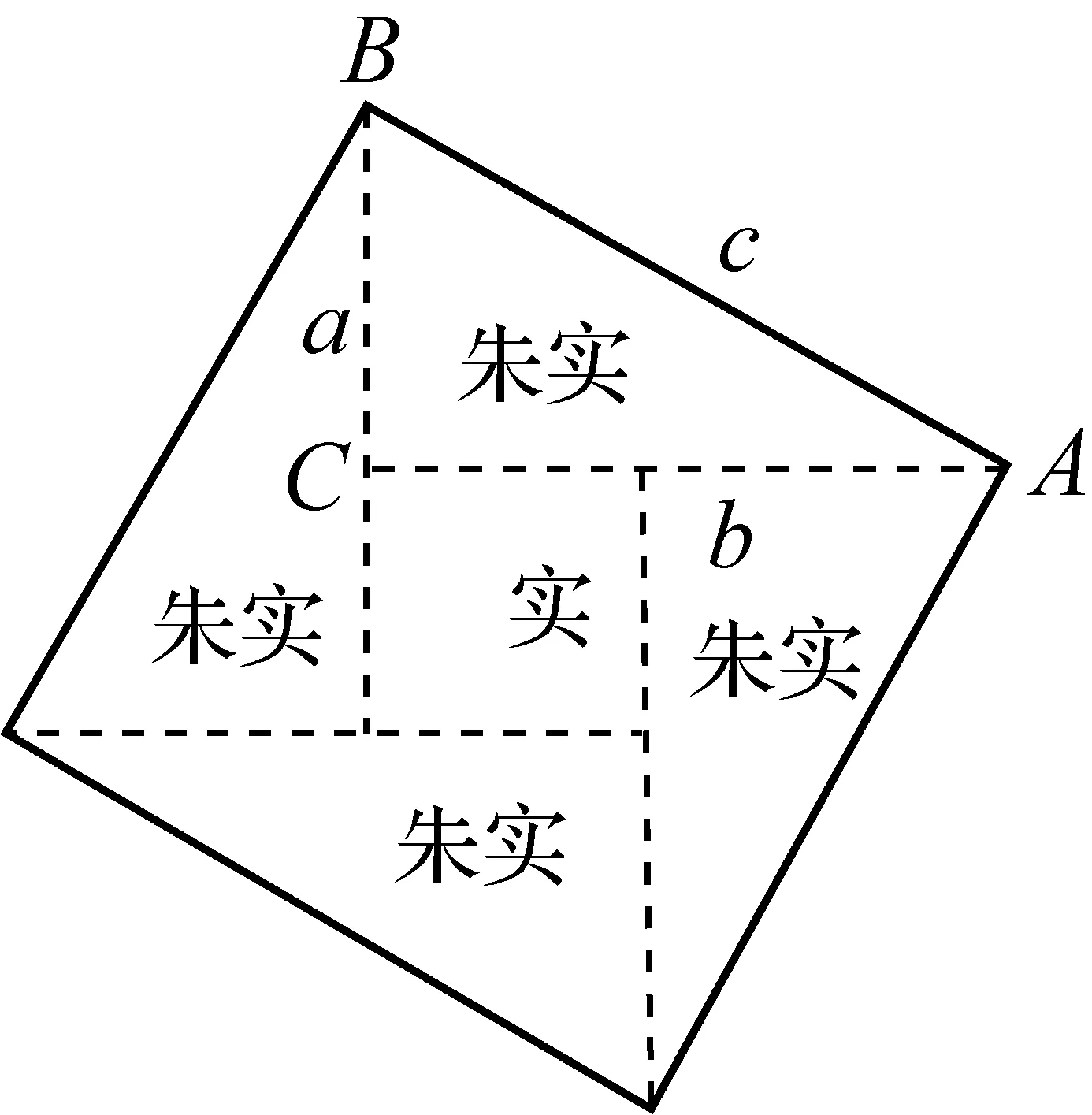
命题1如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
证明命题1的方法有很多,下面介绍我国古人赵爽的证法.
赵爽利用弦图证明命题1的基本思路如下:把边长为a,b的两个正方形连在一起,它的面积是a2+b2;另一方面这个图形可分割成四个全等的直角三角形(红色)和一个正方形(黄色).把图(1)中左、右两个三角形移到图(2)中所示位置,就会形成一个以c为边长的正方形图(3).因为图(1)与图(3)都由四个全等的直角三角形(红色)和一个正方形(黄色)组成,所以它们的面积相等.因此,a2+b2=c2.
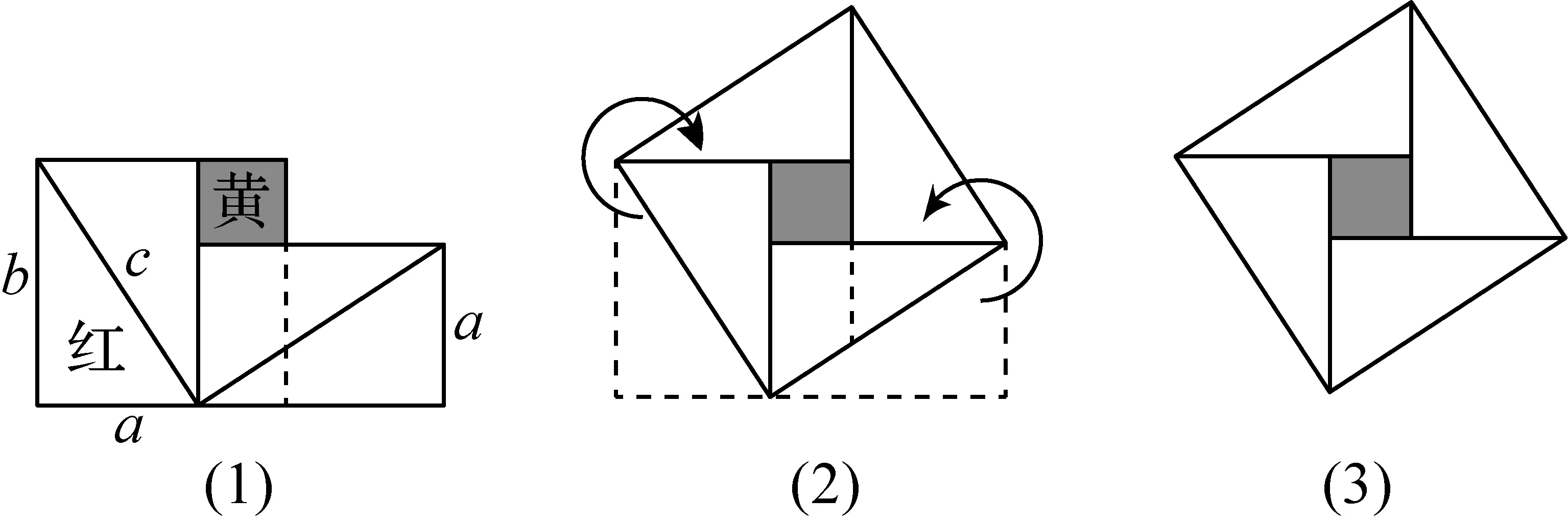
这样我们就证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称为勾股定理.
在该套书中,勾股定理自成一章,并配有大量习题,增强对证明意义和必要性的重视.该章节中,虽然继续沿用“赵爽弦图”为主要的证明方法,但史料介绍是最细致生动的一套,使之明确证明方法的由来.在结构编排上也有所不同,该套教科书仅阐述了证明的思路,进而得出结论,并没有证明过程,不同于以前版本的教科书而设置“证明”的字样.可以看出,该套教科书更重视证明思维的培养,明确证明的思路与过程.在课后阅读部分中,毕达哥拉斯证法、“赵爽弦图”的另一种证法以及美国总统加菲尔德的证法的精彩呈现,是学生进一步学习勾股定理的素材.勾股定理及其逆定理的证明是作为探究活动的自然延续,使学生了解合情推理与演绎推理是相辅相成的两种推理形式,并且证明过程及其表述符合逻辑,清晰而有条理.
1.4 小结
勾股定理的核心即直角三角形三边之间的关系,在10套全国通用的几何教科书中,共用了4种方法对其进行证明,分别是比例中项法、欧几里得证法、毕达哥拉斯证法以及“赵爽弦图”的证明方法.在课后阅读及练习题中共提及7种证法,除以上证明方法外,还有美国总统加菲尔德的证法,刘徽的“青朱出入图”以及弦图的另一种证法,用以辅助证明、加深理解,详情见表1.各个时期对勾股定理证明的方法符合时代特征,发展学生逻辑思维的广阔性和灵活性是几何证明的共同要求.

表1 “人教版”10套初中几何教科书中勾股定理证明方法汇总
比例中项法仅在第1套教科书中使用,其原理是射影定理,被奉为是历来的经典之作.后来算术科目的消失,成为勾股定理证明不再采用比例中项证法的主要原因.欧几里得证明方法和“赵爽弦图”是东西方数学史上璀璨的明珠,两者相较,欧几里得证法采用的是分析法,执果索因,而“赵爽弦图”则为综合法,由因导果,展现了文化差异下的不同思维方式,是各自文明中思想传统的直接体现,是中国的“数形统一”和古希腊“算术与几何证明分离”传统的思维碰撞.在各套数学教科书中,毕达哥拉斯的证法与“赵爽弦图”的证法是出现次数最多的两种证明方法,其实质皆为拼图法,即利用直角三角形拼成不同的图形,通过面积相等得出勾股定理.拼图法与其他方法相比更能联系学生生活实际,从已有的知识出发,启发、引导学生进行归纳、推理.两种方法异曲同工,而毕达哥拉斯证法逐渐被“赵爽弦图”所取代,培养学生爱国主义情怀和增强民族自豪感的的教学目标可能是主要原因.
2 勾股定理证明方法编排变迁特点分析
2.1 “赵爽弦图”的证明方法由辅助证明演变为全面阐述
第4套教科书中,在欧几里得证法之后,引入了“赵爽弦图”的方法辅助证明勾股定理,作为加深理解之用.从第6套教科书至第9套教科书,“赵爽弦图”都在练习题中以证明题的形式出现.在这几套教科书中,弦图被介绍为“勾股方圆图”,原因是赵爽在《勾股方圆注》中证明了勾股定理.第5和10套数学教科书则在正文中利用大量的篇幅介绍了古人赵爽、“赵爽弦图”的由来,以及如何利用“赵爽弦图”证明勾股定理.“赵爽弦图”是我国历史上数学繁荣发展的表征,在证明过程中融入数学史,是激发学生对证明的兴趣的基本素材.同时,足以见得,在培养学生证明能力的同时,注重对证明兴趣的培养.
2.2 欧几里得证法由正文的全面阐述演变为例题证明
古希腊数学家欧几里得曾把勾股定理编写在他所编著的《几何原本》一书中,并对其证明,证明的方法称为欧几里得证明方法.在第4套教科书,勾股定理这一章节中,利用欧几里得的证法来证明勾股定理.该方法是纯粹几何图形之间的关系,不涉及数,证明是及其严格的,但遗憾的是原书中并没有欧几里得的相关介绍.第6、7套几何教科书中,欧几里得证明方法以例题的形式出现,给出图形,证明直角三角形三边关系.由于是例题,证明过程仅呈现主要步骤,简洁明了,并介绍了这种方法的由来.欧几里得证法其核心是使用演绎法证明,将数学的严谨性和抽象性相结合,但后来欧几里得证法在教科书中的逐渐消失,也是几何学习不再过度强调严谨性的重要表征.
2.3 拼图法逐渐成为证明勾股定理的主要方式
第1套和第4套的几何教科书分别采用比例中项法和欧几里得证明方法,采用纯演绎推理的方式.除此之外,则以拼图法为主要证明方法,在理性证明的同时兼用实用性证明.第6—9套教科书中采用8个三角形构造出两个不同正方形,利用其面积相等的方法来证明勾股定理.第5套和10套几何教科书则直接将4个三角形拼补成“赵爽弦图”,利用不同的面积表示方法进行证明.证明的过程也不再是严格的三段论推理,加入了说理的方法,语言更加简明扼要.图形的表示也不仅只是静态的数形结合而是生动形象的描绘了拼图的过程,感受数学实证的过程.
3 启示与建议
纵观我国50年初中几何教科书中勾股定理证明之变迁历程,可以看出,各时期几何证明的教学均适应当时的社会发展和教学大纲要求,并逐步受到重视.但方兴未艾,未来数学教科书应从历史的发展中择善而从,为未来数学学科的发展做好准备.故回顾人教社出版的10套教科书,在勾股定理章节编排的建设上,提出以下建议.
3.1 编排体系应力求严谨
纵观10套数学教科书的发展史,自第4套教科书出版以来,每每受到许多教师的赞誉,称赞“六三本好”,认为其优点在于内容充实,理论、文字严谨,编排科学,讲解细致,例习题配备合理、充足*李润泉,陈宏伯,蔡上鹤等.中小学数学教材五十年(1950—2000)[M].北京:人民教育出版社,2008:231,即编排体系合理、严谨.严谨合理不仅体现在证明过程中,还表现在知识的呈现方式,结构体系的设计,素材的选配,证明方法的选择等方面,正如胡敦复所说:“结构不必宏达,见地需独到,材料不妨浅近而说理务宜精详.”故此,在编排体系上,之后的勾股定理章节编写可从第4套教科书中吸取优点,当然,编排内容也应符合现代的社会发展,与时俱进.
3.2 理性证明和实验性证明能力的培养并重
证明贯穿于数学教学的始终,证明能力的形成和提高需要一个长期的、循序渐进的过程.义务教育阶段要注重学生思考的逻辑性,不要过分强调推理的形式.F.H.Bell在1978年将证明分为实验性证明和理性证明,应使这两种证明方式相辅相成.在勾股定理章节甚至现今的几何教科书中,实验性证明的培养并不受到重视.然而两种证明形式是既对立又统一的,数学证明的理解与接受需要实验性证明的帮助,这是以理解为价值取向的数学教学的需要,证明结论的正确性则需要理性证明的确认,单一的理性证明方式能够有效地培养学生的逻辑思维能力,但实验性证明与理性证明相结合的手脑合一的方式是学好证明更有效的途径.故在勾股定理这一章节,证明方法应兼顾实用性证明.
3.3 证明方法的编排应注重证明思想的差异性
勾股定理作为初等几何的著名定理,现今的证明方法已有400余种,这种“多”不仅体现在数量上还有证明思路、方法上,不同的证明方法是证明思想差异的产物.要培养学生多角度的证明思维,应将勾股定理证明方法按照证明思路分门别类,使学生更多的了解不同思想实质下的证明方法.这不仅是挑战学生思维的极限,还能够将平面几何中的常见证明思路结合起来,理解不同证明方法间的横向关系,达到融会贯通的目的.但因数学教科书篇幅有限,不可能将各种证明思路均呈现,但有些经典的证明还是要给出来的.其中我国数学史上经典的“赵爽弦图”证法和最具严谨性的欧几里得证法皆是学生锻炼逻辑思维能力的最好素材.因此,以上两种证法应被编排在勾股定理章节中,其他证法应根据时代需求,按照证明思路进行适当编排.
