三跨连续下承式梁-拱组合体系桥抗震性能 及其参数影响规律研究
2018-07-14熊柏林徐略勤李建中
熊柏林 徐略勤,* 李建中 王 龙
(1.重庆交通大学土木工程学院,重庆 400074; 2.同济大学土木工程防灾国家重点实验室,上海 200092)
0 引 言
梁-拱组合体系将梁和拱两种构件巧妙组合在一起,协作承受荷载,既能发挥各自的优点,又能克服各自的缺点,是一种美观且经济的桥型[1]。梁-拱组合桥通常属于外部静定、内部高次超静定的结构体系,上部结构刚度和质量均很大,而下部结构常采用常规的墩柱构造,因此在地震中下部结构需要承担很大的惯性力,对抗震不利[2]。这其中三跨连续下承式梁-拱组合桥的抗震问题尤其突出,其原因在于:传统连续梁桥的主梁惯性力往往集中在固定墩上,对抗震不利,而三跨连续下承式梁-拱组合桥的上部结构刚度和质量均更大,对固定墩的抗震更加不利,而且上部梁-拱组合结构本身节点众多,刚度突变处较多,也容易形成潜在抗震薄弱环节。
目前,相对于静力性能方面的研究,梁-拱组合体系桥抗震性能的研究较滞后,开展得也较晚。Felber等[3]通过实验修正的方法对老Port Mann桥所进行的模态分析算是较早的动力性能方面的相关研究成果之一。近年来,随着我国基建的快速发展,对梁-拱组合体系桥抗震性能的关注也逐渐增多,如研究摩擦摆支座、速度锁定装置在铁路连续梁-拱组合桥中的减隔震效果[2,4],评估梁-拱组合体系桥在设计地震下的抗震性能[5-7]等。从现有研究成果来看,目前国内对梁-拱组合体系桥抗震性能的研究仍主要为工程建设提供咨询,研究的宽度和深度受到一定的拘束,且很多研究的对象为单跨梁-拱组合桥,其结构体系相对更简单。此外,针对梁-拱组合体系桥中的诸如拱轴线、梁拱刚度比等重要参数[8]的研究也很少在抗震层面上展开。
本文以某新建的三跨连续下承式梁-拱组合体系桥为背景工程,首先基于能力/需求法对桥梁的抗震性能进行评估,然后围绕矢跨比、拱梁相对刚度比等关键结构设计参数对桥梁抗震性能的影响进行参数分析,以期为同类桥梁的抗震设计提供参考。
1 工程与分析模型
1.1 桥梁概况
某在建市政桥采用梁-拱组合体系结构,设计全宽为40 m,桥跨布置为(30+80+30) m。主跨为刚性系杆刚性拱,两个边跨处设置飞燕,拱轴线为二次抛物线,矢跨比为1/4。拱肋采用等截面矩形,肋高2.0 m,宽1.8 m。系杆亦采用等截面矩形,高1.8 m,宽2.0 m。每片拱肋设间距4.0 m的吊杆17根,吊杆由φ5 mm镀锌平行钢丝组成。全桥共设4道直径为1.0 m的圆形钢管风撑。端横梁、中横梁及跨中横梁高度均为1.60~1.743 m。桥墩采用实体式墩身,下设承台接桩基础。每个桥墩下设8根桩基础,桩径2.2 m,按摩擦桩设计。主桥支座采用GPZ(II)型盆式橡胶支座,其中2#墩为固定墩,其余墩纵向可活动。桥梁立面布置如图1所示。

图1 桥梁立面布置图(单位:m)Fig.1 Elevation view of the bridge (Unit:m)
1.2 分析模型
采用SAP2000建立分析模型,其中主桥部分如图2所示。拱肋、风撑、横梁、桥墩等均采用空间梁单元模拟;桥面板采用平薄壳单元离散为空间结构;吊杆采用桁架单元模拟;桩-土共同作用采用6×6集中土弹簧模拟;盆式支座的活动方向考虑摩擦效应,采用非线性Wen单元模拟。为了考虑拱肋与风撑等构件的二阶效应以及吊杆的非保向力效应,非线性时程分析工况计入P-Delta效应,并采用直接积分法进行运算。在主桥左、右侧各建一联引桥,以考虑边界联的影响,图2为图片清晰度的原因未将其显示出来。
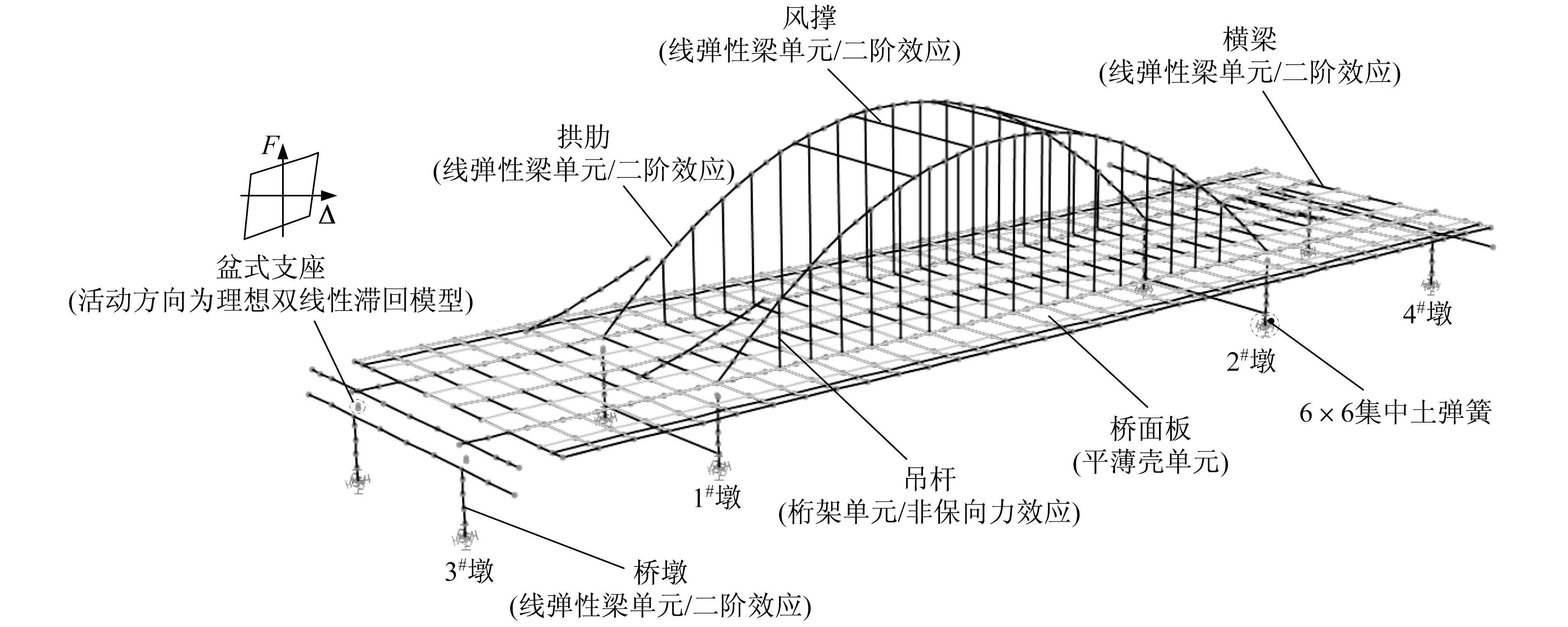
图2 全桥动力分析模型Fig.2 Dynamic analysis model of the whole bridge
1.3 地震动输入
根据地震安评报告,罕遇地震对应的峰值加速度为0.25g。地震动输入有两类:其一是安评提供的7条人工波;其二是3条实际地震记录,并采用小波变换来匹配场地设计反应谱,匹配情况如图3所示。采用纵向+竖向、横向+竖向的地震输入方式,其中人工波的竖向地震根据细则[9]采用水平地震折减的方式获得;实际波的竖向地震直接采用实际竖向地震记录。

图3 地震动Fig.3 Ground motions
2 抗震薄弱环节的识别
本文采用桥梁关键构件的能力/需求作为桥梁的抗震评价指标。对于钢筋混凝土构件来说,每个截面均存在初始、等效和极限抗弯能力(分别对应无损伤、可修复损伤和局部破坏三个状态),详见文献[10]。在确定桥梁抗震薄弱环节时,按照细则[9],将等效抗弯能力作为构件的抗震能力。
图4为在设计罕遇地震0.25g作用下各主要构件的抗震评价指标。在评价指标的计算中,抗震能力采用的是表1中数据,即按照罕遇地震对应的最不利轴力组合值计算得到的抗弯能力(在后文IDA分析中,抗弯能力同样根据各个PGA对应的最不利轴力组合值计算,限于篇幅,本文仅列出了罕遇地震下的损伤指标)。由图4可知,人工波和实际波的结果基本一致。在纵向+竖向地震下,只有1#墩左、右墩底的抗震富余最大,能力/需求达39.63~44.51;拱脚、1/4拱和2#墩(固定墩)的抗震富余量最小,接近临界线,因此是抗震薄弱环节。在横向+竖向地震下,抗震薄弱环节主要出现在拱脚、1#墩右墩底和2#墩右墩底,均接近抗震临界线。由于在横桥向单向支座放在右侧,因此同一个墩处,右侧墩柱的抗震性能明显更差。
限于篇幅,后文将以拱脚、1/4拱、1#和2#墩的右墩为例,对桥梁抗震性能及其参数影响规律进行分析。
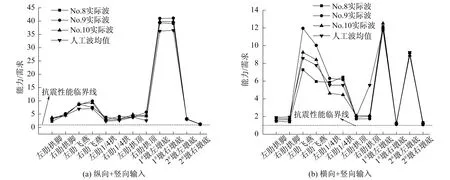
图4 主要构件抗震评价Fig.4 Seismic evaluation of the main elements of the bridge
表1罕遇地震下各薄弱环节的损伤指标

Table 1 Damage indexes for the critical elements under strong earthquakes
3 抗震薄弱环节的IDA分析
本节在进行IDA分析时将每条波峰值加速度从小到大依次调成(0.1~1.0)g,调幅增量取0.1g,每条波10个分析工况。前文分析表明人工波与实际波的计算结果基本一致,因此,最终结果取10条波的平均值。
由图5(a)-(c)可知,在纵向+竖向地震激励下,随着峰值加速度PGA的增大,关键构件三个损伤状态的能力/需求单调下降,降幅在PGA较小时非常迅速,随后趋缓。相对来说,拱脚、1/4拱和2#墩抗震最不利。当PGA为0.30g时,2#右墩底截面已经出现纵筋屈服现象;在PGA达到0.4g之前,2#右墩相继进入可修复损伤和局部破坏状态。由于IDA的增量为0.1g,因此未能精确获得2#右墩分别进入可修复损伤和局部破坏损伤状态时对应的PGA。从数值上看,当PGA为0.4g时,2#右墩可修复损伤状态对应的能力/需求为0.82;局部破坏状态对应的能力/需求为0.98。由图5(d)-(f)可知,在横向+竖向地震激励下,关键构件三个损伤状态的能力/需求随着PGA的变化规律同纵桥向基本一致。其中,1#和2#墩在各种损伤状态下的能力/需求曲线最接近临界线。当PGA为0.20g时,2#右墩底首次出现纵筋屈服现象;PGA等于0.30g时,拱脚、1#和2#墩等三个关键构件的能力/需求均已低于临界值,说明构件均出现了可修复的损伤情况(在第2节中,当PGA为0.25g时,三个构件尚未出现损伤);当PGA为0.40g时,1#右墩底和2#右墩底均产生了不可修复的局部破坏机制(拱脚在PGA为0.5g之前形成局部破坏机制),表明桥梁已不适宜再承受更大的地震作用。
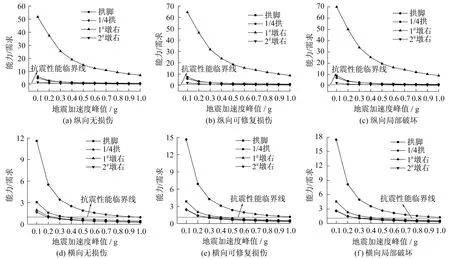
图5 关键构件损伤状态的IDA曲线Fig.5 IDA curves of damage states for the critical elements
上述分析表明,本桥在纵、横桥向的抗震富余均非常有限,当PGA达到0.2g时,该桥首次在2#固定墩处出现纵筋屈服现象;当PGA达到0.4g时,该桥率先在2#固定墩处出现局部破坏机制。上部结构中,当PGA为0.5g时,拱脚处将形成局部破坏机制。
4 结构参数对桥梁地震响应的影响
根据前期对矢跨比、拱-梁刚度比、横撑布置形式、横撑刚度等关键参数影响规律和程度的研究结果,本文限于篇幅,重点选取影响最大的两个关键结构参数,即矢跨比和拱-梁刚度比进行讨论。由于桥梁在外部属于连续梁,上部结构的变化对下部墩柱的影响较小,本节重点探讨拱圈关键截面的地震响应。
4.1 矢跨比
矢跨比是一个重要的结构参数,对拱肋和系梁的受力影响很大。梁-拱组合体系桥的拱轴线大都采用抛物线,矢跨比多在1/7~1/4之间。本文分别把拱肋的矢跨比调整为1/4、1/5、1/6、1/7,其余结构参数保持不变,探讨矢跨比的影响。
由图6(a)可知,在纵向+竖向地震激励下,当矢跨比由1/4变至1/5时,拱圈三个关键截面内力变化非常小;当矢跨比小于1/5后,各截面地震内力开始出现明显变化,其中轴力随矢跨比大幅增大,剪力随矢跨比增长相对较缓慢,而弯矩较特别,拱脚弯矩随矢跨比缓慢增大,但1/4拱和拱顶截面弯矩随矢跨比缓慢下降。从变化幅度上看,轴力增幅最大,可达95.3%;剪力和弯矩的最大增幅分别为15.0%和15.3%。
由图6(b)可知,在横向+竖向地震激励下,矢跨比对主拱圈各关键截面轴力的影响与纵桥向一致,但对剪力和弯矩的影响稍有不同。当矢跨比由1/5变至1/7时,拱圈三个关键截面的轴力最大增幅达74.4%;剪力总体呈现增大趋势,其中拱顶截面的剪力增幅最大,达57.3%;在弯矩方面,拱脚和拱顶截面均是先增后减,而1/4拱截面则不断增大,最大增幅出现在1/4拱,为15.3%。

图6 矢跨比对主拱圈关键截面地震内力的影响Fig.6 Influence of rise-span ratio on seismic interal force of key sections of main arch
4.2 拱-梁刚度比
在梁-拱组合体系中,根据拱肋与系梁相对抗弯刚度的大小可分为刚性系杆柔性拱、柔性系杆刚性拱和刚性系杆刚性拱三种类型。三种类型对拱和梁受力的分配影响很大,限于篇幅,本文仅讨论拱-梁刚度比对拱圈地震响应的影响。以本桥的原始设计参数为基准,定义拱肋和系梁的抗弯刚度之比EarchIarch/EtieItie为
(1)
分别令EarchIarch/EtieItie为0.31、0.62、1.23、2.47、4.94,研究拱圈各关键截面的地震响应变化情况。
由图7(a)可知,在纵向+竖向地震激励下,拱圈各截面内力均随拱-梁刚度比不断增大,其中弯矩增长最显著,轴力和剪力的增幅相对较缓。总体来看,当拱-梁刚度比在1.23~4.94之间变化时,各截面内力的增长曲线更陡。从数值上看,三个截面的轴力、剪力和弯矩的最大增幅分别可达10.9%、46.3%和68.7%。可见,拱-梁刚度比是影响拱圈抗震设计的重要结构参数,尤其是它对拱圈弯矩的影响比矢跨比大得多,而众所周知混凝土拱以受压为主,弯矩的增大意味着拱轴线与压力线的偏移增大,易导致拱圈开裂。在本桥所采用的拱-梁刚度比1.23下,拱圈各关键截面的地震响应处于中等水平,是相对较合理的取值。由图7(b)可知,在横向+竖向地震激励下,拱圈各截面内力亦随拱-梁刚度比不断增大,但增幅整体小于纵桥向。就数值而言,各关键截面的轴力、剪力和弯矩最大增幅分别为12.0%、19.1%和25.9%。从图中还可看到拱顶弯矩较1/4拱截面大得多,这在设计中值得引起重视。
鉴于拱-梁之间的力学平衡关系,拱-梁刚度比会大幅改变拱圈和系梁的地震内力分布,本文限于篇幅,未讨论系梁内力的变化。因此,减小拱-梁刚度比可大幅降低拱圈最不利截面的地震内力,但也可能大幅增大系梁的地震内力,在抗震设计中需要平衡。
5 结 论
本文主要结论如下:
(1) 在设计地震作用下,上部结构中的拱脚、1/4拱和下部结构的1#单向活动墩、2#固定墩是本桥抗震的薄弱环节,四者的能力/需求接近抗震临界线1.0。
(2) IDA分析表明本桥的抗震富余非常有限,当PGA达到0.2g时,2#固定墩处首次出现纵筋屈服;当PGA达到0.4g时,2#固定墩率先出现局部破坏机制;当PGA达到0.5g时,拱脚处将形成局部破坏机制。

图7 拱-梁刚度比对主拱圈关键截面地震内力的影响Fig.7 Influence of arch-beam stiffness ratio on seismic interal force of key sections of main arch
(3) 当矢跨比由1/4变至1/5时,拱圈关键截面内力变化微小;当矢跨比小于1/5后,关键截面内力变化显著。其中,轴力增幅最大,剪力和弯矩的变化相对较小。从数值上看,矢跨比对拱圈关键截面轴力、剪力和弯矩的最大影响幅度分别为95.3%、57.3%和15.3%。
(4) 随着拱-梁刚度比的不断增大,拱圈各关键截面内力不断增大,且纵桥向的增幅远大于横桥向。其中,弯矩增幅最大,轴力和剪力的增长较缓慢。从数值上看,拱-梁刚度比对拱圈关键截面轴力、剪力和弯矩的最大影响幅度分别为12.0%、46.3%和68.7%。
(5) 对于小偏压构件的混凝土拱圈来说,拱-梁刚度比对拱圈地震响应的影响更大,原因在于它对拱圈弯矩的影响远大于矢跨比,容易导致拱轴线与压力线的偏移更大,引起拱圈开裂。值得一提的是,减小拱-梁刚度比可大幅降低拱圈的地震内力,但也可能增大系梁的地震内力,在抗震设计中需要平衡。
