某超限塔楼基于IDA的地震易损性分析

张朕磊

(同济大学结构工程与防灾研究所,上海 200092)

1 工程概述

工程项目位于广西省柳州市柳东新城商务核心区域,项目总用地面积33 651.32 m2,共包括两幢高层办公塔楼、塔楼间连接裙房及其下相连的两层大地下室,总建筑面积167 489.37 m2。地上部分总建筑面积120 176.88 m2,其中A塔楼建筑面积72 032.00 m2,地上40层,建筑屋面标高165.3 m;B塔楼建筑面积29 503.88 m2,地上22层,建筑屋面标高94.650 m;裙房建筑面积18231.00 m2,地上3层,建筑屋面标高17.400 m。地下2层,建筑面积47 312.49 m2,具体详见图1。

根据建筑高度及功能特点,A、B塔楼结构采用钢筋混凝土框架-核心筒结构;裙房及地下室(塔楼外区域)采用钢筋混凝土框架结构。项目中A塔楼作为本次研究对象,由于其存在多项平面及立面不规则,根据《超限高层建筑工程抗震设防专项审查技术要点》(建质(2015)67号文印发)的规定,A塔楼属于抗震超限高层[1-2]。

图1 项目整体效果图Fig.1 Sketch of project

2 结构计算模型及抗震性能目标

A塔楼抗震设防类别为丙类(标准设防类),抗震设防烈度为6度,设计基本地震加速度为0.05g,地震分组为一组,场地类别为Ⅱ类,场地特征周期为0.35 s,结构阻比为0.05。结构体系为钢筋混凝土框架-核心筒,核心筒为第一道抗震防线,外框架为第二道防线。A塔楼屋面高度165.3 m,标准层层高4.05 m,典型平面尺寸为42 m×42 m,楼板厚度120 mm,地上共40层,地下2层。外围框架及核心筒抗震墙抗震等级均为二级。底部框架柱截面尺寸为1 400 mm×1 400 mm,核心筒外墙截面厚度为850 mm,往上依次减小。结构外圈框架梁截面尺寸为600 mm×900 mm,与核心筒相连框架梁截面尺寸为550 mm×650 mm,核心筒连梁截面高度为750 mm。A塔楼结构平面图详见图2,计算模型三维简图详见图3。

根据《建筑抗震设计规范》(GB 50011—2010)[3](以下简称《抗规》),《高层建筑混凝土结构技术规程》(JGJ 3—2010)[4](以下简称《高规》)及《超限高层建筑工程抗震设防专项审查技术要点》(建质(2015)67号文印发)的要求,对结构超限情况进行逐项对比,发现结构存在超限情况,详见表1。并根据相关规范条文选定其抗震设防性能目标为C级[5],详见表2。

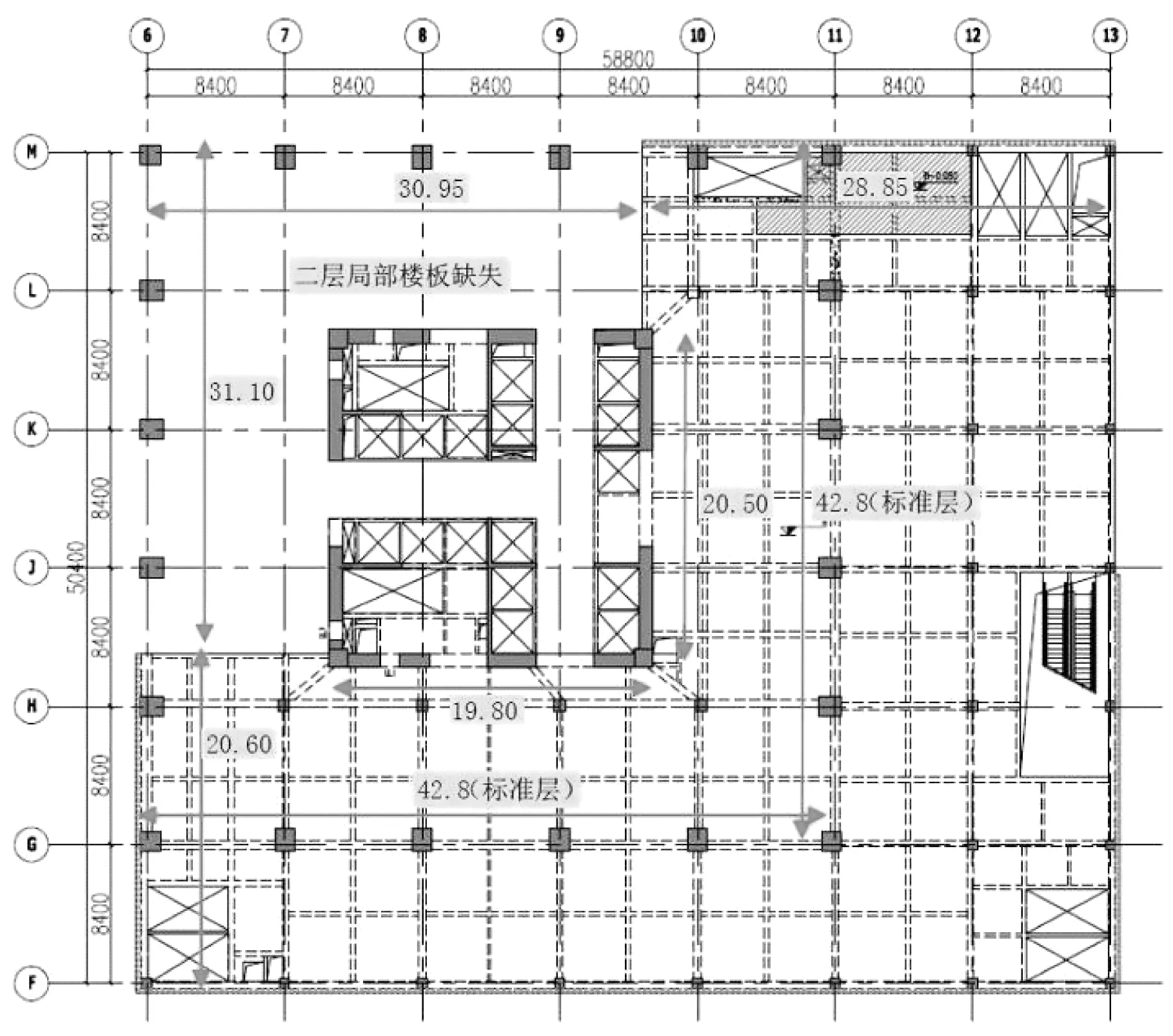
图2 结构平面图Fig.2 Structural plan

图3 计算模型三维简图Fig.3 3D structural model

表1结构超限情况

Table 1 Entry of transfinite examination

表2抗震性能设防目标

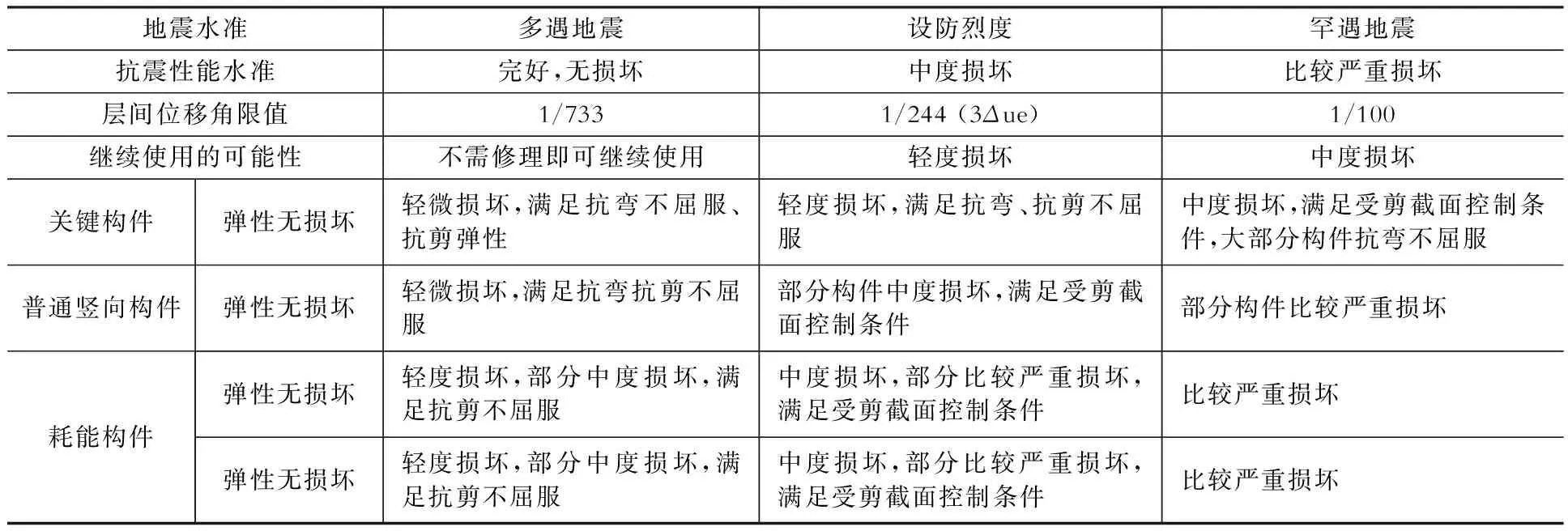
Table 2 Seismic performance objectives

针对塔楼,根据《高规》[4]及《抗规》[3]规定,设定相应构件抗震性能目标为C级。采用新版PMPMV3.1中SATWE模块,对计算模型中相关构件设定相应抗震性能等级并进行包络设计。

中震设计时相关构件性能目标:

(1) 底部加强区剪力墙正截面不屈服、斜截面弹性。

(2) 底部加强区外剪力墙、所有框架柱正截面、斜截面不屈服。

(3) 框架梁、连梁斜截面不屈服。

大震设计时相关构件性能目标:

(1) 底部加强区剪力墙正截面、斜截面不屈服。

(2) 其余剪力墙、框架柱满足抗剪截面要求。

(3) 框架梁、连梁满足抗剪截面要求。

以性能设计计算的包络配筋结果作为基础,导入后续SAUSAGE软件进行动力时程分析。

3 增量动力分析

增量动力分析方法(Incremental Dynamic Analysis,IDA)的运用是建立在动力时程分析法的基础之上,但其有别于传统的动力时程分析法。后者通过输入单条单向、双向或三向地震动记录,组合1∶0.85∶0.65的系数。可以得到结构在特定地震动持时下的响应值,但无法反映出结构在不同地震动强度下的持续反映过程。虽然Pushover可以弥补这一缺陷,但其本质仍是一种静力分析方法,不能精确反映结构的性能。然而,增量动力弹塑性分析法可以同时考虑结构抗震需求及能力的不确定性和随机性,能较合理地确定地震作用下结构的反应和破坏程度,对结构的整体抗震性能做过合理科学的评价。

3.1 基本原理

增量动力分析法[6-8]是近年来推出的一种用于评价结构抗震性能的分析方法。其基本原理是将一条特定的地震动输入记录,分别乘以一系列“比例因子λ”,从而将单条地震动记录调幅为一系列地震动记录,然后使用调幅后的地震记录分别对结构进行非线性动力时程分析,选取对应的结构性能参数作为X轴、地震强度因子作为Y轴绘制IDA曲线,并在曲线上定义相应的结构极限状态。最后,通过数据的插值和回归,分析了解曲线的趋势及离散程度,对结构的抗震性能作出评价。针对本次高层建筑研究,选取10条地震记录便能产生足够的精度以评价结构的抗震能力,并且以地震加速度峰值PGA作为地震强度因子IM,以结构层间位移角作为结构性能参数DM。具体的操作步骤可参考其他相关文献。

3.2 极限状态的定义

在得到相应的IDA曲线后,对IDA曲线进行分析,并定义相关极限状态对评估结构的抗震性能具有重要意义。早在2002年,Vamvatsikos和Cornell就已论证了IDA曲线上的三个极限状态点,即IO点、CP点、GI点。根据FEMA的相关规定,IO点为只有有限的结构损伤发生后的震后损伤状态,不需任何修补或修理即可继续使用。CP点为结构处于局部或整体坍塌边缘的损伤状态,结构可能在随后的地震中发生坍塌。GI点为结构整体坍塌。

在一条IDA曲线图表中,将曲线斜率开始发生明显较大变化的点定义为结构IO点,将曲线斜率(切线斜率)为0.2倍初始斜率的点定义为结构CP点,将曲线开始出现平缓直线(类似平台段)的点定义为结构GI点。

3.3 地震动的选取

本项目所处场地为Ⅱ类,根据《抗规》[3]中的要求,罕遇地震下场地的特征周期为0.35+0.05=0.40 s。根据上述条件,在SAUSAGE软件自带的地震波库中,寻找适合的地震波[9]。共寻找了9条天然波和1条人工波,具体详见表3所示。

该10条地震动记录与阻尼比为5%的弹性加速度反应谱对比详见图4。

表3分析所用地震动记录

Table 3 Seismic records

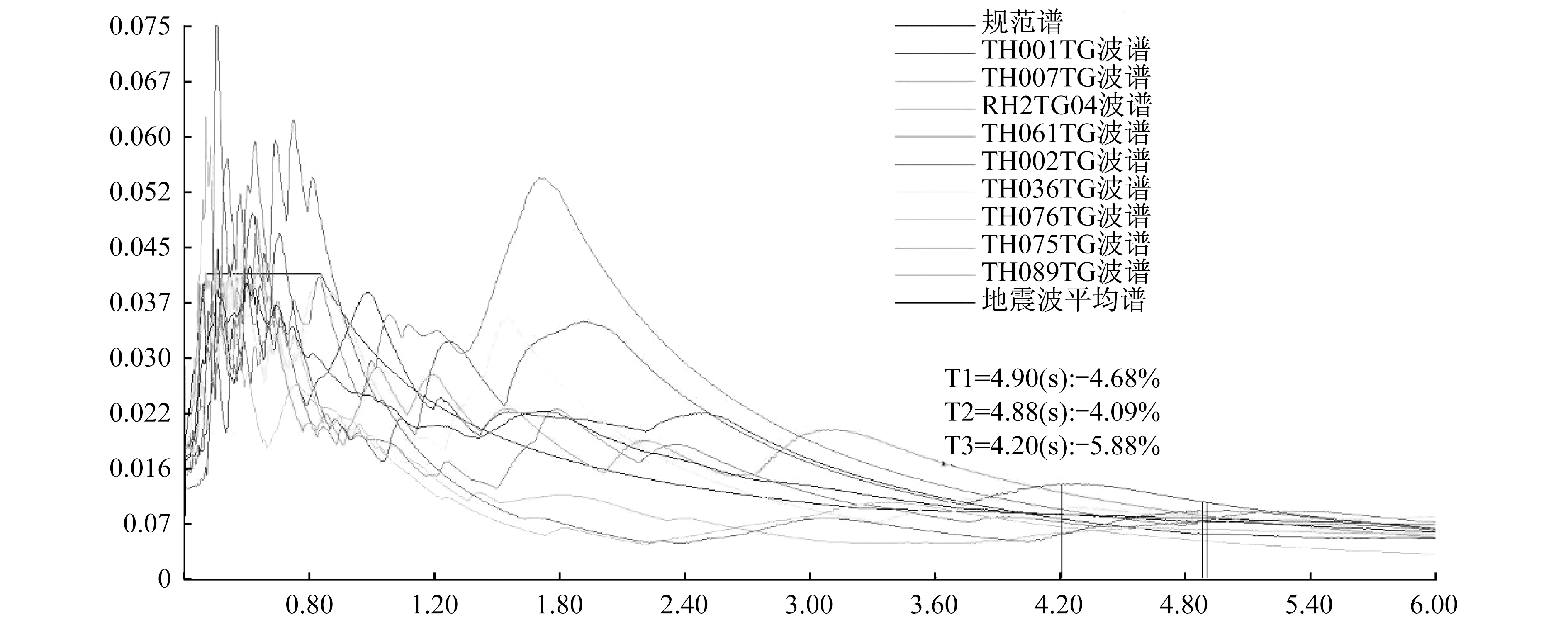
图4 地震动加速度反应谱曲线Fig.4 Seismic acceleration response spectra

从图4可知,在第一、第二平动周期点处,地震波与弹性反应谱相差不超过5%,在工程允许范围内。对地震波进行调幅时,考虑到地震动强度由小变大的初期,结构基本处于线弹性阶段,因此控制步长增量为0.1g。当地震动强度大于0.2g后,考虑到结构进入弹塑性阶段,构件强度及刚度均有不同程度的退化,因此控制步长增量为0.05g。当地震动强度大于0.5g后,由于结构整体模型的非线性属性,再次将步长增量加大为0.1g,其精度足以满足后续分析要求。对于任意一条地震波均按上述调幅原则进行13次调幅,地震峰值加速度由0.1g变化至1.0g。(0.1g,0.2g,0.25g,0.30g,0.35g,0.40g,0.45g,0.50g,0.60g,0.70g,0.80g,0.90g,1.0g)

3.4 非线性计算数值模型

采用PKPM(V3.1.5)-SAUSAGE软件对塔楼进行动力弹塑性分析。

SAUSAGE软件主要有以下几个特点:

(1) 其未作理论上的简化,直接对结构虚功原理导出的动力微分方程求解,求解结果更加准确可靠。

(2) 材料应力-应变层级的精细模型,一维构件采用非线性纤维梁单元,沿截面和长度方向分别积分。二维壳板单元采用非线性分层单元,沿平面内和厚度方向分别积分。楼板也按二维壳单元模拟。

(3) 采用Pardiso求解器进行竖向施工模拟分析,显式求解器进行大震动力弹塑性分析,计算时间大为缩短。

(4) 动力弹塑性分析中的阻尼计算创造性地提出了“拟模态阻尼计算方法”,其合理性优于通常的瑞雷阻尼形式。

在本工程的非线性地震反应分析模型中,所有对结构刚度有贡献的结构构件均按实际情况模拟。钢材的非线性材料模型采用双线性随动硬化模型,在循环过程中,无刚度退化,考虑了包辛格效应。钢材的强屈比设定为1.2,极限应力所对应的极限塑性应变为0.025。一维混凝土材料模型采用规范指定的单轴本构模型,能反映混凝土滞回、刚度退化和强度退化等特性。二维混凝土本构模型采用弹塑性损伤模型,该模型能够考虑混凝土材料拉压强度差异、刚度及强度退化以及拉压循环裂缝闭合呈现的刚度恢复等性质。当荷载从受拉变为受压时,混凝土材料的裂缝闭合,抗压刚度恢复至原有抗压刚度;当荷载从受压变为受拉时,混凝土的抗拉刚度不恢复,详见图5及图6所示。杆件非线性模型采用纤维束模型,主要用来模拟梁、柱、斜撑和桁架等构件。剪力墙、楼板采用弹塑性分层壳单元,该单元可采用弹塑性损伤模型本构关系(Plastic-Damage)、可叠加rebar-layer考虑多层分布钢筋的作用。

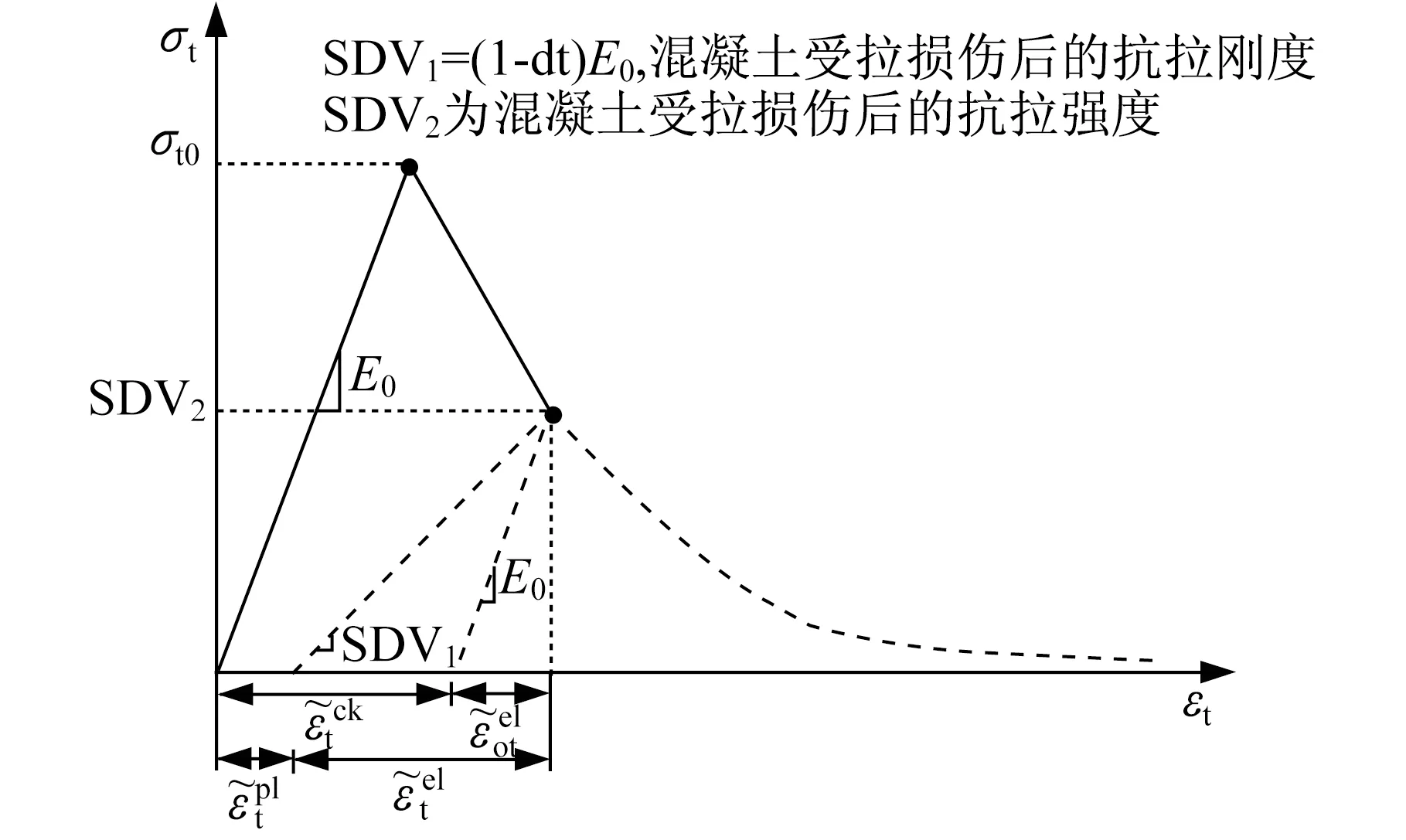
图5 混凝土受拉应力-应变曲线及损伤Fig.5 Concrete tensile stress-strain curves

图6 混凝土受压应力-应变曲线及损伤Fig.6 Concrete compressive stress-strain curves

4 IDA曲线族建立

将上述10条地震动记录依次调幅后输入SAUSAGE软件,对塔楼模型进行弹塑性分析。选取最大层间位移角为结构性能参数DM,作为横坐标X轴。选取地震峰值加速度为地震强度因子IM,作为纵坐标Y轴,建立IDA曲线族[10],并进行三阶样条插值,同时确定相应性能点位置,处理后IDA曲线族详见图7。

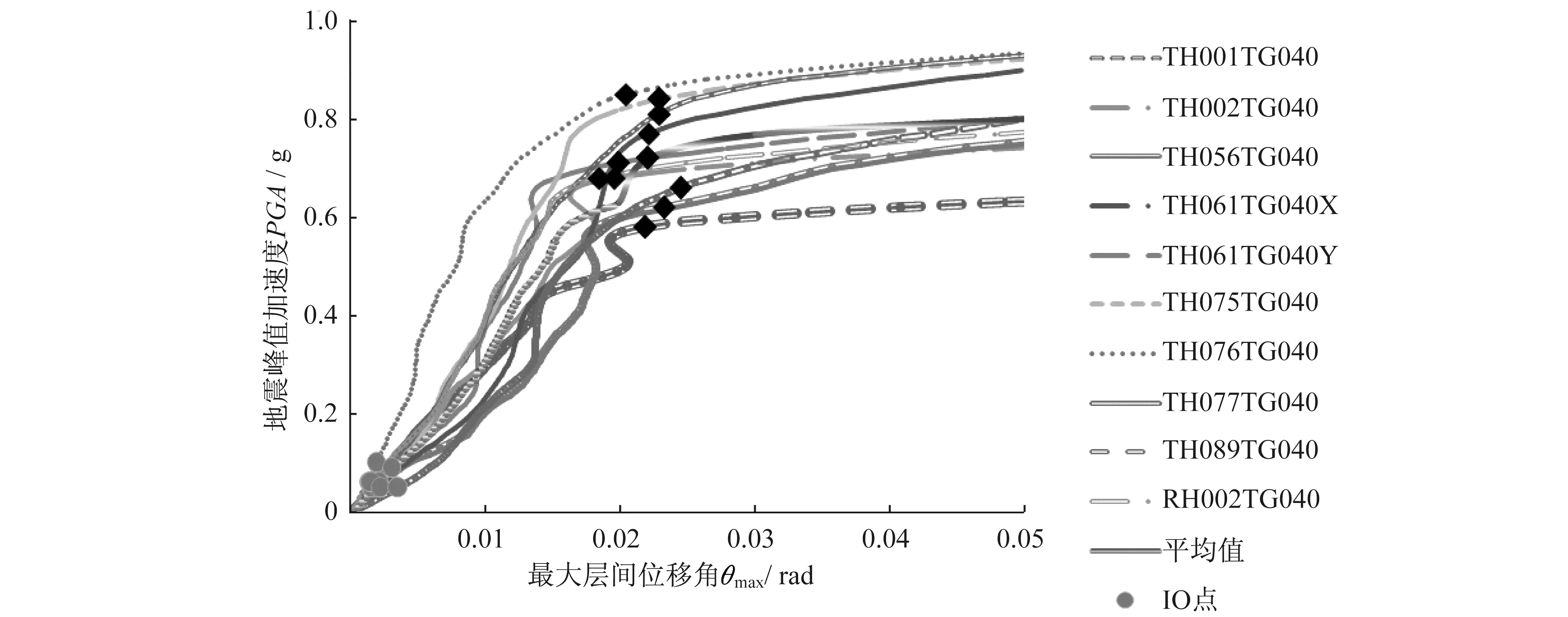
图7 IDA曲线族Fig.7 IDA curves

具体性能点详见表4。

表4地震记录极限状态点

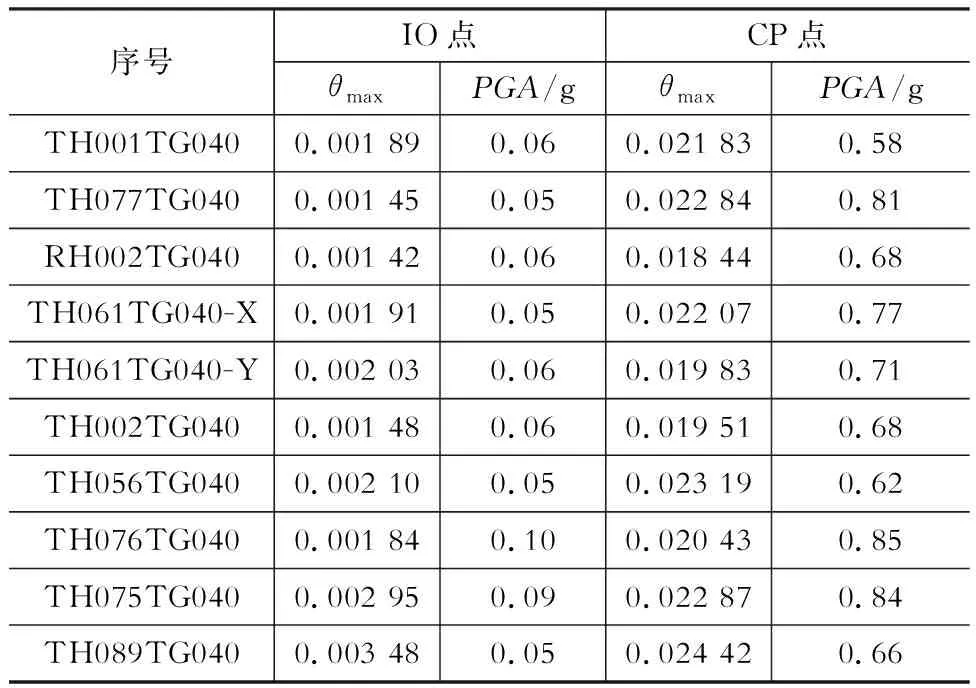
Table 4 Limit state of seismic records

5 IDA曲线分统计及分析

对IDA曲线族进行数据回归和分析,假定每条IDA曲线均服从对数分布,在某一DM值下,得到不同IM值的均值μM和不同IM对数值的标准差δM,继而得到(DM,μM),(DM,μMexp(+δM)),(DM,μMexp(-δM))三条曲线,分别为50%、84%、16%比例曲线,观察三条曲线的离散程度,对结构的抗震性能进行评估。

对图7进行百分位数统计回归,得到的16%、50%、84%分位的三条IDA曲线,详见图8,并在图中标识出每条曲线的IO、CP极限状态点,具体数据详见表5所示。

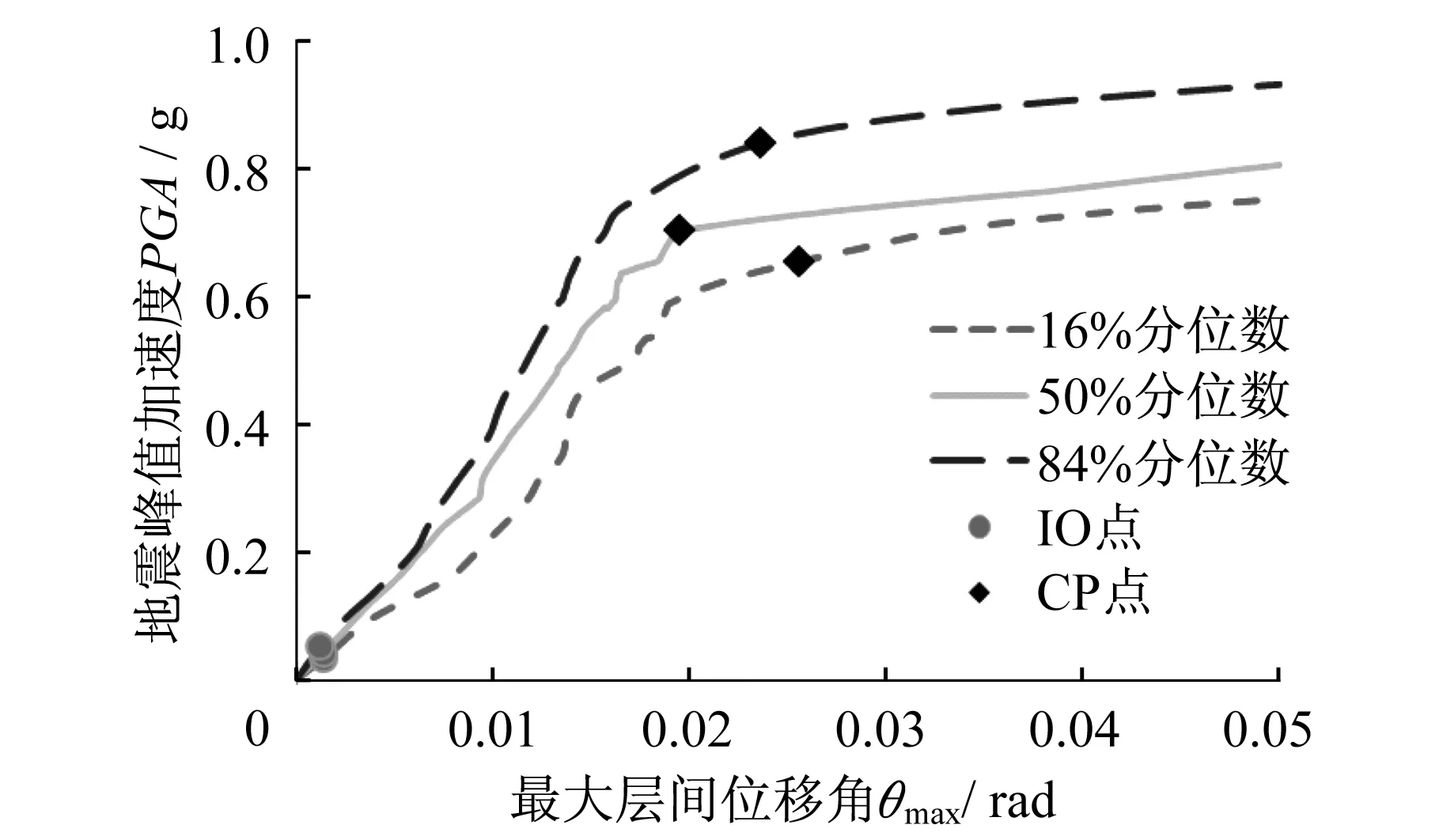
图8 统计后的16%、50%、84%分位IDA曲线Fig.8 16%、50%、84% of IDA curves

从图8可以得知,对于最上端的84%分位IDA曲线其表示的是所有分析所得的结果数据共有84%比此曲线上的数据小,这些较小的数据处于此曲线的下端。反之,共有16%的数据比曲线上的数据大,这些较大的数据处于此曲线的上端,剩余两条曲线含义同此。对于表5,以50%分为曲线上的CP点(0.0195,0.69)为例,值的是在θmax=0.0195或PVG=0.69g时,有50%的地震记录使此结构的性能状态超越了不倒塌的极限点(CP点)。通过IDA分析,可以得到结构在地震作用下所达到的性能状态,即结构的响应值。

表5统计后IDA曲线的极限状态点

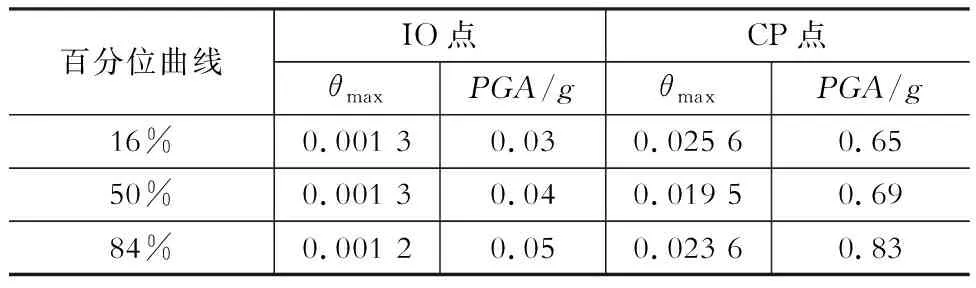
Table 5 Limit state of IDA curves

6 基于IDA的地震易损性分析

地震易损性(seismic fragility)是指在不同强度的地震作用下结构达到或超越某种极限状态的条件概率,是对建筑物所有极限状态的概率分布的描述,可以通过易损性曲线即易损性矩阵表示。

地震易损性可表示为

FR(a)=P[Ls|A=a]

(1)

式中:Ls是结构的某种性能水准或破坏等级;P[Ls]表示达到或超过该性能水准的概率,即风险的概率测度;A代表地震动的强度参数,如有效峰值加速度(PGA)、有效峰值速度(PGV)或地震烈度(MMI),本文后续计算中均以PGA作为地震动强度参数。

通过改变上述公式中地震动强度A的数值,计算结构达到或超过破坏状态Ls的地震易损性FR,然后采用统计方法进行曲线拟合,所得的光滑曲线称为“地震易损性曲线”。具体分析步骤可参考其他相关文献。

6.1 地震需求模型建立

对地震动强度IM和结构相应值DM值取对数,并进行线性回归分析。回归时以地震动强度PGA的对数作为自变量,以结构响应值θmax的对数作为因变量建立坐标系。将增量动力分析的全部计算结果统计到一张图中进行线性回归分析,具体详见图9所示,回归后公式如下:

Inθ=-3.382+1.045In(PGA)

(2)

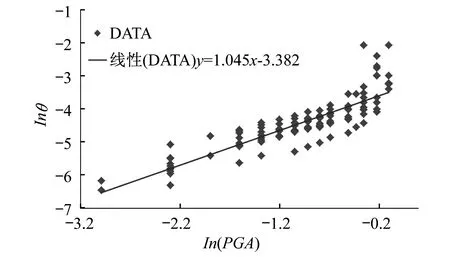
图9 回归分析Fig.9 Regression analysis

6.2 地震易损性模型建立

结构反应(C)和结构能力参数(D)的概率函数均可用对数正态分布函数表示。地震易损性曲线表示的是在不同强度地震作用下结构反应超过极限状态所对应的结构承载能力的条件概率,所以失效概率Pf可表示为

(3)

将计算结果带入上式,用PGA表示的结构在特定阶段的失效概率如下:

(4)

6.3 地震易损性曲线及易损性矩阵建立

根据图10建立该塔楼的地震易损性矩阵,详见表6和表7。

通过表6地震易损性矩阵可知,按C级抗震性能目标设计的超限塔楼在发生相当于6度小震地震时,结构仅有3.1%和2.4%的概率达到IO和完好极限状态,而超越其他几个极限状态的概率基本为0。当发生相当于6度中震地震时,结构仅有2.1%的概率达到中度损坏,发生生命安全或倒塌的概率基本为0。当发生相当于6度大震地震时,结构仅有3.2%概率达到比较严重损坏,发生倒塌的概率仍旧为0。因此,上述计算结果表明该塔楼的抗震性能较好,能满足我国抗震设计规范的三水准设防要求,且具有较多的安全富余度。

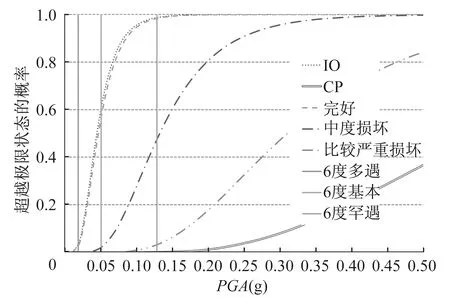
图10 地震易损性曲线Fig.10 Seismic fragility curves

表66度(0.05g)地震易损性矩阵

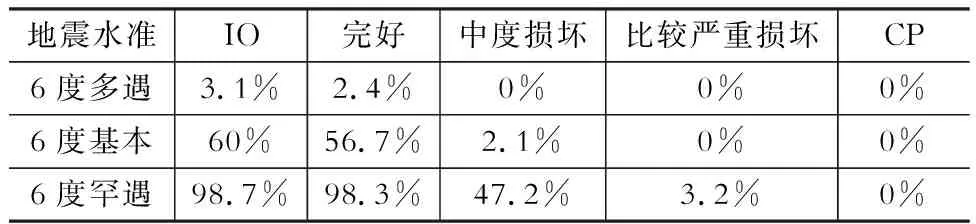
Table 6 Seismic vulnerability matrix of 6 (0.05 g)

表77度(0.1g)地震易损性矩阵

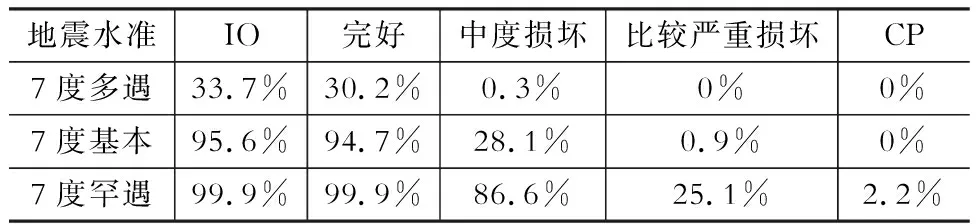
Table 7 Seismic vulnerability matrix of 7 (0.10 g)

如按设防烈度7度考虑(计算结果详见表7),该塔楼在遭遇小震地震时,仍具有一定的安全储备,在遭遇7度中震地震时,能较好的控制构件的破坏程度。在遭遇7度大震地震时,塔楼倒塌的失效概率也仅为2.2%。

7 结语

通过对广西柳州某超限高层塔楼进行了单向水平地震作用下的IDA分析,得到多条地震记录下的结构反应IDA曲线和结构性能点,统计出16%、50%、84%比例的IDA曲线。同时结合地震易损性理论,明确了基于IDA的地震易损性分析的步骤、计算结构在各指定水准下超越极限状态的概率、建立该塔楼的地震易损性曲线和地震易损性矩阵。

分析结果表明按C级抗震性能目标设计的塔楼具有较好的抗震性能,且具有较多的安全富裕度,该塔楼能满足我国抗震设计规范的三水准设防要求。

同时,通过实际工程算例,初步建立增量动力法和地震易损性分析的计算流程和分析步骤,为日后其余工程超限分析中大震弹塑性分析的完善打下了良好的基础。通过地震易损性曲线和易损性矩阵,可以直观、科学地得知结构失效的概率,从以往大震分析主要为定性分析转变为定量分析迈进一大步。