钢板-高强混凝土组合剪力墙火灾反应数值模拟

2018-07-14肖建庄卫凯华董毓利

结构工程师 2018年3期

肖建庄卫凯华柳献董毓利

(1.同济大学建筑工程系,上海 200092; 2.同济大学地下建筑与工程系,上海 200092; 3.华侨大学土木工程学院,厦门 361021)

0 引言

钢板-混凝土组合剪力墙兼有钢结构和混凝土结构的优势,具有承载力高、延性好、刚度大等优点,在高层结构中应用日趋广泛,将高强混凝土与钢板剪力墙结构相结合,更是能够有效减小构件截面,增大建筑空间。对于钢板-混凝土组合剪力墙的力学性能,国内外已经有较多研究[1-3]。

近年来,李国强等[4]对钢结构抗火性能进行了深入研究。同时肖建庄[5]对高强混凝土结构抗火性能进行了研究,韩林海和宋天诣[6]对于钢-混凝土组合柱、组合梁耐火性能都进行了深入的理论及试验研究。

目前,关于钢板-高强混凝土组合剪力墙的抗火研究相对较少。本文主要研究墙体厚度、钢板厚度及墙体约束条件对钢板-高强混凝土组合剪力墙火灾反应的影响,主要包括温度场以及墙体变形情况。研究结果可以为组合剪力墙的抗火设计提供理论依据,同时也为有关规范的进一步完善提供参考。

1 数值模拟

1.1 研究对象

为了与已有的模型试验进行校验,选取肖建庄等[7]完成的试验进行有限元模拟。

该试验以4榀剪力墙试件为研究载体,进行剪力墙的单面受火试验,采集炉膛温度、剪力墙混凝土内部温度、平面外挠度等信息,获取剪力墙的温度场和变形情况以探究钢板-高强混凝土组合剪力墙的火灾反应。

试验中各试件的配钢率相同,但构造类型方面有所区别,分别为高强混凝土剪力墙、整体钢板-高强混凝土组合剪力墙、分段钢板-高强混凝土组合剪力墙和型钢-高强混凝土组合剪力墙。试验过程中,剪力墙直立贴于试验炉口,单面受火,其侧边用耐火砖以及耐火石棉封砌。火灾时墙体的背火面与空气的传热以对流形式进行,而侧面可视为绝热边界条件。墙体的受火面和炉膛的热量交换主要以对流和辐射的形式进行。升温曲线为ISO834标准升温曲线,曝火时间为120 min,试验按建筑构件耐火试验方法[8]进行。

由于试验周期较长,研究的参数也有限,利用有限元数值模拟,则能够研究更多的参数,因此选取该试验中的钢板-高强混凝土组合剪力墙试件FW (Fire Wall)进行数值模拟,其截面形式如图1所示,墙体高度为1 000 mm。在对该墙体进行模拟并利用试验校验后,将进行更多的变参数分析。

1.2 分析假设

火灾作用下,剪力墙温度场是非线性变化,且影响温度场的因素繁多。为了简化计算,减少分析的难度,因此采用以下几点假定[9-13]:

(1) 温度场沿剪力墙的高度方向不变,其内部温度场问题属于二维问题;

(2) 剪力墙内应力场对温度场的影响忽略不计;

(3) 混凝土是均匀的各向同性材料;

(4) 混凝土内部无热源,不考虑材料内部的反应热,同时也不考虑墙体内水分蒸发和迁移对温度场的影响。

图1 FW截面形式Fig.1 Sectional view of FW

1.3 模型建立

剪力墙的温度场计算是通过对构件表面的环境温度、混凝土的热工性能以及边界条件的量化,模拟结构内部各处的温度变化,以下采用ANSYS通用有限元软件进行模拟[14-15]。有限元模型如图2所示,分别为混凝土、钢板及钢筋骨架。

图2 有限元模型Fig.2 Finite element model

温度场分析时,混凝土采用SOLID70单元[16-17]模拟。钢板采用SHELL57单元,在迎火面处的SOLID70单元表面覆盖一层SURF152单元,用于热辐射分析。

在挠度分析时,将热分析单元转化为力学分析单元。其中,将SOLID70单元转化为SOLID65单元,将SHELL57单元转化为SHELL43单元,将LINK33单元转化为LINK8单元。在剪力墙底部增加25 mm厚的垫块,垫块底部的约束条件为固端约束,并导入计算得的温度场,从而计算出不同时刻试件的变形。

1) 热工参数

在进行有限元软件分析前,需要确定材料的热工参数,采用不同材料热工模型,计算出火灾下混凝土构件内部的温度场结果有所不同。模拟中采用的热工参数见表1。

表1有限元模型所采用的热工参数

Table 1 Thermal parameter adopted in the finite element model

边界条件中的各参数选取如下数值[18]:墙体表面和空气的对流换热系数h取决于空气的流动速度,其数值一般在20～80 W/(m2·K)之间。从点火开始到300 min时,炉膛内的鼓风机均处于开启状态,因此迎火面的空气流动速度较快,取h=40 W/(m2·K)。背火面的空气流动速度较慢,取h=20 (W/m2·K)。初始时墙体内部温度和环境温度基本一致,根据炉温热电偶初始时的读数取为20 ℃。熄火后,由于背火面混凝土温度较高,背火面附近的空气温度略高于室温,取为50 ℃。形状系数取φ=1.0,迎火面的综合辐射系数取hr=0.5。

升温曲线采用试验实测升温曲线。采用荷载步文件进行加载,由于升温过程温度变化大,因此荷载步逐渐变长,前两个荷载步长度为5 min,从10 min到120 min每个荷载步为10 min,从120 min到180 min之间的荷载步为15 min,后180 min每个荷载步为30 min,共23个荷载步。

2) 力学参数

混凝土高温下的力学性能参数采用了胡海涛和董毓利的研究成果[23],高温下高强混凝土的棱柱体抗压强度为

(20 ℃≤T≤1000 ℃)

(1)

式中:fc表示高强混凝土常温时的抗压强度设计值;fcT表示高强混凝土高温时的抗压强度设计值。

高温下高强混凝土的峰值应变可表示为

(20 ℃≤T≤800 ℃)

(2)

高温下高强混凝土的应力应变关系可采用指数函数方程式表示如下:

y=xe(1-x2)/2

(3)

(4)

式中:σ和ε分别表示高强混凝土的应力和应变。ε0T为高温下的高强混凝土的峰值应变;ε0为常温下的高强混凝土峰值应变。

假设钢材高温下的应力-应变关系为二折线模型,钢材在屈服后应力保持不变。钢材高温下的屈服强度和弹性模量采用吕彤光等[22]提出的计算式:

(20 ℃≤T≤900 ℃)

(5)

(20 ℃≤T≤900 ℃)

(6)

式中:fyT为高温下的钢材屈服强度;fy为常温下的钢材屈服强度;EsT为高温下的钢材的弹性模量;Es为常温下的钢材弹性模量。

1.4 试验验证

经有限元模拟发现,加热120 min后,FW剪力墙中部截面温度场分布如图3所示,截面温度最大的地方位于剪力墙端部的角点处。单面受火的剪力墙,温度场呈层状分布,由于混凝土的热惰性,距离迎火面越近,温度梯度越大。钢板的导热系数远远大于混凝土的导热系数,钢板两端型钢周围处的混凝土的等温线发生了突变。

图3 FW熄火时刻横截面的温度场分布Fig.3 Temperature field of FW at flameout moment

为了下文分析和简化表达,下文图中所指路径一为距离剪力墙底部0.5 m处截面中部;路径二为距离剪力墙底部0.5 m处截面端部有钢板处。

图4为FW的迎火面、背火面及中间点在有限元模拟和试验中的温度变化曲线。迎火面为距离迎火面5 mm处的测点,背火面为距离背火面5 mm处的测点,中间点为剪力墙厚度方向中点。剪力墙沿截面的温度场为瞬态温度场,试验和有限元分析中的结果非常接近。试验所测的迎火面最高温度比计算值高,这可能是由于混凝土材料的离散性和施工预埋过程中的偏差以及试验中存在的混凝土爆裂,导致迎火面一侧的热电偶直接暴露于火场中,或测量误差。在升温阶段,剪力墙的截面中部和背火面的温度上升略快于有限元模型,可能是因为试验时的爆裂导致中间点和背火面与迎火面的距离减小,也可能是由于试验过程中存在的误差。

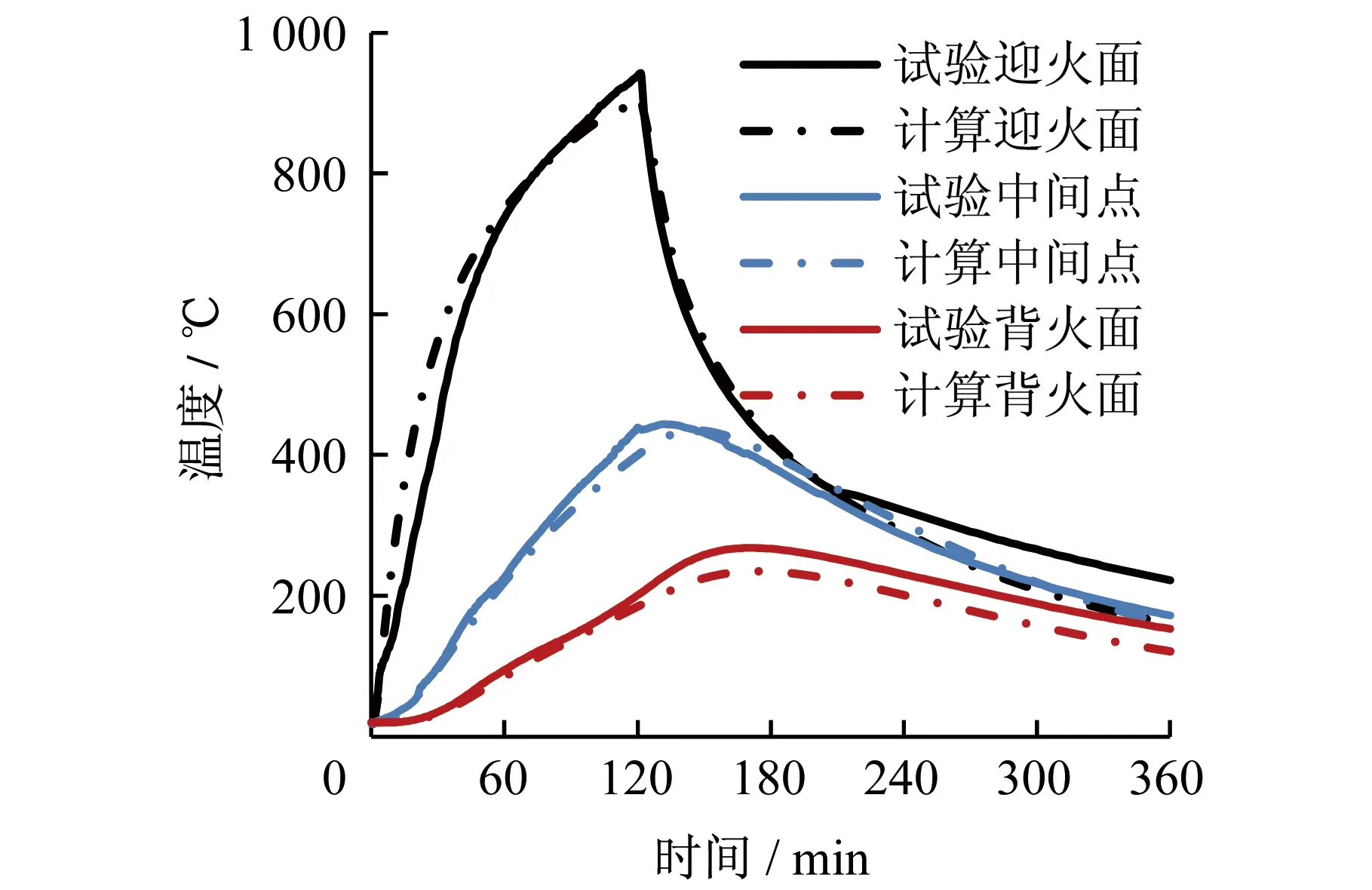
图4 FW温度场数值分析与试验对比Fig.4 Comparison of temperature variation from FEM and experiment

图5和图6为FW截面沿路径一和路径二的温度分布,60 min,120 min,240 min,360 min四个时刻均是在升降温过程中从点火开始计算。图5中温度曲线平滑,而图6中因为端部钢板存在的缘故,导致钢板与混凝土交接点处出现了突变,并且在距离迎火面80 mm至120 mm区间温度梯度变化较为平缓。但随时间增加,整体温度梯度逐渐减小,到360 min时,温度分布已经趋近于均匀,钢板与混凝土交接点处的突变已经不再明显。

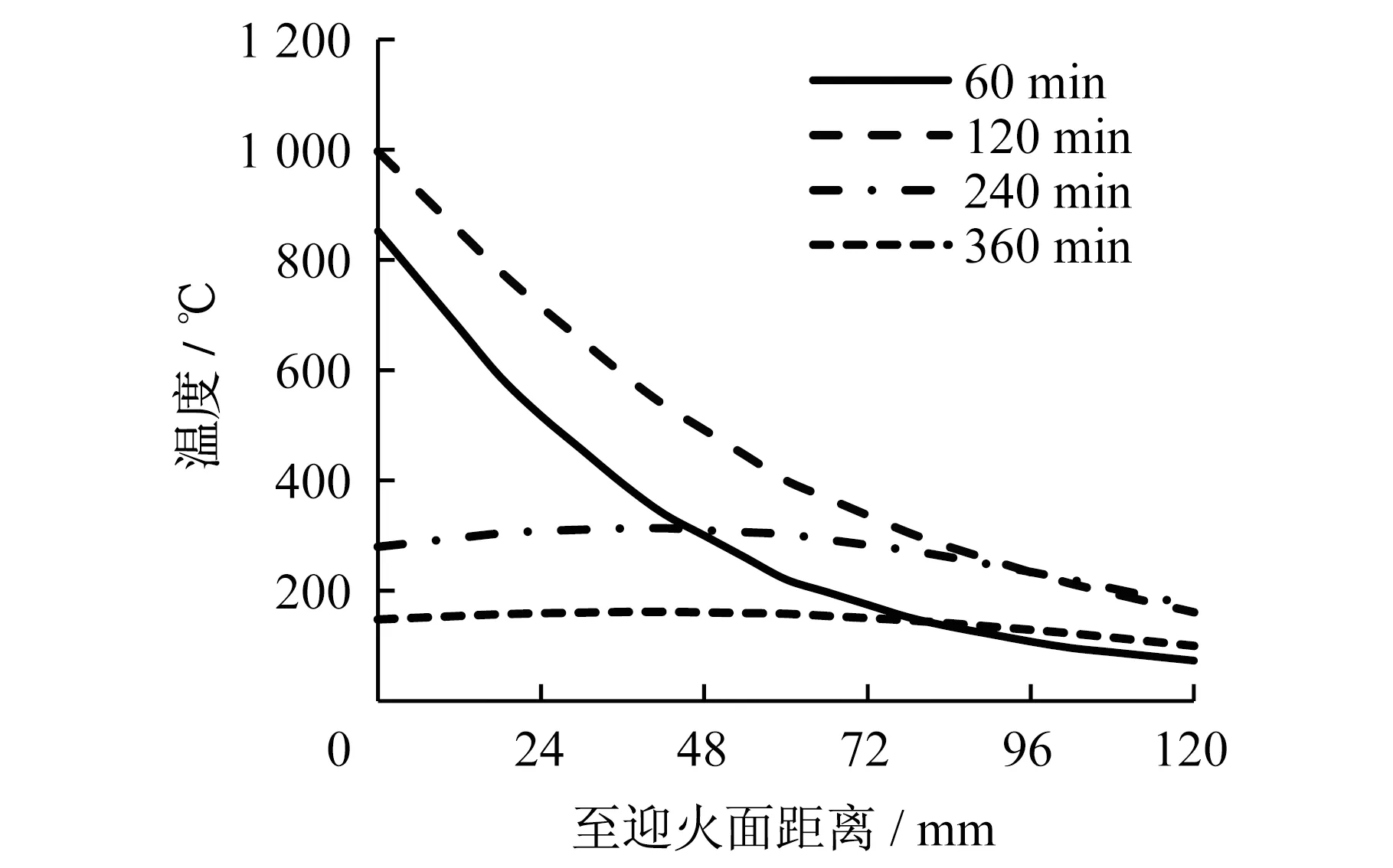
图5 FW路径一处各时刻温度分布Fig.5 Temperature distribution on route 1 of FW

图6 FW路径二处各时刻温度分布Fig.6 Temperature distribution on route 2 of FW

在熄火时刻,有限元中FW墙身和钢板的挠度分布云图如图7所示,同一截面处,距离两端越近,该点的位移越大。FW在受火过程中,位移最大的位置在剪力墙顶部的端部处。

图8为升降温过程中,剪力墙顶部位移在试验和有限元模拟中随时间变化的对比。无论是在升温阶段还是在降温阶段,测点位移的试验值始终略大于计算值。可能由于在试验升温过程中,迎火面发生爆裂,墙身部分混凝土脱落,导致墙体刚度下降,或试验过程中存在误差。在熄火时刻(即加热120 min后),测点位移的试验值为23.7 mm,计算值为22.7 mm。在熄火后180 min时,测点的残余位移的试验值为1.89 mm,计算值为0.97 mm。

图7 FW熄火时刻混凝土墙身及钢板平面外挠度Fig.7 Deflection of concrete and steel of FW at flameout moment

图8 FW顶点位移-时间曲线Fig.8 Displacement-Time curve on top of FW

对比可以发现,建立的有限元模型,能够模拟钢板-高强混凝土组合剪力墙的真实火灾反应,在此基础上,将对钢板-高强混凝土剪力墙进行变参数分析。

2 变参数分析

为了对钢板-高强混凝土组合剪力墙的火灾反应进行进一步的研究,利用经过试验验证的仿真模型继续针对墙身厚度、钢板厚度及约束条件三个参数展开了探讨。

表2给出了各剪力墙的代号和结构参数,其中WT代表Wall thickness(墙体厚度),ST代表Steel plate thickness(钢板厚度),WC代表Wall constraints(墙体约束)。这9榀剪力墙中,为方便表达,WT120、ST3、WC1与FW完全相同,其余6榀剪力墙除了墙身厚度、钢板厚度和约束条件与FW不同外,其他的材料、配筋和尺寸等参数均与FW相同。其中ST0试件,钢板厚度为0,即为普通钢筋混凝土剪力墙。

表2钢板-高强混凝土剪力墙参数

Table 2 Steel plate-HSC shear wall parameters

2.1 墙体厚度

图9和图10分别为WT160和WT200熄火时刻横截面的温度场。可以看到,由于WT160端柱处两相邻面受火,故其角点温度最高,为1 036.5 ℃,而WT200墙体只有单面受火,因此WT200迎火面经历的最高温度997.7 ℃,低于WT160墙体。

表3为WT120、WT160和WT200截面中部迎火面和背火面各时刻的温度对比:在升温阶段,三种墙身厚度的剪力墙迎火面温度很接近,在降温2 h后,三榀剪力墙迎火面的温度变化略有不同,墙身厚度越厚,其迎火面温度下降的越慢;如图11所示,墙身厚度越大,背火面升温的速度越慢,背火面达到最高温度所需的时间也越长,并且所能达到的最高温度的值越小,如表4所示。

图9 WT160熄火时刻横截面温度场分布Fig.9 Sectional temperature distribution view of WT160 at flameout moment

图10 WT200熄火时刻横截面温度场分布Fig.10 Sectional temperature distribution view of WT200 at flameout moment

表3不同墙身厚度的剪力墙截面中部迎火面和背火面各时刻的温度

Table 3 Central temperature of exposed and unexposed side of shear walls with different widths

图11 不同墙厚剪力墙背火面温度变化Fig.11 Temperature variation of unexposed side with different widths

图12是三种墙身厚度剪力墙顶点的位移随时间变化情况,图13和图14分别为WT160和WT200在不同时刻的挠度。在升降温过程中,墙身厚度越厚,墙体刚度越大,剪力墙变形速度越慢,顶点位移值越小;厚度为160 mm和200 mm的剪力墙,顶点位移的最大值分别为16.7 mm和12.2 mm。

表4不同墙身厚度剪力墙背火面
最高温度及其对应时刻

Table 4 The moment of the highest temperature of shear walls with different widths

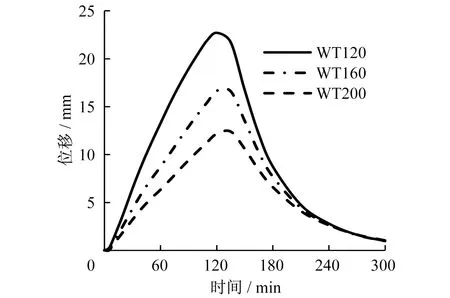
图12 不同墙厚剪力墙顶点位移变化Fig.12 Top displacement at top of walls with different widths

图13 WT160不同时刻挠度Fig.13 Deflection of WT160 at different moments

图14 WT200不同时刻挠度Fig.14 Deflections of WT200 at different moments

2.2 钢板厚度

钢板的厚度对于剪力墙的温度场和挠度变形有一定的影响,需要对不同钢板厚度的剪力墙火灾过程中的温度场和变形情况进行分析。

2.3 墙体约束条件

在试验中,剪力墙底端为固定约束,而在实际建筑火灾中,剪力墙的约束条件是上下两端皆有约束。由于假定温度沿高度不变,温度场为二维问题,因此WC1与WC2的温度场相同。

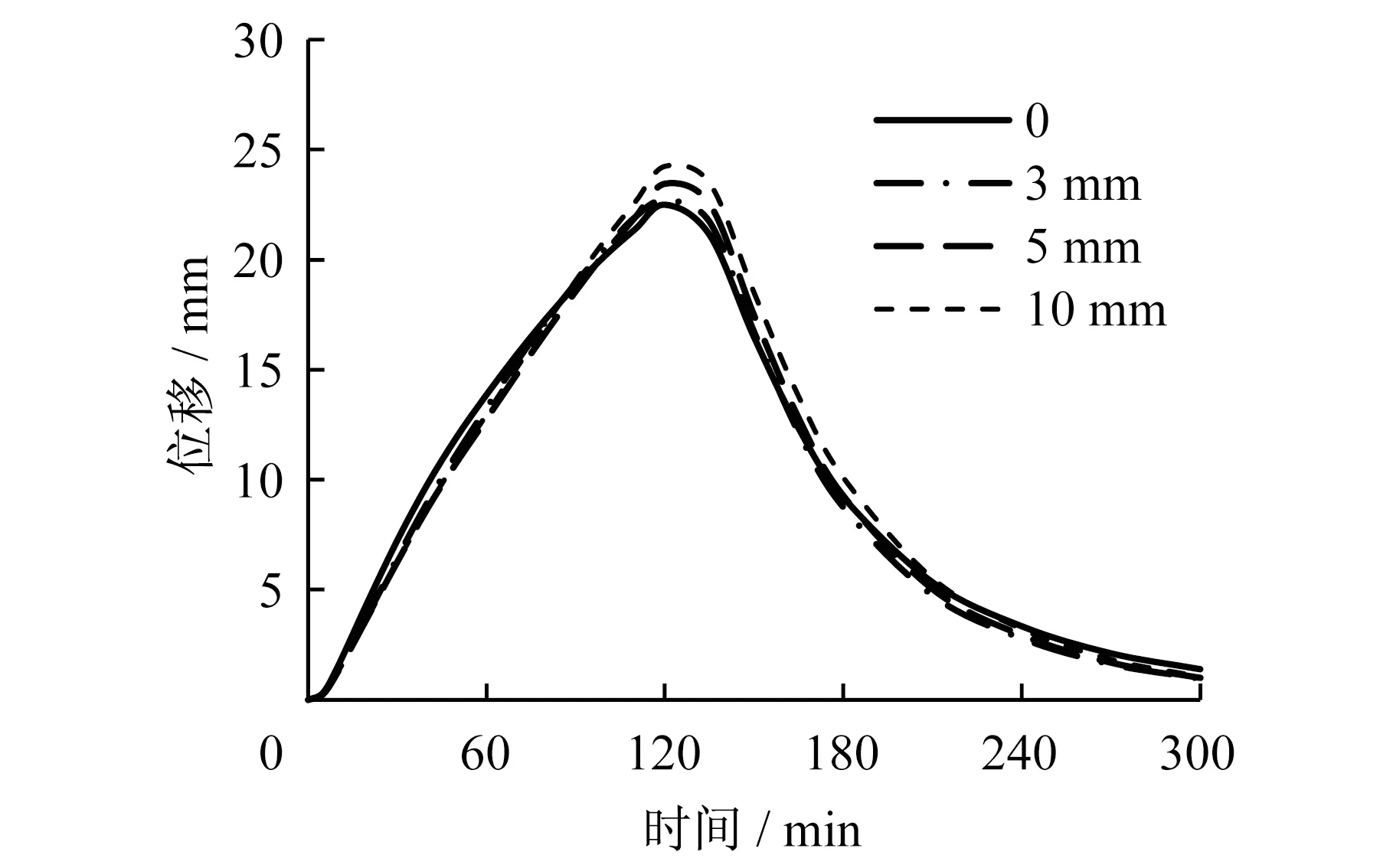
图15 不同钢板厚度剪力墙顶点位移-时间曲线Fig.15 Displacement-time curves on top of wallswith different steel plate thickness

图16为两端约束的剪力墙在加热120 min后熄火时墙身和钢板的平面外挠度。图17和图18分别为WC1和WC2不同时刻的挠度图。可以看到一端固定的WC1,其挠度变形朝向背火面,而两端固定的WC2的变形则朝向迎火面。表5为WC1及WC2不同时间的顶部及墙体中部位移,WC1在距离墙底0.5 m处经历的平面外位移最大绝对值为4.21 mm,远大于WC2同一位置经历的平面外位移最大绝对值1.32 mm。所以,约束类型对于升降温过程中剪力墙的变形影响明显,相同试件两端均固定约束的情况下,平面外的变形远小于一端固定约束的情况。