300 MW循环流化床锅炉气固流动特性的CPFD模拟*
2018-07-14曾胜庭马琎晨赵海波
曾胜庭,陈 曦,马琎晨,赵海波†
(1. 广东粤电集团云河发电有限公司,广东 云浮 527328;2. 华中科技大学煤燃烧国家重点实验室,武汉 430074)
0 前 言
循环流化床锅炉中气固两相在炉床内充分接触,传热及传质效果好,具有燃烧效率高、适合低品质燃料、负荷调节范围宽、低污染物排放等特点[1-2],广泛应用于燃煤发电、生物质和固体废弃物处理等领域。
对于循环流化床锅炉的运行,国内外大量学者利用冷模和热态实验对其气固流体动力学特性进行了系统的研究[3-4];同时基于工业锅炉的实际运行测试也有相应的进展[5-6]。但实验研究在实验台尺寸和运行条件方面同实际锅炉存在一定的差异,因此所获得的结论通常不能直接应用于工业生产;工业测试的整个过程虽然是基于锅炉的真实运行状态,但由于存在测试难度、测试条件的限制,也通常不能获得炉内详细气固两相流的传热传质情况。因此,随着计算流体力学(computational fluid dynamics, CFD)和计算机硬件的发展,数值模拟因其模拟了炉膛内的环境,能够较为准确地描述炉膛内的气固流体动力学特性和燃烧传热情况,同时能够得到实验和实际运行过程中不易测量的参数,因而成为研究循环流化床锅炉的一种有效手段。XIE等[7-8]采用MP-PIC方法模拟了燃烧垃圾的75 t/h循环流化床锅炉,模拟考虑了垃圾燃烧过程中的污染物释放以及反应过程,系统分析了循环流化床锅炉在运行过程中的气固流动特性、气体浓度分布、压力分布、温度分布等关键信息,同时对循环流化床锅炉在运行过程中的壁面磨损情况也进行了研究。张彦军等[9]对 600 MW 超临界循环流化床锅炉进行整体模拟,研究了二次风的穿透特性以及旋风分离器不均匀性等问题。许霖杰等[10]对1 000 MW超临界循环流化床锅炉环形炉膛气固流场进行了模拟,分析了炉膛中不同位置的颗粒浓度分布以及各旋风分离器入口的质量流量不均匀性。王超等[11]对 600 MW 超临界裤衩腿六分离器循环流化床锅炉炉膛的气固流场进行数值模拟研究,分析了炉膛内的颗粒浓度和颗粒速度分布,比较了六分离器的气固流量。
但CFD方法计算效率偏低,且在计算高固相浓度的气固两相流方面存在一些不足。经过不断探索,研究者们发展了一种CFD的分支——计算颗粒流体力学(computational particle fluid dynamics,CPFD)。SNIDER等[12-14]结合双流体模型和计算流体力学–离散元方法(CFD-DEM)模型,对计算过程做了较大程度的简化,采用欧拉–拉格朗日方法来处理流动过程中的流体相和颗粒相,从而最先实现了气固两相颗粒粒子系统的快速CPFD模拟。CPFD已被应用于大型流化床气固流动的数值计算,并且取得了很好的计算结果。WANG等[15-16]对一个循环流化床冷态实验台进行了 CPFD建模和计算,发现床料密相堆积体积分数对回料阀中的颗粒流动会产生很大影响;之后,他们用优化后的参数进行模拟,研究了不同工况下物料循环的状态,计算结果同实验结果吻合较好。邱桂芝等[17]采用 CPFD数值模拟方法研究了循环流化床环形炉膛冷态实验台内的气固流动特性,模拟得到的炉膛内轴向压力分布和返料流率均与实验结果吻合较好,同时还分析了炉膛出口气固流动不均匀性。张瑞卿等[18]模拟了Chatham锅炉的热态运行,得到了从启动到稳定运行的气固流动和燃烧动态结果,并根据模拟结果准确预测出了炉内壁面磨损的发生位置。
对于循环流化床锅炉的模拟,目前已有的工作大都选择忽略旋风分离器和回料阀,而重点对炉膛进行针对性的研究。本文采用CPFD方法,对实际运行工况下的300 MW循环流化床锅炉全床进行模拟,以欧拉–拉格朗日方法来处理气固流动中的流体相和颗粒相,以研究循环流化床锅炉整体的气固流动特性和细节,包括固相颗粒浓度和速度在炉膛内的分布、固体循环流量、系统压力平衡以及回料阀的运行情况等锅炉运行状态,以指导实际工况下的运行。
1 模拟对象
本文中的模拟对象为广州粤电云河发电有限公司300 MW循环流化床锅炉,是由上海锅炉厂有限公司生产制造的SG-1036/17.5-M4506型亚临界参数中间再热循环流化床锅炉。模拟过程中采用的锅炉模型如图1和图2所示,按照模型尺寸与实际尺寸1∶1绘制,炉膛高40 m、宽28 m、厚8.9 m。整个循环流化床锅炉模型由锅炉炉体、旋风分离器、回料阀组成,其中三个旋风分离器均为单侧布置。为了使对炉膛内的气固流动模拟更加准确,根据实际情况布置二次风管。锅炉内部床料粒度分布如图 3所示,平均粒径为 231.25 μm,采用激光粒度仪(Malvern,Master Min)测试;真密度为2 895.47 kg/m3(真密度仪,Micromeritics,AccuPyc1330)。模拟过程中循环流化床锅炉整体温度为1 163 K,壁面为绝热边界条件,模拟过程中具体的参数设置如表1所示。初始时流化床内压力为1个大气压,旋风分离器出口设置为压力出口,表压为0 Pa。床料装填于炉膛底部,密相体积分数0.47,填料高度1.1 m。模拟采用的网格数目为1.4 × 106,时间步长0.000 1 s,模型网格采用六面体网格,同时对炉膛底部锥形区和回料阀部分进行局部加密,如图2所示。气固曳力模型采用Gidaspow模型,颗粒法向恢复系数0.89,切向恢复系数0.68[19-20],采用GPU并行计算。
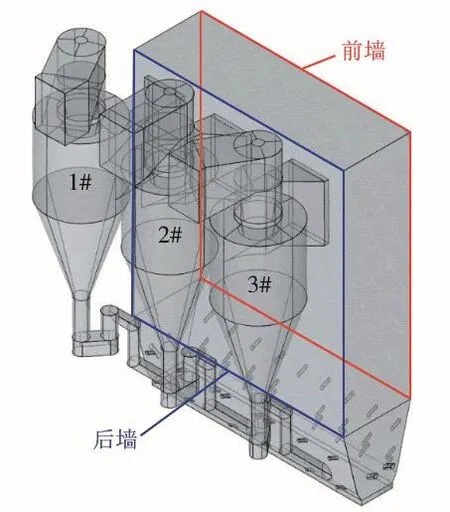
图1 循环流化床锅炉模型Fig. 1 Physical model of the CFB
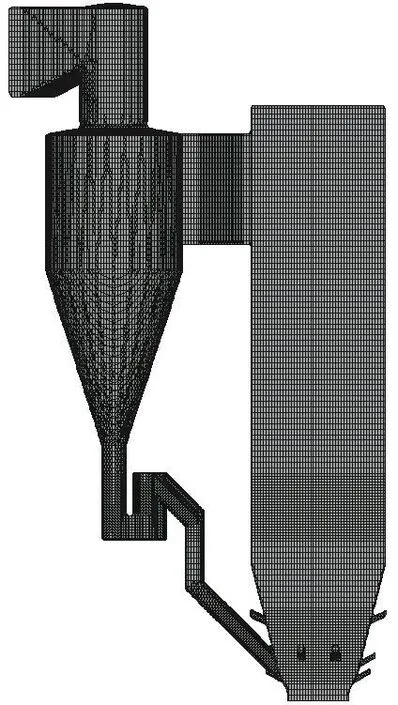
图2 模拟过程中采用的网格Fig. 2 Mesh configuration of the CFB
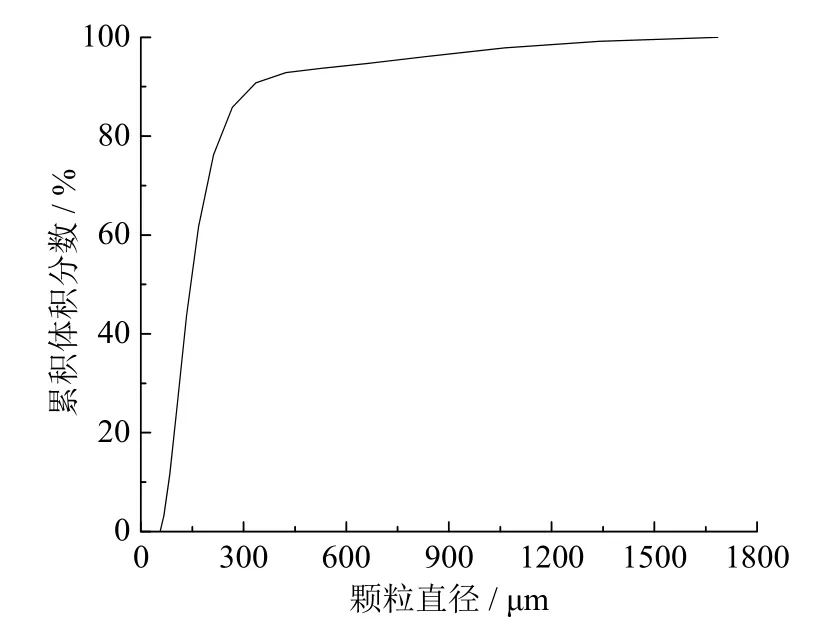
图3 床料粒度分布Fig. 3 Size distribution of bed material
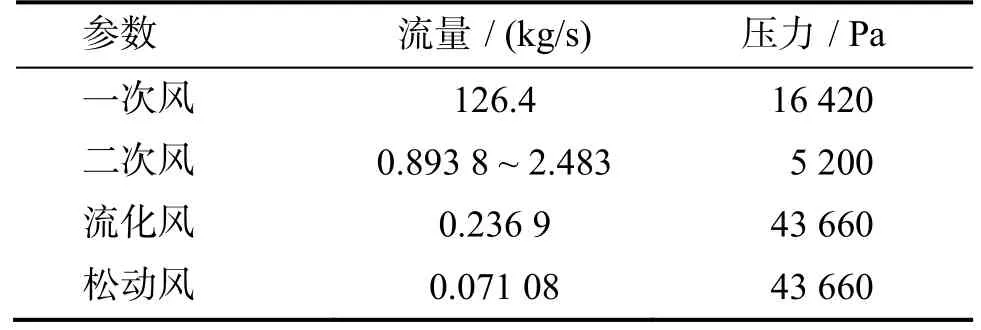
表1 基本参数Table 1 Basic parameters
为确定模拟过程中达到稳定状态的时间,统计了通过炉膛中高度8 m和28 m两个位置截面的累积床料量,如图4所示,图中曲线的斜率即为通过该截面的固体循环流量。在t= 28.2 s之后两条曲线接近于平行,这表明炉膛内物料的固体循环流量达到一致,认为循环流化床的运行达到了稳定状态。因此,下文中关于稳定状态下运行参数的分析,则取t= 28.2 s之后不同时刻的流场样本进行时均处理(28.2~40 s)的结果。
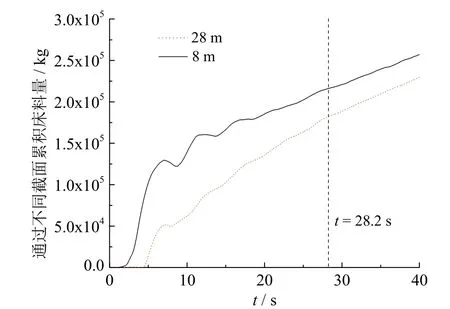
图4 通过炉膛中截面的累积床料量Fig. 4 The cumulative bed material through the furnace central section
2 控制方程
2.1 气固两相流模型
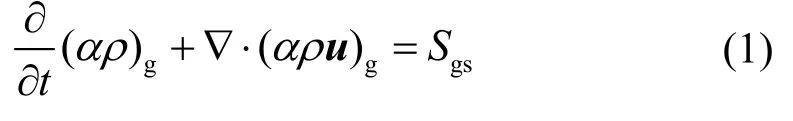
其中,下标g、s分别代表气相(连续相)和颗粒相;α、ρ和u分别为气相的体积分数、密度和瞬时速度矢量;Sgs为质量源项。
2.2 连续相动量守恒方程
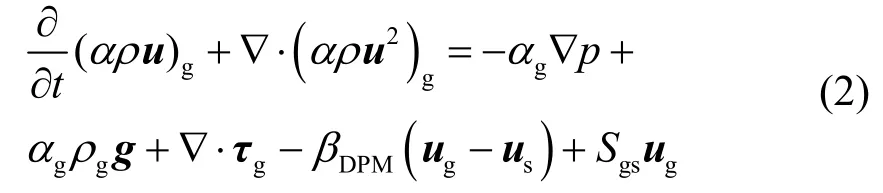
其中,p为气体相的压力;g为重力加速度;βDPM为单位体积气固之间曳力的总和,根据Gidaspow提出的模型,表示为:
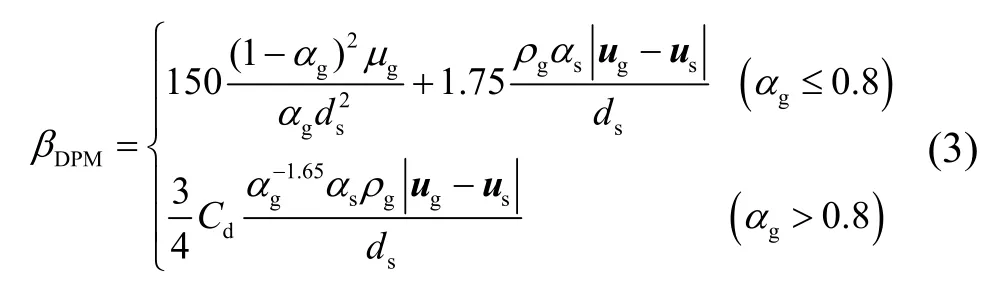
其中:
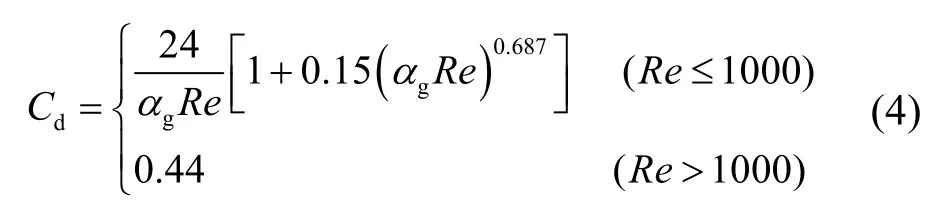
式中,ds为固相颗粒直径;μg为气相动力粘度;Re为颗粒雷诺数,表示如下:
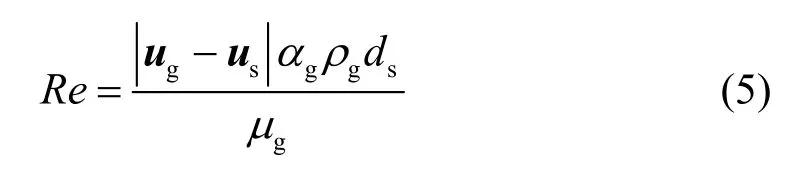
式(2)中τg为气相的应力张量,根据应力应变本构关系可以表示为:
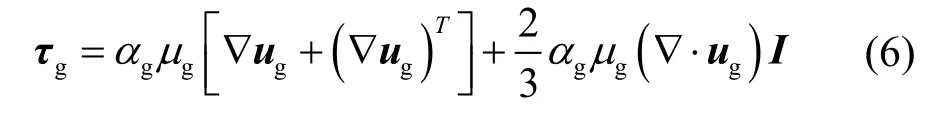
其中,μg为气体动力粘度,包括层流粘度与湍流粘度两个部分。
2.3 连续相能量守恒方程
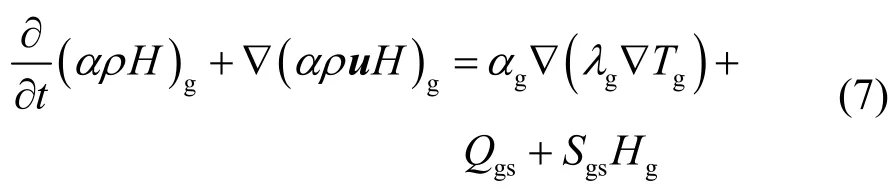
其中,H为相的焓值;Qgs为气固两相间的对流传热。
2.4 连续相组分输运方程
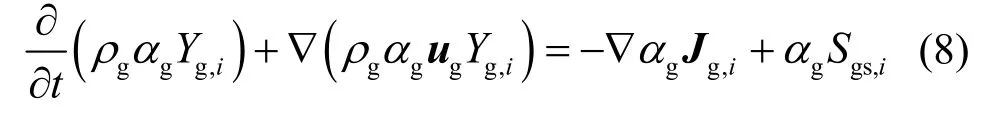
其中,Y为气体相中各组分的质量分数;下标i依次表示各个组分;αgSgs,i为来源于反应等原因的源项;Jg,i为第i组分的扩散通量。
2.5 颗粒相拉格朗日运动方程
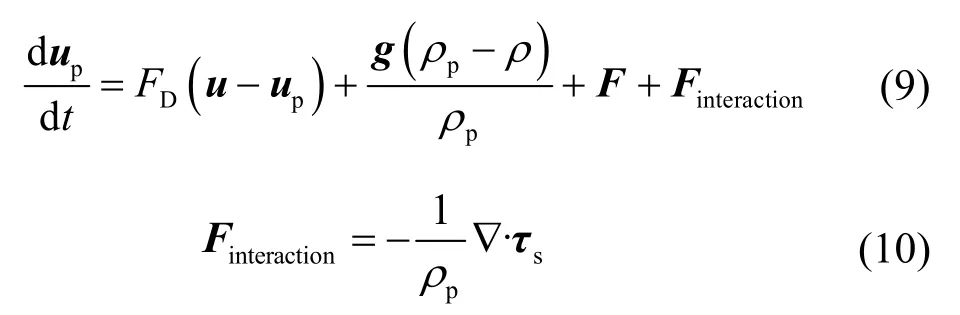
式中,下标p代表颗粒相;up为颗粒的速度矢量;FD为颗粒相所受到曳力的曳力系数;F为其他作用力源项;Finteraction为颗粒之间的相互作用;τs为颗粒相的应力张量,表示为:
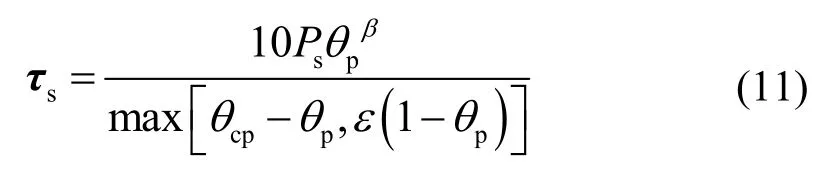
其中,Ps为压力量纲的常数;θp为固体体积分数;β是介于2~5之间的参考常数;θcp表示固体体积分数压缩极限。
2.6 颗粒相能量方程
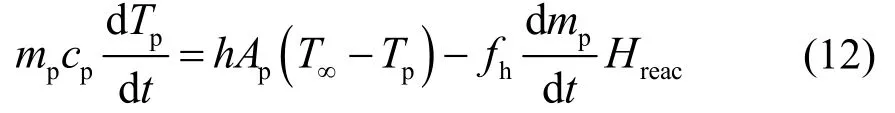
其中,下标p代表颗粒相,方程左侧代表单颗粒粒子的温升,m、c、T分别为单个颗粒质量、比热容以及温度。右侧第一项代表气固换热量,h为换热系数,第二项代表反应放热被颗粒吸收的量,其中fh为热量传递系数,Hreac为反应放热量。
3 结果与讨论
3.1 模拟结果验证
通过模拟结果与实验结果的对比,可验证模拟结果的可信度。本文中,压力是在实际运行过程中和模拟过程中均可获得的参数,并且是衡量循环流化床锅炉运行状态的关键参数,对沿炉膛高度方向的实验和模拟平均压力值进行对比,结果如图5所示。对于沿炉膛高度的压力变化,实验值和模拟值呈现相同的趋势,随着高度的增加,压力逐渐降低,并且单位高度的压降也随高度的增加呈减小的趋势。对于每个测压点,实验值均要高于相同位置下的模拟值,差值在200~700 Pa之间,偏离范围在6%以内,因此可以认为实验数据与模拟结果吻合较好,说明了数值模拟结果具有可靠性。而实验测压点测得的压力均高于模拟值,其原因可能是实际运行中床料要比模拟时的床料多和燃烧产生的气体造成的床内压力偏差。
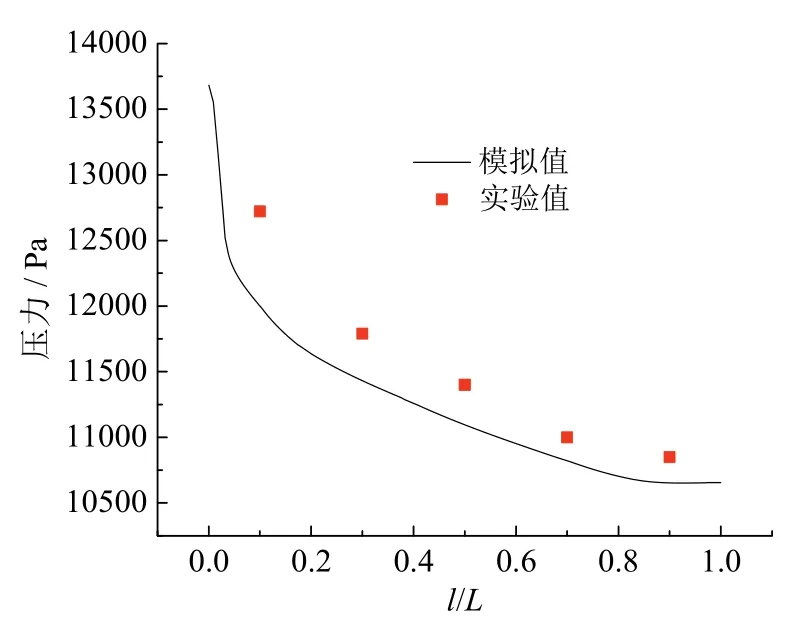
图5 沿炉膛高度方向实验和模拟压力值对比Fig. 5 Comparison of pressure between experiment and simulation along the height of furnace
3.2 固相体积分数和颗粒速度分布
在循环流化床锅炉中,炉内的气固流动状态对传热传质效果及锅炉的稳定运行至关重要,图6所示为模拟过程稳定运行到40 s时,循环流化床锅炉内部颗粒的固相体积分数分布情况。在CPFD模拟中,采用计算颗粒的方式来减少计算量,所以图中的一个颗粒相当于实际情况下由性质相近的若干颗粒组成的一个颗粒群,同时由于分辨率的原因,图中计算颗粒粒径尺寸显示与实际颗粒尺寸有所差别。从图中可以看出,在炉膛内部气固流动稳定后,循环流化床锅炉床料循环建立并达到稳定状态。炉膛底部(主要集中在锥形段)为一定高度的密相区,这与实际炉膛中监测的密相区高度相近;另外,在密相区内,后墙壁面附近会发生床料富集的现象,这主要受到回料腿返料的影响。随着炉膛高度的增加,床料固相分数逐渐降低并进入稀相区,稀相区内的床料分布较密相区更为均匀,并且回料腿对床料分布的影响减弱。稀相区内一部分床料颗粒在气流曳力的作用下被携带上升,进入旋风分离器入口,另一部分贴近壁面的颗粒由于气流携带能力不足,呈现下降的流动状态。在此运行工况下,通过模拟得到了稳定运行状态下炉膛内的固体循环流量为3 218 kg/s,经过旋风分离器分离后从每个回料阀返回的床料流量平均为1 065 kg/s,对3个旋风分离器入口的气固质量流量的不均匀性进行分析,如图7所示。
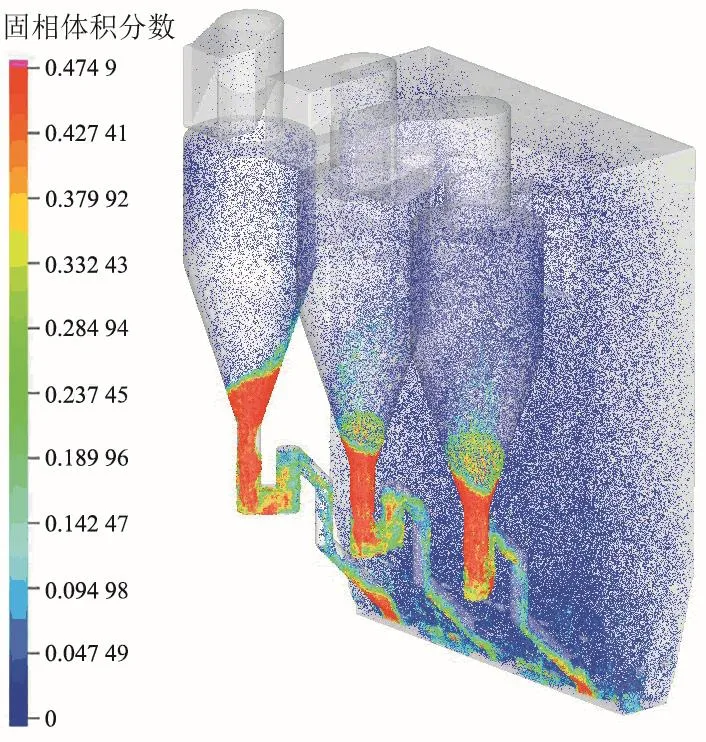
图6 稳定状态下床料分布图Fig. 6 Distribution of solid volume fraction under steady state
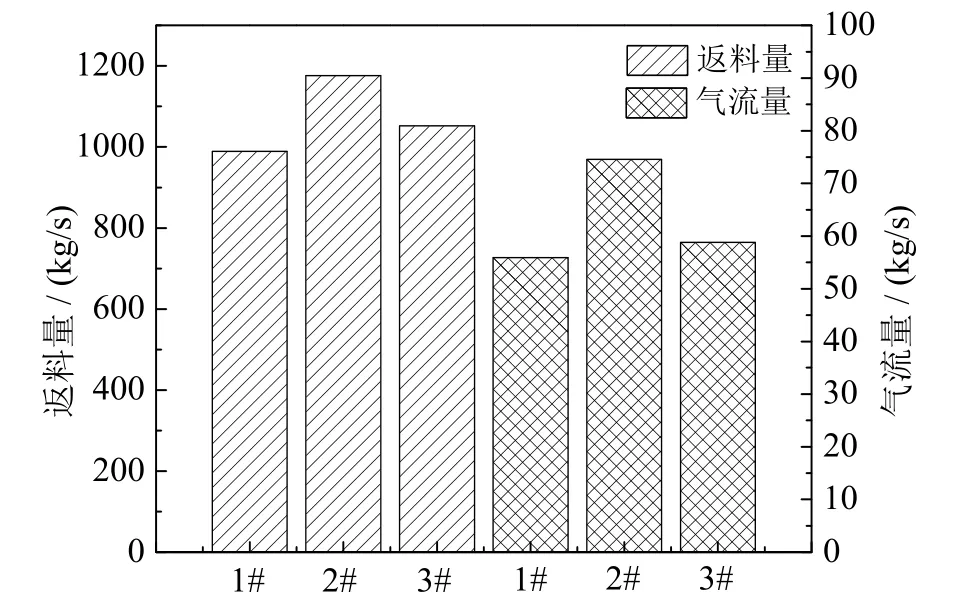
图7 旋风分离器入口气固质量流量不均匀性Fig. 7 Heterogeneity of gas and solid mass fluxes at cyclone inlets
达到稳定状态后的各个旋风分离器入口气固流动都很稳定,质量流量波动幅度很小,说明循环流化床锅炉的工作状态很稳定。在3个旋风分离器中,2#旋风分离器入口的固相质量流量要明显高于1#和3#(旋风分离器标号见图1),偏差率分别为5.76%和3.85%,2#和3#入口处固相质量流量相近但3#要略高一些,偏差率为1.93%。 而气相不均匀性同固相类似,2#旋风分离器入口的气相质量流量要明显高于 1#和 3#,偏差率分别为 9.87%和8.33%,2#和3#入口处固相质量流量相近,但3#要略高一些,偏差率为1.54%。
在稳定运行的工况下,进入旋风分离器的床料在旋风分离器中进行气固分离,提供了循环流化床锅炉稳定运行的基础。从旋风分离器物料出口端分离的床料进入下降管,然后进入回料阀的输运室,其物料产生的堆积压力足以克服循环流化床锅炉内部和旋风分离器间的压差,从而保证循环流化床系统的稳定运行。返料室的床料处于鼓泡流化态,颗粒越过返料口进入回料输运管路,完成循环。截取炉膛正中垂直于前墙(规定炉膛靠近旋风分离器的一侧为后墙,相对一侧为前墙)的一个面进行分析,如图8所示,可以看到整个模拟过程中,初始时刻回料阀中床料堆积,形成了料封。在0~20 s之间,由于还没有达到稳定运行的状态,从旋风分离器分离下来的床料少于送回炉膛的床料,因此回料阀中的料封不断降低,当回料阀的进出口床料的流量逐渐趋于一致时,回料阀的运行达到稳定(如在30 s呈现的运行状态)。同时,输运室处于鼓泡床状态,气泡以贴壁逃逸的形式流出,但是如果在锥形段内存在床料,气泡不可能在锥形段内斜向上贴壁逃逸,而是汇聚在中央,由于短时间内突破不了锥形段内床料的封锁,所以会使气泡在与锥形段相连的颈部不断积聚,出现节涌的现象,直至破开床料层。分析节涌现象的原因,是由于输运室竖直段的高度较低,其内的料封不足以克服炉膛和旋风分离器之间的压差,所以床料渐堆积至锥形段内,但最终锥形段内的床料阻碍了气泡的溢出,出现节涌的现象。节涌现象不利于回料阀的稳定运行,因此应使稳定运行时输运室的料封不进入锥形段中为宜,从减小输运室中床料高度的角度出发来避免节涌的出现,例如增加回料阀输运室竖直段高度、减小炉膛和旋风分离器之间的压差等。
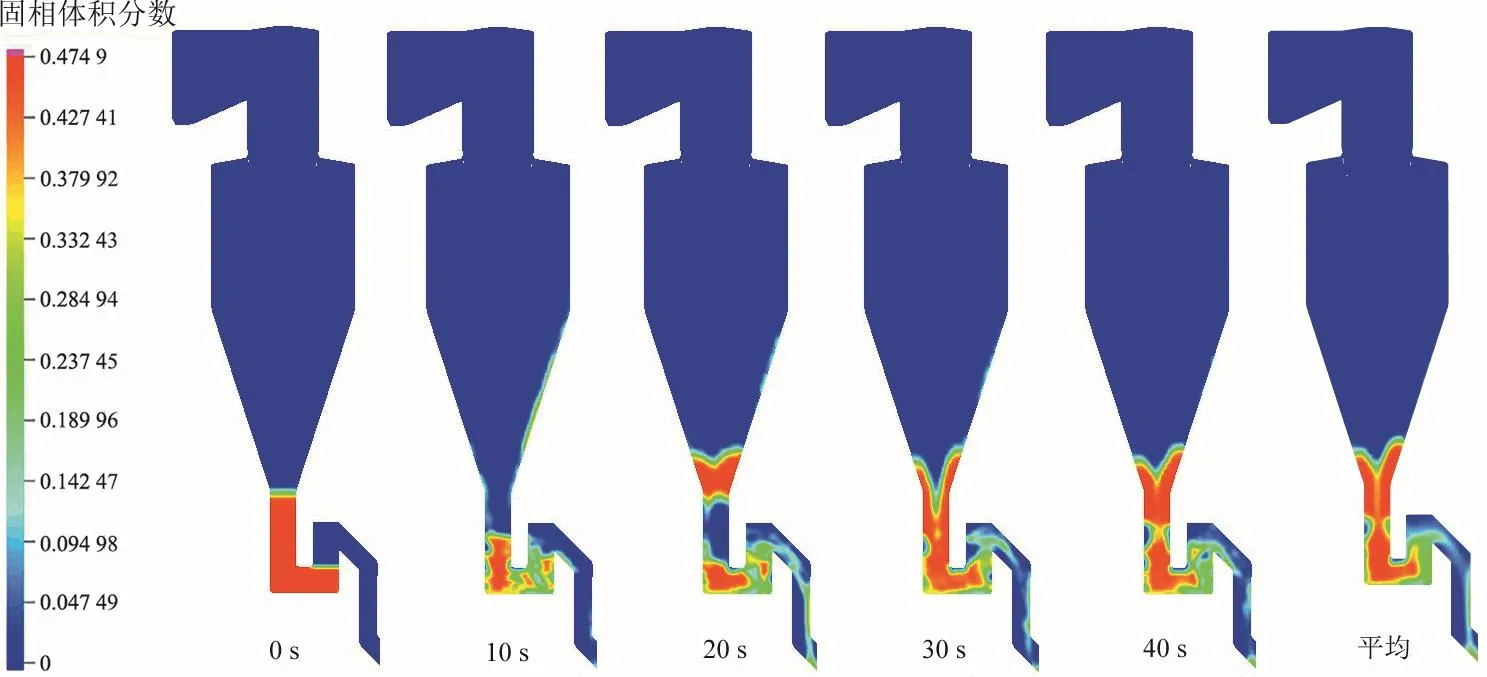
图8 稳定状态下回料阀正中截面固相体积分数Fig. 8 Profiles of solid volume fraction on the central section of loop seal
根据模拟结果,分析沿炉膛高度方向上固相体积分数分布,如图9所示。炉膛内的气固流场明显分为下部密相区和上部稀相区两部分:对于颗粒浓度分布,在密相区内随着循环流化床高度的增加,床料固相体积分数迅速从0.022 5减至0.002 5,并且密相区的高度为2.5 m左右,仅为炉膛底部锥形区的1/3。高度大于2.5 m后为稀相区,固相体积分数随高度变化不大,平均固相体积分数为0.001。
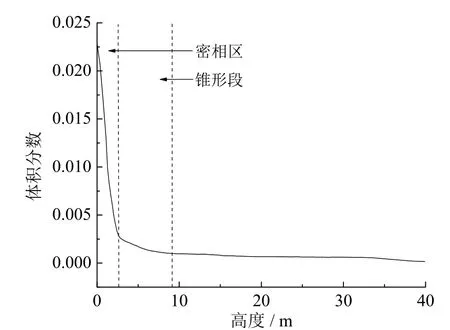
图9 沿炉膛高度方向时均固相体积分数分布Fig. 9 Distribution of time-averaged solid volume fraction along the furnace height
图10为炉膛正中平行于前墙的截面在不同高度下的固相体积分数分布,对截面宽度进行归一化处理,d/D= 0.5处为截面正中。平行于前墙的床料分布呈现对称的状态,密相区内床料在炉膛中的分布明显受到回料阀回料出口位置的影响(例如L= 0 m和0.5 m),由于颗粒被返料风吹向两侧,回料口间的固相体积分数较高。局部颗粒浓度过于集中有可能导致该位置温度偏高、反应器壁磨损加快和燃烧不完全等情况。随着循环流化床高度的增加,当高度大于1 m后,截面固相分布逐渐均匀,回料口造成的固相浓度不均匀性逐渐减弱。
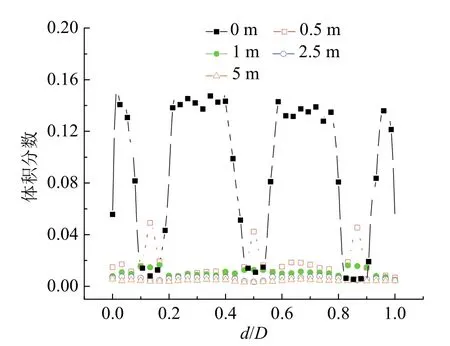
图10 平行于前墙炉膛正中截面不同高度下的时均固相体积分数Fig. 10 Time-averaged solid volume fraction of different heights on the central furnace section paralleling to the front wall
垂直于前墙的炉膛正中截面固相体积分数的分布如图11所示。在密相区下部(0~1 m)床料的分布受到回料口的影响,颗粒被返料风吹向前墙,因而峰值向前墙方向偏移,比较0 m、0.5 m、1 m三组数据可知,随着高度的增加峰值偏向前墙的程度更高。在2.5 m之后床料分布则呈现U形分布,靠近前墙和后墙的区域由于气流携带颗粒的能力不足,床料体积分数较高,而在中部则明显较低。
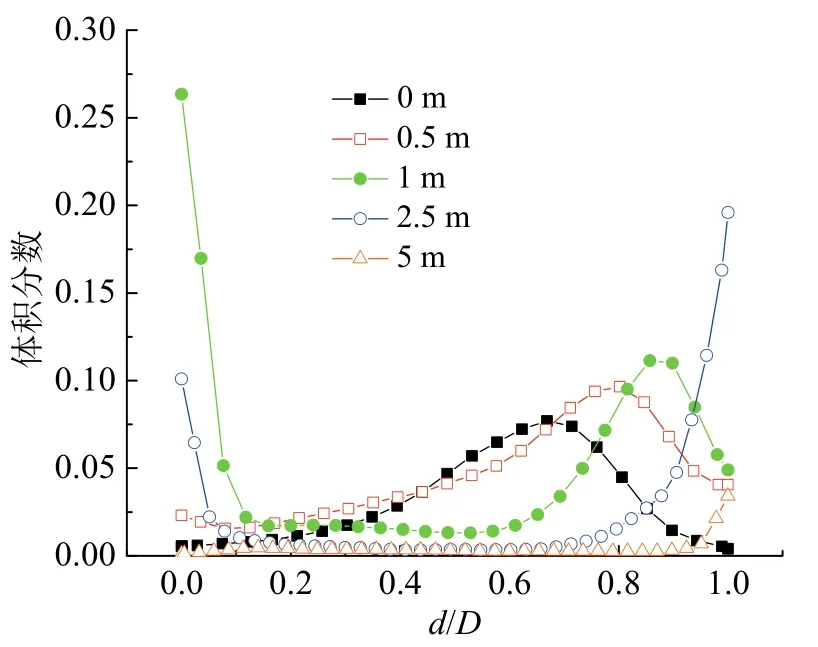
图11 垂直于前墙炉膛正中截面不同高度下的时均固相体积分数Fig. 11 Time-averaged solid volume fraction of different heights on the central furnace section vertical to the front wall
图12和图13给出了炉膛中平行于前墙和垂直于前墙的正中截面上颗粒轴向速度分布曲线,速度为正值表明颗粒向上流动,负值表明颗粒向炉膛底部回流。从图12中可以看到,平行于前墙的轴向速度在密相区内为对称分布,且随着高度的增加,这种对称性逐渐弱化,密相区内速度分布的对称性来自炉膛底部密相区内二次风和回料腿的对称放置;不同高度下的轴向速度随着高度的增加呈现先增大后减小的趋势,颗粒的轴向速度在 1 m处达到最大;与平行于前墙的固相体积分数分布不同,密相区内回料口间的区域颗粒速度低,但是靠近回料口的位置速度高,同时靠近回料口的颗粒速度分布出现两个峰值,峰值间的颗粒速度较低。
对于垂直于前墙的颗粒轴向速度,密相区内靠近前墙的一侧颗粒速度为负,颗粒向炉膛底部回流,靠近后墙一侧的颗粒速度为正,颗粒向上流动,稀相区则呈壁面附近低而中心区域高的分布趋势,近壁区存在明显的颗粒回流;随着高度的增加,颗粒轴向速度先增大后减小,在1 m处出现最大值,这与平行于前墙的颗粒轴向速度一致。
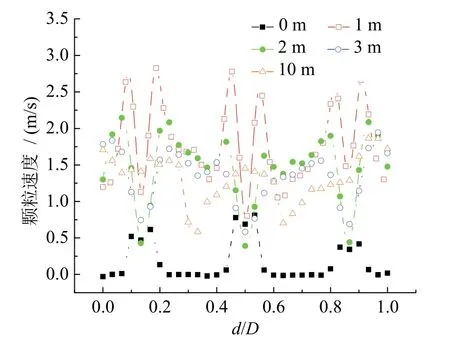
图12 平行于前墙正中截面不同高度下的时均固相速度分布Fig. 12 Time-averaged solid velocity distribution of different heights on the central furnace section paralleling to the front wall
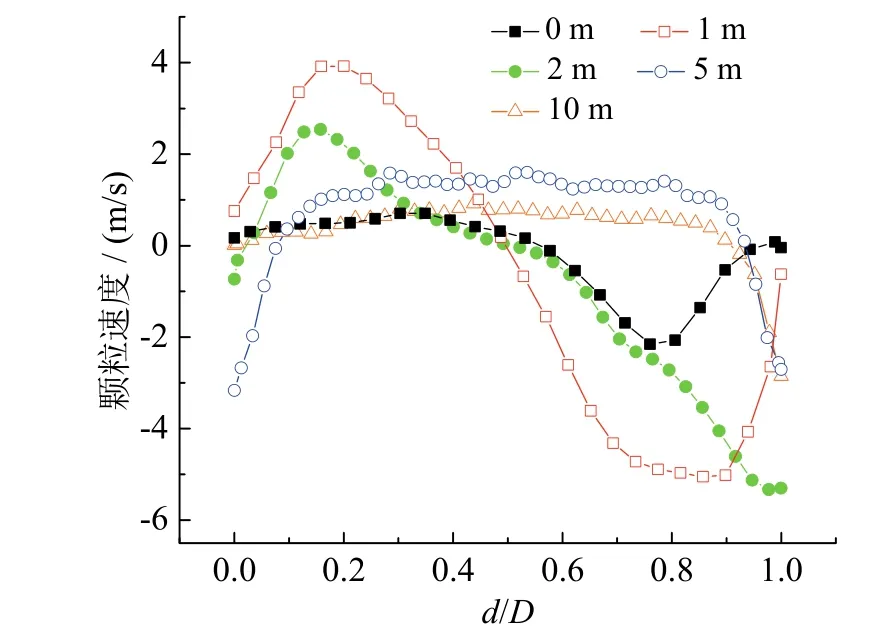
图13 垂直于前墙方向正中截面不同高度下的时均固相速度分布Fig. 13 Time-averaged solid velocity distribution of different heights on the central furnace section vertical to the front wall
3.3 压力分布
图14为稳定运行状态下炉膛的平均压力分布情况,可以发现整个循环流化床的压力分布呈现对称状态,同时回料阀的压力最高,炉膛的压力其次,旋风分离器中压力最低,并且左右两个回料阀底部的压力要高于中间的回料阀。回料阀的高压降有利于形成稳定的料封,克服循环流化床内部的系统压差。结合图 15的循环流化床锅炉内的压力平衡分布进行分析,其中压力值为系统内炉膛、旋风分离器、回料阀、料腿等部件中心线上的时均压力值。压力平衡对于循环流化床锅炉十分重要,一方面维持系统回路内的气体和颗粒循环,另一方面也确保全回路无气体泄漏。由图可见,炉膛内压力在密相区内梯度较大,其后压降在密相区和稀相区交界处发生转捩并保持稳定,这和床料的分布一致,炉膛内的压降为3 028 Pa;从炉膛到旋风分离器,压力仅在交界处的收缩段发生变化,下降了4 800 Pa;旋风分离其中的压力梯度基本为 0,只在靠近出口的位置发生了波动;在回料阀和旋风分离器交界处压降急剧增大,这是由于回料阀内下行颗粒大量聚集和流动密封阀输运室的松动风逆向流动所致,浓度明显增加,引起了压力的突变,在此之后回料阀内压降基本不变。回料阀输运室内压降为39 267 Pa,返料室内压降21 885 Pa;压降大,有利于颗粒的稳定输运。图 15显示水平孔口的压力值大于返料管出口的压力,因此,可判定流动密封阀能起到良好的气体隔绝作用。之后压力沿着料腿逐渐减小,直至进入炉膛密相区。压力平衡图从另一个角度体现了循环流化床锅炉内良好的颗粒循环情况。
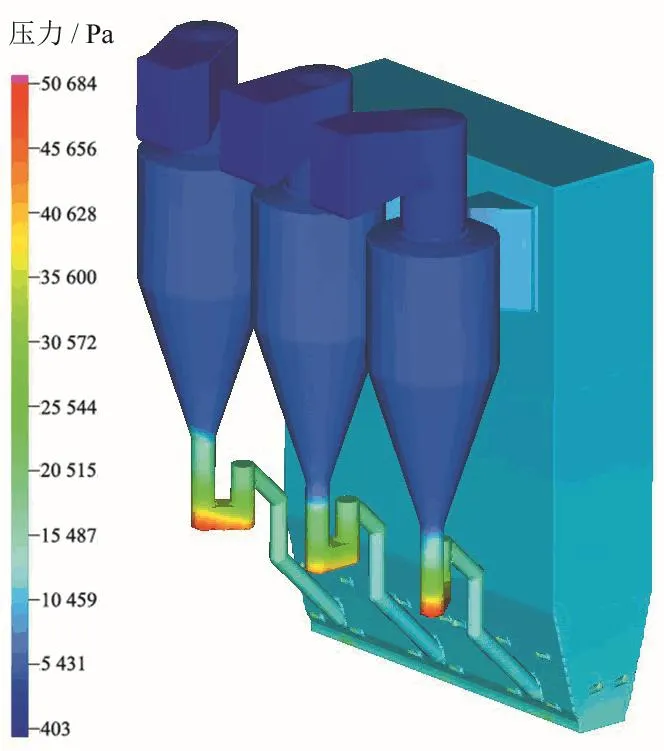
图14 循环流化床时均压力分布图Fig. 14 Time-averaged pressure distribution of the CFB
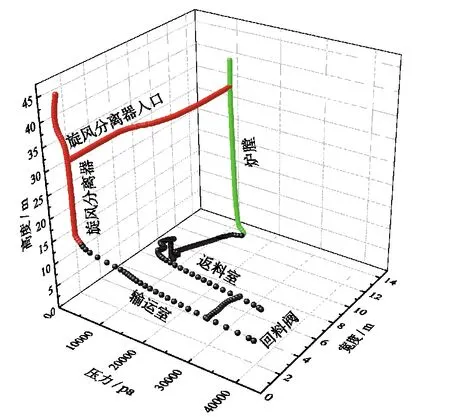
图15 循环流化床锅炉的压力平衡Fig. 15 Pressure balance of the CFB
4 结 论
本文对300 MW循环流化床锅炉进行CPFD模拟,主要关注了炉膛内的流化情况,获得了实验难以测得的关键参量:固相体积分数分布、颗粒速度分部、压力分布。可以得出以下结论:
(1)对于固相体积分数和颗粒速度分布,发现在炉膛内形成了明显的密相区和稀相区,在密相区内颗粒浓度和速度受到回料腿的影响而在水平方向上发生波动,随着高度的增加,这种影响逐渐减弱。
(2)对于压力分布,炉膛内的压降为3 028 Pa,其趋势与固相体积分数分布一致。而回料阀至旋风分离器这段内的压降主要集中于回料阀,回料阀输运室内压降为39 267 Pa,返料室内压降21 885 Pa。
(3)通过模拟得到了稳定运行状态下炉膛内的固体循环流量为3 218 kg/s,经过旋风分离器分离后从每个回料阀返回的床料流量平均为1 065 kg/s。
(4)分析回料阀的运行情况,发现达到稳定状态的回料阀返料室流化程度较高,而输运室流化程度较小,呈现鼓泡床状态,气泡大都贴壁逃逸并在回料阀和旋风分离器交界颈部处积聚,直至破开料封。
本文CPFD模拟结果可为循环流化床锅炉运行过程中的循环流量和流动密封阀的运行参量等操作参数提供可视化的理论指导,进而确保循环流化床锅炉的高效和稳定运行。
