汽车用液化天然气气瓶颈管应力校核方法研究

古纯霖

（中国特种设备检测研究院 北京 100029 ）

引 言

天然气作为一种优质、高效、清洁且储量丰富的低碳能源，对于增加能源多样化供应、优化现有能源结构、保护自然生态环境具有重要作用[1]。近几年天然气产业发展迅速，汽车用液化天然气气瓶行业也随之蓬勃发展。目前，汽车用液化天然气瓶的公称容积已由原来的500 L扩容到1 000 L[2]。扩容带来的最主要难题就是内胆前后端的支撑结构参数设计。按照传统的校核方法，仅对内颈管内胆外露部分进行应力校核，忽视了对内胆内部以及外颈管的应力校核，这使得上述两位置的参数设计存在盲目性。本文通过引入内外颈管变形协调的几何方程，使得内颈管内伸部分以及外颈管的受力状况得以求解，从而使汽车用液化天然气气瓶的前端支撑部位的尺寸参数设计更加科学合理。

1 载荷分析

图1为典型的汽车用液化天然气气瓶结构图[3]。由图可知，气瓶内胆重量完全依靠前端颈管及后端支撑棒支撑。对内胆组件进行受力分析，由于右端支撑棒处存在活动间隙，故将其简化为简支结构，即只有向上支撑力，无弯矩，从而可得内胆组件承受载荷状况如图2所示。

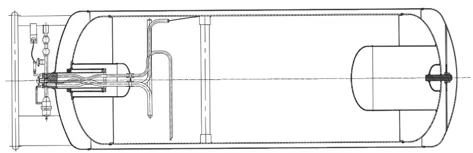
图1 汽车用液化天然气气瓶的常见结构

图2 内胆载荷分析图

根据内胆受力状况可得：

式中：G作用点为重心位置，G取值根据振动试验要求确定。对于容积不大于500 L的气瓶，振动试验要求加速度为3g，考虑到振动时有放大作用（一般在2倍以内），可取G为气瓶内胆及液体总重量的6倍；对于容积为500 L至1 000 L的气瓶，由于振动试验要求为5 g[2]，可取为气瓶内胆及液体总重量的10倍。M1、F2分别为分配头对内颈管的作用力及弯矩，F1为右侧支撑结构对气瓶的支撑力，L1为内胆重心到内颈管左端的距离，L2为内胆重心到右侧支撑结构位置。

对颈管组合支撑结构进行受力分析，颈管受力如图3所示。

图3 颈管组合结构受力分析图

由图3所示受力情况可得：

式中：M2、F3分别为内胆封头对外颈管作用的弯矩和力；L3为内颈管左端与外颈管左端的距离。

单独对外颈管进行受力分析，受力状况如图4所示。

由图4可得：

式中：F5、M3分别为内外颈管连接环对外颈管作用的力和弯矩；F4为玻璃钢环对外颈管作用力；L4为外颈管长度。

单独对内颈管进行受力分析，分析受力情况如图5所示。

图4 外颈管受力分析图

图5 内颈管受力分析图

由图5受力情况可得：

式中：F7为玻璃钢环对内颈管的作用力；M4、F6分别为内外颈管连接环对内颈管作用的弯矩和力。

由于已经对内外颈管整体进行了静力和弯矩平衡计算，故上述两个方程为无效方程。

根据玻璃钢垫环的受力平衡可得：

根据内外颈管连接环受力及弯矩平衡可得：

根据上述受力分析可知，有M1～M4、F1～F7共11个未知数，却只有9个有效方程，无法求解，故该结构为静不定结构，需要引入几何方程[4]。

2 内外颈管弯矩分布分析

根据外颈管受力图，可绘制其所受弯矩分布图，如图6所示。

图6 外颈管弯矩分布图

由图6可得外颈管弯矩分布方程：

Mx=M2+F5×x

式中：M2为距外颈管左端的距离；通过积分可得：

E1I1ω=M2× x2/2+F5× x3/6+C × x +D

由于x=0时，ω=0，ω＇=0。

故有：ω=（M2× x2/2+F5× x3/6）/E1I1

式中：ω为外颈管挠度；E1为外颈管的弹性模量；I1为其惯性矩。

根据内颈管受力图，可绘制其所受弯矩情况，如图7所示。

由图7可得外颈管弯矩分布方程：

Mx=M1+F2× x（x≤L3）

Mx=M1+F2× x-F6×（x-L3）

（L3≤x≤L3+F5）

式中：x为距内颈管左端的距离。

通过积分可得：

图7 内颈管弯矩分布图

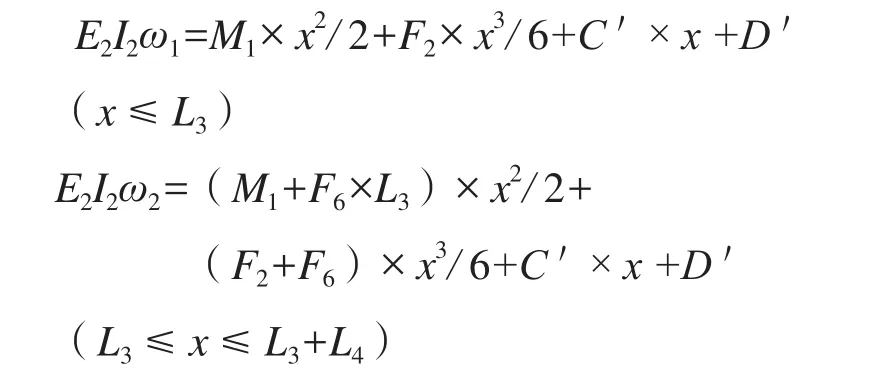
式中：ω1、ω2为内颈管挠度；E2为内颈管的弹性模量；I2为其惯性矩。

由于x =0时，ω1=0，ω1＇=0。

故有：

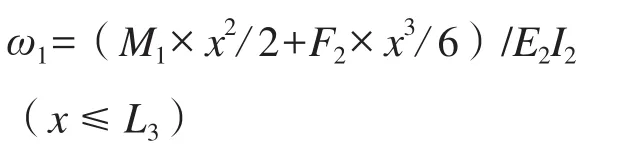
由于当x =L3时，ω1=ω2且ω1＇=ω2＇。

故有：C＇=-F6×L23/2，D＇=F6×L33/6

可求解得：

3 几何方程分析

外颈管变形状况分析：

根据外颈管的弯矩分布状况，可得到其变形状况如图8所示。

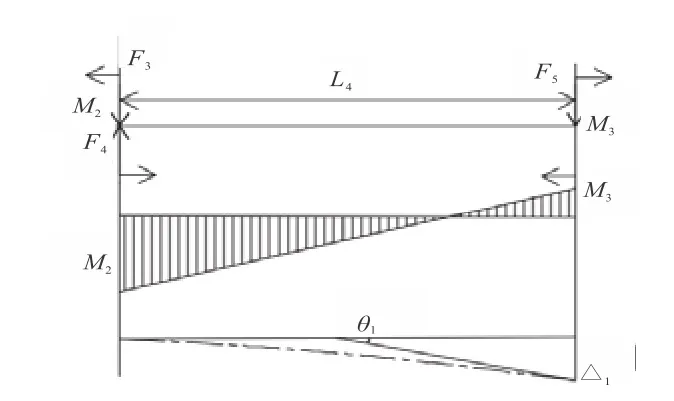
图8 外颈管变形状况图

图中：θ1为外颈管右端变形的切向角度；△1为外颈管右端变形挠度。

根据内外颈管的弯矩分布状况，可得到其变形状况如图9所示。

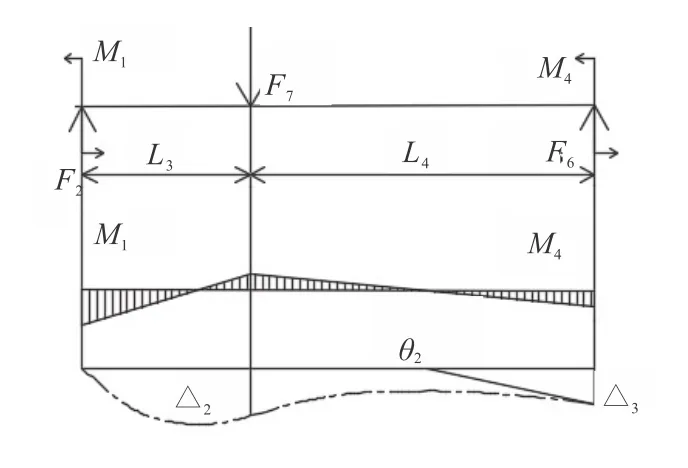
图9 内颈管变形状况图

图中：θ2为外颈管右端变形的切向角度；△3为外颈管右端变形挠度；△2为外颈管左端与内颈管对应位置的变形挠度。

由于内外颈管的右端相连，故该位置处两只颈管的位移相同，弯曲角度相同。

故有：

式中：

将方程（1）～（11）联合求解，即可得到M1～M4、F1～F7。

结 语

本文首先对汽车用液化天然气气瓶颈管支撑位置进行了静力和弯矩分析，发现该结构为静不定结构，仅仅采用静力和弯矩平衡无法求解，需要引入几何方程；然后分别对内外颈管的弯矩分布进行了分析，得到了内外颈管弯曲挠度方程；最后通过分析内外颈管连接的几何特点，得到了内外颈管连接端部位置的挠度及弯曲角度相等的几何关系，使得内外颈管受力方程得到求解，为汽车用液化天然气气瓶内外颈管尺寸参数的设计提供了可靠的计算方法。