基于层次分析法解决“互联网+”时代的出租车资源配置

　　　

最近几年，打车贵、打车难，经常成为居民、新闻媒体议论的话题。某城市居民普遍反映打车价格偏高，而另一方面，由于经营权的有价性、出租车资产专用性、买断经营、违规转让、寻租严重导致出租车司机劳动强度大、竞争压力大，但收入却相对偏低的情况。目前又由于打车软件的盛行，导致出租车空载率高，拒载，乱收费等情况日益严重，甚至经常发生出租车司机集体罢工以反抗打车软件盛行的现象。这反映出政府对出租车的管理存在一定的问题，现有的出租车定价不够合理、拒载、乱收费情况严重，导致空载率过高，整个出租车行业不景气，长此以往将影响社会的稳定，所以打车难这一问题值得关注。在未来一段时间内，我国城市规模会不断扩大，人口会不断增长，人民生活水平将不断提高，对出租车的需求也会不断变化.如何根据出租车服务水平、客户需求以及外部环境，计算出不同时空出租车资源的“供求匹配”程度，规划出合理的租车数量，从而缓解打车难这一现象。

问题1的求解

1.建立层次结构

问题的层次结构如下：第一层目标层(O)；第二层准则层(C)；第三层措施层(P)。

2.确定准则层(C)对目标层(O)的权重W

现对“匹配供求”率的问题进行层次单排序，为求出Q1、Q2、Q3在目标层中所占的权值，构造目标层到准则层的判断矩阵：

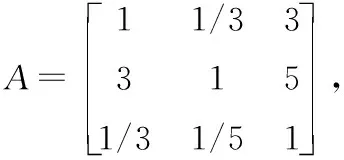
3.确定措施层(P)对准则层(C)的权重

根据问题的条件和模型的假设，乘客的各项条件按统一原则均可量化，而且能够充分反映出乘客对出租车的需求量，由此可以分别构造措施层(P)对准则层(C)的比较矩阵，同上分别求S、t、m在Q1、Q2、Q3的权值，得到：

WQ1=(0.2,0.4,0.4)T，WQ2=(0.258,0.637,0.105)T，WQ3=(0.4545,0.4545,0.091)T

从而可以得到措施层(P)对准则层(C)的权重W2=(WQ1,WQ2,WQ3)T。

4.确定措施层(P)在目标层(O)中的组合权重

设上一层次(A层)包含A1，…，Am共m个因素，它们的层次总排序权值分别为a1，…，am。又设其后的下一层次(B层)包含n个因素B1，…，Bn，它们关于Aj的层次单排序权值为b1j，…，bnj(当Bi与Aj无关联时，bij=0)。现求B层中各因素关于总目标的权值，即求B层各因素关于总目标的权值，利用上述结论，我们可以得到组合权重W=(0.2337,0.5567,0.1796)T作为目标决策依据。

5.综合排序的结果分析及说明

接受层次分析结果，可知，不同时空出租车资源的“供求匹配”程度受路程段、时间段、小费的影响，权重依次为23.37%，55.67%，17.96%。由此可以得到15位乘客的排序方案。

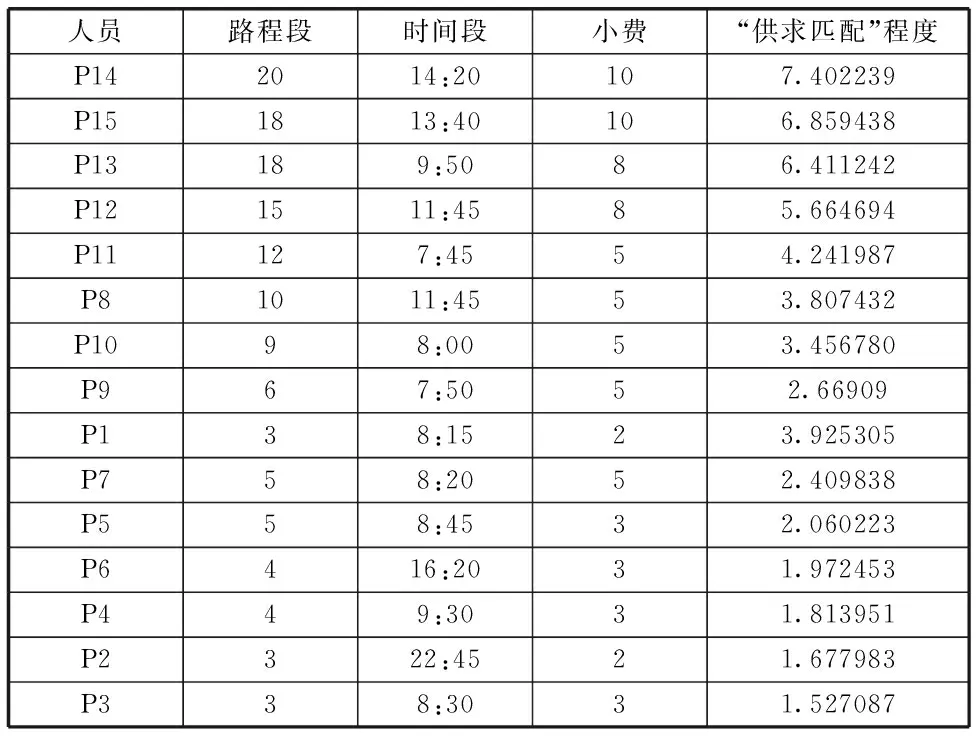
表1　15位乘客打车排序结果

15位乘客打车排序结果(表1)

由该表可知，当有12辆出租车接单时，前12位乘客能搭到车，空载率为20%；当有9辆出租车接单时，前9位乘客能搭到车，空载率为40%；当有6辆出租车接单时，前6位乘客能搭到车，空载率为60%。因此，要提高不同时空出租车资源的“供求匹配”程度，就是要提高出租车司机的接单率。

问题2的求解

某软件有一个非常重要的好玩之处，比如3个司机同时抢一个用户，该软件能判断出这是一个好活，如果用户叫车10多秒后才有司机响应，说明不是一个好活。如果两分钟后还没司机应答，终于有一个司机应答，我们就给他补贴，加到一定程度后发现仍没人抢单，此时用户已呼叫三次，我们直接给司机加钱，5元、8元、10元一直加到最高16元，附近司机看不到1公里便去拉人，16元轻松进口袋，用户能听到“这一单是由该软件为你奖励的司机16元”。由上可假设前面讨论的15位乘客都使用了该打车软件，因此可将这15位乘客分为5个区间，进行不同程度的补贴；使x=5，8，10，13，16元；分别对应表2中的15位乘客(以3个乘客为一个分段)。

通过计算15位乘客对应于出租车的单位时间盈利及之前的顾客能打到车的匹配程度综合分析来判断该公司的补贴方案是否对“缓解打车难”有帮助。

1.假设出租车的运价、经营成本及单位时间盈利

根据某城市出租车定价可知，晚上10点以前，出租车的价格为3公里以内8元，10点以后，出租车价格统一上升20%，同时，某城市出租车使用93号汽油，假设该汽油油价不变，燃油价格7.5元/L，平均单位里程耗油0.1L/km，时间段与出租车的平均行驶速度关系如下：假设高峰段，出租车的平均行驶速度为25km/h，其他时间，出租车的平均行驶速度为35km/h，利用上述假设我们可以得到出租车的单位时间盈利计算公式：y=(M-C+x)/(60×s/v)

注：M是出租车运价，C是出租车运营成本，x是补贴方案，s是行程，v是行驶速度。

2.各公司的出租车补贴方案对缓解打车难的帮助

我们可以通过问题一中15名乘客使用上述模型后，结合以上的分析结论，得到出租车司机载单个乘客单位时间(分钟)的盈利如下：

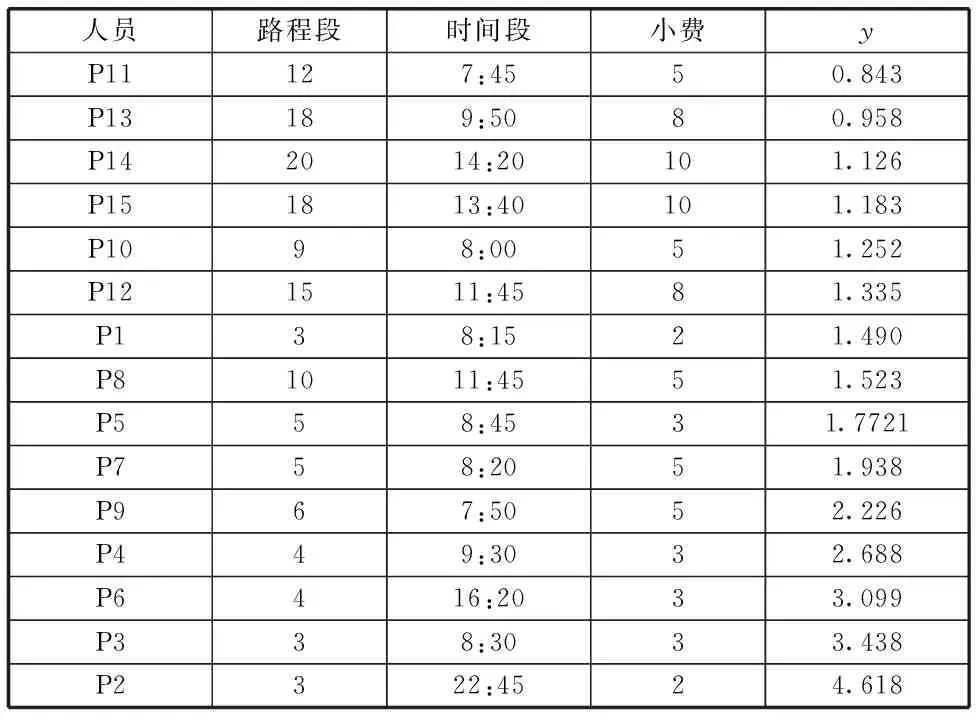
15位乘客对应的出租车单位时间盈利

将表2与表1 进行比较，可以看出，乘客P11，P13，P10，P1，P5，P4，P3，这7位乘客经过使用打车软件后，在一定程度上缓解了打车难的问题。但对另外8位乘客来说改善并不大。这说明各公司的出租车补贴方案虽然对部分乘客在“缓解打车难”问题上有一定帮助，但是涉及的人数不是很多，波及范围并不广。

问题3的求解

1.路程补贴

因为路程越短，y越大，所以短路程不予以补贴，路程越远，补贴越多。假设的补贴方案如下表所示：

路程km每增加1km所补贴的金额n10～505～100.510～15115～201.5

n1：每增加1km所补贴的金额，据分析，出租车司机载上述15名乘客，所获单位时间内的盈利y分别为

y1=0.7986；y6=0.9917；y11=0.9576；

y2=1.4292；y7=0.6542；y12=1.0053；

y3=0.7986；y8=0.9100；y13=0.7755；

y4= 0.7083；y9=0.9139；y14=1.1258；

y5= 0.6541；y10=0.6505；y15=1.0856

2.时间段补贴

由以上分析可知，在该城市上下班高峰期时，出租车司机载一位乘客单位时间内的盈利较大，故不予以补贴；而在其他时间段，因公交地铁等交通工具的充足，故予以补贴。假设上班高峰期，补贴金额为0元；其他时间，每载一位乘客补贴5元，不考虑小费的影响，出租车司机载上述15名乘客，所获单位时间内的盈利y分别为

y1=0.7986；y6=1.3767；y11=0.9819；

y2=2.4014；y7=0.6542；y12=0.9881；

y3=0.7986；y8=1.0558；y13=0.4977；

y4=0.7083；y9=1.3514；y14=0.8342；

y5=0.6542；y10=0.5579；y15=0.8599

3.比较分析两种补贴方案的优劣

根据比较路程补贴和时间段补贴所得的出租车司机载一位乘客单位时间盈利的大小发现，通过时间段补贴所得的y相对于通过路程补贴所得的y大部分偏小，且波动较大。且通过路程补贴的y波动小，y值偏高，显得更加合理，并且能更好地提高出租车司机的积极性，从而较好的缓解打车难现在。故路程补贴的方案可行。

总结

1.模型的优点

1.1 本模型采用的层次分析，从目的入手，通过不同层次的分析，得出决定不同时空出租车资源“供求匹配”程度的三项指标；

1.2 从实际乘客的需求出发，将问题简化，并通过优化排序，较为系统地分析了各公司的出租车补贴方案对“缓解打车难”的影响；

1.3 结合问题一、二，对出租车的补贴方案进行了不同角度地设计，通过比较分析，得出了较为合理的补贴方案。

2.模型的缺点及改进

2.1 模型是以供给出租车的供给量不变，油价不变为假设的，但在实际过程中，这两个指标都有一定的波动；

2.2 模型以15名乘客为主要研究对象，数据较小，从而可能会导致误差偏大。

2.3 在补贴方案中，我们考虑的是单一因素的补贴，如果两个因素进行适当的权重分配，模型可能会更完善。

3.模型的推广

目前，社会存在的打车难，空载率高的现象，乘客路程过远，出行时段等而导致司机收入偏低，从而拒载引起的。通过路程补贴，增加司机在一位乘客单位时间的盈利，从而较为有效地解决出租车司机拒载，乘客打车难的现象，具有一定的可操作性。

(昆明理工大学津桥学院，云南昆明650093)

本文章依托基金项目：云南省教育厅科学研究基金项目(2015C107Y)及云南省教育厅科学研究基金项目(2014Y645)