有源诱饵的生存概率统计方法研究

刘　朋,王永海,刘国彬,沈　健

(中国洛阳电子装备试验中心，河南 孟州 454750)

0　引言

反辐射导弹作为电子战“硬杀伤”的一种手段，主要利用电子侦察技术对电磁辐射源进行探测、跟踪，进而自动实施攻击。为了提高雷达的生存概率，有源诱饵被广泛应用于反辐射对抗中，它通过在时域、能量域、空域、频域等方面对雷达进行保护，能够有效对抗反辐射导弹的攻击。

近年来，随着有源诱饵技术的发展，对有源诱饵的诱偏能力提出了更高的要求：希望有源诱饵不仅能保护雷达，还能够保护自身。在如何评估有源诱饵的生存能力方面，根据科研试验的实践经验，生存概率这一指标逐渐为各方所重视[1]。生存概率是相对命中概率而提出的。对反辐射导弹试验而言，考核的是命中概率；对雷达及有源诱饵试验而言，考核的是生存概率。本文就生存概率的统计方法进行探讨。

1　获取反辐射武器落点数据的途径

生存概率的统计基础是反辐射导弹的落点数据。根据科研试验的成本和武器系统鉴定的不同要求，可以采取不同的试验方法获取反辐射导弹的落点数据。

1.1　外场试验

1.1.1飞行器挂飞试验方法

飞行器挂飞一般是将反辐射导引头加装于飞行器上，雷达及有源诱饵按一定构型部署于阵地。飞行器按照预定航线飞行，通过数据记录设备记录反辐射导引头的测向结果以及飞行器的飞行姿态等信息[2]。

常用的飞行器挂飞试验方法包括固定翼飞机挂载反辐射导引头和无人驾驶飞行器挂载反辐射导引头进行的飞行试验。但因固定翼飞行器不能受反辐射导引头闭环控制，无法推算获得反辐射武器的弹着点，所以进行诱饵生存概率的统计时更多的是采用无人驾驶飞行器进行挂飞。

以飞艇挂飞试验为例。将反辐射导引头和无人驾驶飞艇构成闭环控制系统，能够使用反辐射导引头的测向数据控制飞艇的飞行轨迹，动态模拟反辐射武器的末端攻击过程；再结合反辐射武器的角分辨力、速度、过载等参数，即可推算反辐射武器的弹着点。试验过程中，当飞艇攻击目标时，在即将落地前将其拉起，进行再次的攻击，可以进行多次的飞行试验，便于得到充分的试验数据，然后利用数据推算得出弹着点并计算各辐射源生存概率。该试验方法易于组织，消耗低，风险小，可重复进行。

1.1.2外场实弹打靶试验

实弹打靶试验能够完全反映典型作战状态，置信度较高，可直观反映反辐射武器的攻击效果。与挂飞试验不同的是，打靶试验中导弹与目标均为一次性使用，所以导引头必须加装遥测信号来取得导引头的信号参数，其它地面测量手段与挂飞试验相同[3]。试验中，根据需求选择合适的置信度计算试验所需的样本量，之后，按照样本量组织一定次数的实弹打靶，并统计打靶中雷达及诱饵被命中的次数，即可得到在一定置信度情况下的辐射源生存概率。该方法为了保证统计的置信度，所需的实弹数量较多，使得试验成本较高。

1.2　仿真试验

反辐射武器仿真试验包括计算机数学仿真试验和半实物仿真试验，其优点为便于控制、试验灵活、重复性好，试验结果也便于分析[4]。但仿真试验需要准确的数学模型和外场试验数据对仿真模型进行验证，模型的逼真度较为关键，它直接影响试验的可信度。

1.2.1数学仿真试验

数学仿真是以数学模型为基础，即用数学模型代替实际的系统进行试验。其关键过程包括数学模型的建立和仿真模型的校验，而模型的校验往往需要利用外场试验结果进行，以验证模型的准确性。该试验主要利用计算机完成，需要将数学模型用程序语言表达为仿真模型[5]。试验过程中，仿真系统按照实战情况模拟整个作战过程，仿真模型的准确性能够确保反辐射武器、雷达和诱饵间位置关系与实际飞行的一致性，从而实现一条完整的仿真弹道。通过多次仿真试验获得反辐射武器的多个仿真弹道，得到其弹道点分布，完成各辐射源生存概率的统计。

1.2.2半实物仿真试验

半实物仿真试验是指在仿真试验系统的回路中接入部分实物的仿真，它用部分硬件替代相应部分的数学模型，尽可能地接近实际情况，从而得出更准确的结果。通常分为辐射式半实物仿真试验和注入式半实物仿真试验2类[3]。这2种方法均能完成对反辐射武器攻击过程的模拟，以及对雷达和诱饵毁伤情况的仿真。其试验过程与数学仿真试验基本一致，也是通过多次仿真试验获得反辐射武器的弹着点分布，用于对反辐射武器抗诱偏性能的评估。

2　生存概率统计方法分析

2.1　基于二点分布参数估计的统计方法

二点分布参数估计在电子装备试验中有着广泛的应用，它又被称为0-1分布[6]，即在统计反辐射武器攻击效果中只需统计落点位置是否命中即可，打中为“1”，打不中为“0”。该统计方法对二点分布参数的估计精度，可用一定置信水平下的置信区间长度表示，对于给定的置信水平和置信区间，能够确定统计所需的样本大小。也就是说为了获得高置信度的统计结果需要较大的统计样本量。若某诱饵生存概率的设计指标为90%，试验时选取置信水平95%、允许抽样误差±5%进行抽样，则所需的样本群为142次；同样的，若选取置信水平80%、允许抽样误差±5%进行抽样，则所需的样本群仅为62次。

根据飞行试验结果推算的弹着点位置，计算反辐射导弹弹着点与辐射源之间的距离。反辐射导弹的杀伤半径为Ra，雷达或诱饵车的安全工作半径为Rr，若落点与辐射源距离R满足：

R>Ra+Rr

(1)

则判定辐射源未被击中，否则被击中。

总有效试验次数为N，若辐射源被击中的试验次数为Mr，则该辐射源的生存概率为：

Pr=1-Mr/N

(2)

用上述公式统计各诱饵的生存概率易于实现，能够定量考核诱饵的诱偏效果。但是由于飞行试验过程具有很大的随机性，该统计方法不能够很好地排除试验随机因素的影响，无法充分评估导弹来袭过载中弹着点的分布规律。

2.2　基于正态分布概率密度函数的统计方法

二点分布参数估计虽然简单实用，但受试验次数限制其样本量有限，不能体现弹着点的分布规律。一般而言，反辐射导弹在攻击过程中，导弹的弹着点与多种随机因素有关，包括空域电磁信号环境、导引头工作状态、测角误差以及导弹控制误差等。通常若影响某个随机变量的因素较多，且每个因素的影响都很小，正常情况下都不起决定性作用，则这样的随机变量一般都近似服从正态分布，因此可认为导弹的弹着点服从正态分布[7]。因此，本文结合二点分布参数估计，通过统计计算弹着点的分布概率密度，得出有限样本量条件下，弹着点相对于各诱饵的生存概率分布规律。

通过挂飞试验，根据飞行试验数据和导弹的飞行规律能够推算每次飞行时反辐射导弹的弹着点位置。对应多次飞行试验结果，估计弹着点在坐标轴X、Y方向的均值为μx、μy，标准差为σx、σy，相关系数为r等参数，计算公式为：

(3)

(4)

(5)

(6)

(7)

式中，xi、yi为第i次试验中弹着点在X、Y方向的坐标。由上述参数可以得到弹着点服从正态分布的概率密度函数为：

f(x,y)=(2πσxσy(1-r2)1/2)-1·

exp(-(2(1-r2))((x-μx)2/σx2-

(8)

根据概率密度函数，分别对被保护雷达及三辆诱饵车在半径为R的圆形安全区域内进行积分，得到导弹击中该辐射源的概率，即能够得到导弹攻击时各辐射源的生存概率P为：

P=1-∬f(x,y)dxdy

(9)

2.3　多样本群条件下的数据处理方法

通常，试验中根据不同试验态势可获得多个子样本群数据[8]。如挂飞试验中，可以根据反辐射导弹来袭方向，选择不同的攻击角度，考核诱饵在360°空域范围内的诱偏能力，此时将每个攻击角度所进行的若干次试验作为一个子样本群，多个攻击角度的试验结果即为多个子样本群。因此，实际处理时，不论是二点分布参数估计，还是基于正态分布概率密度函数的统计方法，针对子样本群均可采用下面2种方法进行处理。

1)子样本群加权处理

以每个子样本群为基础，分别计算各个子样本群的生存概率，之后再对各个子样本群的计算结果进行加权处理。若有3个子样本群，则某辐射源的生存概率P为：

P=k1P(A)+k2P(B)+k3P(C)

(10)

式中，P(A)、P(B)、P(C)分别为各子样本群的生存概率，k1、k2、k3分别为各个子样本群的权系数。权系数的确定可根据该样本群在试验结果中所占有的重要程度进行设定。

2)样本群综合处理

将各个子样本群的结果综合为一个统一的样本群，再统计各个辐射源的生存概率。

上述2种统计结果处理方法均基于诱偏环境下反辐射导弹弹着点分布服从正态分布的假设，该统计方法相较于比例统计方法能够体现弹着点分布规律、部分消除试验过程的随机性，一定程度上优化了生存概率统计方法。

3　生存概率统计的图表显示方法

为了定量评估被试装备在反辐射导弹来袭过程中的诱饵及被保护雷达的生存概率，可采用反辐射导引头外场挂飞的试验方法，动态模拟反辐射导弹攻击过程，得出反辐射导弹的弹着点和命中被保护雷达及各诱饵的次数，统计被保护雷达及各诱饵的生存概率。

假设，某诱饵生存概率设计指标为92%，试验中选取3个攻击方向进行飞行试验，且每个攻击方向按照置信水平80%、允许抽样误差±10%确定子样本群的样本量，即在每个攻击方向需至少进行15次试验。在攻击方向为θ1时，进行的15次试验中，3个诱饵各被击中1次；在攻击方向为θ2时，进行的15次试验中，诱饵1被击中1次、诱饵2被击中2次、诱饵3未被击中；在攻击方向为θ3时，进行的15次试验中，诱饵1未被击中、诱饵2被击中1次、诱饵3被击中1次。

下面采用上述方法，分别对诱饵的生存概率进行统计。

3.1　基于二点分布参数估计的统计结果显示

1)子样本群加权处理

飞行试验中，不同攻击方向的弹着点分布如图1所示。

图1中，攻击方向为θ1时，3个诱饵的生存概率均为93.33%；攻击方向为θ2时，诱饵1、诱饵2、诱饵3的生存概率分别为93.33%、86.67%、100%；攻击方向为θ3时，诱饵1、诱饵2、诱饵3的生存概率分别为100%、93.33%、93.33%。

假设反辐射武器从θ1方向进行攻击的概率为40%，而从θ2、θ3方向进行攻击的概率均为30%，统计3个子样本群的最终结果时需进行加权处理，加权系数分别为0.4、0.3、0.3，则诱饵1、诱饵2、诱饵3的生存概率分别为95.33%、91.33%、95.33%。

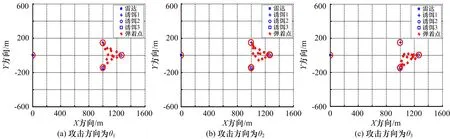
图1　基于二点分布参数估计的弹着点分布示意图

2)子样本群综合处理

将上述3个攻击方向的试验结果作为1个整体样本群进行统计处理，也可以将其看作是3个子样本群进行等加权处理的特殊情况，此时共飞行45个有效航次，弹着点分布如图2所示。此时，诱饵1、诱饵2、诱饵3的生存概率分别为95.56%、91.1%、95.56%。

3.2　基于正态分布概率密度函数的统计结果

1)子样本群等加权处理结果

与二点分布参数估计统计结果相对应，不同攻击方向时，其概率密度函数在4个辐射源所在位置的分布如图3所示。

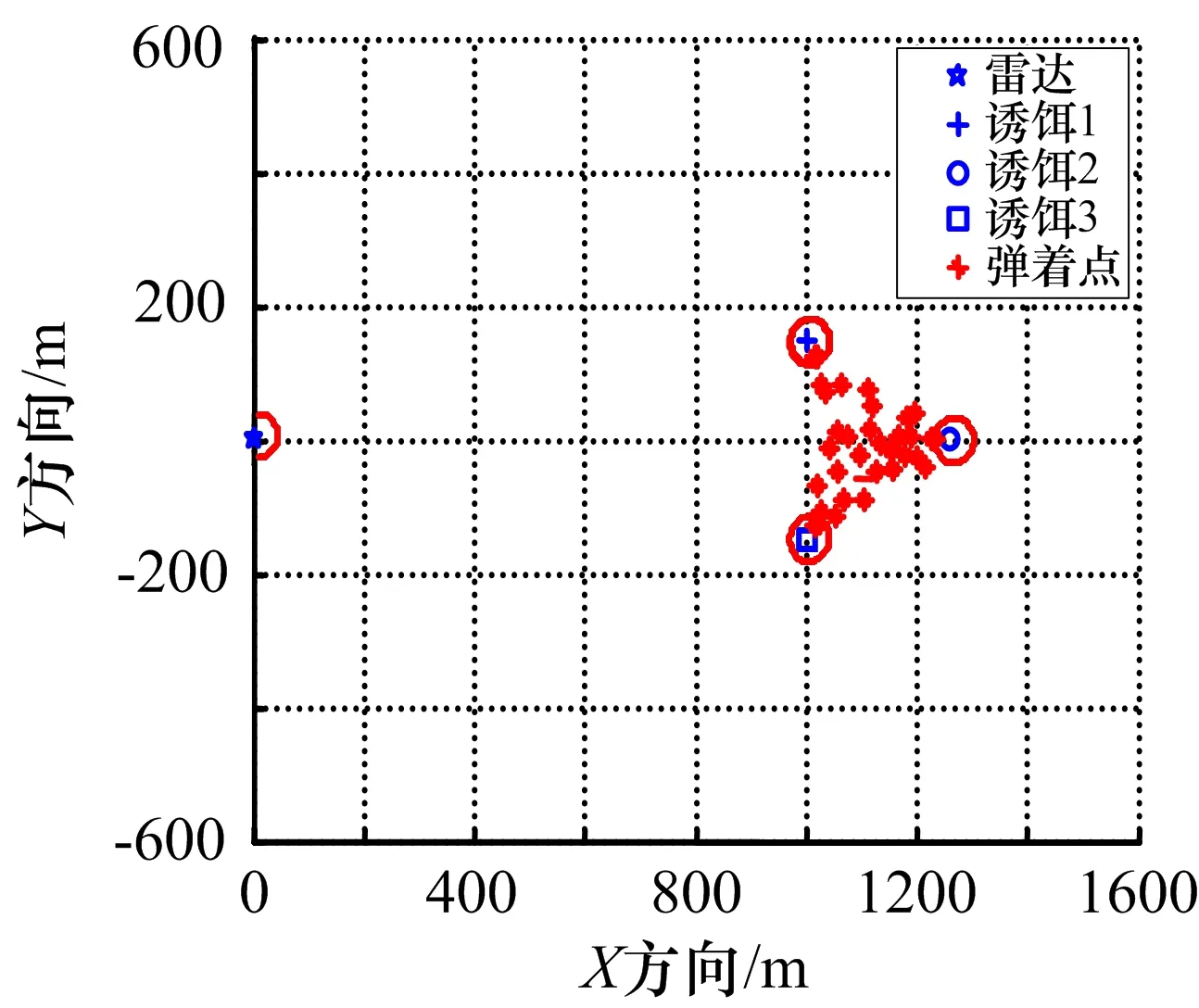
图2　基于二点分布参数估计的弹着点分布示意图

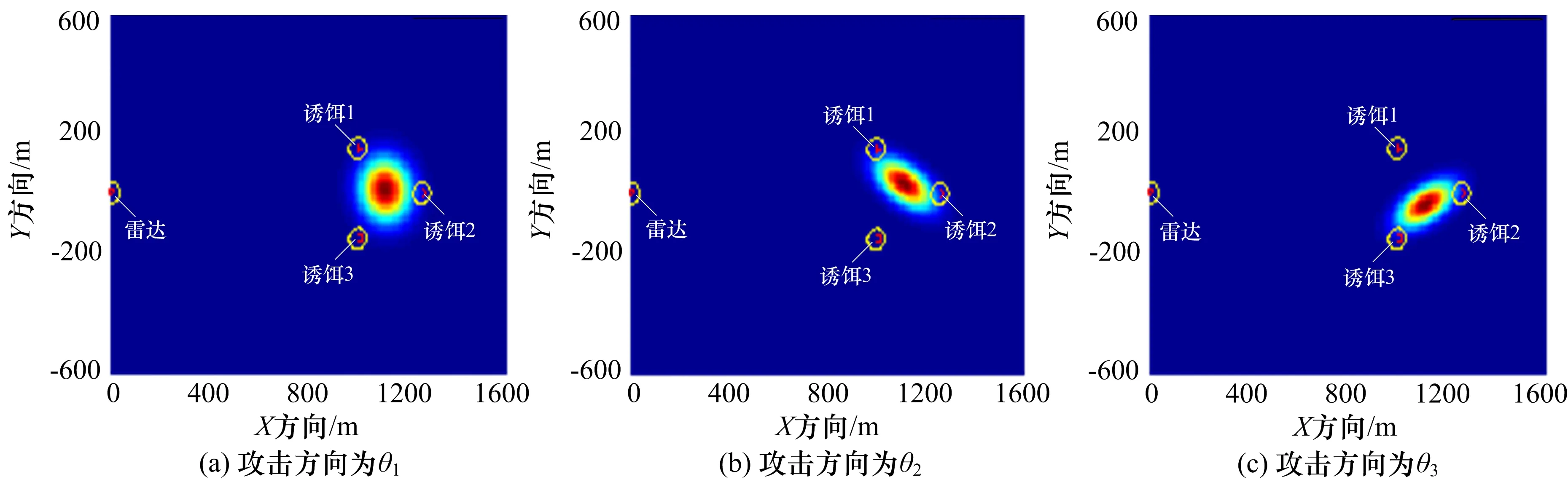
图3　概率密度函数分布图

根据概率密度分布结果可得，攻击方向为θ1时，诱饵1、诱饵2、诱饵3的生存概率分别为99.44%、98.88%、99.71%；攻击方向为θ2时，诱饵1、诱饵2、诱饵3的生存概率分别为98.49%、97.87%、100%；攻击方向为θ3时，诱饵1、诱饵2、诱饵3的生存概率分别为100%、97.55%、98.2%。

假设反辐射武器从θ1方向进行攻击的概率为40%，而从θ2、θ3方向进行攻击的概率均为30%，统计3个子样本群的最终结果时需进行加权处理，加权系数分别为0.4、0.3、0.3，则诱饵1、诱饵2、诱饵3的生存概率分别为99.31%、98.10%、99.30%。

2)子样本群综合处理结果

综合考虑3个攻击方向的弹着点分布情况，将3个方向的弹着点作为一个样本群进行综合处理。落点的分布情况如图2所示，其概率密度函数在4个辐射源所在位置的分布如图4所示。

计算得到被保护雷达、诱饵1、诱饵2、诱饵3的生存概率分别为：99.68%、98.52%、99.71%。

3.3　生存概率统计结果比较

综合对比4种生存概率统计方法，结果如表1所示。

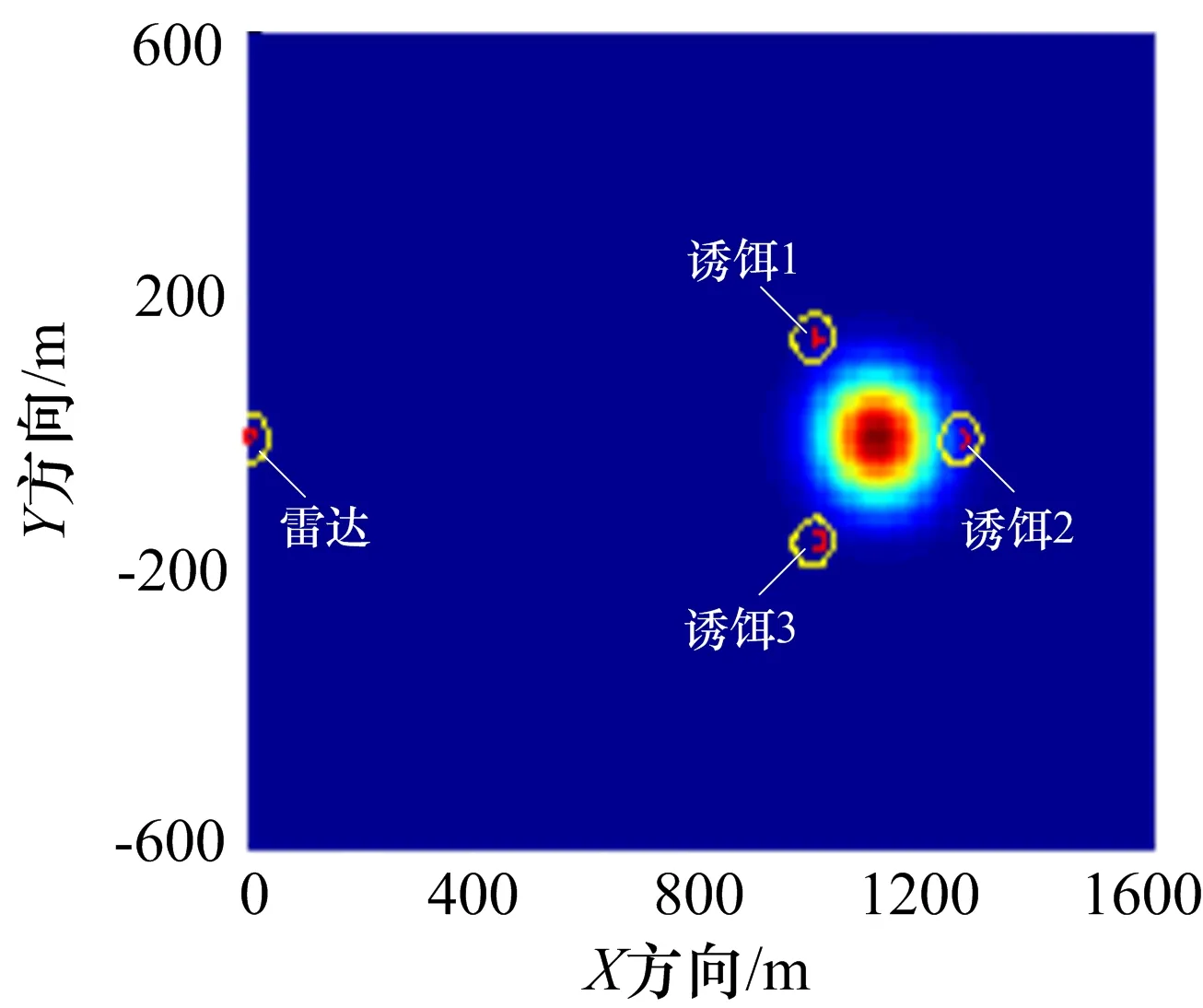
图4　概率密度函数分布图

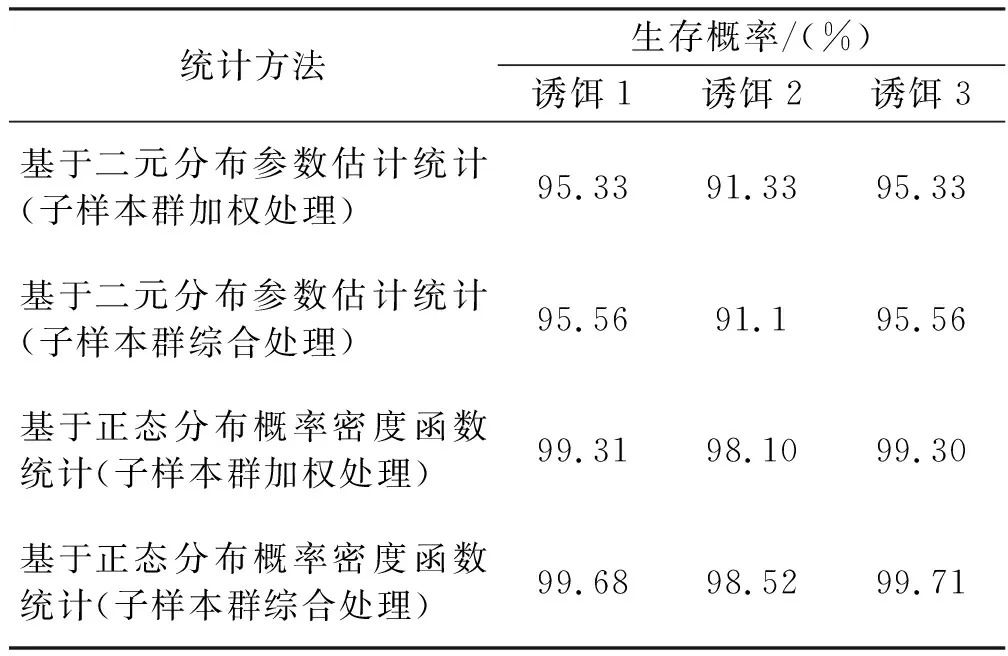
统计方法生存概率/(%)诱饵1诱饵2诱饵3基于二元分布参数估计统计(子样本群加权处理)95.3391.3395.33基于二元分布参数估计统计(子样本群综合处理)95.5691.195.56基于正态分布概率密度函数统计(子样本群加权处理)99.3198.1099.30基于正态分布概率密度函数统计(子样本群综合处理)99.6898.5299.71

由结果可以看出，在样本量有限的情况下，基于二点分布参数估计的统计方法，由于单次试验结果的偶然性，统计得出各诱饵的生存概率之间的变化较大。而基于正态分布概率密度函数统计方法，通过确定弹着点的概率密度函数，可以得出相对精确的生存概率统计结果，但是如果样本量有限，弹着点分布就不严格服从正态分布，因此该统计方法还有可改进之处。

4　结束语

本文中的2种统计结果处理方法，均基于诱偏环境下反辐射导弹弹着点分布服从正态分布的假设，但是，基于正态分布概率密度函数统计统计方法相较于基于二元分布参数估计统计方法，更能够体现弹着点分布规律、部分消除试验过程的随机性，一定程度上优化了生存概率统计方法。需要注意的是不管采用何种方法，如要获得准确度更高的生存概率统计，就必须采取更大的样本量。相较而言，基于正态分布概率密度函数的统计方法能够利用有限的样本量数据反映反辐射武器的弹着点分布规律，能够更直观地获得各辐射源的生存概率分布规律。■