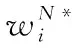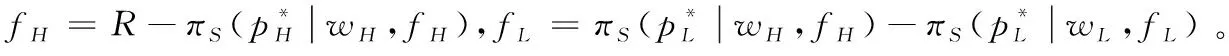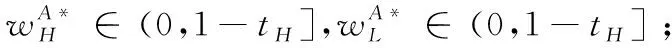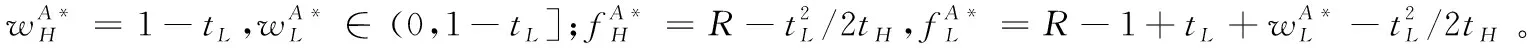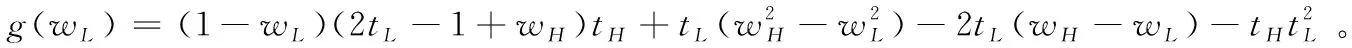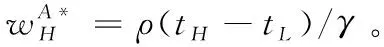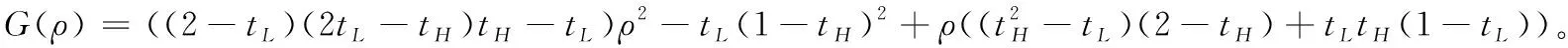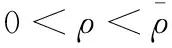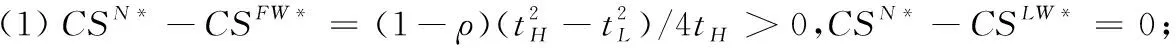不对称信息下“农超对接”供应链定价及合同设计
2018-07-13金亮
金 亮
(1.南昌大学中国中部经济社会发展研究中心,江西 南昌 330031;2.南昌大学经济管理学院,江西 南昌 330031)
1 引言
自2008年以来,商务部和农业部联合下发了多个文件推动“农超对接”试点工作的部署,并向全国进行推广[1],如《关于开展农超对接试点工作的通知》[2]、《商务部、农业部关于全面推进农超对接工作的指导意见》[3]等。“农超对接”模式能够减少农产品流通环节,提高流通效率,增加农户收入并降低超市销售成本[4-5],有助于缓解农民农产品“卖难”和消费者“买贵”同时存在的矛盾[6]。然而,在“农超对接”模式中,由于超市直接面对消费者,往往拥有更多的市场信息,这使得远离市场的农户决策问题变得复杂,并有可能导致农户无法获得公平的合作收益。并且,容易发现,由于农产品生产周期长、技术结构复杂、技术改进较为困难等特点,使得农户在生产过程中难以提高农产品的数量和质量,这进一步加大了“农超对接”模式中超市与农户的合作难度,并有可能导致农产品“卖难买贵”现象的发生。面对这些问题,本文基于农户与超市在“农超对接”模式中的博弈关系分析,旨在研究不对称的市场信息会对“农超对接”模式造成何种影响?“农超对接”模式是否能够有效缓解农产品“卖难”和“买贵”的矛盾?超市是否愿意与农户共享市场信息等一系列问题。
近十年来,农产品供应链管理得到国内外学者的广泛关注[7-9]。Cai Xiaoqiang等[10]考虑了生鲜农产品在运输过程中存在的数量与质量损耗,构建了努力水平影响损耗的两阶段供应链优化模型;凌六一等[11]考虑了农产品产出和以农产品为原料的加工产品需求均为随机的情形,研究了不同风险分担契约对供应链均衡的影响;Cai Xiaoqiang等[12]针对由一个生鲜农产品供应商、一个销售商和一个第三方物流服务提供商组成的生鲜农产品供应链,考虑物流外包对农产品新鲜度的影响,研究了农产品新鲜度影响需求下的供应链成员最优决策和协调契约设计问题;Wu Qing等[13]同样针对生鲜农产品物流外包问题,研究了分销商与第三方物流服务提供商之间的不同权力结构对物流服务质量的影响,并设计了相应的协调契约;Hu Hongtao等[14]则从成本视角,构建了混合整数规划模型来研究如何降低生鲜农产品的物流成本;张伟和周根贵[15]研究了生鲜农产品供应链订货问题;李琳和范体军[16]对比分析了农产品零售商在固定定价、动态定价以及带有降价时点考虑的定价等三种不同定价模式下最优定价与订货决策;Chang Xue等[17]研究了考虑消费者偏好下的农产品定价问题;Tang等[18]研究了部分价格保证策略对农户和农产品销售企业最优决策及利润的影响;Nakandala等[19]针对农产品易腐和短生命周期特点,构建了生鲜农产品供应链风险评估模型,并用案例对其有效性进行了检验。上述关于农产品供应链管理的文献均基于完全信息背景,仅杨亚等[20]考虑了信息不对称因素,但其研究的是农产品新鲜度信息不对称下的供应链协调问题。与已有研究不同的是,本文考虑市场信息不对称,研究“农超对接”模式下农户与超市合同设计问题。
另外一个与本文相关的问题是关于“农超对接”模式的研究,已有研究主要聚焦于“农超对接”模式的价值分析。Hu Dinghuan等[4]认为“农超对接”模式可以有效解决农产品流通环节过多及成本过高问题,有利于提高农户收益并降低农产品市场销售价格;王志刚等[21]基于蔬菜产销合作社调查数据,发现了“农超对接”模式有助于降低农产品的流通成本;浦徐进等[22]对比分析了不同“农超对接”模式下的农户生产努力投入、超市销售努力投入以及农产品供应链效用水平;李崇光等[23]对比分析了大型批发市场流通模式、地头市场流通模式以及“农超对接”流通模式等三种流通模式下的蔬菜价格,发现“农超对接”流通模式能够有效降低农、超双方的交易成本,缓解蔬菜价格波动;Niu Baozhuang等[24]分别针对“农户+企业”模式和“农户+合作社+企业”模式,分析了批发价格契约和成本共担契约对农产品供应链成员效用的影响;浦徐进和金德龙[25]针对“农超对接”模式,研究了生鲜农产品社区直销店的开设对合作社和超市最优决策的影响,发现开设社区直销店有助于提高合作社的利润水平,并在一定条件下有利于改善“农超对接”模式下生鲜农产品供应链的运作效率。上述文献比较了“农超对接”模式与其他农产品流通模式的差异,研究了“农超对接”模式的价值。不同的是,本文从信息不对称下的机制设计视角,研究“农超对接”模式下农产品供应链定价及合同设计问题。
鉴于此,本文以由一个农户和一个超市组成的“农超对接”系统为研究对象,考虑我国农户农产品生产的特点,以及市场上消费者对农产品质量偏好的异质性,研究“农超对接”模式下农产品供应链定价及合同设计问题。在此“农超对接”模式中,农户需要决策的问题是如何确定农产品的批发价格合同并保证超市愿意参与合作,以最大化自身利润;而超市则要根据农户给定的合同,确定农产品的销售价格。本文依据消费者效用理论,分别研究信息对称与不对称下的农户策略性批发合同设计和超市农产品定价策略;进而考察消费者偏好与农产品质量不匹配信息对农产品价格、销售量(滞销量)以及消费者剩余的影响,分析农户与超市如何通过谈判实现信息共享。
2 问题描述
考虑由一个农户(F)和一个超市(S)组成的“农超对接”系统中,农户生产的一种农产品通过超市销往市场。假设农户生产的农产品产量与质量是确定的,这主要有两方面的原因:一是农业生产的滞后性和长周期性,农户很难改变生产计划;二是我国农户生产规模往往比较小,并不能够进行有效的技术投入[5-6]。因此,不失一般性,假定农户生产的农产品产量为1。
考虑农户生产的农产品质量是确定的,其颜色、大小、形状等可能会与消费者偏好存在一定的偏差,因而当消费者在购买农产品时,会发生不匹配成本[26]。并且,考虑现实中消费者的异质性,不同的消费者对农产品质量往往具有不同的偏好,故依据文献[27-28],假定消费者均匀分布在长度为2n的直线上,密度为1,农产品质量位于中点1/2处,则消费者与中点1/2处的距离可以表示为消费者购买农产品的不匹配成本,如图1所示。由此,得到位于x(x~U[-n,n])处的消费者不匹配成本为t|1/2-x|,其中t为单位不匹配成本。

图1 消费者效用示意图
可以得到消费者购买农产品获得的净效用为
(1)
其中,p为由超市确定的农产品销售价格;为简化模型表达,假设消费者对农产品的支付意愿为1。
用(A,B)+表示max{A,B},(A,B)-表示min{A,B}。设a=((1-p)/t,0)+,表示当消费者愿意购买农产品时,消费者在直线上位置允许偏离1/2处的最大值。由此,得到农产品的销售量为:
(2)
由于超市直接面对消费者,故超市拥有关于消费者不匹配成本的私有信息,而远离市场的农户则无法准确知道消费者不匹配成本信息。假设消费者不匹配成本存在两种可能,分别用tL和tH来表示(tL/tH<1),其中tL为低成本类型(低类型;L),tH为高成本类型(高类型;H)。并且,消费者不匹配成本为低(高)类型的概率为ρ(1-ρ),0<ρ<1,这是农户和超市的公共知识。为此,农户根据消费者不匹配成本的类型i(i=LorH)设计两种类型的合同{wH,fH}和{wL,fL},供超市选择,其中与Cai等[10]的研究类似,由农户确定农产品批发价格wi,fi为农户支付给超市的一次性转移支付,这是因为在“农超对接”模式中,农户普遍处于弱势地位,而掌握销售渠道的超市处于强势地位,农户需要向超市支付fi,以满足超市盈利需求[23]。特别地,若fi=0,则表示农户不用向超市支付额外费用。
依据上述模型假设,在给定{w,f}下,超市的利润为
πS(p|w,f)=(p-w)q(p)+f
(3)
考虑我国农户农产品生产规模往往较小,且缺乏技术投资等原因[5],假设其边际生产成本为常量,因不影响结果分析,故标准化为零。农户的利润为
πF(w,f)=wq(p)-f
(4)
供应链系统的利润为
πSC(p)=pq(p)
(5)
3 模型分析
采用逆向归纳法,先分析超市的农产品定价策略,然后再分析农户的批发价格合同设计。
3.1 超市的最优定价策略
当消费者为i(i=LorH)类型时,给定合同{wi,fi},超市以自身利润最大化为目标决策农产品销售价格。得到优化问题:
(6)
采用Kuhn-Tucker方法求解上述问题(6),可得唯一最优解。
引理1 当消费者为i(i=LorH)类型时,给定合同{wi,fi},超市的最优定价策略为
(7)
证明:见附录。
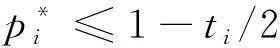
3.2 对称信息下的最优合同设计
对称信息下,农户知道消费者类型为i(i=LorH),并设计批发合同{wi,fi}。此时,农户需要解决如下优化问题。本文用字符“N”表示“对称信息”。
(8)
问题(8)中,约束式(IR)为个体理性约束,本文假设农户知道超市的保留利润为R,并且R≤1-tL/2,否则农户不会参与合作。那么,约束式(IR)表示超市获得的利润不能小于其保留利润,即说明超市一定会接受农户的合同。
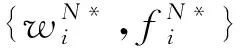
(9)
证明:见附录。
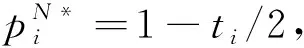
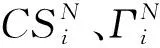
(10)
(11)
证明:见附录。
命题1表明,在“农超对接”模式下,若消费者不匹配成本为对称信息,则农户通过“批发价格+一次性转移支付”的合同设计能够实现农产品供应链的完美协调。还可以发现,随着消费者不匹配成本的变化,超市通过调整农产品的销售价格,总是能够使农户生产的农产品全部售出,而不会滞销。此时,由于消费者剩余还受到农产品销售价格的影响,因而消费者剩余反而会降低,但对供应链系统利润和社会福利总是有利。
3.3 不对称信息下的最优合同设计
对称信息是理想情形。现实中,消费者的不匹配成本信息并不能被农户完全准确观测到,因而在不对称信息下,农户在设计合同时还需甄别消费者类型。此时,农户面临如下优化问题。本文用字符“A”表示“不对称信息”。
(12)
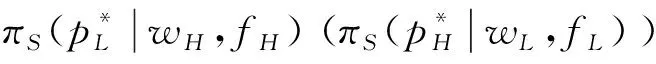
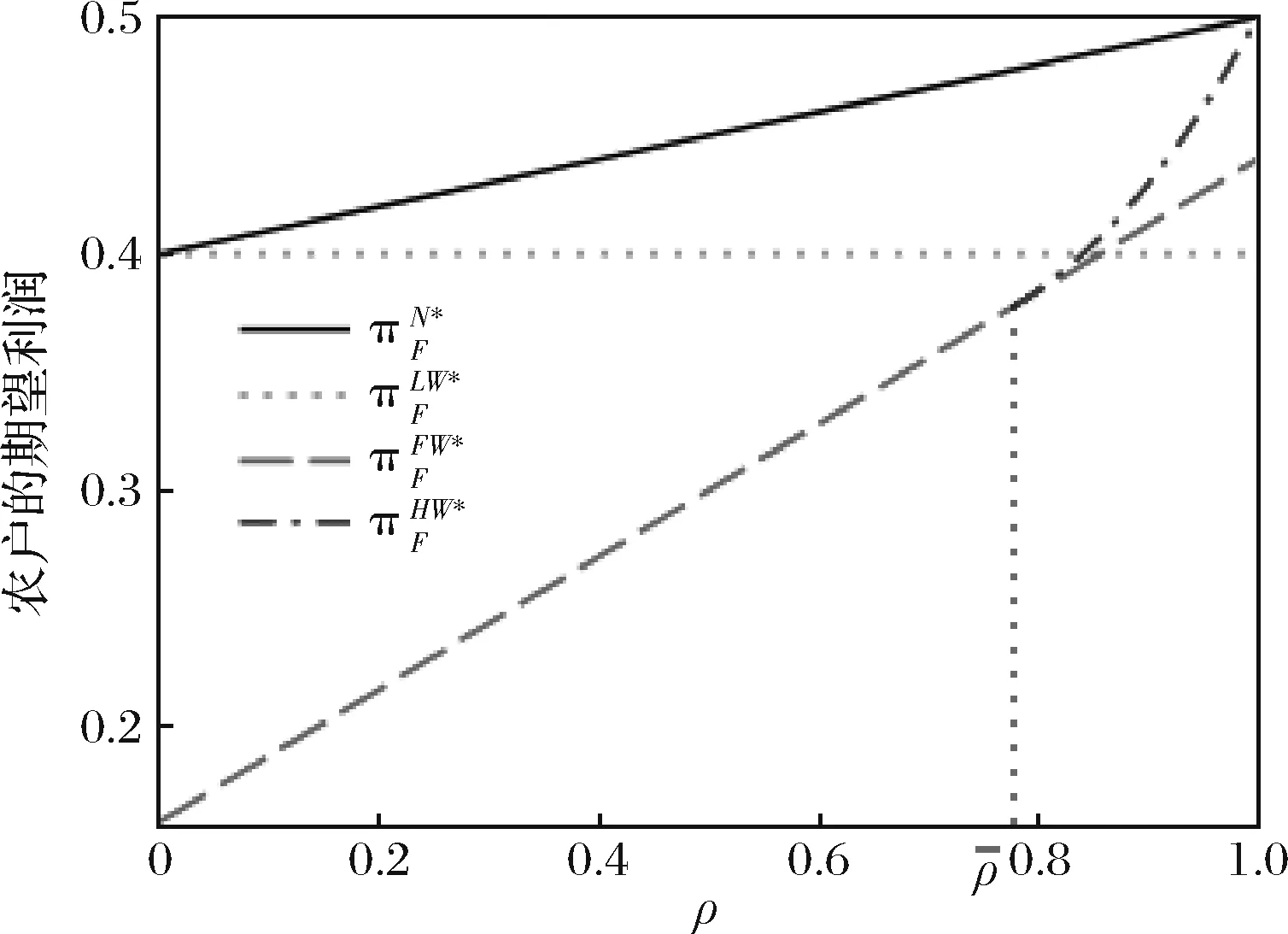
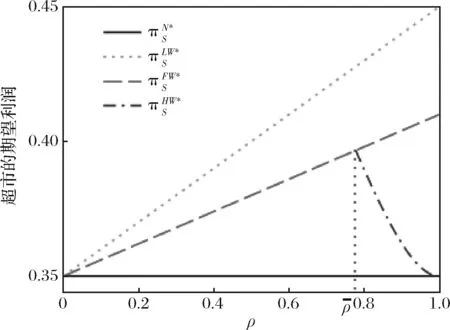
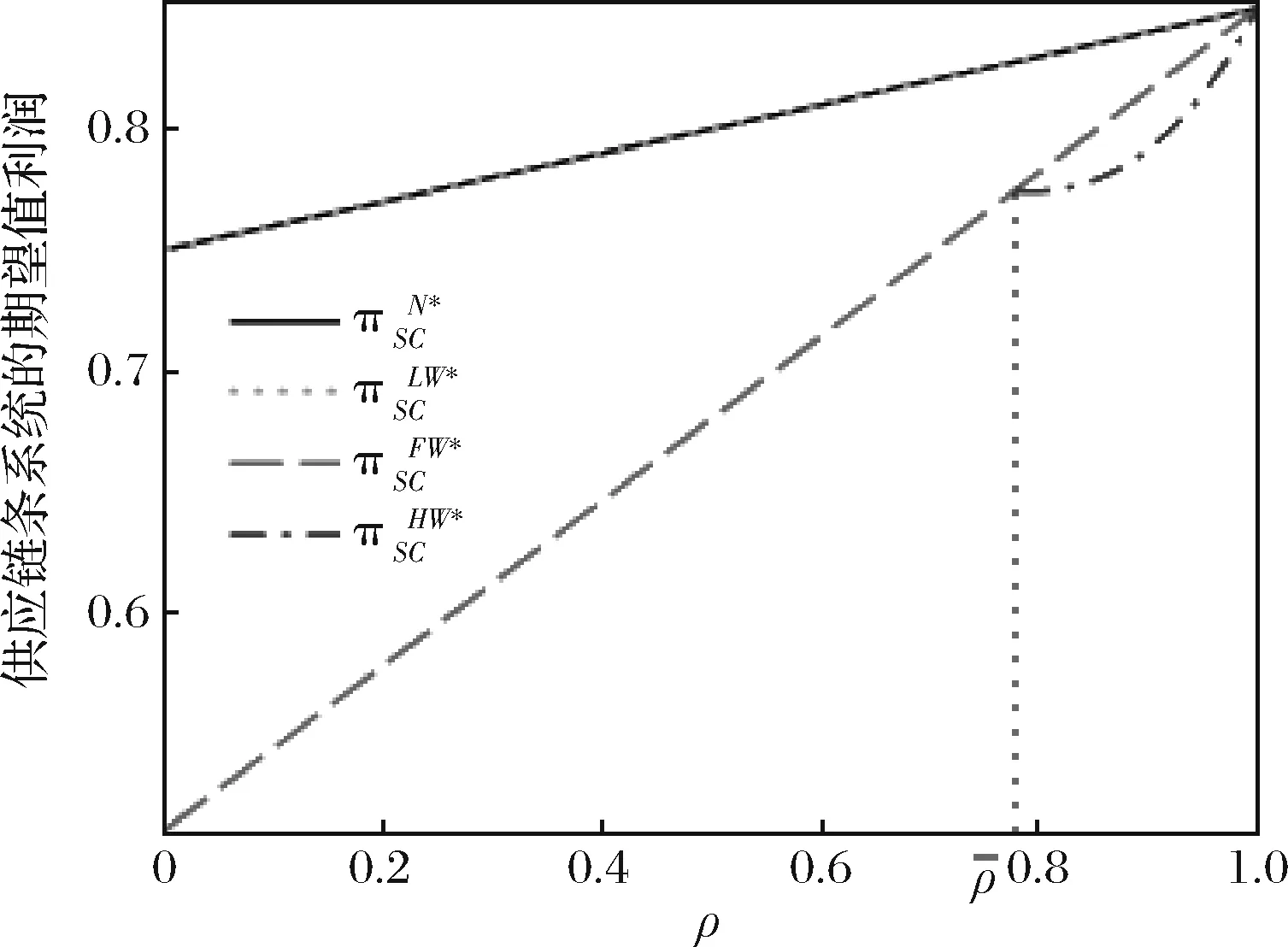
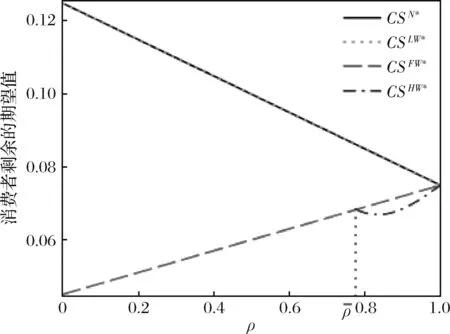
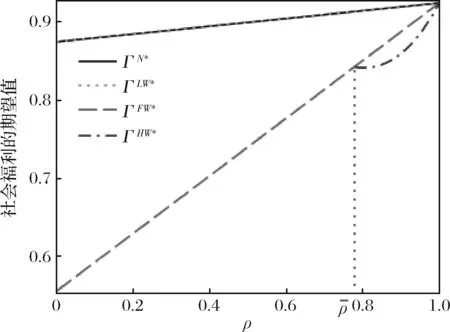
根据引理1,农户的批发价格决策存在两个临界值1-tH和1-tL。为简化表达,依据批发价格wH的大小,定义:① 当wH≤1-tH时,农户的合同设计{wi,fi}(i=LorH)称为“低价策略”,用字符“LW”表示;② 当wH=1-tL,农户的合同设计{wi,fi}称为“固定价格策略”,用字符“FW”表示;③ 当1-tL 证明:见附录。 表1 不对称信息下的农户最优合同设计 推论1 在LW策略下,农产品不会滞销;而在FW和HW策略下,仅当消费者为H类型时,农产品才会滞销。 证明略。 推论1表明,在不对称信息下,农户设计的合同有可能导致农产品滞销。当消费者为L类型时,农户较低的批发价格会诱使超市设置较低的农产品销售价格,此时农户生产的农产品将全部销售完。当消费者为H类型时,农户生产的农产品有可能滞销。具体分析,在LW策略下,农户设置的批发价格较低,因而农产品销售价格也较低,农产品会全部销售完;但在FW和HW策略下,较高的批发价格会使超市设置较高的农产品销售价格,导致部分农产品滞销。 命题2 比较三种不同批发价格策略下的农户期望利润,可以得到: 证明:见附录。 图2 ΔLF、ΔLH、ΔFH随ρ变化 ρ∈(0,ρLH) (13) 容易发现,LW策略的可行条件取决于两种类型消费者的不匹配成本。由∂ρLH/∂tL>0可知,L类型消费者的不匹配成本tL越大,可行性越有可能提高;由∂ρLH/∂tH<0可知,H类型消费者的不匹配成本tH越大,可行性越有可能降低。依据推论1,还可以知道,当农户选择LW策略时,农产品销售价格较低,农产品不会滞销。但是,当农户选择HW策略时,农产品销售价格较高(消费者“买贵”),农产品会滞销(农户“卖难”)。进一步分析农产品滞销与农户期望利润之间的关系,得到推论2。 推论2 在FW和HW策略下,农户农产品有可能滞销,但并不一定会造成农户期望利润损失。 证明略。 推论2表明,农产品滞销并不一定意味着农户期望利润会产生损失。在LW策略下,农户生产的农产品总是能够销售完,若满足条件ρ∈(0,ρLH),则农户选择LW策略获得的期望利润要高于其他策略下的值,表明农产品不滞销总是有利于农户。但在FW和HW策略下,当消费者为H类型时,农产品会滞销,此时若满足ρ∈(ρLH,ρLF),则农户的最优选择为HW策略,且LW策略优于FW策略,表明农产品是否滞销与农户获得期望利润的大小并无直接关系;若满足获得ρ∈(ρLF,1),则农户的最优选择仍为HW策略,且FW策略优于LW策略,表明此时农产品滞销反而对农户有利。 推论3 比较不同批发价格策略下的消费者剩余和社会福利期望值,可以得到: (1)CSLW*>CSFW*>CSHW*; (2)ΓLW*>ΓFW*>ΓHW*。 证明:见附录。 由推论3可知,当ρ∈(ρLH, 1)时,农户以自身期望利润最大化为目标选择HW策略,这将导致超市和供应链系统期望利润的损失。因此,进一步考察超市是否可以通过给予农户适当的补贴,使农户选择LW策略,得到命题3。 证明:见附录。 命题3表明,当农户选择HW策略时,超市可以通过给予农户一定的补贴,且当补贴额度满足一定条件时,农户将会选择LW策略。依据命题2,当ρ∈(ρLH,1)时,HW策略下农户能够获得高于其他两种策略下的期望利润,但此时超市的期望利润较低。因此,超市可以通过给予农户一定的补贴,并使农户获得补贴后的期望利润不低于LW策略下的值,由此激励农户选择LW策略,此时农户与超市获得的期望利润均增加,实现“共赢”。此外,容易知道,当超市通过补贴使农户选择LW策略时,农产品将不会滞销,消费者剩余和社会福利均能得到有效提升。 本节首先分析不对称信息对农户、超市以及供应链系统期望利润的影响;然后,考察不对称信息对消费者剩余和社会福利期望值的影响。 依据定理1和定理2,比较信息对称与不对称下的超市最优定价策略,得到命题4。 证明:见附录。 推论4 农产品滞销量受到如下因素的影响: 证明略。 推论4表明,在FW和HW策略下,当H类型消费者的不匹配成本较高时,农产品滞销量也较高。并且,也容易发现,在FW策略下,消费者为H类型的概率或市场上H类型的消费者数量并不会影响农产品滞销量;而在HW策略下,当消费者为H类型的概率较大时,反而有利于降低农产品的滞销量。 命题5 农户信息价值、超市信息租金以及供应链损失见下表2。 证明:依据定理1和定理2,比较对称信息和不对称信息下的农户、超市以及供应链系统的期望利润,即可得,略。 表2 农户信息价值、超市信息租金以及供应链损失 其中,g1(ρ)=tL(1-ρ)(1-tH)2-ρtH(2-tH)(tH-tL), g2(ρ)=(1-ρ)((1-ρ)(1-tH)tL+ρ(2-tH)(tH-tL))((1-ρ))(1-tH)tL-ρtH(tH-tL))。 依据表2,容易知道,在LW策略下,农户的信息价值与超市的信息租金相等(ΔπF=ΔπS),因而不对称信息的存在并不会给供应链系统造成损失(ΔπSC=0),这可以看作农户给予超市的“信息共享费”,以激励其披露私有的市场信息,从而使得“农超对接”模式下的农产品供应链系统利润达到最优水平;在FW和HW策略下,农户信息价值要大于超市获得的信息租金(ΔπF>ΔπS),故不对称信息的存在会导致供应链系统利润损失。该命题表明,在“农超对接”模式下,不对称信息的存在不一定会造成供应链损失,即当且仅当农户选择LW策略时,不对称信息的存在仅导致利润份额在供应链系统内部的重新分配。 推论5 农户信息价值、超市信息租金与供应链损失三者之间存在关系:ΔπF=ΔπSC+ΔπS。 证明略。 由推论5可知,农户信息价值同时包含了超市信息租金和供应链损失。在LW策略下,超市的最优定价决策等于对称信息下的值,供应链损失为0,ΔπF=ΔπS;在FW和HW策略下,超市的最优定价决策会偏离对称信息下的值,造成供应链损失,ΔπF=ΔπSC+ΔπS。该推论表明,在不对称信息下,农户在设计合同时,可以通过权衡超市信息租金与供应链损失,以最小化自身信息价值,从而实现自身期望利润最大化。 在“农超对接”模式下,考虑我国农户在与超市合作过程中,掌握销售渠道的超市往往拥有正的谈判力,并假设超市的谈判力为α,则农户的谈判力为1-α。不考虑农户与超市的谈判成本,得到命题6。 为简化表达,先设定以下2个阈值: 证明:见附录。 本节将分析不对称信息的存在对消费者剩余和社会福利的影响。 命题7 比较信息对称与不对称下的消费者剩余和社会福利的期望值,可以得到: (1)CSLW*=CSN*,CSHW* (2)ΓLW*=ΓN*,ΓHW*<ΓFW*<ΓN*。 证明:见附录。 由命题7可知,在LW策略下,无论消费者为何种类型,农产品总是不会滞销,消费者剩余和社会福利不会发生变化,因而在不对称信息下,消费者剩余和社会福利的期望值均能达到最优水平(对称信息下的值);在FW和HW策略下,当消费者为H类型时,农产品滞销,消费者剩余和社会福利均降低,即不对称信息的存在会导致消费者剩余和社会福利的损失。并且,还可以知道,FW策略下的消费者剩余和社会福利均要高于HW策略下的值。该命题表明,不对称信息的存在并不一定会导致消费者剩余和社会福利的损失,仅当农产品未滞销时,消费者剩余和社会福利才能达到最优水平。 推论6 当超市与农户达成谈判时,消费者剩余和社会福利的期望值均能达到最优水平(对称信息下的值)。 证明略。 推论6表明,当农户选择HW策略时,若超市的谈判力能够使其与农户达成信息共享谈判,则农户将会选择LW策略,此时消费者剩余和社会福利的期望值均能达到对称信息下的值。并且,容易知道,超市的谈判力并不会对消费者剩余和社会福利产生影响。 下面将通过数值算例直观考察上述理论分析结果,设置参数:tH=0.5,tL=0.3,R=0.35,以ρ为横坐标,分别绘制对称信息与不对称信息下的供应链成员及供应链系统期望利润、消费者剩余及社会福利期望值的影响曲线。 图3 ρ对农户期望利润的影响曲线 图4 ρ对超市期望利润的影响曲线 图5 ρ对供应链系统期望利润的影响曲线 图6 ρ对消费者剩余期望值的影响曲线 图7 ρ对社会福利期望值的影响曲线 观察图6和图7可以发现:(1) 在LW策略下,不对称信息下的消费者剩余和社会福利期望值均能达到对称信息下的最优水平(CSLW*=CSN*、ΓLW*=ΓN*),表明当农户选择LW策略时,供应链成员之间的信息不对称并不会影响消费者剩余和社会福利;(2) 在FW和HW策略下,不对称信息下的消费者剩余和社会福利期望值均低于对称信息下的值,表明当农户选择FW或者HW策略时,不对称信息的存在会导致消费者剩余和社会福利的损失;(3) 在FW和HW策略下,不对称信息给消费者剩余和社会福利造成的损失总是会随ρ的增大而减小,表明较大的ρ有利于缓解不对称信息给消费者剩余和社会福利带来的不利损失;(4) 比较FW和HW策略下的消费者剩余和社会福利,容易知道,FW策略下的消费者剩余和社会福利总是要高于HW策略下的值。 本文针对由一个农户和一个超市组成的“农超对接”系统,考虑农户生产的农产品在质量和数量方面不易改变的特点以及消费者偏好与农产品质量之间的不匹配成本为不对称信息,研究了超市的最优农产品定价策略以及农户最优合同设计问题。论文所得结论和启示可总结为以下4个方面: (1) 在对称信息下,农户通过调整农产品批发价格和一次性转移支付的大小,在保证超市会参与“农超对接”合作的前提下,可使超市设置合理的销售价格,使得农产品不会滞销。与集中式决策情形相比,此时供应链系统利润、消费者剩余以及社会福利均能达到集中式决策下的最优值,农户设计的合同能够实现“农超对接”模式下农产品供应链的完美协调。 (2) 在不对称信息下,农户的最优合同设计存在低批发价格策略、固定批发价格策略以及高批发价格策略等三种策略。当消费者不匹配成本为低类型的概率较低或市场上低类型的消费者数量较少时,农户会选择低批发价格策略,此时农产品不会滞销;否则,农户会选择高批发价格策略,此时农产品滞销,并导致消费者剩余和社会福利的损失。 (3) 不对称信息的存在会对农户和超市的最优决策造成影响,并导致农户期望利润的损失,超市能够获得额外的信息租金,但却不一定会给供应链系统造成损失。在低批发价格策略下,不对称信息的存在仅导致利润在供应链系统内部重新分配,此时农户与超市不能达成信息共享谈判;在高批发价格策略下,只要超市的谈判力满足一定条件,超市愿意披露其拥有的私有信息,从而与农户共享整个供应链的利润。 (4) 不对称信息的存在并不一定会影响消费者剩余和社会福利。在低批发价格策略下,消费者剩余和社会福利总是能够达到对称信息下的最优水平;在固定批发价格策略和高批发价格策略下,消费者剩余和社会福利均会低于对称信息下的值。特别地,在高批发价格策略下,当超市与农户达成信息共享谈判时,消费者剩余和社会福利均能够达到最优水平,且不受超市谈判力大小的影响。 本文研究的“农超对接”模式仅包含一个农户,现实生活中超市往往会与多个生产不同种类农产品的农户建立合作,因此,针对存在多个农户且各个农户生产不同种类农产品的“农超对接”模式,研究农产品定价及合同设计是未来可以进一步研究的方向。 附录:主要结论的证明 (1)引理1的证明: 依据式(2),分为(C1)和(C2)两种情形求解优化问题(6)。 (C1) 当(1-pi)/ti≥1/2时,q(pi)=1。易知,πS(pi)为关于pi的一次函数,故存在角点解,即存在唯一最优解。构建Lagrange函数: L(pi;λ)=πS(pi|wi,fi)+λ(1-ti/2-pi) (C2) 当(1-pi)/ti≤1/2时,q(pi)=2(1-pi)/ti。易知,πS(pi)为关于pi的凹函数,故存在内点解,即存在唯一最优解。构建Lagrange函数: (2)定理1的证明: 依据引理1,分为(C1)和(C2)两种情形求解优化问题(8)。 (C1) 当wi≤1-ti时,πF(wi,fi)=wi-fi。易知,在(IR)约束条件下存在角点解。构建Lagrange函数: 综合上述(C1)和(C2)两种情形,即可得到定理1。 (3)命题1的证明: 将农户和超市视为集中的决策主体,得到优化问题: (4)定理2的证明: (C1) 当wH≤1-tH,wL≤1-tH时,可以得到: πSL=R+(tH-tL)/2,ΔIC-H=0,πM=1-R-tH/2。 (C2) 当wH=1-tL,wL≤1-tH时,可以得到: 易知,πSL>R,ΔIC-H>0,即满足约束条件(IR-L)和(IC-H)。并且,πM>0为常量。 (C3) 当wH=1-tL,1-tH (C4) 当1-tL πSL=R+(tH-tL)(1-wH)2/2tLtH, ΔIC-H=(tH-tL)(tLtH-(1-wH)2)/2tLtH。 由πSL>R可知满足约束条件(IR-L),且ΔIC-H>0,故满足约束条件(IC-H)。 (C5) 当1-tL πSL=R+(tH-tL)(1-wH)2/2tLtH,ΔIC-H=f(wL)/2tLtH。 由πSL>R易知约束条件(IR-L)成立,同时可以验证即ΔIC-H≥0,即满足约束条件(IC-H)。 (6)命题2的证明: 比较三种不同批发价格策略下的农户期望利润,得到: (7)命题3的证明: (8)命题4的证明: (2)同理,在HW策略下,直接比较,易得,略。 (9)命题6的证明: (10)命题7的证明: 比较消费者剩余与社会福利的期望值,可以得到: (2)ΓN*-ΓFW*=(1-ρ)(tH-tL)(4-tH-tL)/4tH>0,ΓN*-ΓLW*=0;同样,由推论3可知,ΓFW*-ΓHW*>0。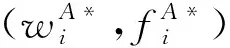
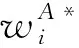

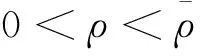
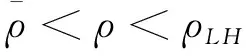
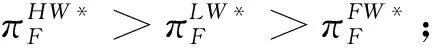
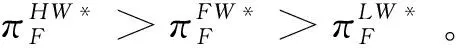
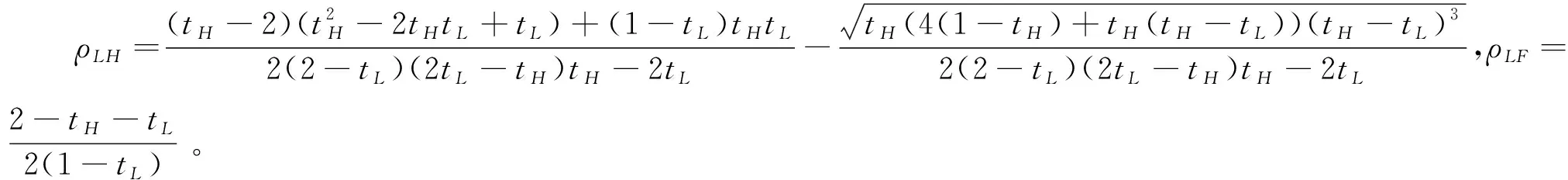
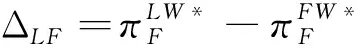

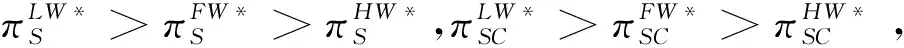
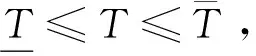
4 信息价值分析
4.1 不对称信息对农产品销售价格和销售量的影响

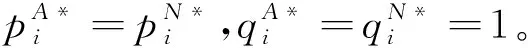
4.2 不对称信息对供应链成员和供应链系统的影响
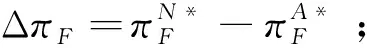
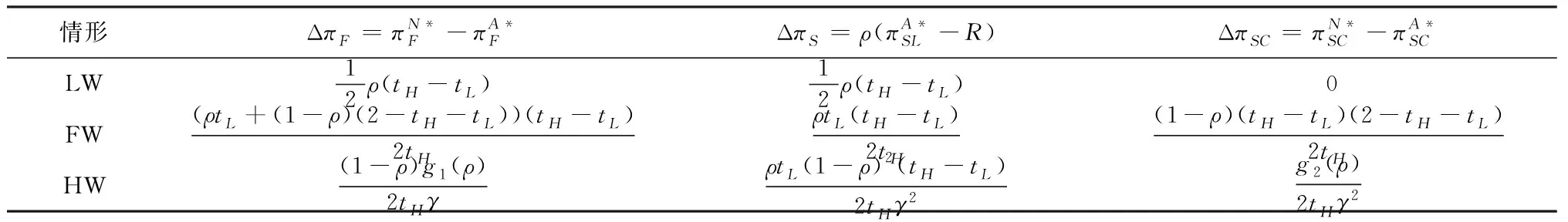

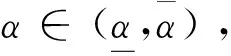

4.3 不对称信息对消费者剩余与社会福利的影响
5 算例分析
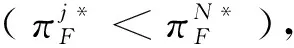

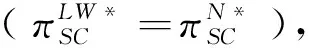
6 结语