基于高频数据的中国有色金属期货市场量价关系研究
2018-07-13朱学红张宏伟钟美瑞刘海波
朱学红,张宏伟,钟美瑞,刘海波
(1.中南大学商学院,湖南 长沙 410083; 2. 中南大学金属资源战略研究院,湖南 长沙 410083;3.康佳集团股份有限公司,广东 深圳 518000)
1 引言
成交量、持仓量与价格波动的关系一直以来受到学者的广泛关注,通过量价关系的研究不仅有助于加深对金融市场结构的理解,了解信息流如何进入市场,如何传播以及信息流入市场的方式和速度[1],而且能反映股票市场中的供求关系,判断和预测整个金融市场的走势[2]。期货市场上的价格波动是不易观察的隐性指标,而成交量、持仓量是易于观察的显性指标,交易者、套期保值者以及投机者可以通过观察成交量、持仓量的变化预测期货市场的价格波动,从而有效规避风险。同时量价关系的研究也可以使市场监管者和政策制定者更准确地评估市场的交易活动,为其进行有效的市场监管、趋势分析以及制定决策提供指导。因此围绕量(成交量和持仓量)与价(价格波动率)关系的研究具有重要的理论价值和实践意义。
围绕价格波动与成交量的关系,国内外进行了大量的研究。早在1973年,Clark[3]首次提出混合分布假说(MDH),将成交量作为信息到达的代理变量。随后大多数的实证研究都证明了金融市场中成交量与价格波动之间具有正相关关系[1, 4-6]。近年来实证研究发现金融市场的量价关系更多的受其他因素的影响,如交易者的特征和类型[7-8]、波动率的特征[9-12]以及交易次数和订单流不平衡[13-15]等。基于高频数据,Chan和Fong[13]研究了已实现波动率与成交次数和平均交易头寸的关系。在此基础上,Chevallier和Sévi[10]、Giot等[11]将已实现波动率分解为连续部分和跳跃部分,研究了已实现波动率各部分与成交量、成交次数、平均交易头寸之间的相关关系。Slim和Dahmene[16]基于修正的MDH模型,将成交量分解为信息性成交量和流动性成交量,已实现波动率分解为连续部分和跳跃部分,进一步探究了成交量各部分与波动率各部分之间的量价关系。
国内对量价关系的研究多集中在因果检验上,通过Granger因果检验验证价格波动与成交量之间是否存在线性或非线性的因果关系,如王承炜和吴冲锋[17]、张维和闫冀楠[18]。随着高频数据应用的推广,文凤华等[19]、郭梁和周炜星[20]基于高频数据对中国股市波动性和量价关系进行了大量研究。基于各种实证模型,许多学者进一步探究了中国股市或期货市场量价关系呈现的新特征,如黄健柏等[21]利用MF-DCCA方法研究了中国金属期货市场量价关系的多重分形特征;翟爱梅和周彤[22]考虑了交易行为的非理性特点,研究了基于市场参与者行为假设的股票市场量价关系;任燕燕和李劭珉[23]基于分位数回归(QR)模型分析了不同分位数水平下的收益率与成交量的关系。此外,针对近年来中国股市时常发生大幅波动的情形,吴吉林[24]构建了机制转换 Copula模型来研究极端市场条件下中国股市量价间的尾部相依性;石建勋等[25]基于不确定性视角考虑了股市大幅波动时结构变动等因素可能对量价关系产生的重大影响,研究发现量价关系存在显著的时间断点效应。
上述国内外关于量价关系的研究大多集中在股票市场,只关注了价格波动与成交量的关系,但没有考虑持仓量这一重要因素。持仓量作为期货市场独有的概念,更多的反映套期保值的情况和未知情交易的数量。通过分析持仓量的变化可以分析市场上多空力量的变化,对判断市场的走势有重要作用,因此对中国有色金属期货市场量价关系的研究不仅要关注波动率与成交量的关系,也要考虑持仓量的影响。国外关于持仓量的研究相对较早,早在1993年Bessembinder和Seguin[4]研究发现期货市场价格波动与成交量正相关,与持仓量负相关,持仓量的增大减缓了期货市场的价格波动。Girma和Mougoué[26]、Ripple和Moosa[27]通过对原油期货市场量价关系的研究发现不仅成交量对价格波动有显著影响,持仓量对价格波动也有显著影响。国内关于持仓量与价格波动的研究则相对较晚,但也取得了一些研究成果,如王彬和宋逢明[28]研究发现不知情交易者的持仓量变化和预期变化对价格波动有显著影响;田新民和沈小刚[29]研究发现持仓量与日内价格波动之间存在负相关关系,未预期成交量、未预期持仓量对价格波动的影响比预期成交量、预期持仓量对价格波动的影响大的多。
纵观上述国内外关于持仓量与价格波动的研究,大都是基于日度数据的研究,而基于高频数据对持仓量与价格波动关系的研究则相对较少。Avramov等[30]研究发现在波动率对成交量的回归方程中使用高频数据比使用日度数据有超过两倍的解释能力,基于高频数据的已实现波动率可以作为日波动率的更稳健的估计量。国内学者通过超高频数据对量价关系也有所研究,但主要侧重于即时价格影响[31-34],且基于高频数据量价关系的研究大多集中在股票市场或能源期货市场,针对商品期货尤其是有色金属期货市场量价关系的研究相对较少,而有色金属期货市场在中国产业结构和国民经济中的重要地位使得针对中国有色金属期货市场量价关系的研究更加重要和迫切。因此借鉴Bessembinder和Seguin[4]以及Slim和Dahmene[16]的研究成果,将成交量和持仓量分别分解为可预期部分和非可预期部分,基于高频数据研究了中国有色金属期货市场上成交量和持仓量各部分对价格波动的影响,全面揭示了中国有色金属期货市场中量(成交量和持仓量)与价(价格波动)之间的动态关系。
2 模型构建
本文首先给出期货市场价格波动的有效度量:已实现波动率,然后通过建立量价关系基础模型、基于成交量和持仓量分解的量价关系模型以及量价关系非对称模型考察中国有色金属期货市场的量价关系,即研究日已实现波动率与成交量、持仓量以及各分解部分的关系。
2.1 已实现波动率
已实现波动率的估计方法无模型,无参数,且在一定条件下是积分波动率的无偏估计,因而受到国内外学者的广泛关注。Chan和Fong[13]研究发现已实现波动率可以更好地刻画成交量与价格波动之间的关系。因此本文在研究中国有色金属期货市场量价关系时,选取已实现波动率作为期货市场价格波动的有效度量。
将一天交易时间等间隔取M个观察点,则基于高频数据的已实现波动率定义为日内高频收益平方之和,即:
(1)
其中rt,j为第t个交易日第j个时间段的收益率,定义为rt,j=100×(ln(pt,j)-ln(pt,j-1)) .
然而,该已实现波动率只能反映交易时段的价格波动,而不能反映非交易时段的价格波动,即市场从第一天收盘到第二天开盘的价格波动。因此,借鉴Hansen和Lunde[35]的方法,引入尺度参数c对已实现波动率进行变换,使其更好地刻画全天的真实波动率,则修正后的第t天的已实现波动率为:
(2)
2.2 量价关系基础模型
基于高频已实现波动率,Giot等[11]、Chevallier和Sévi[10]、Slim和Dahmene[16]研究了价格波动与成交量的关系,但没有研究其与持仓量的关系,而Bessembinder和Seguin[4]、 Girma和Mougoue[26]以及Ripple和Moosa[27]的研究均表明价格波动不仅与成交量有密切关系,也与持仓量有密切关系。因此,为了研究价格波动与成交量、持仓量以及成交相对增量、持仓相对增量的关系,借鉴Giot等[11]、Chevallier和Sévi[10]、Slim和Dahmene[16]的研究方法,建立如下模型:
(3)
(4)
其中RVt为前面定义的已实现波动率,波动率的滞后项是考虑了已实现波动率的持续性和强自相关性。在模型设定中通常选择滞后12阶来消除已实现波动率的自相关性,这已经成为一种惯例。因此本文参考前人的研究成果,选择连续滞后12阶来消除已实现波动率的自相关性。同时考虑周内新信息的释放可能引起的价格波动,引入周三虚拟变量DUMMYi,t,即当交易时间为周三时取值1,其余交易时间取值0。Vi,t和Ii,t分别是期货i第t天的对数成交量和对数持仓量。vi,t和ii,t分别对应期货i第t天的成交相对增量和持仓相对增量,其定义分别为:vi,t=100×(Vi,t-Vi,t-1),ii,t=100×(Ii,t-Ii,t-1)。
2.3 基于成交量和持仓量分解的量价关系模型
外来信息会引起期货市场价格的波动,而未来的信息是无法预期的,所以预期到的成交量和非预期成交量对价格波动的影响是不同的,对持仓量同样如此。因此为了更进一步探究中国有色金属期货市场价格波动与成交量、持仓量各部分之间的关系,借鉴Bessembinder和Seguin[4]的研究成果,将成交量和持仓量分别分解为可预期部分和非可预期部分,探究预期成交量和非预期成交量以及预期持仓量和非预期持仓量对价格波动的不同影响。为了消除成交量和持仓量的序列自相关,利用自回归移动平均模型ARIMA(p, q)对成交量和持仓量进行回归:
(5)
(6)
其中预期部分为通过ARIMA(p, q)模型计算出的拟合值,非预期部分是其实际值与拟合值之差。ARIMA模型中滞后项的选择基于AIC准则和SC准则,确定最合适的p和q值。经比较分析,对铜期货成交量选择ARMA(2, 1) 模型,对铝期货成交量选择ARMA(4, 1) 模型;对铜期货持仓量选择ARMA(1,0) 模型,对铝期货持仓量选择ARMA(2, 1) 模型。然后将预期成交量、非预期成交量以及预期持仓量和非预期持仓量引入量价关系基础模型,得到
(7)
其中EVi,t、UVi,t、EIi,t、UIi,t分别为预期成交量、非预期成交量、预期持仓量和非预期持仓量。
2.4 量价关系非对称模型
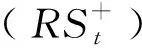
(8)
(9)
Bessembinder和Seguin[4]研究发现正的成交量冲击对金融市场波动的影响比负的成交量冲击影响更大,对持仓量的不同冲击也是如此。因此为了进一步探究正的成交量冲击和负的成交量冲击以及正的持仓量冲击和负的持仓量冲击对中国有色金属期货市场价格波动的不同影响,在模型(7)的基础上建立如下模型:
(10)
考虑到上述量价关系模型的估计结果的残差可能存在异方差性和自相关性,在估计方法的选择上选用OLS with Newey West估计方法进行参数估计。最后对模型估计结果进行分析并归纳总结中国有色金属期货市场的量价关系。
3 实证分析
3.1 数据和基本统计量分析
本文选取两种最典型的中国有色金属期货:铜期货和铝期货为例,基于一分钟高频交易数据进行实证分析。时间跨度为2010年7月1日至2015年7月1日(除去节假日,共计1214个交易日),研究对象为上海期货交易所三个月到期的铜铝期货,数据来源于国泰安数据库。上海期货交易所的交易时间为上午9:00到11:30以及下午13:30到15:00,每天共计227个时间间隔,即M=227。数据指标包括交易时间、开盘价、收盘价、成交量、持仓量等。对部分缺失数据,用均值插值法将缺失数据补齐。

表1 中国有色金属期货各指标描述性统计分析
表1列出了铜铝期货各指标的描述性统计量,结果表明上偏已实现半方差和下偏已实现半方差的均值基本为已实现波动率的一半,且下偏已实现半方差的均值略大于上偏已实现半方差的均值,说明铜铝期货市场上价格下跌的风险要大于价格上涨的风险,也从侧面反映出期货市场的投资者倾向于做空。由单位根检验知,成交量和持仓量序列是平稳的,故在后面的分解中可以直接将成交量和持仓量通过ARIMA模型分解为可预期部分和非可预期部分。另外,除预期成交量和预期持仓量外,各统计量在滞后12阶后仍存在很强的自相关性, 从而奠定了量价关系模型的统计基础。
3.2 回归结果和讨论
对中国铜铝期货量价关系基础模型、基于成交量和持仓量分解的量价关系模型和量价关系非对称模型的估计结果如表2所示。研究结果表明,价格波动与成交量、持仓量的关系在铜铝期货市场上几乎呈现相同的规律,反映周内新信息释放的周三虚拟变量的系数在所有回归方程中都是显著的,说明周内新信息的释放对期货市场价格波动有显著影响。下面对三类模型具体分析如下
3.2.1量价关系基础模型估计
铜铝期货价格波动与成交量、持仓量以及成交相对增量和持仓相对增量的关系见表2量价关系基础模型(3)和(4)。首先对量价关系基础模型(3)分析如下:成交量与价格波动的系数在1%显著性水平下显著为正,即成交量对价格波动有显著正向影响,说明了成交量作为反映到达市场信息多少的指标,成交量放大,到达市场的信息增多,从而加剧市场的价格波动,成交量与价格波动之间存在“价量齐涨”和“价量齐跌”的规律。持仓量与价格波动的系数在1%显著性水平下显著为负,即持仓量与价格波动之间显著负相关,说明了持仓量作为反映市场深度和流动性的指标,更多的是反映未知情交易的情况和套期保值的情况,持仓量的增大使得市场深度增大,从而减缓了市场波动。
表2中国铜铝期货量价关系模型的估计结果

注:其中括号内为稳健标准误差,***、**、*分别表示在1%、5%、10%的水平上显著;下同。
量价关系基础模型(4)反映了铜铝期货市场价格波动与成交相对增量、持仓相对增量的关系。参数估计结果显示了与模型(3)相似的规律,即铜铝期货市场价格波动与成交相对增量呈显著正相关关系,与持仓相对增量呈显著负相关关系,说明成交量变化越大,价格波动就会越大,而持仓量变化则与价格波动的变化方向相反。可见,中国有色金属期货市场的价格波动与成交量、成交相对增量呈显著正向关系,与持仓量、持仓相对增量呈显著负向关系。
3.2.2基于成交量和持仓量分解的量价关系模型估计
铜铝期货基于成交量和持仓量分解的量价关系模型估计结果见表2分解模型(7)。参数估计结果表明:预期成交量和非预期成交量都与期货市场价格波动之间呈现显著正相关关系(对铜期货而言,预期成交量在10%显著性水平下显著而非预期成交量在1%显著性水平下显著;对铝期货都在1%水平下显著),且非预期成交量的系数(铜期货为1.411;铝期货为0.580)显著大于预期成交量的系数(铜期货为0.275;铝期货为0.338),说明非预期成交量对有色金属期货市场价格波动的正向影响要显著大于预期成交量对期货市场价格波动的正向影响。预期持仓量和非预期持仓量都与期货市场的价格波动之间存在显著负相关关系(铜铝期货预期持仓量在10%显著性水平下显著,非预期持仓量在1%显著性水平下显著),且非预期持仓量对期货市场价格波动的负向影响要显著大于预期持仓量对期货市场价格波动的影响(对铜期货,2.704显著大于0.446;对铝期货,1.097显著大于0.201)。这是因为外来信息会引起期货市场的价格波动,而未来的信息是投资者无法预期到的,所以预期成交量(持仓量)和非预期成交量(持仓量)对价格波动的影响是不同的,且一般而言非预期部分会对价格波动造成更大的影响,实证估计结果也恰恰诠释了这一点。这表明中国有色金属期货市场的价格波动主要是由代表新信息的非预期成交量和非预期持仓量引起的。此外,预期成交量(持仓量)反映了期货市场中知情交易者的比例,非预期成交量(持仓量)反映了期货市场中流动性交易者的比例,从另一个侧面说明,中国有色金属期货市场中,相比知情交易者的比例,有更大比例的流动性交易者,这与市场流动性理论的表述相吻合。
3.2.3量价关系非对称模型估计
铜铝期货量价关系非对称模型估计结果见表2非对称模型(8)、(9)、(10)。对关于波动率的量价关系非对称模型(8)的估计结果表明:成交量和持仓量的非预期部分对上(下)偏已实现半方差的影响显著大于其预期部分对上(下)已实现半方差的影响,这与模型(7)的解释是相同的。从对应的拟合优度(R2)可以看出成交量、持仓量分解部分对上偏已实现半方差和下偏已实现半方差有不同的解释力,然而出乎意料的是成交量、持仓量分解部分对上偏已实现半方差的拟合优度要明显好于其对下偏已实现半方差的拟合优度(对铜上偏已实现半方差的R2为0.5286显著大于对下偏已实现半方差的R20.3764;对铝,则为0.3936显著大于0.1606),说明成交量、持仓量对铜铝期货上偏已实现半方差的解释力度高于其对下偏已实现半方差的解释力度,也间接说明了在中国有色金属期货市场上,相比于价格下跌的风险,人们更关注价格上涨的风险,成交量和持仓量对价格上涨的风险有更好的解释力和预测能力。另一个有趣的发现是周内信息释放对价格波动的影响对铜铝期货市场是不同的。具体而言,铜期货市场周内信息释放对下偏已实现半方差在5%显著水平下有显著影响,但对上偏已实现半方差无显著影响。而铝期货市场周内信息释放对上偏和下偏已实现半方差都有显著影响(显著性水平分别为1%和10%)。说明铜期货市场的投资者更容易受价格下跌风险的影响。
关于成交量和持仓量的非对称量价关系模型(9)、(10)的估计结果表明:预期成交量和非预期成交量对期货市场的价格波动都有显著正向影响,正的非预期成交量的系数(对铜期货为1.355;对铝期货为0.964)显著为正,且明显大于预期成交量和非预期成交量的系数(对铜分别为0.322和0.902;对铝分别为0.369和0.127),说明正的成交量冲击对价格波动的影响要大于负的成交量冲击对价格波动的影响。预期持仓量和非预期持仓量对期货市场价格波动都有显著负向影响,正的非预期持仓量冲击的系数显著为负(对铜期货为-3.968;对铝期货为-2.923),且其绝对值明显大于预期持仓量和非预期持仓量的系数绝对值(对铜期货分别为-0.445和-1.561;对铝期货分别为-0.171和-0.343),说明正的持仓量冲击对价格波动的影响要明显大于负的持仓量冲击对价格波动的影响。
3.3 稳健性检验
为了加强结果的稳健性,考虑到可能存在的条件异方差,通过引入GARCH误差结构,重新估计了上述三类量价关系模型。稳健性检验估计结果见表3,结果表明其定性的结果分析与之前的分析是相似的,且ARCH 系数和GARCH系数都是显著的,说明量价关系模型具有显著的条件异方差性。
4 结语
本文以上海交易所铜铝期货为例,基于高频数据研究了中国有色金属期货市场价格波动与成交量、持仓量的关系。借鉴Bessembinder和Seguin[4]的研究方法,将成交量和持仓量分解为可预期部分和非可预期部分,探讨了成交量和持仓量可预期部分和非可预期部分对有色金属期货市场价格波动的影响。考虑到成交量、持仓量对上偏和下偏已实现半方差的不同影响以及成交量和持仓量的不同冲击对价格波动的不同影响,进一步研究了中国有色金属期货市场上量价关系的非对称性。
研究结果表明中国有色金属期货市场的价格波动与成交量和成交相对增量之间均存在显著正相关关系,与持仓量和持仓相对增量之间均存在显著地负相关关系,即成交量与价格波动之间存在“价量齐涨“和“价量齐跌”的规律,而持仓量与价格波动的关系则相反。成交量的变化对价格波动有正向影响而持仓量的变化对价格波动则有负向影响。价格波动与预期成交量(持仓量)和非预期成交量(持仓量)都有显著正(负)相关关系,且非预期成交量对价格波动的正(负)向影响要明显大于预期成交量对价格波动的影响。说明中国有色金属期货市场的价格波动主要是由代表新信息的非预期成交量和非预期持仓量引起的。中国有色金属期货市场的量价关系存在一定程度的非对称特征,即成交量和持仓量对上偏已实现半方差的影响要显著大于它们对下偏已实现半方差的影响,正的成交量(持仓量)冲击对价格波动的影响要大于负的成交量(持仓量)冲击对价格波动的影响。研究结果对投资者以及市场监管者判断价格波动趋势、分析投资决策和政策制定提供借鉴,具有重要的指导意义和研究价值。

表3 中国铜铝期货量价关系模型的稳健性检验(GARCH误差结构)
