三维水流作用下哑铃型围堰周围海床局部冲刷

2018-07-12段伦良王少华张启博郑东生

西南交通大学学报 2018年4期

段伦良,　王少华,　张启博,　郑东生

(西南交通大学土木工程学院, 四川成都 610031)

局部冲刷是结构物扰动水流而引起漩涡冲蚀结构物周围海床的一种水力学现象.冲刷会使河床下切、基底床沙被掏空,进而降低结构物基础承载力.结构物因水流冲刷造成的破坏现象已屡见不鲜[1],不但给人民生命财产构成了威胁,而且也给国家造成了极大的经济损失.因此,研究结构物周围的局部冲刷非常必要.

近年来,国内外学者对流固土相互作用理论及局部冲刷均做了大量研究[2-13],目前对结构物周围的局部冲刷机理及影响因素基本达成了共识.在冲刷机理方面,一般认为水流受到结构物的扰动作用会在结构物周围产生漩涡,结构物周围产生的漩涡会卷起泥沙,然后再由水流挟带至下游,从而使得结构物周围发生局部冲刷坑.局部冲刷坑的出现会进一步影响结构物周围的流场特性,使得流场结构发生变化.随着冲刷坑的发展,结构物周围流速降低,水流挟沙能力减弱,当泥沙对水流的抗冲刷能力与被阻水流对床沙的侵蚀能力达到平衡时,冲刷完成,形成最终的冲刷坑.结构物周围局部冲刷的影响因素主要包括河道形态、结构物大小与形状、床沙特性及水流特性等.虽然以往对局部冲刷已做过大量研究,然而大部分研究主要针对桥墩、丁坝、管线、防波提等结构物,很少涉及围堰.实际上,跨海桥梁在建设过程中多借助围堰来进行承台施工,围堰作为一种大尺度结构物,必然会对周围水流产生较大的扰动作用,进而导致其周围产生局部冲刷现象,而围堰周围的局部冲刷可能会使围堰本身发生倾斜,此外,围堰周围海床的冲刷也会对桥梁基础及地基承载力构成威胁,因此研究围堰周围海床的局部冲刷对保证桥梁安全具有重要意义.为此,于长海等[14]基于嘉绍大桥施工采用的圆形围堰研究了围堰周围的局部冲刷及纠偏方案;韩海骞等[15]研究了涌潮作用下围堰周围的局部冲坑形成过程、冲刷坑形态及最大冲刷深度;樊俊生[16]以芜湖大桥为工程依托,研究了不同施工周期时的冲刷计算曲线,上述研究未考虑围堰吃水深度对局部冲刷的影响.陈述[17]以天兴洲大桥为工程背景,研究了围堰下沉过程中局部冲刷坑形态随入水深度的变化,主要针对水流作用下的圆截面围堰,围堰截面形状相对简单.据已有研究结果得知,结构几何特征对海床局部冲刷影响较大,因此本文将以复杂截面形式的哑铃型围堰为研究对象,对其处于不同吃水深度时周围海床的局部冲刷问题展开讨论.

为研究三维水流作用下哑铃型围堰周围的局部冲刷,借助CFD软件Flow-3D建立海床冲刷模型,进一步探讨了哑铃型围堰周围流场的分布特点及周围海床的局部冲刷形态,为跨海桥梁围堰定位及基础稳定性分析提供参考.

1　模型建立

基于CFD软件Flow-3D进行数值建模,以RANS方程作为控制方程,采用速度入口法建立三维水流模型,同时利用VOF法捕捉自由液面.由于Flow-3D软件采用了FAVOR网格处理技术,因此在控制方程中加入了面积分数与体积分数.对于不可压缩三维水流模型,其控制方程为

(1)

(2)

(3)

(4)

式中:ux、uy、uz分别为x、y、z方向的速度;Ax、Ay、Az分别为x、y、z方向可流动的面积分数;VF为可流动的体积分数;ρ为流体密度;gx、gy、gz分别为x、y、z方向的重力加速度;fx、fy、fz分别为x、y、z方向的粘滞力加速度;t为时间.

由于本文主要研究结构物周围的泥沙运动,因此选用RNGk-ε模型实现湍流封闭,引入面积参数和体积参数后的RNGk-ε方程为

PT+GT+DT-εT,

(5)

(6)

式中:kT为紊动能;εT为紊动耗散率;PT为速度梯度引起的湍动能k的产生项,默认取0;GT为由浮力所产生的紊动动能的产生项,对于不可压缩流体,GT取值为0;C1=1.44;C2=1.92;C3=0.2;DT为紊动能扩散项;Dε为耗散率扩散项具体可由式(7)、(8)表示.

(7)

(8)

式中:vk=1.39;vε=1.39;R=1;ξ=0.

关于泥沙运动方程的描述参考文献[18],控制方程包括推移质输沙律方程和悬移质输沙方程,具体表达式为

(9)

(10)

τ=0.5cρ(u12+u22+u32),

(11)

τcr=φ(rc-r)d,

(12)

式中:c为常系数,取值为0.19;u1、u2、u3分别为海床表面附近水平、垂向和横向脉动流速;φ为临界希尔兹参数;rc为泥沙容重;r为水的容重.

几何轮廓如图1所示,其中:u0为水流速度;dw为水深;hm为哑铃型围堰的吃水深度;hs为海床厚度;h为哑铃型围堰高度.

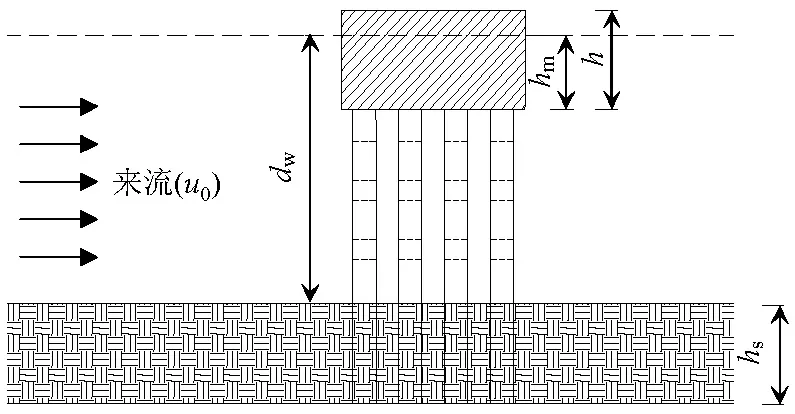
图1　几何轮廓Fig.1　Sketch of scour around a cofferdam

文中围堰几何尺寸参考某大桥桥台施工所采用的哑铃型围堰,其具体几何特征如图2所示.

图2　哑铃型围堰几何尺寸Fig.2　Dimensions of the dumbbell-shaped steel suspending cofferdam

图2中:L1为围堰在垂直水流方向的尺寸;L2为围堰在水流方向的尺寸;a为钢护筒在水流方向的间距;b为钢护筒在垂直水流方向的间距;r0为钢护筒的半径.

2　模型验证

模型验证部分主要包括:流动模型验证与冲刷模型验证,为验证流动模型的正确性,将本文模型底面变为光滑床面,然后仿照Roulund等[19]试验进行数值模拟,并将数值计算的流速断面分布与Roulund等试验结果作比较,比较结果如图3所示,通过图3可看出,本文数值结果与Roulund等试验结果基本吻合,说明本文流动模型合理可靠.流动模型验证过程中参数取值分别为:圆柱直径dc1=0.536 m;dw=0.54 m;u0=0.33 m/s.

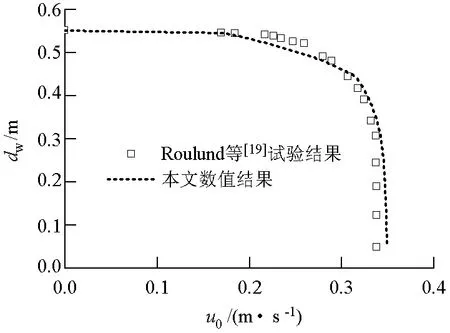
图3　流速断面对比Fig.3　Comparison of the velocity distributions

为验证冲刷数值模型的合理性,将本文模型与Melville[20]单柱试验的经典试验结果进行对比.Melville试验中:水槽长L=19 m;宽度W=45.6 cm;圆柱形桥墩直径dc2=5.08 cm;泥沙平均粒径d50=0.385 cm;u0=0.25 m/s;床面倾角θs=1/10 000.试验模型平面布置如图4所示.

在模型验证过程中,首先将Melville 试验结果中距离海床表面2 mm的桥墩周围流线图与本文数值结果进行对比,然后再将Melville 试验结果中水流冲刷30 min时冲刷深度与本文模型结果对比.

图4　试验布置平面图Fig.4　Layout of Melville’s experiment

图5分别给出了距离海床表面2 mm处Melville 试验结果中的流线图及本文数值模型中的流速矢量图.由图5可以看出,在圆柱形桥墩的背侧靠近中心线处均有漩涡产生,本文数值模拟结果中桥墩周围的流场分布与Melville 冲刷试验结果基本吻合.

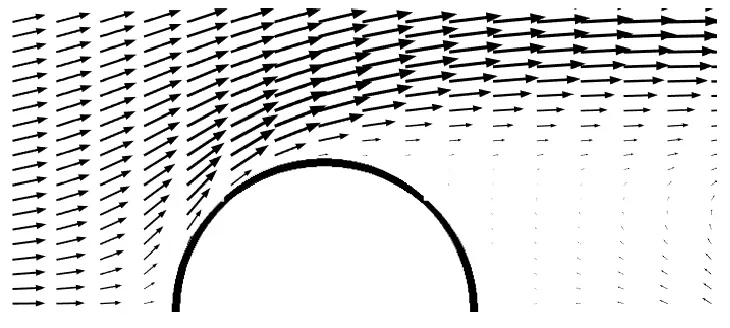
(a) 本文数值模型中桥墩周围流速矢量分布

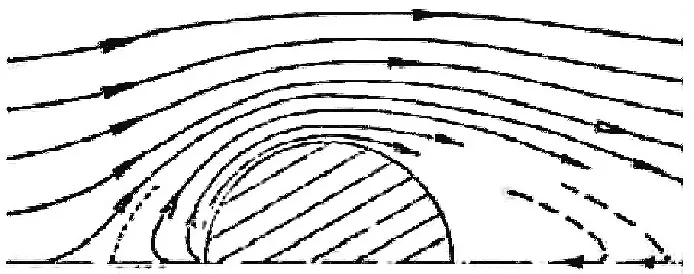
(b) Melville 冲刷试验中桥墩周围的流线分布图5　桥墩周围流场分布Fig.5　Distribution of the flow field around the pier

冲刷时间为30 min时,Melville 试验结果中的最大冲刷深度为4 cm,而本文数值模型计算得到的冲刷形态如图6所示,其最大冲刷深度发生在桥墩侧面80°左右,为4.3 cm.因此本文数值结果中最大冲深位置和最大冲刷深度均与Melville 试验结果接近.进一步说明了本文冲刷模型计算结果可信度较高.

根据上述流动模型、冲刷模型的对比结果,可说明本文模型合理可靠,可为后续研究奠定基础.

(a) 立面图

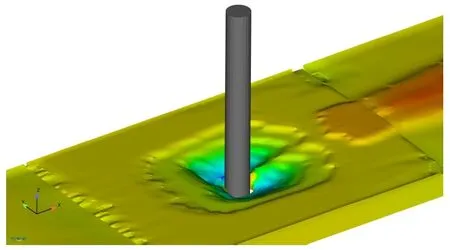
(b) 轴侧图图6　桥墩周围冲刷形态Fig.6　Scour patterns around a bridge pier

3　哑铃型围堰周围流场及冲刷研究

以往关于结构物周围海床局部冲刷的研究,主要针对桥墩、桥台、防波堤、管线等结构物,而关于围堰周围的冲刷研究相对较少.虽然局部冲刷原理类似,但结构物几何特征对周围海床冲刷影响较大.针对此现状,以在建的某大桥承台施工采用的哑铃型围堰为研究对象,并借助Flow-3D软件建立了围堰周围海床的局部冲刷模型.首先分析了围堰周围流场的分布特征,然后分别讨论了吃水深度及水流速度对围堰周围海床局部冲刷的影响.

基于Flow-3D软件建立的哑铃型围堰周围海床局部冲刷模型的几何轮廓如图7所示,其中左侧设置为入流边界,可以输入流速,右侧设置为出流边界,通过控制出流处的水面高程来设置出流边界,前后侧均为对称边界,顶面设置为对称边界,底面设为壁面边界.

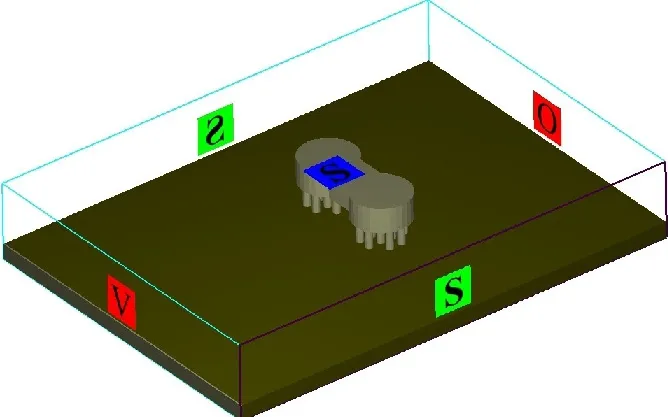
图7　围堰周围海床局部冲刷模型Fig.7　Profile of the scour model around the dumbbell-shaped steel suspending cofferdam

几何模型建立完成后,基于Flow-3D软件自带的FAVOR网格处理技术进行网格划分,并在哑铃型围堰周围进行局部网格加密,为验证网格分辨率,图8给出了不同网格密度下(以网格总数N表示),冲刷时间为5 000 s时围堰周围的最大冲刷深度分布(u0=1.0 m/s).由图8可以发现,网格总数在 840 000时,最大冲刷深度值基本稳定,说明采用的网格密度较合理(数值模型中网格总数为840 000).网格划分过程中均采用方形网格,不同区域内网格尺寸不同,表1进一步给出了本文数值模型中网格尺寸在不同区域内的大小.

图8　不同网格密度下围堰周围海床最大冲刷深度Fig.8　Maximum scour depths around the cofferdam with various mesh systems

沿x方向流场位置/m0～260260～400400～500网格尺寸/m2.00.52.0

本文在研究过程中如未特别说明,相关参数按表2取值

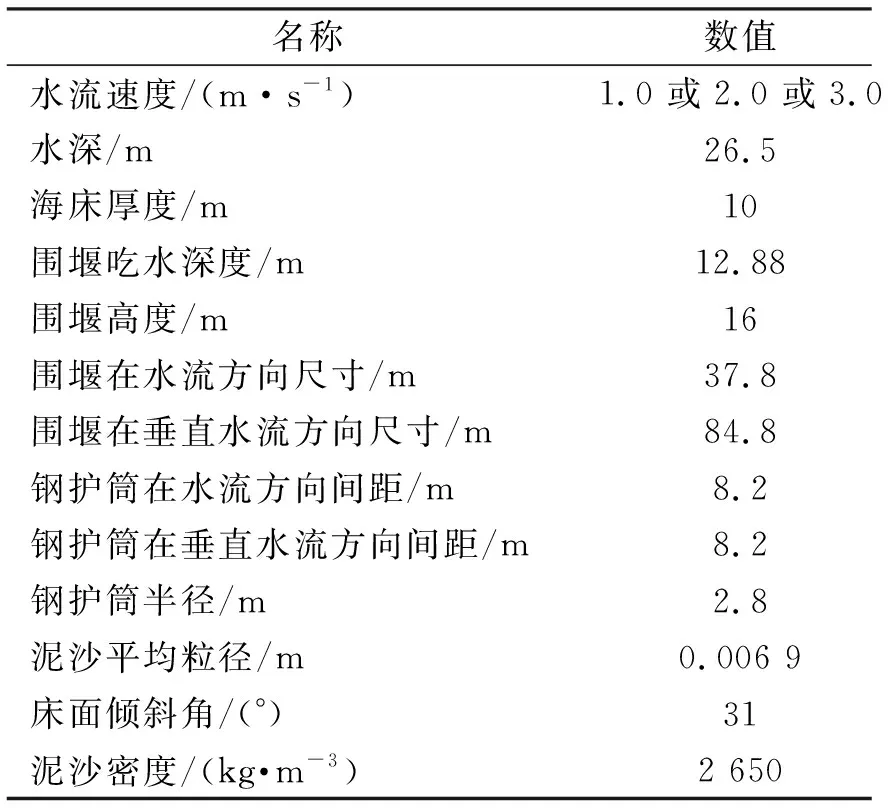
表2　数值案例所取参数Tab.2　Parameters used in numerical examples

3.1　哑铃型围堰周围流场特征

结构物周围流场的改变不但会影响作用于结构物本身的水动力荷载,也会影响周围海床的局部冲刷,因此分析结构物周围流场特征是研究结构物周围海床局部冲刷的前提,本文将首先对哑铃型围堰周围的流场分布特征展开探讨.

通过数值测试发现,围堰周围海床的局部冲刷在70 min左右达到平衡,因此本文冲刷模型计算时间均设定为5 000 s.图9、10分别给出了流速大小为2.0 m/s、吃水深度为12.88 m时围堰及钢护筒附近的流速矢量分布及其对应的流线分布,其中图9(a)、10(a)为围堰周围流场分布的俯视图(图10(a))中流线相交是因为图10(a)中具有不同高程的流线),图9(b)、10(b)为钢护筒周围流场分布的俯视图.

(a) 围堰

(b) 钢护筒图9　围堰及钢护筒周围流速矢量分布Fig.9　Velocity vector field around the dumbbell-shaped steel suspending cofferdam and the steel casings

由图9得知:水流运动过程中受到围堰的阻碍时,一部分水流会直接流向围堰前方,然而直接流到围堰前方的水流速度会减小;另一部分水流绕过围堰向前继续流动;流速在围堰两侧75°～85°的地方最大.

从图10(a)可以看出,在围堰前方与后方均会有漩涡产生,然而围堰后方漩涡较前方更加明显,通过图10(b)可以发现,钢护筒周围也有漩涡产生,但是前排钢护筒的尾涡较后排尾涡更加突出,前排护筒对后排护筒的遮蔽效应影响了其周围的流场分布.

(a) 围堰

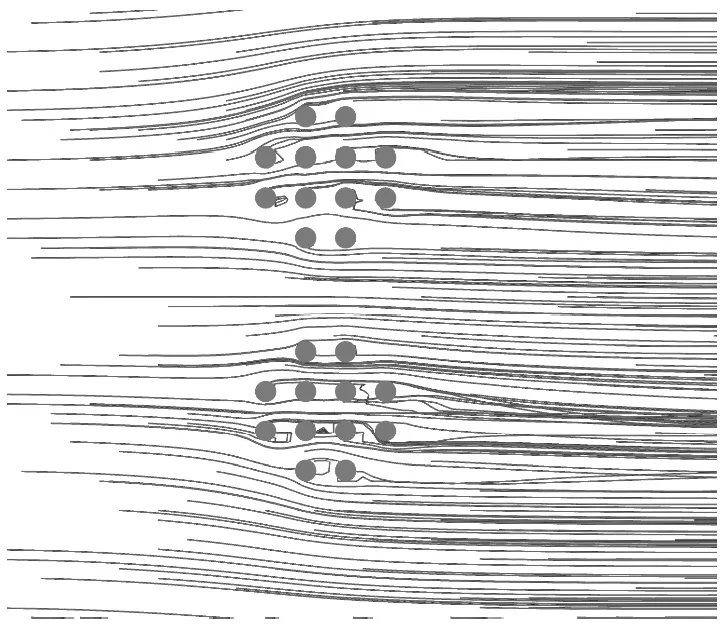
(b) 钢护筒图10　围堰及钢护筒周围流线分布Fig.10　Streamlines around the dumbbell-shaped steel suspending cofferdam and the steel casings

3.2　吃水深度对围堰周围海床冲刷的影响

受地形、水文等条件影响,不同桥址处承台的设计高程可能不同,即承台施工过程中围堰的吃水高度可能会发生变化.因此本文将对处于不同吃水深度的哑铃型围堰周围的冲刷情况展开研究.

研究过程中,吃水深度分别取6.88、8.38、9.88、11.38、12.88、14.38、15.88 m,水流速度取2.0 m/s.图11给出了冲刷5 000 s时哑铃型围堰吃水深度与最大冲刷深度的关系.

由图11可以看出,随着吃水深度增大,哑铃型围堰周围海床的最大冲刷深度有所增大,但增量不剧烈.因此在围堰标高设计过程中,吃水深度对围堰周围海床冲刷的影响为次要因素,应把关注重点放在吃水深度对围堰所受水动力的影响.

3.3　不同流速下哑铃型围堰周围海床冲刷形态

据以往研究得知,流速及结构物几何特征均会对其周围海床局部冲刷造成很大影响,因此本文将针对几何特征复杂的哑铃型围堰,研究不同流速下其周围的海床冲刷形态.

在研究过程中,流速分别取1.0、1.5、2.0、2.5、3.0、3.5、4.0 m/s,吃水深度取12.88 m.图12给出了冲刷时间为5 000 s时,不同流速下哑铃型围堰周围海床的最大冲刷深度.

图13为不同流速下哑铃型围堰周围海床冲刷形态的轴侧图.

由图12、13可以看出:流速大小对围堰周围海床的局部冲刷影响显著,最大冲刷深度随流速增大而增大;冲刷坑平面形态近似哑铃形,且围堰周围海床冲的冲刷影响范围受流速影响较大;随着离围堰沿水流方向中心线距离的增加,冲刷深度先减小后增加,最大冲刷深度出现在距离围堰沿水流方向中心线最近的钢护筒附近.

图11　不同吃水深度下围堰周围最大冲刷深度Fig.11　Variations in the maximum scour depth with the submerged depth of the cofferdam

图12　不同流速下最大冲刷深度Fig.12　Maximum scour depth atvarious current velocities

以围堰这类特殊结构为研究对象,研究了水流作用下围堰周围的冲刷形态,可为工程中分析围堰的稳定性提供参考.然而实际海洋环境中波流、潮流等因素经常同时存在,涉及到的影响因素较多,关于复杂海洋环境下围堰的局部冲刷现象,仍需要进一步探索.

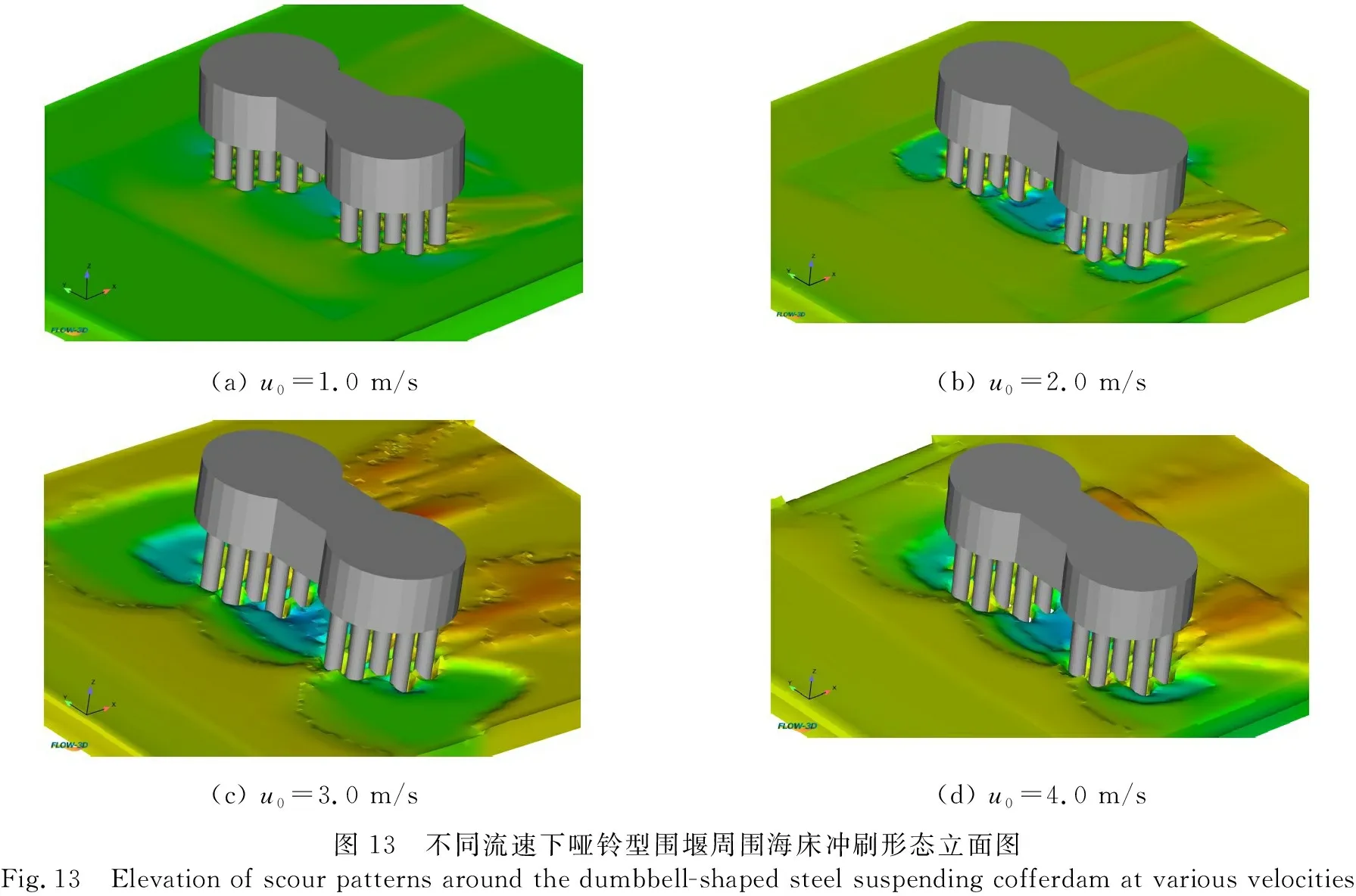
(a) u0=1.0 m/s(b) u0=2.0 m/s(c) u0=3.0 m/s(d) u0=4.0 m/s图13 不同流速下哑铃型围堰周围海床冲刷形态立面图Fig.13 Elevation of scour patterns around the dumbbell-shaped steel suspending cofferdam at various velocities