波形顶板-UHPC组合桥面板优化设计
2018-07-12张清华程震宇廖贵星卜一之
张清华, 程震宇, 廖贵星, 卜一之, 李 乔
(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 中铁大桥勘测设计院集团有限公司, 湖北 武汉 430050)
作为现代桥梁工程的标志性创新成就,正交异性钢桥面板是现代桥梁中应用最广泛的桥面板结构形式之一.但自从英国Severn桥在1971年被报道其正交异性钢桥面板出现疲劳开裂问题以来,该类结构的疲劳开裂和桥面铺装损坏案例不断涌现,显著增加结构的全寿命周期成本,严重影响结构的使用性能和服役质量,已成为阻碍桥梁设计应用和可持续发展的控制性难题[1-7].国内外学者进行的大量研究表明:采用大纵肋正交异性钢桥面板结构,可以有效减少焊缝数量,改善结构的疲劳性能,但顶板与纵向加劲肋焊缝部位和横肋与纵向加劲肋连接部位仍是桥面板疲劳性能的控制部位[8-12];在正交异性钢桥面板上设置混凝土结构层构成组合桥面板结构体系,能够通过增加桥面板刚度以有效降低关键疲劳易损部位应力集中程度,从而显著改善正交异性钢桥面板疲劳开裂和桥面铺装易损问题[13-17].但直接在传统的正交异性钢桥面板上设置各类结构层,几何刚度不平顺和连接焊缝等应力集中突出部位仍然较多,仍存在较高的疲劳开裂风险.新型波形顶板-超高性能混凝土(ultra-high performance concrete, UHPC)组合桥面板有望从根本上解决正交异性钢桥面板所面临的主要矛盾,而良好的受力性能和结构设计是新结构应用的前提条件.通过参数效应分析确定影响结构力学性能的主要设计参数,提出基于BP(back propagation)神经网络的优化设计模型,对新型组合桥面板结构进行优化设计,在此基础上对其疲劳性能进行了研究.
1 新型组合桥面板和关键参数确定
1.1 波形顶板-UHPC组合桥面板
正交异性钢桥面板发展面临的主要矛盾有:(1) 高承载力与高疲劳病害风险之间的矛盾;(2) 具有竞争力的建设期经济性和欠佳的全寿命周期性能及成本之间的矛盾.矛盾的根源在于正交异性钢桥面板欠佳的疲劳性能.局部轮载作用导致的应力集中以及由桥面板鼓曲变形所引起的重要焊缝部位的次应力是导致正交异性钢桥面板疲劳开裂的主要内因,而反复的轮载作用和初始焊接缺陷则是正交异性钢桥面板疲劳病害频发的外因.因此,提高正交异性钢桥面板疲劳性能的主要途径在于增加桥面板顶板刚度和减少焊缝数量.综合考虑上述两大途径,发展新型桥面板结构体系是促进正交异性钢桥面板应用并推动其可持续发展的主要途径[3-11].
传统正交异性钢桥面板协同受力体系主要由顶板、闭口纵肋和横肋(隔板)组成,在满足桥面板受力性能和局部刚度基本要求的同时,也使得该类结构的构造和受力变得复杂.在大量的连接焊缝和几何刚度过度不平顺处,应力集中问题突出,严重影响结构的疲劳性能.在保证结构受力性能的条件下,最大限度减少几何刚度过度不平顺部位数量和焊缝数量是发展新型桥面板结构体系的根本目标.采用波形顶板代替顶板-U肋结构,同时在其上铺设高性能混凝土,构成组合受力体系,使桥面板具有足够的承载能力、局部竖向刚度和抗扭刚度.同时波形钢板高度远小于传统U肋高度,在反复轮载作用下,由波形顶板转动引起的波形板底部连接焊缝的应力幅不足以对其疲劳性能产生明显影响,因此可以省去横肋(隔板)的开孔自由边,实现波形板和横肋的连续自动化施焊.此时,焊缝数量将大幅度减少,由纵肋与顶板疲劳细节和纵肋与横肋交叉部位疲劳细节等控制结构疲劳性能的局面有望得到根本改善,从源头上提高桥面板的疲劳性能并解决其疲劳问题.
由于桥面板直接承受轮载的局部作用,受力复杂、应力集中问题突出,对于结构层材料的强度、抗裂性和耐久性提出了较高要求.超高性能混凝土作为新型水泥基复合材料,具有高抗拉和抗压强度、高弹性模量、高延性、高韧性、高耐久性等特点,是适用的新型组合桥面板结构层材料[15-17].此外可靠的钢混连接件是组合结构全寿命周期内协同受力的前提,组合销在欧洲的预制组合梁工程[18-19](preco-beam project)广泛应用,它由PBL(perfobond leiste)[20]发展而来,已被证明具备优异的疲劳性能和超高的承载力,其优化的开放边界有利于施工中的钢筋穿插安置,可引为新型桥面板结构体系的剪力连接件.采用波形顶板、组合销和UHPC结构层的组合桥面板可以称为“波形顶板正交异性钢板-组合销-UHPC组合桥面板”(后文简称“波形顶板-UHPC组合桥面板”),其构思如图1所示[21].

图1 波形顶板正交异性钢板-组合销-UHPC组合桥面板的构思Fig.1 Conceptual design of corrugated steel deck-composite dowel-UHPC orthotropic composite deck structure
1.2 主要设计参数对顶板结构力学特性的影响
波形顶板-UHPC组合桥面板横截面的主要设计参数包括:波形钢板高度h1、截面上部UHPC结构层厚度h2、波形钢板底部水平部位宽度b1、波形钢板弯起部分水平投影宽度b2、波形钢板顶部水平宽度b3以及板件折弯半径R,如图2所示.

(a) 顶板结构图
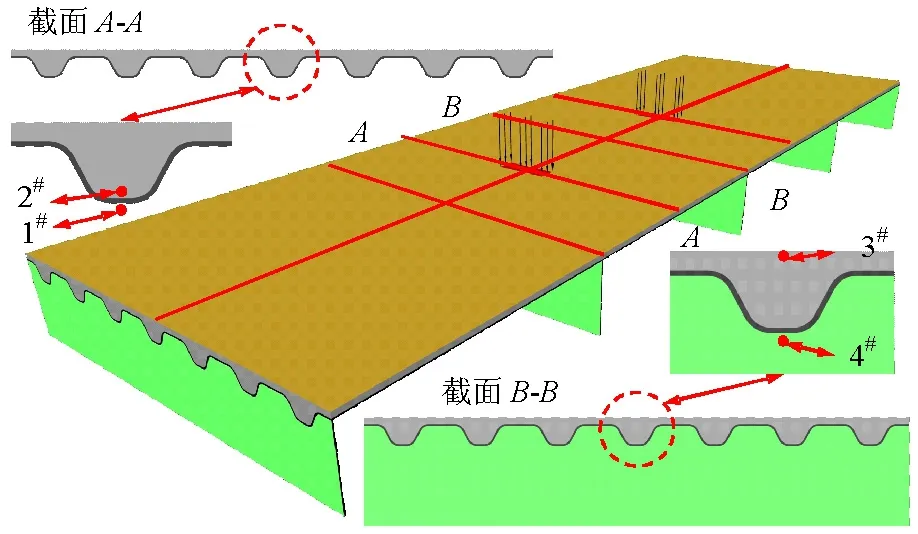
(b) 模型三维图图2 波形顶板-UHPC组合桥面板Fig.2 Corrugated steel deck plate-UHPC layer composite deck
根据UHPC组合桥面板的相关研究成果,通过计算分析,对新结构中UHPC结构层厚度h2的合理取值问题进行了研究.结果表明[21],其合理取值范围为40~60 mm.为简化分析,后续研究中将该值取为45 mm.横隔板间距l和多参数的耦合问题非常复杂,根据正交异性钢桥面板的发展趋势,将该值取为3 000 mm.参考传统正交异性桥面板的隔板尺寸,将横隔板高度取为840 mm,板厚为14 mm;参考传统U肋厚度,将波形顶板厚度取为8 mm,板件折弯半径取为板厚的5倍,即40 mm.
新型桥面板结构在多种桥梁结构类型中的研究结果表明[21],该桥面板在中等跨度和大跨度的多种桥型中具有良好的适用性.主要讨论局部荷载作用下结构的受力性能和结构优化设计问题.建立桥面板结构的参数化三维有限元模型,就各关键参数对于结构受力性能的影响问题进行了研究.为使考察点位置处的约束条件尽可能接近实际状态,分析模型纵向长度取为12 m,包含4个标准横隔板节间,横向包含7个标准波形节间.采用8节点实体单元模拟模型中UHPC结构层,采用4节点板壳元模拟钢板.采用组合销作为剪力件可以实现UHPC结构层和波纹顶板间的完全粘结,因此可忽略层间相对滑移,采用节点耦合模拟二者间的相互作用,不考虑材料非线性的影响.分析模型共有实体单元241 920个,板壳单元65 785个.在各道横隔板底部的两端施加Y方向约束并限制绕X轴的转动,在最右侧横隔板底端再施加Z方向约束,具体如图3所示.钢材的弹性模量和泊松比分别为2.1×1011Pa和0.3;UHPC的弹性模量和泊松比分别为5.5×1010Pa和0.19.选取最不利加载位置进行加载,在纵向施加两个车轮荷载,每个轮重70 kN,采用均布荷载方式施加,作用面积为600 mm×200 mm,作用于中间两跨的跨中,荷载中心距为1个横隔板间距长度.桥面板结构及其有限元分析模型分别如图2、3所示.
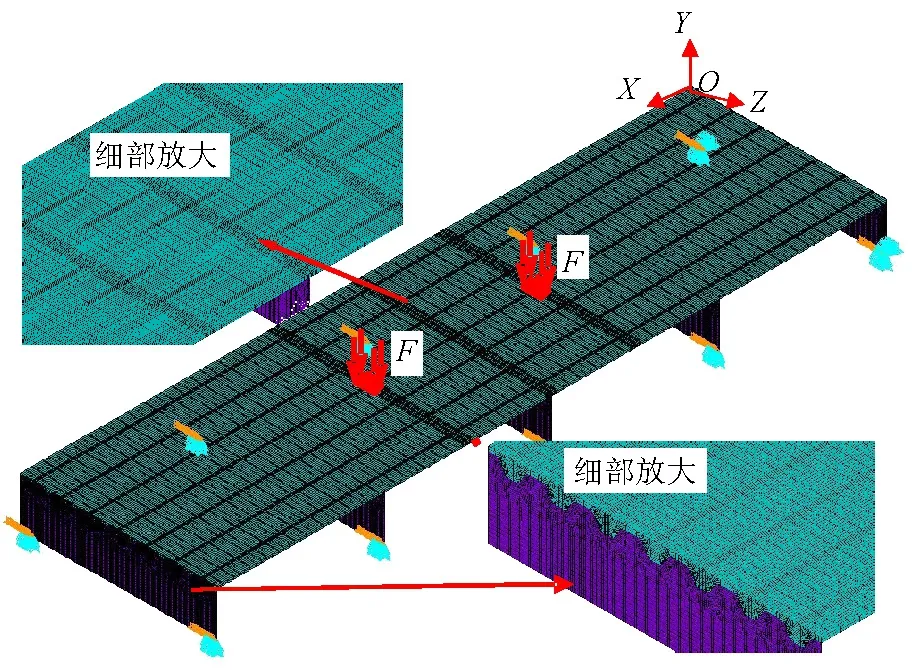
图3 结构的三维有限元分析模型Fig.3 3D finite-element model of subject under investigation
以多个重要受力部位的力学特性为考察对象,研究其对主要结构设计参数的影响效应.初步计算表明:UHPC结构层所受的压应力远小于其抗压强
度,因此不将其压应力作为考察指标;UHPC的抗拉强度远低于其抗压强度,将其作为主要考察指标;对于钢板而言,其拉压应力值均较大,且受各参数对其受力特性均有显著影响,也将其应力作为主要考察指标;此外在当前的约束条件下,各关注点的纵向(X方向)应力占较大比重,因此指标考察时以纵向(X方向)应力为主,各重要受力部位的具体考察位置如图2(b)所示,具体描述如表1所示.由于结构自重对于桥面板的适用性具有重要影响,研究中将纵向单位长度内的顶板结构自重也作为考察指标.各主要指标与设计参数间的相关关系规律如图4所示,为便于表述,拉压应力均取正值.

表1 考察点位置汇总表Tab.1 Inspection positions in the structure

(a) h1改变(b) b1改变(c) b2改变(d) b3改变图4 力学特性指标和关键参数间的关系Fig.4 Relationship between mechanical properties and key design parameters
根据已有文献[21-23]中波形组合桥面板尺寸和传统正交异性桥面板尺寸,拟定新型组合桥面板基准尺寸,h1、h2、b1、b2和b3取值分别为120、45、200、100 mm和200 mm,在此基础上进行单参数的影响效应分析,确定主要影响参数.普通正交异性钢桥面板主要采用Q345q,因此取其许用应力为172.5 MPa,UHPC许用拉应力参考文献[17]中无限寿命对应拉应力值为21.3 MPa.
由图4可知:
(1) 各关键位置的主要力学特性指标均随波纹钢板高度h1增大而减小,随后趋于平缓,表明结构的受力特性对该参数较为敏感.h1增大会增大桥面板结构的自重并影响其经济性和适用性,而过小的h1不利于组合销的安置,综合考虑应保持在100 mm左右;
(2) 钢板的拉压应力均随b1的增加显著下降,UHPC结构层的拉应力指标随b1的增大略有减小,表明钢板的受力性能对于该指标敏感,而UHPC结构层的受力特性对其不敏感,因此可将该取值范围限定在中间位置,此处为160 mm左右;
(3) 各力学特性指标均不随b2的增大而发生显著变化,表明结构的受力特性对该参数不敏感.但对于截面抗弯特性而言,在保持h1不变的条件下,斜段宽度越大,弯折角度越大,波形越平缓,截面抗弯刚度与截面面积之比越小,材料利用率越低.对于截面横向刚度连续性而言,斜段宽度越小,截面刚度过度越不平缓,即使在弯折处采用倒角处理,仍然会出现较大的应力集中,影响结构的其他性能.此外此参数的确定还需考虑板件加工制作的相关要求,后续研究中仍将该参数作为研究对象,也应将其值限定在中间水平,此处为110 mm附近;
(4) 钢板的拉压应力随波纹钢板顶部水平段宽度b3的增大而增大,位置2#处的混凝土拉应力随该参数增大而增大,位置3#处的混凝土拉应力则基本不随其变化,可在保证结构基本性能及构造要求的前提下,将b3取较小值,此处为110 mm左右;
(5)h1、b1、b2、b3均对结构的受力特性具有重要影响,是结构受力特性和优化设计研究的重要参数.综上所述,h1、b1、b2和b3的合理取值范围可以确定为80~120 mm、140~180 mm、80~140 mm和80~140 mm.
2 优化设计模型的建立
2.1 优化模型建立
采用评价函数法进行优化设计,常见的评价函数方法主要有理想点法、线性加权法、极大极小点法.此处采用理想点法[24],其思路为:
(1) 求出单一指标的最优解为
(1)
式中:X为n维向量;En为可行域;fi(X)为计算第i个考察指标的函数.
每一个研究对象所对应的考察指标值可集合成各自的点集F,F={f1,f2,…,fm}.
(2) 各考察指标很难同时达到最小值,采用欧氏距离度量F*与F间的偏差值,寻求偏差值的最小值作为最优解的近似解,得构造评价函数为
(2)

(3) 根据式(2)可得标优化模型为
(3)
以新型桥面板顶板结构为优化对象,以其结构设计参数h1、b1、b2和b3为设计变量,以已选定的力学特性指标和桥面板单位纵向长度自重指标W为目标值,建立新型桥面板的优化模型.
minφ(F)=
(4)
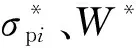
2.2 权重的确定
权重系数的确定是综合评价优化中的核心问题.确定权重的常用方法主要包括调查统计法、序列综合法、层次分析法和序关系分析法等.此处选用序关系分析法确定式(4)中的权重系数.序关系分析法较为成熟[24],此处只介绍其在该优化模型中的应用.
(1) 考虑到共有4个应力类指标和1个自重指标,两者与截面尺寸的关系大体上呈现截然相反的趋势,即使对指标数据进行归一化处理,自重指标也会因应力类指标较多而无法体现自身的重要性,故将自重指标反复计算4次并记为W1、W2、W3和W4后,再参与指标权重的计算.
(2) 由工程实际出发,降低结构自重是提高桥梁跨越能力、增强新型桥面板结构适用性的重要前提,相对于钢板的拉压受力而言,混凝土的抗拉性能应优先考虑;同时,钢板的受压状态应优于其受拉状态考虑,故各考察指标的重要性从大到小排序为[24]:W1、W2、W3、W4、σp2、σp3、σp4、σp1.
(3) 参照既有研究成果给出排序后相邻指标(xk-1与xk)重要性程度rk的判别值[24]:
(5)
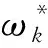
(4) 计算权重值,具体计算方法可参考文献[24],此处仅给出计算结果.

表2 相邻指标相对重要程度rk赋值表Tab.2 Reference table of rk valuation
将计算出的权重代入式(4),可得新型桥面板的优化模型,以确定新型桥面板的最优参数组合.
3 优化设计模型的BP神经网络方法
3.1 BP神经网络的建立
建立输入值(新型桥面板尺寸参数组合)和输出值(各考察指标)之间的函数关系,以确定各指标的理想点值,从而实现结构参数的优化设计.多参数的优化设计涉及大量参数组合,逐次考察每种组合效率较低,为此引入BP神经网络进行优化分析.该数学模型已经在函数逼近、模式识别、数据压缩等领域得到了广泛应用[25],其理论基础可参考文献[26],此处仅探讨该方法在新型桥面板结构设计优化中的应用问题.
采用Matlab进行BP神经网络的建模计算,建立典型的3层BP神经网络,输入维数为4,即输入4个设计变量值,输出维数为1,即输出1个目标值.根据神经网络中有关隐含层层数确定的经验理论,采用先以经验公式确定大致范围再试算选择最优的方式确定隐含层单元数为11,采用Sigmoid型可微函数作为隐含层的传递函数,采用纯线性函数Pureline为输出层的传递函数,采用带动量梯度下降的Traingdm改进型函数为训练函数.
选择合适的样本数据,分别训练出4个网络,建立起4个输入变量与每个考察点间的非线性映射的函数关系.由于自重具有简单明确的函数关系,只需单独计算而不参与BP神经网络的建模计算.
3.2 训练样本的抽取与处理
在1.2节中确定的h1、b1、b2和b3的合理取值范围内抽取样本,各参数的变化增量均取为 10 mm.所选取的训练样本遵循满布且均布所给取值范围的原则,均匀抽取样本144个,采用ANSYS参数化有限元模型的批处理机制获得样本数据.为使训练出的神经网络具有较好的推广能力,对所得样本数据进行归一化处理,输入值和输出值的归一化公式为
(6)
式中:a、b为常量,此处取a=0.1,b=0.8,将数据归一到0.1~0.9内;xmax和xmin为每组因子变量的最大值和最小值;xi为每组因子变量中的第i个因子变量;yi为xi归一化处理后的变量.
3.3 结构优化设计结果
在Matlab中调用训练好的4个BP神经网络,历遍计算所有参数组合下所对应的4个映射值,同时计算不同组合下的自重,分别得出5组考察指标结果值的最小值,并将其集合为理想点集合.将输入值、输出值和理想点集合均按式(6)归一化到0.1~0.9范围内.将所得的理想点集合与考察指标结果值代入单目标函数式(4),历遍计算求得函数最小值,此时的最小函数值所对应的截面参数组合即为所求的最优截面.单目标函数优化结果和与其相对应的截面参数值见表3,此处只列出前3组结果,其中第一个参数组合即为新结构所确定的最优结构设计参数.

表3 单目标优化结果Tab.3 Single objective optimal results
同时建模计算3个截面参数组合下的力学特性指标的有限元分析结果,并与BP神经网络计算值相比较,以证明所训练的BP神经网络的准确性,如表4 所示.结果表明,最大和最小误差分别为4.4%和-0.3%,满足工程要求,所提出的方法适用于波形顶板-UHPC组合桥面板的结构优化设计.

表4 拟合值与有限元值误差对照Tab.4 Comparison between fitted and finite element values
4 疲劳性能的初步研究
文献[16-19]指出UHPC结构层和组合销具备良好的疲劳性能,在车辆荷载作用下不会产生疲劳裂纹,因此此处考察波形顶板和横隔板部分的疲劳性能.建立有限元模型,选择跨中横隔板处的中间波段处的焊缝为关注对象,采用实体有限元模拟焊缝,如图5所示,整体有限元模型和约束条件和1.2节单参数影响分析相同,如图3所示.鉴于UHPC高性能混凝土具有优良的疲劳性能,故初步研究只关注钢结构部分可能的疲劳细节,考虑结构以及加载模式的对称性,主要有D1~D3 3个细节,如图5所示.国际焊接协会(IIW)按照式(7),分别提取距离焊趾0.4t和1.0t处的主应力(σ0.4t和
σ1.0t),再外推出焊趾处的热点应力σhs,其中t为板厚,此处顶板处厚为 8 mm,横隔板厚为14 mm.
σhs=1.67σ0.4t-0.67σ1.0t.
(7)
车轮荷载采用Eurocode中III级标准疲劳车辆荷载,车轮与桥面板接触面积为400 mm×400 mm,轴重为120 kN,横向轮胎中心间距为 2 m,轴距依次为1.2、6.0 m 和1.2 m,如图6所示.
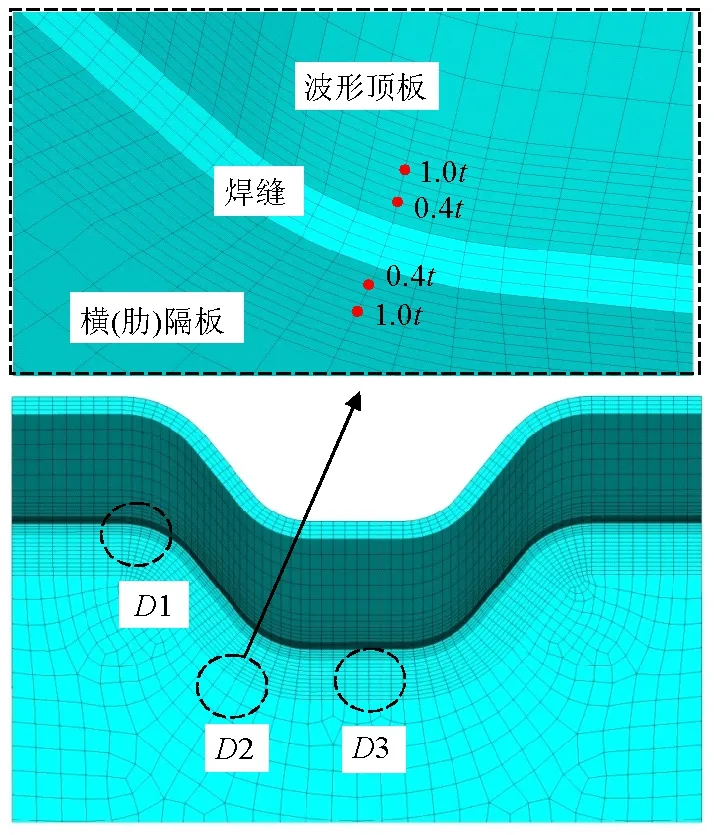
图5 关注的疲劳细节位置Fig.5 Location of the focused fatigue-prone detail

图6 标准疲劳车(单位:m)Fig.6 Standard fatigue load (unit: m)
取一个轮轴进行横向加载,确定纵向最不利位置.共有41个工况,D1~D3 3个疲劳细节的热点应力横向分布如图7所示.

(a) D1(b) D2(c) D3图7 关注的疲劳细节热点应力横向分布Fig.7 Transverse hot spot stress of focused fatigue-prone details
其中D2处顶板焊趾的应力最大,因此确定横向最不利加载位置为z=1.628 m.只考虑相距 1.2 m 的两个轮载荷载的影响,在横向最不利位置处进行纵向加载,D2的纵向应力如图8所示.
采用FAT90作为评价焊趾处热点应力疲劳强度的S-N曲线,FAT90级S-N曲线为200万次对应疲劳应力幅S为90 MPa,常幅疲劳极限为52.63 MPa,变幅疲劳截止限为33.2 MPa.根据Palmgren-Miner线性累积损伤理论进行疲劳寿命评估,计算损伤度D并估算结构疲劳寿命Y,计算结果如表5所示.偏于保守地将重车年通行量N取为5万次.
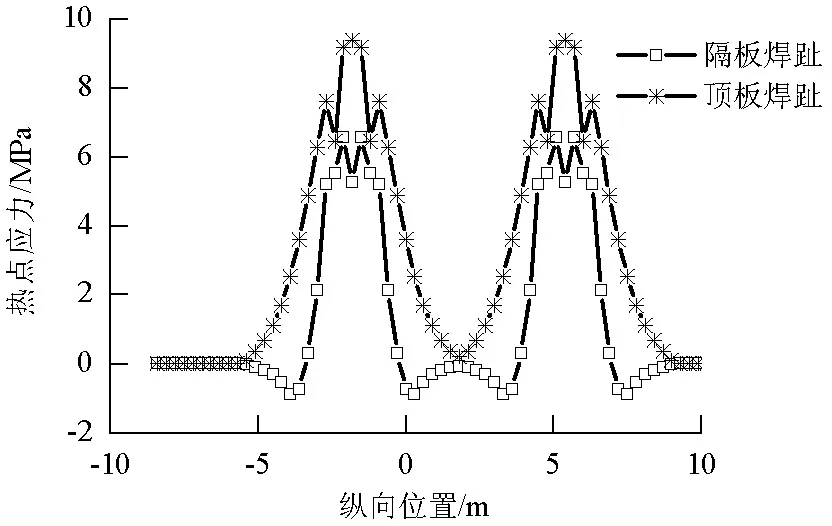
图8 D2疲劳细节热点应力历程Fig.8 Hot spot stress history of D2
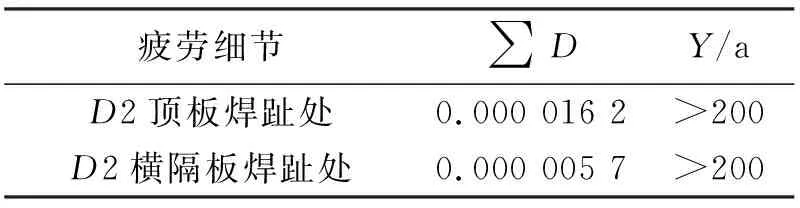
疲劳细节∑DY/aD2顶板焊趾处0.000 016 2>200D2横隔板焊趾处0.000 005 7>200
5 结 论
(1) 新型波形顶板-UHPC组合桥面板通过将波形顶板和UHPC结构层组成组合受力系统取代传统的纵肋和顶板受力体系,受力性能良好,能够显著减少焊缝和几何构型不连续部位数量并显著降低结构的应力集中程度,为正交异性钢桥面板的疲劳问题提供了较好的综合解决方案,是具有良好发展前景的桥面板结构;
(2) 波形钢板高度、波形钢板顶部和底部水平段宽度对于新型波形顶板-UHPC组合桥面板的受力性能具有重要影响,是其关键设计参数;波形钢板弯起部分的水平投影宽度是决定截面抗弯刚度和自重的设计参数;
(3) 基于BP神经网络的优化设计模型概念清晰,计算结果精度满足工程要求,适用于新型组合桥面板的结构优化设计;
(4) 当前的研究主要针对新型波形顶板-UHPC组合桥面板的受力特性和结构优化设计进行.同时对其疲劳性能的初步研究表明结构的疲劳性能优越.结构的静载破坏模式和极限承载力,疲劳失效模式和深入探究疲劳性能是下一阶段的研究重点.
