圆锥的（体积）变化

2018-07-12刘善娜

小学教学设计(数学) 2018年7期

关键词：草图直角圆锥

刘善娜

（作者单位：浙江宁波市奉化区实验小学）

【教学时机】

人教版六年级下册，圆锥的体积学习之后。

【教学过程】

一、回顾圆柱与圆锥的关系

1.看式子画图形。

看着 3.14×32×4÷3=37.68（平方厘米），请你描述一下这是一个怎样的圆锥？

2.请画出这个圆锥以及与它等底等高的圆柱的草图并标注相关数据。

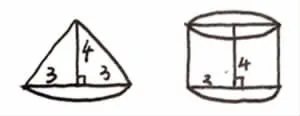
【设计意图：从式子想象图形，进一步掌握与圆锥体积计算相关的基本数据。】

二、三角形旋转，构成圆锥

1.要使三角形旋转形成圆锥，必须是什么三角形？以哪条边为轴旋转？

想象、描述、作图：直角三角形，一条直角边为轴，另一条直角边为底面半径。

师：以哪条边为轴，体积更大？为什么？

师：如果这个直角三角形的一条直角边为4，另一条直角边为3，试着求出这两个立体图形的体积。

小结：以较长的直角边为半径，得到的体积更大。

【设计意图：想象和描述是空间观念培养的主要途径，因此要多让学生经历想象、描述、作图的过程，并通过草图，掌握图形的特征。】

2.如果是以斜边为轴旋转，会形成什么图形？想象、描述、作图。

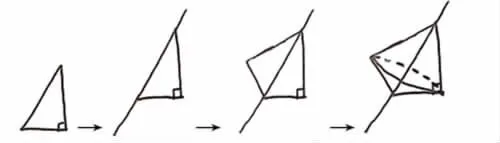
问1：这个直角三角形的一条直角边为4，一条直角边为3，则斜边为5，你能求出它的体积吗？

问2：能试着先确定思路吗？

画截面图，标注数据→尝试

讨论：先求半径，再设高为x和（5-x）。

（视学生解答情况进行引导）

小结：上下两个圆锥等底面，因此两部分的“高”可以融合。

【设计意图：以斜边为轴的立体图形的体积计算难度较大。但是拓展一下，有利于培养学生利用草图去分析的意识和能力。】

三、圆锥和圆柱的关系

1.画等底等高的一对圆锥与圆柱。

【设计意图：学生到了六年级，已经具备一定的分析能力，而且学生又有了三角形与平行四边形的变化经验，因此圆柱和圆锥的变化不再借助具体的数据，而是通过直观感知来确定“大小”。】

2.画等底等体积的一对圆锥与圆柱。

（1）学生尝试画。

（2）呈现正确作品，交流。

问：圆柱的高度，你是怎么确定的？

充分交流，多种思考角度：

①体积公式数据推理。

根据题意，可知Sh柱=Sh锥÷3→h柱=h锥÷3

（3）呈现画错的作品，引导学生自己分析错误。

【设计意图：确定圆柱的高度，对学生而言是比较难的。因此需要多角度帮助不同层次的学生理解“变化”。】

3.画等高等体积的一对圆锥与圆柱。

（2）学生上台展示，说理。

交流的核心问题：圆柱的底面大小，你是怎么确定的？

【设计意图：学生有了“确定高”的经验，“确定底面”教师就可以放手由学生来展示、说理，多角度表达自己的理解。】

4.跟进思考。

试着填一填“等（）等（），圆锥（）是圆柱的（）”。

小结：等底等高，圆锥体积是圆柱的三分之一；等底等体积，圆锥高是圆柱的三倍；等高等体积，圆锥底是圆柱的三倍。

追问：为什么后两种情况“等体积”时，作为“弱者”的圆锥的“高”和“底”，反而是圆柱的三倍了呢？

【设计意图：在学生的印象中，圆锥是“弱者”，他们会习惯于回答圆锥的（）是圆柱的三分之一。通过草图绘制，使学生从抽象的变化感知走向具体的大小感知。】

四、全课总结（略）

【教学建议】

等底等高的圆柱与圆锥的体积关系，学生不难掌握。但一旦逆向，如变成“等体积等高求底面积”的情况，学生就会混乱。在画图过程中，要把握好几个点：

一、掌握画图技巧：“底”和“高”能直接画，要先画好

“等高”“等底”是可以直接用草图表示出来的。如画一对“等底等体积”的圆柱和圆锥，等底，就先画两个小椭圆，很快能画好。但是“等体积”怎么画呢？学生会发现接下来要画的只能是“高”了，“底”配上“高”才有体积。画“体积”其实是一种间接的画，需要推算，要晚一步才能画，要让学生先有这样的基本认知。

二、重视错例分析：“体积”推算，多展示交流错误

如上所述画一对“等底等体积”的圆柱和圆锥，“画体积”相对较难，因此不仅要允许学生出错，还要呈现错例，分析对比。学生很可能在画出“等底”后又画了“等高”。画的时候，学生会出现混乱、画错高度，可一旦图形真的画出来后，他们也会发现这是“等底等高”，那“体积”一定是圆柱的大，能认识到自己画错了。毕竟学生对“尖尖的圆锥比较小，圆筒般的圆柱比较大”的直观感知是充分的。这是一种正向验证，也很有价值。