基于新息优先累积法的GM(0,N)模型及其应用

袁 泉，曾祥艳

（桂林电子科技大学 数学与计算科学学院，广西 桂林 541004）

0 引言

GM(0,N)模型考虑了多个相关因素对预测序列的影响，并且需要的样本数据量小，弥补了线性回归模型样本容量需求较大的不足，因此在预测和决策领域得到广泛应用[1,2]。GM(0,N)模型常用的参数估计法为最小二乘法[3]：通过误差平方和的最小化，寻找数据的最佳函数匹配，但是这种对误差的假设会造成预测模型的结构参数与估值之间的偏离或不一致。

1778年，意大利数学家P.Marchsi提出累积法：利用样本数据的加权累加直接估计模型参数，不需对误差进行假设，其几何意义是寻找样本点的一条重心线，能保证预测误差和趋于零[4]。累积法在经济计量和工程技术模型的结构参数估算中已经得到广泛应用[5-7]。李锋等已将累积法引入GM(0,N)模型中，提高了模型的预测精度[8]。但是普通累积法存在越老的数据占的权重越大，越新数据占的权重越小的问题，这与实际情况相悖，在现实中，新的信息对未来发展趋势的影响更大，所以，本文将基于新息优先的原则，改变累积法的累加顺序，使越新的数据占的权重越大，并将其引入GM(0,N)模型的参数估计中，提高模型的预测精度。

1 新息优先累积法

在实际情况中，预测需要更多地考虑最新的发展动态，新的信息对未来的影响大于旧的信息[9,10]。新息优先累积法就是基于越新的数据的权重越大，越老的数据的权重越小的原则。

设原始序列为：X={x1，x2，…，xn}，定义各阶新息优先累积和如下：

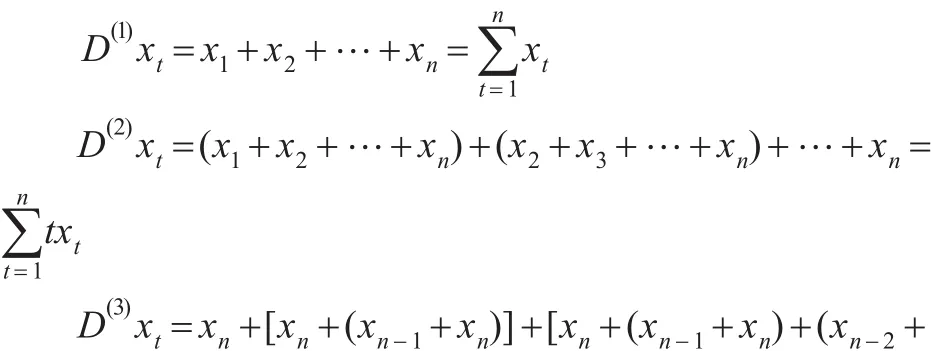
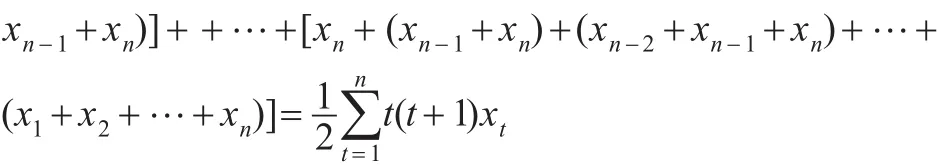
依此类推，对任意自然数r，有：

特别地，对序列长度为n的X={1，1，…，1}，称D(r)1为r阶基本新息优先累积和，其计算通式为：

2 基于新息优先累积法的GM(0,N)模型

GM(0,N)模型是变量导数阶数为0的静态灰色模型，基于原始数据的一次累加生成序列进行建模，一次累加生成可将非负序列生成为递增序列，从而增加序列的规律性。GM(0,N)模型含有多个变量，能反映多个相关因素对系统行为的影响。

对上述N个序列分别做一次累加生成（1-AGO）：

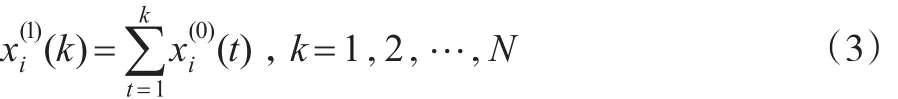
并设Xi(1)为Xi(0)的一次累加生成序列，即：

GM(0,N)模型的定义型方程为：

其中，a，b2，b3…，bN为模型参数。

下面，将新息优先累积法引入GM(0,N)模型的参数估计，假设新息优先累积算子的最高阶数为r，由GM(0,N)模型的参数有N个，因此r≥N，对GM(0,N)模型方程（4）两边施加1至r阶新息优先累积算子，得下列方程组：

其中：

则方程组可以写为矩阵形式：

对â的估计分为以下三种情况：

（1）若r=N，A是非奇异矩阵。此时A-1存在，参数估计式为：â=A-1Y；

（2）若r=N，A是奇异矩阵，且存在r＞N使得A是非奇异矩阵。此时取满足条件最小的r，参数估计为：

â=(ATA)-1ATY；

（3）若对任意r≥N，A均为奇异矩阵。此时更换原始数据的选取方式即可转换为情况（1）或情况（2）。

在实际应用中，一般A-1存在，所以，取r=N，参数a，b2，b3…，bN的估计为：

参数估计后，由基于新息优先累积法的GM(0,N)模型的定义型方程（4）即可得到系统行为特征数据序列的预测值

3 实例分析

3.1 实例一：水电发电量

取2009—2012年我国的年水电发电量作为模型的行为特征数据序列，相应年份的水电装机容量与国内生产总值作为模型的相关因素序列。相关数据见表1所示。其中国内生产总值水电发电量与国内生产总值的数据来源为《中国统计年鉴》，水电装机容量的数据来源为《全国电力工业统计数据》。

表1 2009—2012年我国的水电发电量及相关因素

原始数据包含一个系统行为特征数据序列与两个系统相关因素序列：

建立GM(0,3)模型：

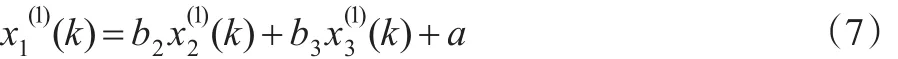
基于新息优先累积法估计模型参数有：

可得:

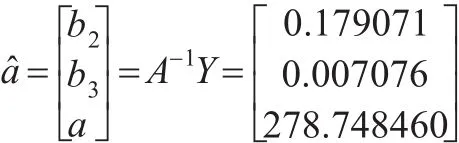
则模型的预测公式为：

由式（8）计算可得模型预测值，对2013—2015年我国水电发电量进行预测，并与基于最小二乘法和基于文献[9]给出的累积法建立的GM(0,3)模型的预测结果进行对比，见表2所示。

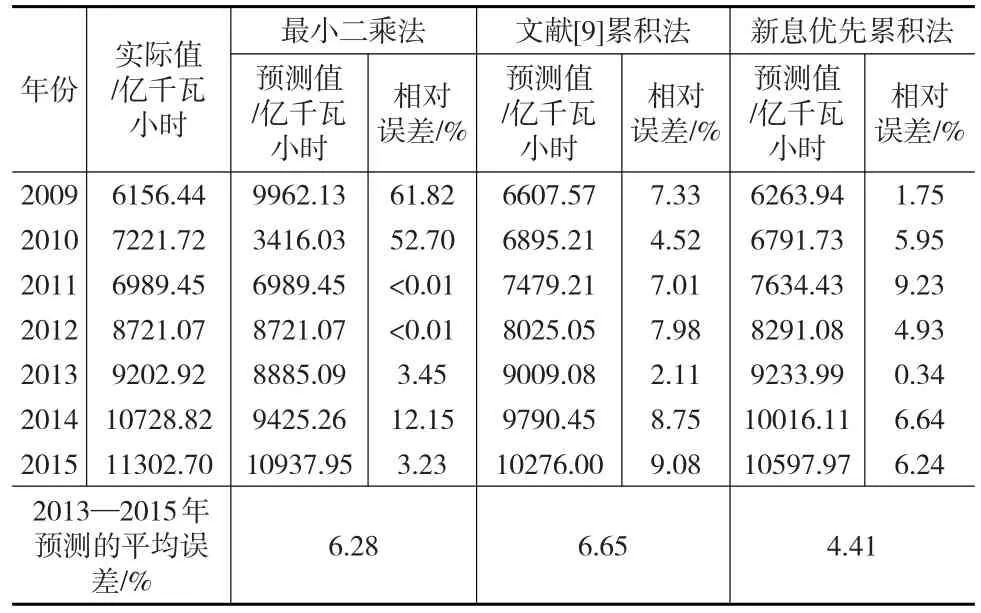
表2 三种参数估计法的GM(0,3)模型的预测结果比较

显然基于新息优先累积法的GM(0,3)模型的预测值更接近于实际值，预测精度更高。

3.2 实例二：社会消费品零售总额

取2008—2012年我国的社会消费品零售总额作为行为特征数据序列，选取国内生产总值、年末总人口与货币供应量这3个因素，作为模型的相关因素序列。相关数据见表3所示。数据来源为《中国统计年鉴》。

表3 2008—2012年我国的社会消费品零售总额及相关因素

建立基于新息优先累积法的GM(0,4)模型，模型的预测公式为：

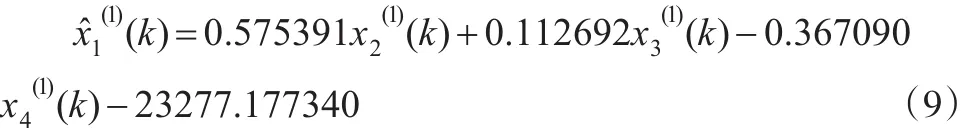
由式（9）计算得模型预测值，对2013—2015年我国的社会消费品零售总额进行预测，并与基于最小二乘法和文献[9]给出的累积法GM(0,4)模型的预测结果比较，见表4所示。

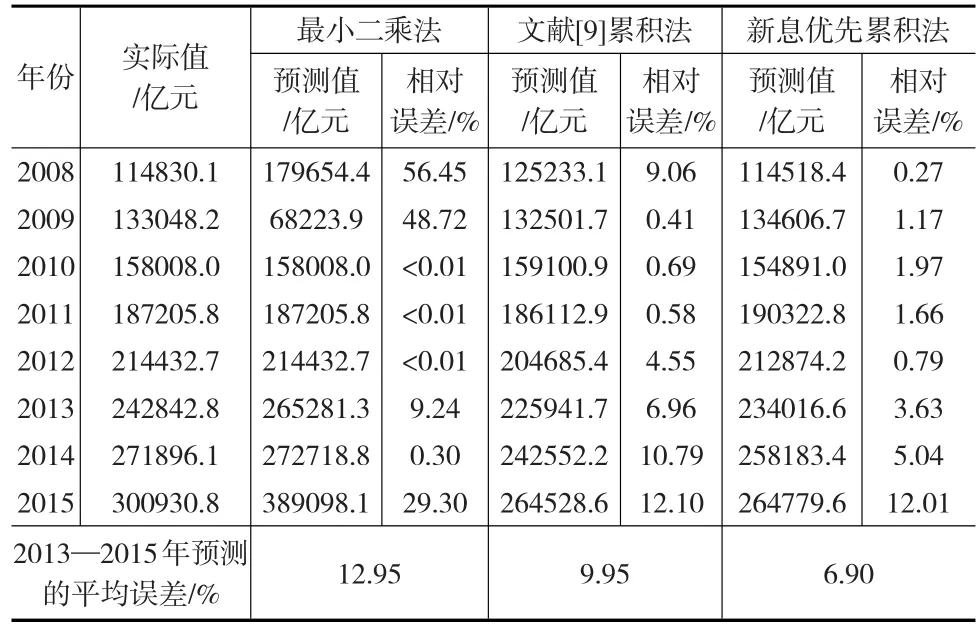
表4 三种参数估计法的GM(0,4)模型的预测结果比较

由表4可看出基于新息优先累积法的GM(0,4)模型的预测结果优于另两个模型，而且短期预测的精度更高。

4 结束语

本文改进了普通累积法，提出以越新的数据的权重越大为原则的新息优先累积法，并建立了基于新息优先累积法的GM(0,N)模型。两个实例验证的结果表明新息优先累积法GM(0,N)模型的预测精度相对于最小二乘法及普通累积法有了很大的提升。