基于F分布的最短置信区间研究

李广正

（中国人民银行兰州中心支行，兰州 730000）

0 引言

数理统计的本质是以样本推断总体，而区间估计又是统计推断的核心内容，所以研究区间估计问题具有重要意义。在给定置信水平的情况下，基于单峰对称分布的参数的区间估计，传统方法构造的区间是最短置信区间；当分布为单峰非对称时，利用传统方法构造的区间是等尾置信区间，而不是最短置信区间。

关于研究最优区间估计的文献有很多，李柏林[1]证明了最优区间估计的存在性，并推导出了常见分布的参数的区间估计公式；钱瑛[2]证明了单峰分布的最短置信区间的存在性；姜培华[3]证明了两正态总体方差比的最优区间的存在性，即F分布最优区间的存在性，这些文献都只是从理论上证明不同分布下的最优区间估计的存在性。徐晓岭[4]不仅运用拉格朗日乘数法证明了卡方分布的最优区间估计存在性问题，还利用matlab求解出了卡方分布最短区间估计值，并构造了不同自由度下卡方分布的最短区间估计用表。孙鹏哲[5,6]给出了F分布和卡方分布最短置信区间的左侧概率分配值表。其他针对单峰非对称分布的最优区间估计的研究还有很多，例如，王学敏[7]研究了指数分布和瑞利分布参数的最短区间估计问题。本文根据以上文献的研究思路，研究如何计算出F分布最短区间估计用表，力争在精度上优于传统方法。

1 基于两正态总体方差比的最短区间估计

设x1，x2，…，xm是来自正态分布的样本，y1，y2，…，yn是来自正态分布的样本，且两样本相互独立。两样本均值分别为和两样本方差分别为：

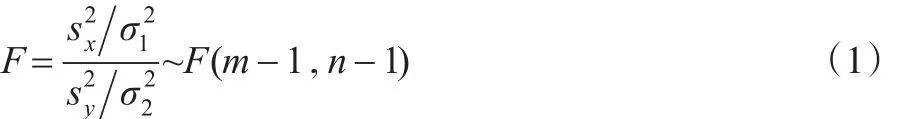
对给定的置信水平1-α，由：

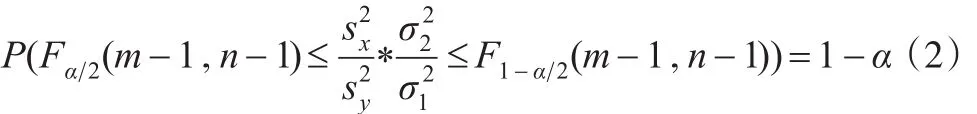
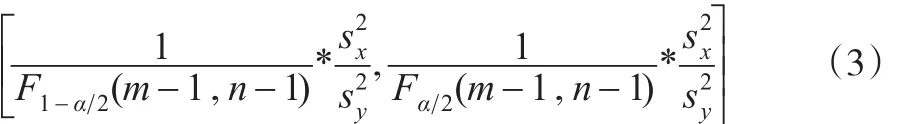
对给定的置信水平1-α，取满足条件：

的x1和x2。由此得到的1-α的最短置信区间：

其中，0＜x1＜x2，且满足：

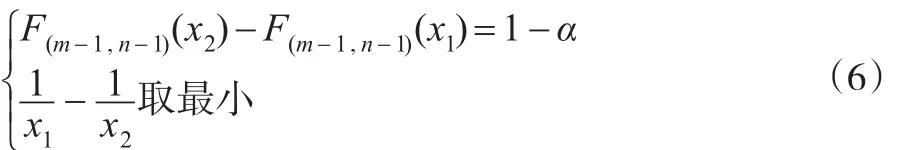
F(m-1，n-1)(x)为F(m-1，n-1)的分布函数 。

姜培华[3]证明了基于F分布的两正态总体方差比的最优区间估计的存在性及唯一性，即上述非线性规划问题存在最优解。

周岱翰强调，饮食要均衡。一年到头，他雷打不动要吃的“宝贝”，是最平常不过的苹果，每天1～2个。有人问他：“苹果就那么好吃吗，吃多了不厌烦吗？”“苹果如果不好吃，就当药吃嘛！”他说。

作者简介：李广正（1990—），男，河南信阳人，硕士，助理经济师，研究方向：商务统计。

2 最优置信区间的程序实现

孙鹏哲[5]运用数值模拟方法，利用R软件计算最短置信区间对应的左侧概率分配值，同时给出了最优左侧概率分配统计表。其计算步骤为：第一步，计算基于最短置信区间对应的左侧概率分配值；第二步，计算由第一步得到的左侧概率分配值对应的分位数，此分位数就是最优区间的左侧端点值，再计算右侧概率分配值对应的分位数，即为最优区间的右侧端点值。由于每一步的计算结果都不是精确的解析解，而是近似的数值解，所以这种分两步计算最优区间估计的方法扩大了估计误差。而且，该文章只给出了基于F分布下最优左侧概率分配统计表，必须通过此表再计算相应概率下对应的分位数，才能得到最优区间估计，这给实际应用带来了麻烦。基于这种考虑，本文通过运用拉格朗日乘数法，利用mathematics软件分别计算出了在0.9、0.95和0.99置信水平下基于F分布的最短置信区间，并构造了F分布的最短区间估计用表。

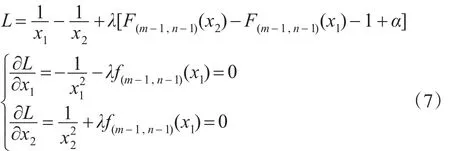
由式（2）得：

由于F分布的分布函数形式非常复杂，一般的软件很难求出式（6）决定的非线性规划问题的最优解。本文通过运用拉格朗日乘数法，将一个求解非线性规划问题转换成求解方程组的问题。经过分析可知，由式（6）决定的非线性规划问题的最优解和由式（4）和式（8）组成的方程组的解相同。利用mathematics软件里的FindRoot函数能较精确地求出方程组的近似根。对于F(m，n)分布，只有当n＞4时，分布的方差才存在，故为保证方差存在，本文的最优区间估计表是在两个自由度都大于4的条件下计算的，具体程序略。

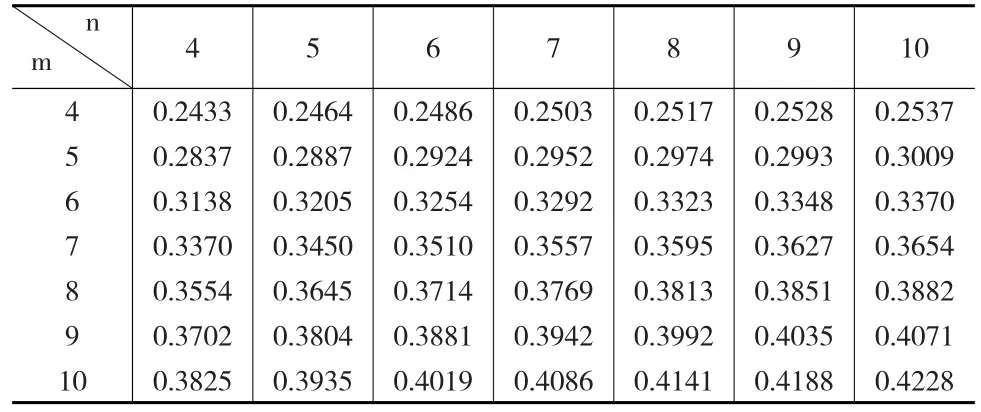
表1 0.9置信水平下最优区间的左侧端点值

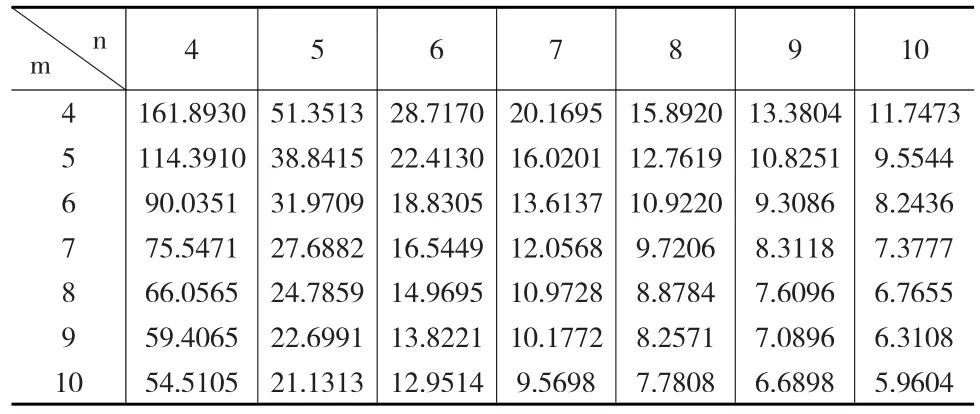
表2 0.9置信水平下最优区间的右侧端点值

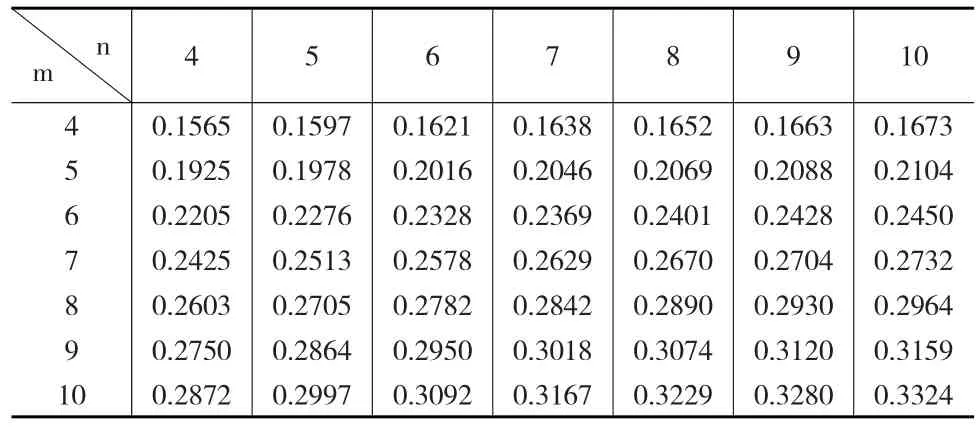
表3 0.95置信水平下最优区间的左侧端点值

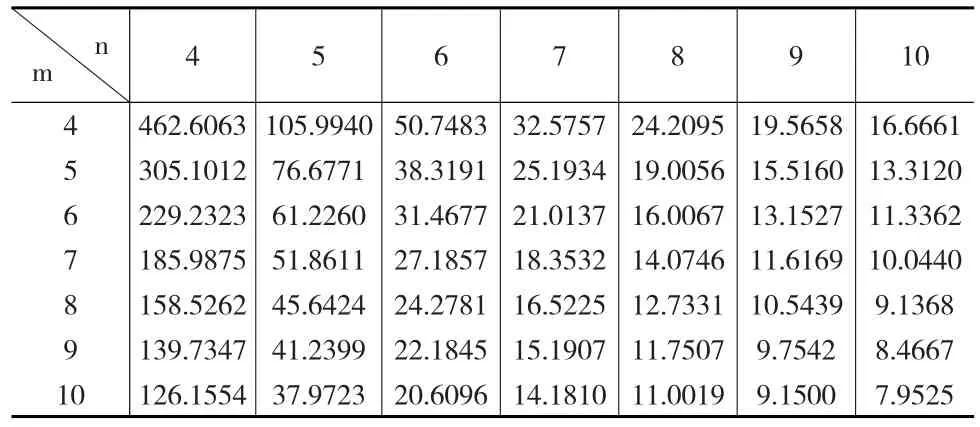
表4 0.95置信水平下最优区间的右侧端点值

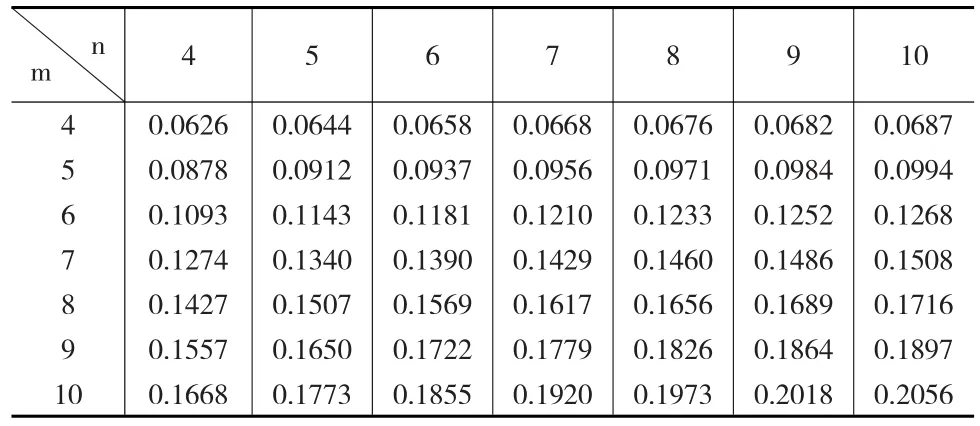
表5 0.99置信水平下最优区间的左侧端点值

表6 0.99置信水平下最优区间的右侧端点值

3 结论

本文计算出了在0.9、0.95和0.99置信水平下基于F分布的最短置信区间，构造了最短区间估计用表，同时将本文的方法与传统方法和文献[5]中介绍的方法进行比较，比较结果见表7。在表7中，区间长度1表示使用本文方法构造的最短置信区间的长度，区间长度2表示使用文献[5]的方法构造的最短置信区间的长度，等尾置信区间长度表示传统方法构造的置信区间的长度。（注：此处的区间长度比实际的区间长度少了倍，表7中的区间长度比是区间长度1与等尾置信区间长度的比值）。

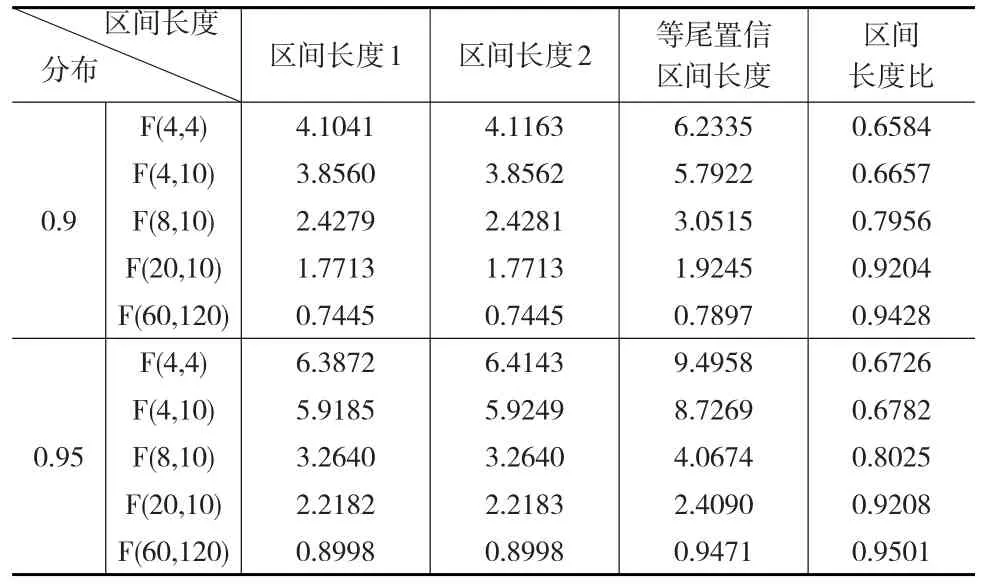
表7 不同方法构造的置信区间对比

从表7中可以看出，在给定置信水平情况下，三种方法求得的置信区间长度都是随着F分布的自由度的增加而减少，这是由于F分布随着自由度的增加，其密度函数呈现“尖峰薄尾”的形状，样本的集中趋势越来越明显。

通过对比可以看出，在给定置信水平和自由度情况下，本文计算的最短置信区间要优于文献[5]中计算的置信区间，且两者都远远优于传统方法构造的置信区间。而且，三个置信区间之间的差别随着自由度大小的不同存在一定的变化。例如，在0.9置信水平下，当F分布的两个自由度为4，4时，区间长度1为4.1041，区间长度2为4.1163，区间长度1略优于区间长度2；当F分布的自由度为20，10时，两者的区间长度几乎一样。在0.9置信水平下，当F分布的两个自由度为4，4时，区间长度1为等尾置信区间长度的65.84%；当F分布的自由度为20，10时，区间长度1为等尾置信区间长度的92.04%，两者之间的差别在缩小，这是由于当F分布的自由度增加时，其密度函数的对称性越来越明显，区间长度1与等尾置信区间的长度也越来越接近。所以，在小样本情况下，研究F分布的最短区间估计是有意义的。

相比于文献[5]中的方法，本文的方法一方面在精度上优于前者（在小样本情况下比较明显），另一方面在使用便利程度上也优于前者。本文直接构造了F分布的最短置信区间估计用表，而文献[5]只给出了F分布的最短置信区间的左侧概率分配值表。

相比于传统方法，本文的方法不仅在精度上要远远优于传统方法，而且在适用面上也要比传统方法更广泛。使用传统方法构造等尾置信区间时，需要查阅F分布的分位数表，而一般教材提供的都是有限自由度下F分布的分位数表，本文介绍的方法在理论上可以计算任意自由度下的F分布的最短置信区间，所以其适用面更广。