基于GIOWHA算子的汇率组合预测模型

丁小松，杨桂元

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000）

0 引言

过去对目标序列的预测都是借助于单项预测方法进行，但单项预测方法只利用了研究对象局部的有效信息，未能实现对研究对象整体信息的综合利用，不能确保预测在所有的时点都具有较高的精度。为改变传统预测方法的片面性，提高预测的精度，Granger和Bates（1969）提出了组合预测方法：通过赋予多种单项预测方法不同的权重，基于一定的优化准则，求解最优权重，实现对不同单项预测方法预测信息的充分利用，解决了单项预测的片面性，达到优于单项预测的效果。

过去的文献主要有两个研究方向：组合预测（点预测）和区间组合预测（区间预测）。如文献[1]利用IOWHA算子组合预测模型对房地产价格进行预测，文献[2]利用IGOWLA算子对区间序列构建组合预测模型进行区间预测，其实质为两次点预测，即对区间左右端点进行预测，构成区间预测。而对组合预测模型研究的思路主要有两种：一是直接研究预测值和实际值的拟合程度，具体方法有相关系数法、向量夹角余弦法等。如文献[3]以实际区间半径和区间中点与预测区间半径和区间中点之间的相关系数最大为准则，构建多目标组合预测模型。文献[4]则以实际值和预测值间的向量夹角余弦最大为准则求解组合预测模型中的权重。二是研究实际值和预测值之差即误差项，方法有误差平方和最小、误差绝对值之和最小、最大偏差最小、贴近度最大、灰关联度最大及Theil不等系数法等。如文献[5]以实际序列和预测序列直接的贴近度为优化目标求解组合预测模型的权重，而文献[6]则以灰关联度最大为准则求解组合预测模型的最优权系数。

本文利用广义诱导有序加权调和平均算子构建组合预测模型，以实际序列和预测序列的p次幂倒数误差的平方和最小为准则，求解组合预测模型的权重向量，并以预测人民币汇率序列说明所构建模型的预测效果。

1 相关概念及符号说明

设某序列第t期的实际观测值为xt，共有n种单项预测方法，第i种预测方法第t期的预测值为xit，第i种方法第t期的预测误差为eit，x̂t为第t期的组合预测值，et为第t期的组合预测的误差。其中i=1，2，…,n，t=1，2，…，N。

定义1：设OWAW:Rn→R为n元函数，W=(w1，w2，…，是和OWAW相关的权重向量，且ii=1，2，…，n。则称：

为n维有序加权算术平均算子，简称OWA算子，其中bi是 (a1，a2，…，an)由大到小排列的第i个数值。

定义 2：设 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)为 n 个二维数组，W=(w1，w2，…，wn)T为权重向量，且0≤wi≤1，i=1，2，…，n。则称：

为n维诱导有序加权算术平均算子，简称IOWA算子。其中，v-index(i)是 (v1，v2，…，vn)（诱导变量）由大到小排列的第i大数的下标。

定义 3：设 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)为 n 个二维数组，W=(w1，w2，…，wn)T为权重向量，且≤wi≤1，i=1，2，…，n。则称：

为n维诱导有序加权调和平均算子，简称IOWHA算子。其中，v-index(i)是 (v1，v2，…，vn)（诱导变量）由大到小排列的第i大数的下标。

定义 4：设 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)为 n 个二维数组，GIOWHAW:Rn→R为n元函数，W=(w1，w2，…，wn)T为权重向量，且则称：

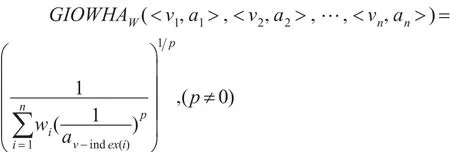
为n维广义诱导有序加权调和平均算子，简称GIOWHA 算子。其中，v-index(i)是 (v1，v2，…，vn)（诱导变量）由大到小排列的第i大数的下标。

当p=1时，GIOWHA算子退化为诱导有序加权调和平均算子IOWHA；当p=-1时GIOWHA算子退化为诱导有序加权算术平均算子IOWA；当p→0时GIOWHA算子退化为诱导有序加权几何平均算子IOWGA；当p→+∞时GIOWHA算子退化为min{ }a1，a2，…，an。（证明略）

2 基于GIOWHA算子的最优组合预测模型

为第i种方法第t期的预测精度，其中vit∈[0，1]。以vit为诱导序列与各单项预测方法在t时刻的预测值相结合，可得 n 个二维数组 (＜v1t，x1t＞， ＜v1t，x2t＞，…， ＜vnt，xnt＞)，t=1，2，…，N。

定义6：令

的有序加权调和平均组合预测值，简称GIOWHA算子组合预测值。为诱导有序p次幂倒数误差，i=1，2，…，n，t=1，2，…，N，则广义诱导有序加权调和平均组合预测的p次幂倒数误差为：

易知，GIOWHA算子根据不同时刻各单项预测方法的不同精度赋予不同的权重。以下使用p次幂倒数误差度量组合预测方法的有效性。

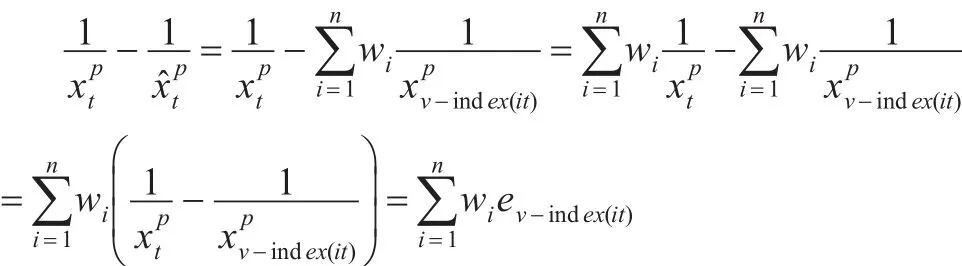
于是广义诱导有序加权调和平均组合N期的组合预测p次幂倒数误差平方和为：

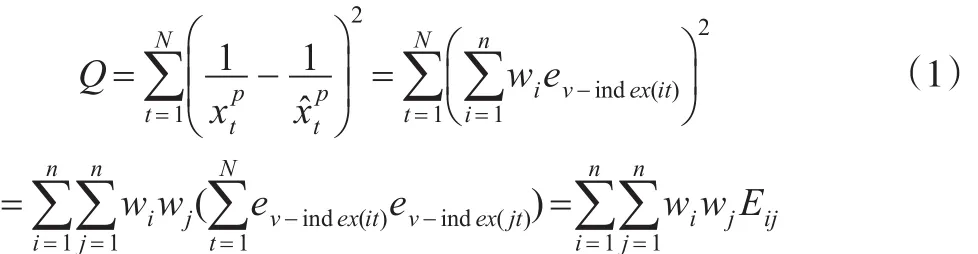
则基于误差平方和最小的GIOWHA组合预测优化模型形式如下：

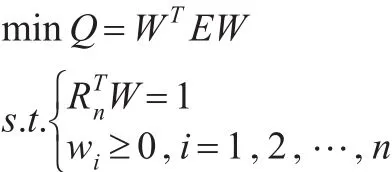
其中Rn=(1，1，…，1)T是分量均为1的n维列向量。

3 实例验证

本文以2006年1月至2016年8月的人民币汇率（直接标价法：一美元折合人民币数）期末值为样本，其中2006年1月至2016年2月的数据用于估计自回归模型、多项式回归模型以及局部多项式回归模型，而2016年3月至8月的汇率数据用于验证各单项预测模型与组合预测模型的预测效果，这样做既考虑了内插预测误差，又考虑了外推预测误差，前者为模型内误差，后者为模型外误差。数据源于中国人民银行官网。

图1 2006.1—2016.8人民币兑美元汇率时序图

由图1可知，人民币汇率从2006年1月开始不断升值，直至2015年7月开始贬值。

3.1 模型一（自回归模型：AR（p））

自回归模型的形式为：

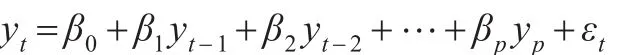
通过构建AR（1）、AR（2）和AR（3）可知AR（2）的估计结果最优，结果如式（2）：

其中yt为即期汇率，yt-1，yt-2为汇率的滞后项，括号内的数值为估计参数的t值。

对残差项序列相关性检验结果如表1所示，所估计的AR（2）模型的残差项不存在序列相关性。

表1 LM检验

对残差项进行ARCH效应检验即异方差检验结果如表2所示，所估计的AR（2）模型的残差项无异方差性。

表2 ARCH效应检验

由表1和表2可知，AR（2）模型对汇率数据有很好的拟合效果，故使用AR（2）进行2016.3—2016.8的静态预测，结果如表3所示：

表3 AR（2）模型预测结果

3.2 模型二（ETS指数平滑状态空间模型）

Pegel（1969）首先对指数平滑方法进行了分类，随后Gardner（1985）对其进行了拓展，Hyndman等（2002）进行了修正，最后又被Taylor（2003）改进。

手术室护理始终是护理工作的研究热点,因手术室护理质量直接关乎患者生命健康,尤其是手术实施过程中,任何手术失误会影响手术效果、预后效果,不仅会增加患者的住院时间,增加患者经济负担,还会增加医生、患者的精神压力,引发医患纠纷[3]。因此提升手术室护理,规避风险,提高手术室质量,具有重要意义。

本文使用加性模型，故可对时间序列做如下分解：

yt=Tt+St+Ct+εt

其中，T为长期趋势，S为季节效应，C为循环变动，ε为不规则变动。ETS指数平滑状态空间模型（以下简称ETS模型）中的E为误差项、T为趋势项、S为季节效应。E可以是加性的（A），也可以是乘性的（M），同时T和S可以是加性的（A）、乘性的（M）或者不存在（N），其中T可以细分为衰减加性（dampened additively简称Ad）或者衰减乘性（dampened multiplica-tively简称Md）。因此，指数平滑法一共有30种组合，包括线性的和非线性的，但只有15种具有乘性误差项的可用于时间序列分析。

加性误差模型：ETS（A，Ad，N）

令ŷt=lt-1+bt-1表示yt的一步向前预测，εt=yt-ŷt表示t时刻的预测误差，假定所有参数已知。则空间状态模型为：

令αβ*=β，则式（5）可被简化。由于式（3）至式（5）均包含误差项εt，因此也被称为新息状态空间模型。

为得到空间状态模型的标准形式，令xt=(lt，bt)T，将式（4）和式（5）带入式（3）得：

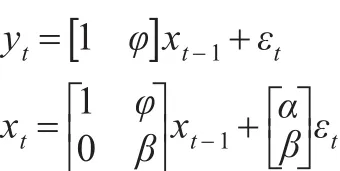
当εt的分布已知时，上述标准化的模型被完全识别，通常假定εt是独立同分布的，即εt～N(0，σ2)。本文的ETS（A，Ad，N）模型中存在加性误差项，衰减加性趋势项，无季节效应。模型的估计结果如表4所示：

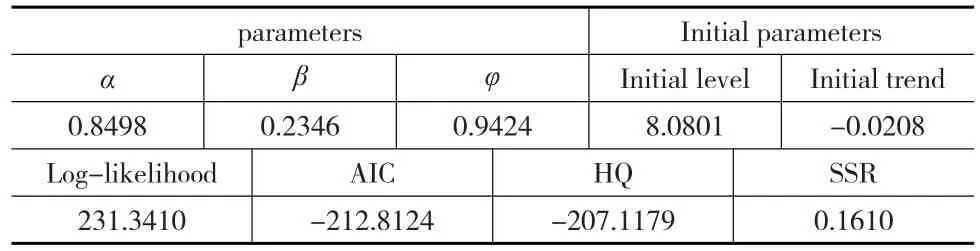
表4 ETS（A，Ad，N）模型估计结果

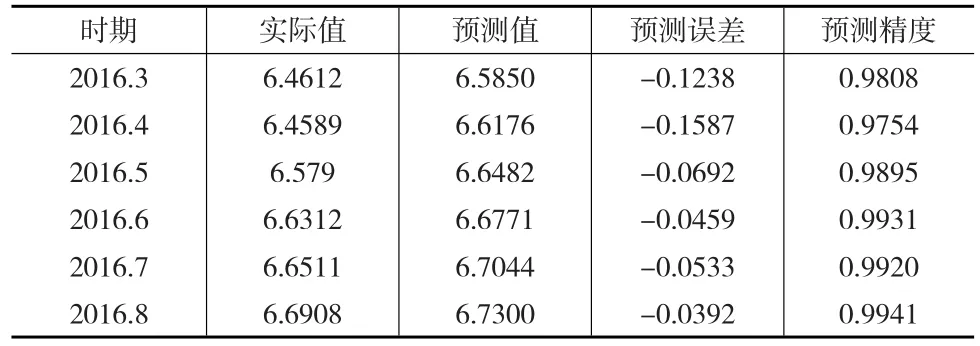
表5 ETS模型预测结果

3.3 模型三（局部多项式回归）

非参数回归中不需要对数据的生成过程做出具体的假定，其模型的形式通常为：

其中，m(x)为解释变量的函数，e为模型的误差项。

局部多项式估计的原理是使用多项式逼近m(x)。设m(x)在X=t处的p+1阶导数存在，x为t邻域内的任意一点，则m(x)的Taylor展开式为：

式（7）中m(p)(t)为m(x)在t处的p阶导数，可视为待估参数，则式（7）可化为：

m(x)≈β0+β1(Xi-t)+β2(Xi-t)2+…+βp(Xi-t)p（8）

式（8）可由广义最小二乘法进行估计，即最小化目标函数：

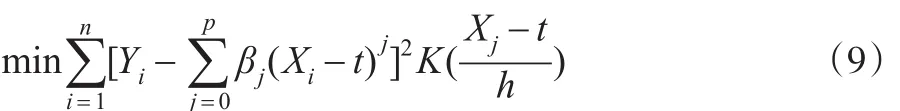
式（9）中 (X1，Y1)，(X2，Y2)，…，(Xn，Yn)为 (X，Y)的观测样本为权函数。本文选择核函数epan2为权函数，拟合效果如图2所示。

图2 局部多项式拟合图

当预测期数超过6期时，局部多项式回归的拟合精度急剧下降，所以只进行6期预测，其预测结果如表6所示：

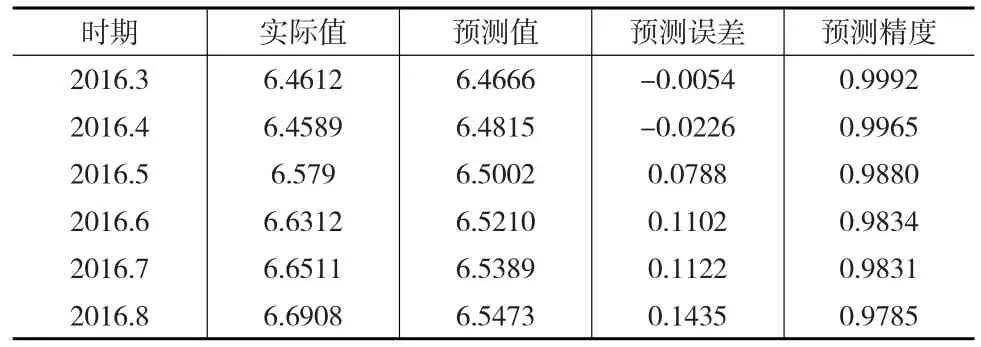
表6 局部多项式回归模型结果

3.4 基于GIOWHA算子的组合预测模型

为对组合预测模型的有效性进行评，构建如下评价指标体系：

（3）均方百分比误差

根据本文的三种单项预测方法在各时点的预测精度为诱导序列，对其在各时点的预测值进行诱导，则可以得到t时刻预测精度和预测值构成的二维数组：＜v1t，x1t＞，＜v2t，x2t＞，…，＜vnt，xnt＞ 。

当p=1时由定义（6）可计算GIOWHA组合预测值，其计算过程为：

（5）均方误差

将上述结果带入式（1），整理得如下模型：

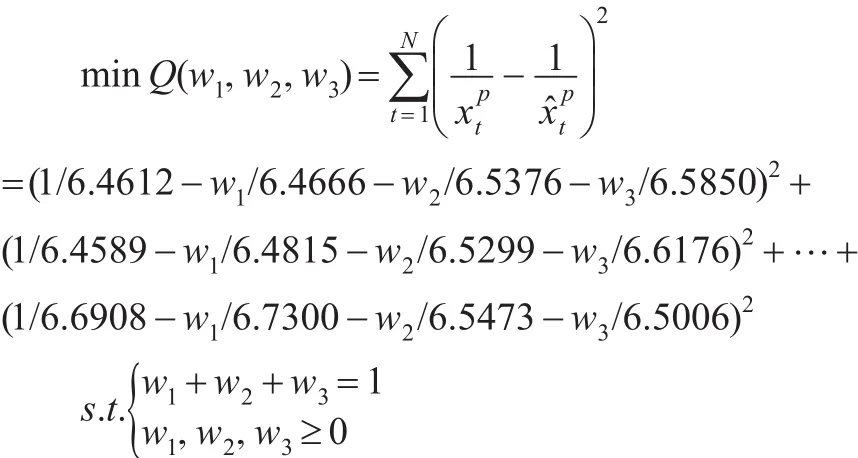
表7 基于GIOWHA算子的组合预测结果

为验证GIOWHA组合预测模型的有效性，计算上述5项评价指标，结果如表8所示：

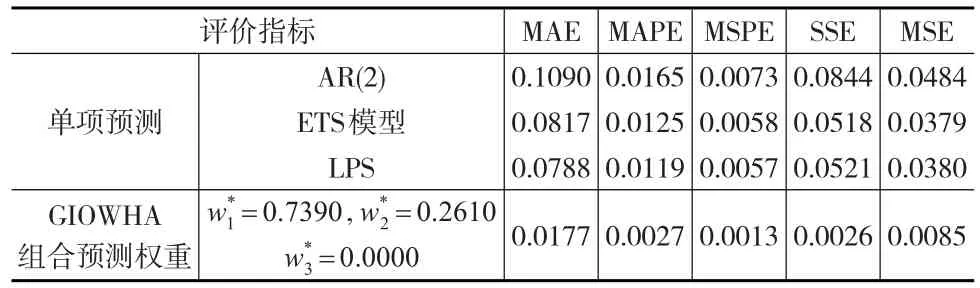
表8 单项模型和组合预测模型的外推误差

由表8可知GIOWHA组合预测模型各项指标均优于单项预测方法，因此可初步得出其可改善预测精度的结论。

由表8计算的各种误差指标为外推误差，即模型外误差，为充分评价组合预测模型的预测有效性，计算其模型内误差，即内插误差如表9所示：

表9 单项预测模型与组合预测模型的内插误差

由表9可知GIOWHA组合预测模型的内插误差与各单项预测方法相比同样是最小的，因此，与各单项预测方法相比，本文构建的基于GIOWHA的组合预测模型在内插误差和外推误差中均具有更优秀的表现。

4 结束语

本文以2006年1月至2016年8月人民币汇率为研究对象，利用三种单项预测方法：自回归模型、ETS指数平滑状态空间模型和局部多项式回归模型对汇率数据进行拟合预测。数据集被分为两个部分，用2006年1月至2016年2月的数据估计模型，而2016年3月至2016年8月的数据则用于验证模型的外推预测效果。然后建立基于诱导有序加权几何平均算子（GIOWHA）的组合预测模型，以p次幂倒数误差平方和最小为准则求得最优权重。最后利用多项评价指标对各模型的预测效果进行评价，发现基于GIOWHA的组合预测模型的模型内误差和模型外误差均优于三种单项预测模型，可以对汇率序列做出更精准的预测。