含夹层盐岩椭球储气库极限压力
2018-07-12陈金平贾善坡张雪松井文君
陈金平, 贾善坡, 张雪松, 井文君, 龚 俊
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.长江大学城市建设学院,湖北荆州 434023)
地下盐岩储气库能够较好地解决城市用气不均匀性问题,起到季节性调峰作用,同时在输气系统或气源故障导致输气中断时用以保证连续供气,与其他调峰方式相比,地下盐岩储气库储备能力大、范围广[1]。中国地下盐岩储气库中考虑到腔体稳定性及造腔工艺,腔体形状大多设计为椭球形,椭球形储气库相对其他类型储气库具有储存量大、安全性高、经济等特点。在地下储气库稳定性研究和合理运行压力确定过程中,储气库腔体形状的变化对腔体的稳定性有重要影响,合理的形状参数有助于提高储气库的极限压力,给运行压力的确定提供合理的选择范围,确保储气库腔体的稳定性和安全性。郤保平等[2]运用弹塑性模型数值模拟方法得出运行气压为8~24 MPa时,储气库为椭球腔,且长短轴比为7/4时结构最稳定;Zimmels等[3]使用FLAC软件计算了圆形洞室在不同水平构造应力、内压和洞室间距时围岩的塑性区,确定了最佳运行内压及洞室间距;Stenven等[4]分析不同腔体形状、不同腔体直径的储气库盐岩损伤安全指数变化情况,并建立盐岩损伤安全指数与腔体尺寸关系;夏才初等[5]针对压气储能地下洞室方案选型和密闭性要求选择了典型的洞室埋深,考虑不同的洞室形式和尺寸,采用ABAQUS有限元软件模拟充气后围岩的受力和变形特征,获得合适的洞室形式;王同涛[6]针对4种方案盐穴储气库尺寸利用FLAC3D有限元软件建立了国内某多夹层盐穴储气库的三维数值计算模型,对计算结果进行对比并优选出最佳方案;王保群[7]讨论了不同腔体形状对盐岩损伤、体积收敛、密闭性、地面沉降的影响,总结出中国薄层盐岩储气库的较适宜形状;许宏发等[8]利用弹性理论应力叠加原理求得在地应力场和内压作用下储气库腔壁上关键点的应力解析解;时文等[9]针对3种形态的盐穴储气库模型在变化的运行压力下分析腔壁应力分布和腔体体积变化,得到储气库稳定的影响因素。关于层状盐岩中储气库运行压力的研究大多集中在确定长期注采气循环压力下腔体蠕变收缩和腔体密闭性控制的合理运行压力方面,而对腔体长短轴之比变化时,储气库极限压力研究较少。显然,不同储气库模型形状及尺寸直接影响储气库的极限压力及安全性。笔者利用ABAQUS有限元软件自带修正的Mohr-Coulomb模型分析在地应力场和内压作用下,不同长短轴之比椭球形储气库腔体在极限压力作用下的破坏情况,比较储气库腔体在不同长短轴之比下极限压力差别和夹层的破坏情况,研究最佳椭球形储气库变形及破坏规律。
1 修正的Mohr-Coulomb破坏准则
一般应力状态下剪切型Mohr-Coulomb屈服准则可由3个应力不变量表示,其方程式为
F=Rmcq-ptanφ-c=0,
(1)
其中
tanφ,
S=σ+pΙ.
式中,c为岩石黏聚力,MPa;φ为岩石内摩擦角,rad;p为静水压力,MPa;q为Mises应力,MPa;S为偏应力,MPa;Ι为单位阵;σ为应力张量,MPa;Θ为极偏角,rad。
以应力不变量表示的拉伸型Mohr-Coulomb屈服准则为
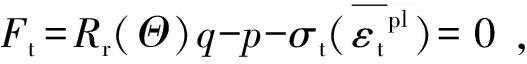
(2)
其中
Rr(Θ)=(2/3)cosΘ.
在π平面中剪切型Mohr-Coulomb屈服函数是一个不等角的六边形,主应力空间屈服面由3个分别垂直于主应力轴的平面组成,且在主应力空间为一个棱锥面,中心轴线与等倾线重合。在子午面上复合Mohr-Coulomb屈服准则的轨迹如图1所示。

图1 在子午面上的复合Mohr-Coulomb屈服准则Fig.1 Complex Mohr-Coulomb yield criterion in meridional plane
采用双曲线方程对拉伸型和剪切型Mohr-Coulomb屈服准则进行拟合,如图2所示。屈服函数表达式与势函数的表达式一致。通过调整初始黏聚力与子午面上偏心率乘积εc0来反映岩土介质的抗拉强度,在ABAQUS软件中,ε为子午面上偏心率,默认值为0.1,c0为初始黏聚力,默认值为0,通过调整该乘积拟合复合曲线。
修正的Mohr-Coulomb塑性势函数与修正的屈服准则表达式分别为
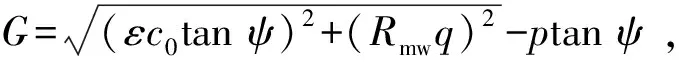
(3)
(4)
其中
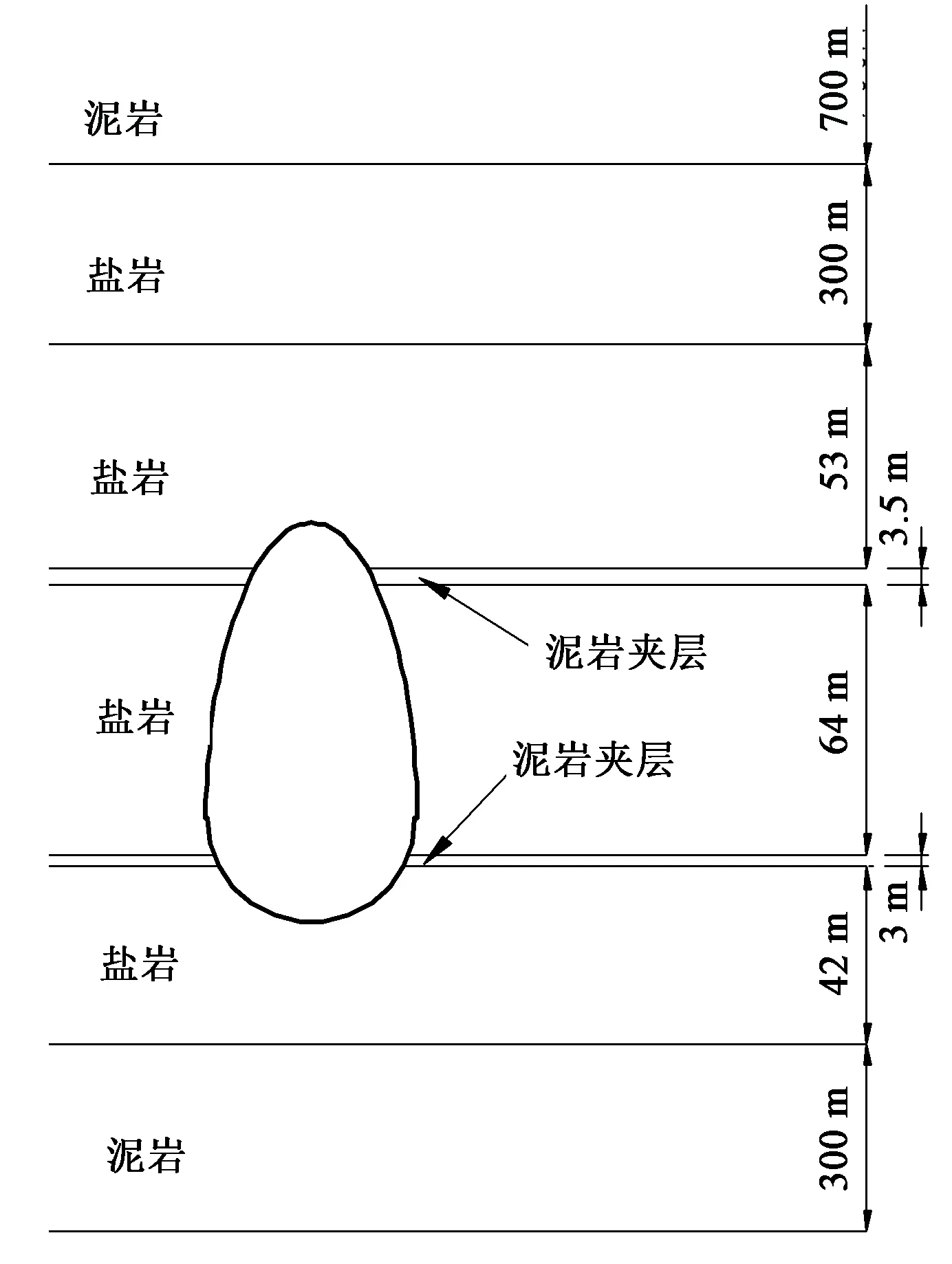
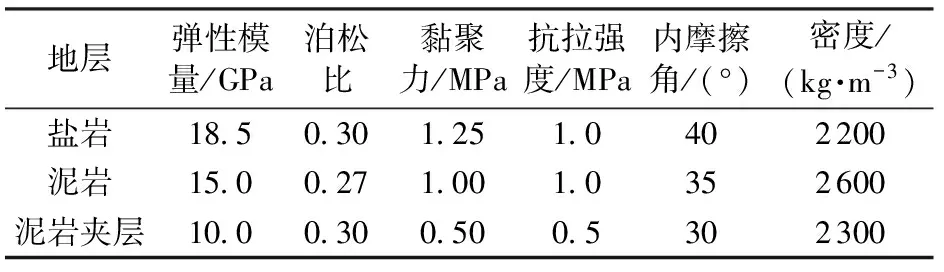
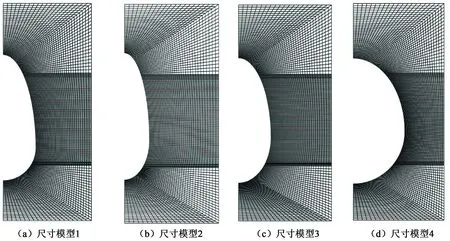
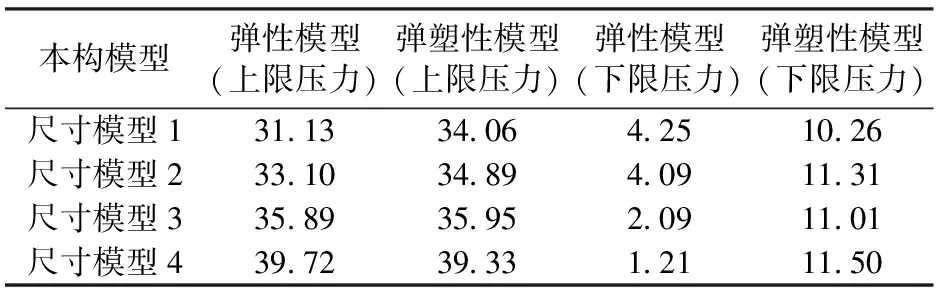
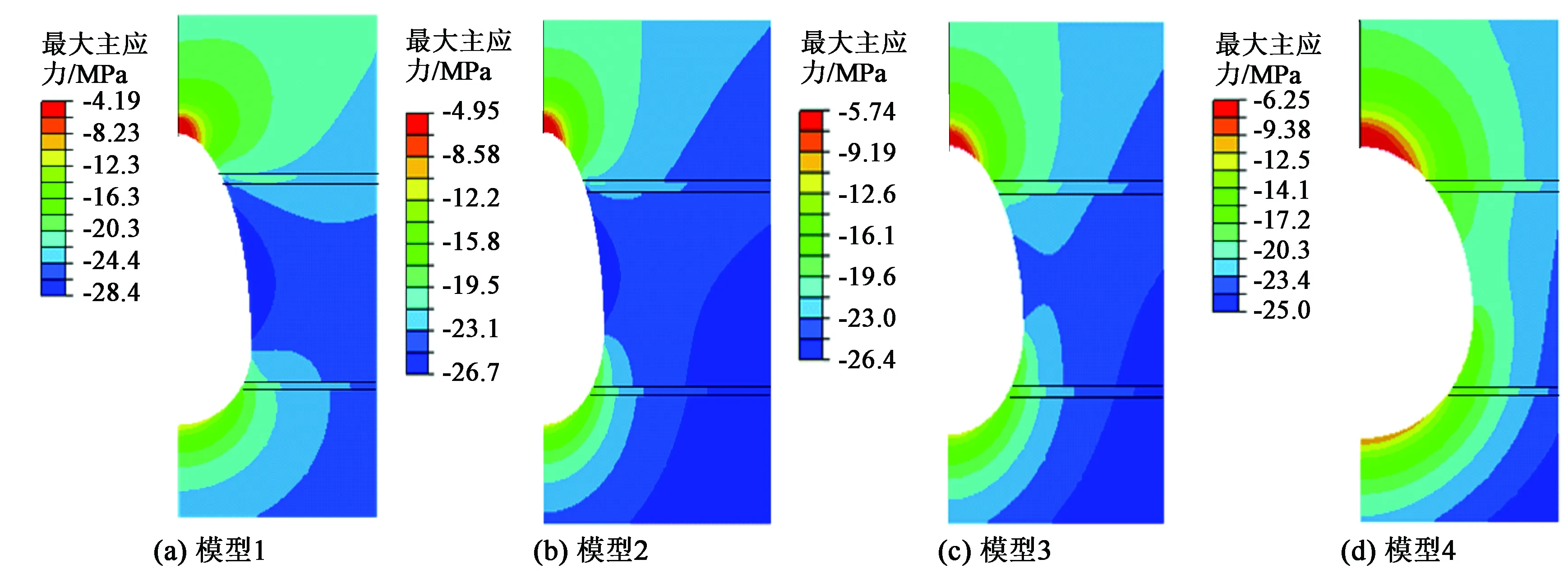
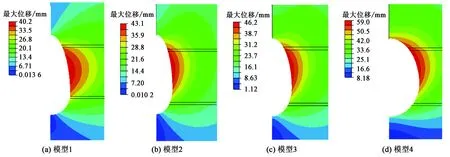
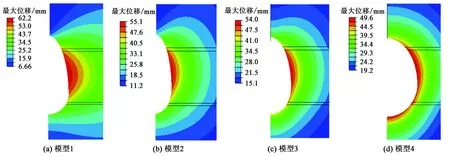
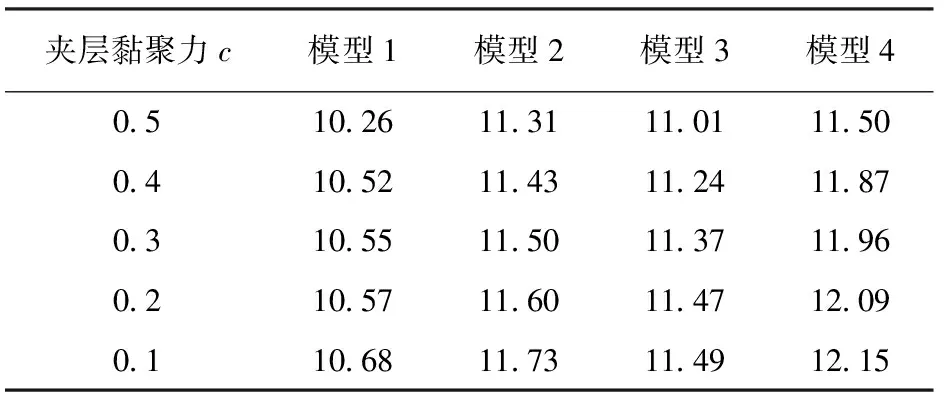
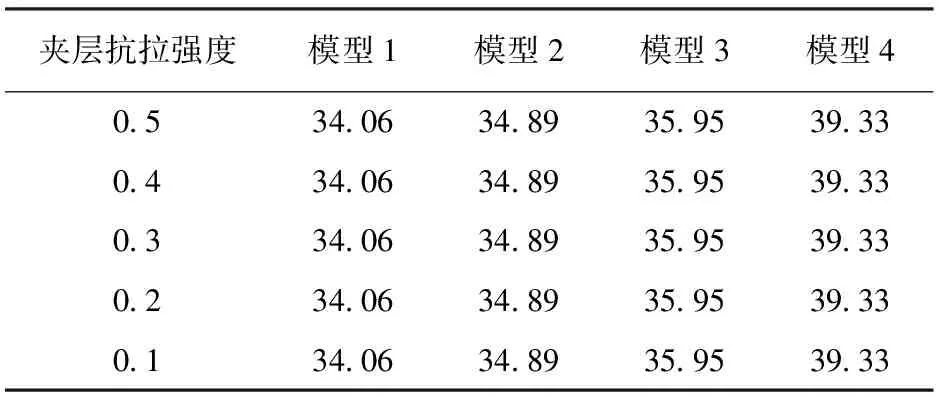
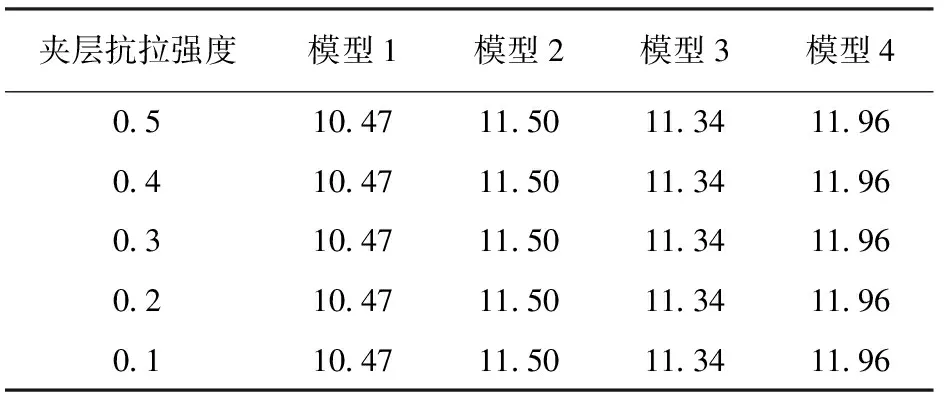
式中,ψ为剪胀角,rad;c0为初始黏聚力,MPa;e为π平面上的偏心率,0.5 图2 修正Mohr-Coulomb屈服准则Fig.2 Modified Mohr-Coulomb yield criterion 为了保证储气库安全,储气库上限压力应满足:①最大拉应力准则[10];②水力压裂准则。水力压裂裂缝总是沿着阻力最小的路径扩展[11],即垂直于最小主应力平面产生和扩展。储气库内压增加时,可能导致周边盐岩产生微裂缝甚至为张开型裂缝;根据弹性平面理论,储气库上限压力应满足 pmax<σmin=0.001λγh. (5) 式中,pmax为储气库上限压力,MPa;σmin为最小地应力,MPa;λ为侧压系数;γ为地层的平均重度,kN·m-3;h为地层平均厚度,m。 当储气库内压过低时,将导致围岩变形过大,影响其稳定性,故储气库下限压力应满足:①顶板稳定原则。当储气库腔体内压低于所处围压地应力时,腔体顶板向腔内下沉,为防止顶板的过度变形及其底部出现张性开裂,储气库下限压力必须满足相应的变形约束要求;当下限压力过高时,垫气量加大,使得可采气量少,储气库运营经济性较差;②蠕变控制原则。地下盐岩储气库在注、采循环过程中,盐岩经历加压—压力释放—再加压过程,盐岩将在原始应力与储气库内压差的作用下产生蠕变,导致储气库腔体体积过度收敛,减小库容。 为防止围岩产生过度变形,影响储气库使用寿命,综合国内外各种研究成果[12],建议储气库下限压力应满足 pmin≥4.0 . (6) 式中,pmin为储气库下限压力,MPa。 以中国某拟建层状盐岩地下储气库为工程背景。根据现场地质条件该拟建储气库位于地下约1 000 m深岩层,地质剖面结构示意图如图3所示。该拟建储气库计算区域的顶层埋深为700 m,各岩层基本水平分布,厚度略有差异。为便于简化计算,各岩层厚度取平均值,其中上覆泥岩层和下卧泥岩层厚度均为300 m;建腔盐岩层厚度从上至下分别为53、64和42 m;上部和下部泥岩夹层厚度分别为3.5和3 m。 图3 地质剖面结构示意图Fig.3 Geological section structure diagram 不同于国外海相沉积形成的盐丘,中国湖相沉积形成的含夹层互层盐岩不适宜修建长柱形储气库。考虑到腔体的稳定性及现有的造腔工艺,腔体形状一般设计为椭球腔、球形腔或梨形腔。本工程实际的储气库腔体形状设计采用梨形腔,即上部为椭球形,下部为球形,保持腔体长轴不变,通过变化短轴尺寸寻找最优化储气库形状尺寸。 基于该工程的实际地质条件,建立分析模型,其中模型水平方向长度为400 m,深度方向长度共计为765.5 m,包括165.5 m厚盐岩层及夹层,盐岩层上下各取300 m厚的泥岩层。计算模型的左右边界分别受到水平方向的位移约束,下部边界受到垂向方向的位移约束,上表面为自由边界,未受任何约束。储气库由上部半椭球体和下部半球形体组成,半椭球长半轴与短半轴之和保持96 m不变,通过变化长轴与短轴,形成如图4所示的4种储气库腔体尺寸结构模型示意图,其中储气库腔体的长短轴之比逐渐减小,分别为71/25、66/30、61/35和56/40。 图4 储气库腔体形状尺寸模型示意图Fig.4 Gas storage chamber structure size diagram 上覆岩层的重力简化为计算模型的上表面荷载,根据地层的实际厚度及地层平均密度计算等效荷载为16.8 MPa,竖向应力为自重应力,水平应力为自重应力与侧压系数乘积。根据盐岩、泥岩及泥岩夹层单轴、三轴实验结果,其计算力学参数如表1所示[12];假定盐岩层界面之间的颗粒间连接紧密、相互嵌入咬合、孔隙极小、界面处无损伤,且腔体周边不存在微裂缝[13-14],有限元计算模型如图5所示。 表1 地层计算力学参数 图5 有限元计算模型Fig.5 Finite element calculation model 3.4.1长短轴变化对储气库极限压力影响 根据修正的Mohr-Coulomb破坏准则对4种模型分别进行储气库上限压力和下限压力计算,结果如表2所示。从表2可知,弹性模型计算得到的上限压力随储气库长短轴之比减小而增大,弹塑性模型得到的上限压力变化规律与弹性模型结果相似;弹性模型计算得到的下限压力随储气库长短轴之比减少而减小,而弹塑性模型计算得到的下限压力基本不随储气库长短轴之比而变化。 表2 不同模型下储气库极限压力Table 2 Limit pressure of gas storage under different models MPa 图6~8分别为4种储气库尺寸模型上限压力状态下的等效塑性应变、最大主应力及最大位移幅值云图。由图可知:随着储气库腔体长短轴之比减少。储气库最大塑性应变减小,其中,最大应变为1.38×10-2,最小应变为5.83×10-3,应变区域逐渐扩大且夹层出现微小应变区域;储气库围岩均处于压应力状态,最大主应力逐渐增大,夹层处最大主应力存在突变,且突变值逐渐减小;储气库围岩平均最大位移值呈递增形式,最大位移为59.0 mm,围岩最大位移处发生在腔体中上部,且随着腔体长短轴之比的减小逐渐上移,但夹层处位移不存在明显的突变。 图6 储气库上限压力状态下的等效塑性应变Fig.6 Equivalent plastic strain at elastic-plastic the maximum pressure of gas storage 图7 储气库上限压力状态下的最大主应力Fig.7 The maximum main stress at elastic-plastic the maximum pressure of gas storage 图8 储气库上限压力状态下的最大位移Fig.8 The maximum displacement at elastic-plastic the maximum pressure of gas storage 图9~11分别为4种储气库模型的下限压力作用下的等效塑性应变、最大主应力及最大位移幅值云图。由图可知:随着储气库腔体长短轴之比的减少储气库最大塑性应变减小,其中最大应变为1.27×10-1,最小应变为5.37×10-2,其应变相对于上限压力时增加较多,储气库顶端塑性区消失,夹层塑性区基本不变;储气库围岩均处于受压状态,最大主应力逐渐增大,夹层与盐岩层交界面处最大主应力存在突变,且该值变大;储气库围岩平均最大位移值呈递减形式,最大位移为62.2 mm,围岩最大位移处发生在腔体中部,且随着腔体长短轴之比的最大位移范围扩大,夹层处位移突变逐渐明显。 图9 储气库下限压力状态下的等效塑性应变Fig.9 Equivalent plastic strain at elastic-plastic the minimum pressure of gas storage 图10 储气库下限压力状态下的最大主应力Fig.10 The maximum main stress at elastic-plastic the minimum pressure of gas storage 图11 储气库下限压力状态下的最大位移Fig.11 The maximum displacement at elastic-plastic the minimum pressure of gas storage 3.4.2不同夹层黏聚力对储气库极限压力影响 不同黏聚力下含夹层盐岩储气库上限和下限压力分别如表3、 4所示。由表3可知,同一种储气库尺寸模型下,变化夹层黏聚力,储气库上限压力保持不变;随着储气库腔体长短轴之比减少,储气库上限压力为非均匀增大,上限压力为39.33 MPa。由表4可知,夹层黏聚力逐渐减小,同一类型储气库下限压力逐渐增大;夹层黏聚力相同时,随着储气库腔体长短轴之比减少,储气库下限压力增大,增大无明显规律,下限压力为10.26 MPa。 表3 不同黏聚力下含夹层盐岩储气库上限压力Table 3 Laminated salt rock gas storage the maximum pressure under different cohesions MPa 表4 不同黏聚力下含夹层盐岩储气库下限压力Table 4 Laminated salt rock gas storage the minimum pressure under different cohesions MPa 3.4.3不同夹层抗拉强度对储气库极限压力影响 不同抗拉强度下含夹层盐岩储气库最大和下限压力分别如表5、 6所示。夹层黏聚力不变,抗拉强度变化,同种类型储气库极限压力的变化规律与表3、4相似。对比表3、5和4、6知,当夹层与盐层界面处未受扰动时,储气库密封性能良好,储气库极限压力受夹层影响不明显。 表5 不同抗拉强度下含夹层盐岩储气库上限压力Table 5 Laminated salt rock gas storage the maximum pressure under different tension strength MPa 表6 不同抗拉强度下含夹层盐岩储气库下限压力Table 6 Laminated salt rock gas storage the minimum pressure under different tension strength MPa (1)随着储气库腔体长短轴之比减小储气库极限压力均增大,上限压力增大幅度明显高于下限压力增大幅度,储气库上限压力受腔体尺寸影响较下限压力明显。 (2)同种类型储气库上限压力不随夹层黏聚力和抗拉强度变化而变化,下限压力受夹层黏聚力和抗拉强度力学特性影响较小,夹层的存在对该储气库极限压力的影响可忽略不计。 (3)随着储气库腔体长短轴之比减少,上限压力下储气库顶部塑性区和变形逐步向围岩扩散,且主要集中在储气库上部,下限压力数值解下储气库夹层塑性区大小基本不变,围岩变形呈环形均匀分布。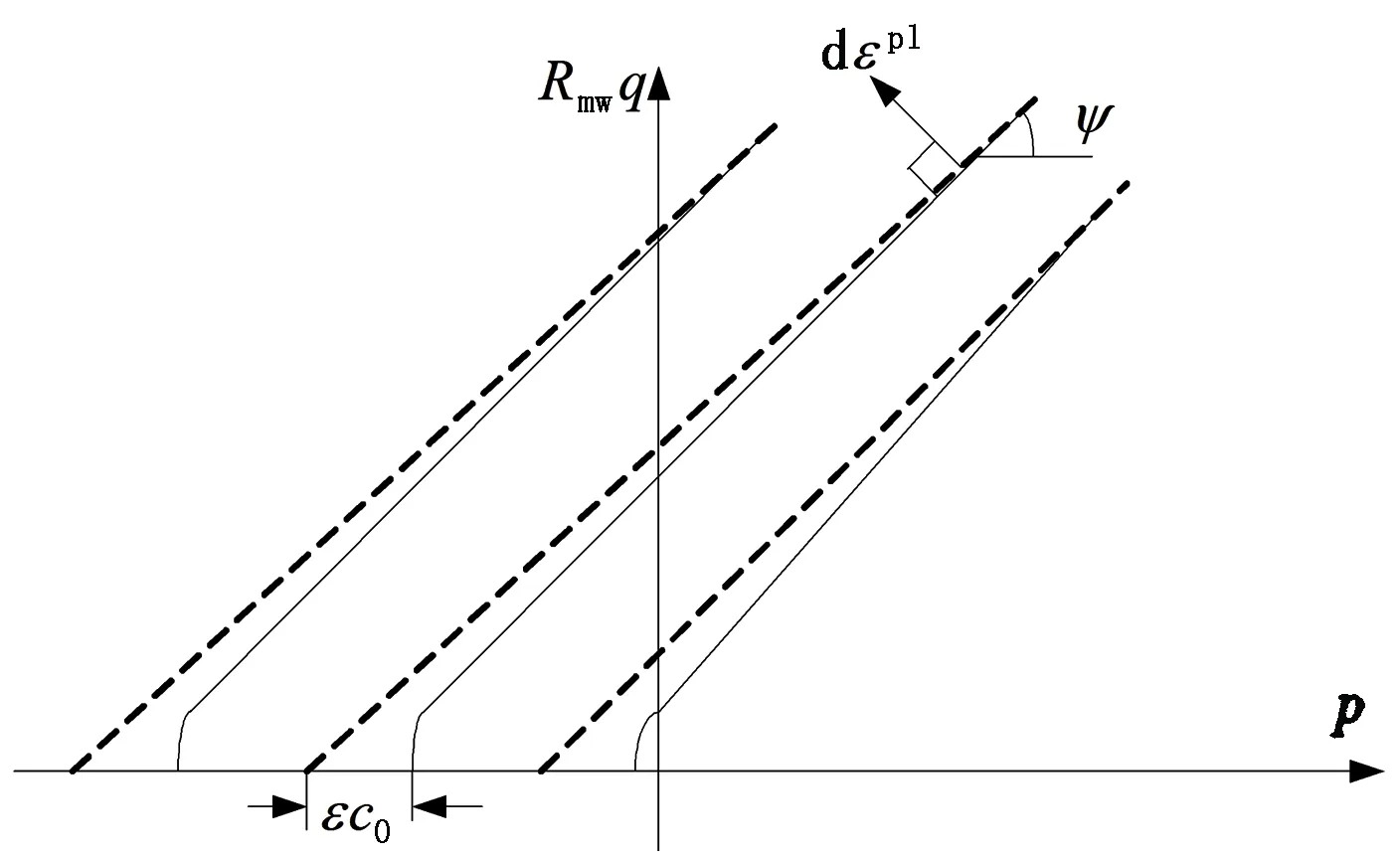
2 盐岩储气库极限压力判定准则
2.1 上限压力
2.2 下限压力
3 算例分析
3.1 工程概况
3.2 储气库洞室方案选取原则
3.3 模型尺寸和边界条件

3.4 计算结果分析




4 结 论
