考虑表面扩散的实际状态页岩气表观渗透率新模型

李冬冬, 张艳玉, 孙晓飞, 赵风凯, 崔晓朵, 乔伟泽, 苏玉亮

(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中国石化胜利油田分公司勘探开发研究院,山东东营 257015;3.辽河油田安全环保技术监督中心,辽宁盘锦 124010)

页岩气储层以发育多种类型的纳米级孔隙为特征[1],孔隙度一般小于6%,渗透率一般小于0.001×10-3μm2[2]。页岩气在纳米孔隙中的流动形态为滑脱流或过渡流[3],目前描述上述过程的主要方法有格子Boltzmann方法[4-5]、蒙特卡洛方法[6-7]以及渗流力学方法等。其中,渗流力学方法研究尺度广(从孔隙尺度到油藏尺度),计算量小,广泛应于页岩气研究领域。目前,基于渗流力学方法形成的页岩气表观渗透率模型主要有Beskok-Karniadakis[8]、Javadpour[9-10]以及Klinkenberg模型[11],而Jones-Owens[12]、Florence[13]、Ertekin[14]、Michel[15]、Sakhaee-Bryant[16]、Civan[17]等模型以Klinkenberg模型为基础,主要区别在于滑脱系数bk的计算方法不同。上述3类模型均假设页岩气为理想气体,未考虑页岩气分子的大小及分子间的相互作用力。另外,吸附气和自由气共存的介质中,气体运移机制主要包含自由气的黏滞流和Knudsen扩散以及吸附气的表面扩散。Knudsen扩散描述气体分子与孔隙壁碰撞而引起的气体运移现象,而滑脱效应产生的根源也是气体分子与孔隙壁的碰撞,因此两者从本质上是同一种机制。已有模型仅考虑了自由气的黏滞流以及Knudsen扩散,并未考虑吸附气的表面扩散现象。为了表征实际状态下的页岩气在纳米孔隙中的运移机制,笔者考虑黏滞流、Knudsen扩散以及表面扩散机制,推导实际状态下页岩气的表观渗透率模型。

1　实际状态下页岩气的Knudsen扩散

考虑分子的大小以及分子间的相互作用,假设孔隙为圆形,内壁光滑,气体前进方向为正,则实际状态气体的Knudsen扩散方程[9]为

(1)

其中

式中,JK为页岩气Knudsen扩散质量流量,kg/(m2·s);M为页岩气的相对分子质量,kg/mol;C为页岩气的摩尔密度,mol/m3;DK为页岩气的Knudsen扩散系数,m2/s;r为孔隙半径,m;Z为页岩气的压缩因子;R为通用气体常数,8.314 J/(mol·K);T为温度,K;z为空间变量。

根据实际气体的状态方程pV=nZRT可得,气体的摩尔密度为

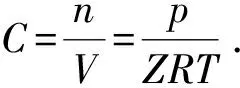
(2)

式中,p为压力,Pa;n为气体的物质的量,mol;V为气体的体积,m3。

将式(2)代入式(1)中可得

(3)

而压缩因子又是温度以及压力的函数,在恒温条件下,有

(4)

对于实际气体,其等温压缩系数[18]为

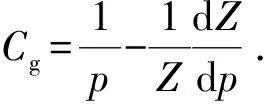
(5)

将式(4)、(5)代入式(3)中,推导可得实际状态下的Knudsen扩散方程为

(6)

式中,Cg为页岩气的等温压缩系数,Pa-1。

2　实际状态下页岩气的黏滞流

根据Hagen-Poiseuille方程[13],页岩气在纳米孔隙中流动时黏滞流质量流量为

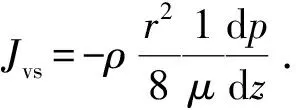
(7)

式中,Jvs为页岩气的质量流量,kg/(m2·s);ρ为页岩气的密度,kg/m3;μ为页岩气的黏度,Pa·s。

根据实际气体的状态方程可得气体的密度为

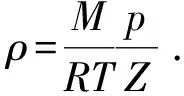
(8)

将式(8)代入式(7)中,推导可得实际状态下页岩气的黏滞流方程为

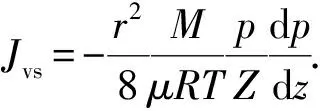
(9)

3　页岩气的表面扩散

由于页岩中存在有机质以及黏土矿物,且页岩的孔隙尺寸为纳米级或微米级,页岩气在孔隙中存在吸附现象。孔隙内壁的吸附气会沿着吸附层移动,这种现象称为表面扩散现象。页岩气的表面扩散流量由Fick扩散定律计算[19-20]为

(10)

式中,JS为页岩气表面扩散的质量流量,kg/(m2·s);DS为页岩气的表面扩散系数,m2/s;CS为页岩气的吸附量,mol/m3。

式(10)中页岩气的吸附量CS的计算方法与页岩气的吸附类型有关。大量文献表明,甲烷在页岩中的吸附为单层吸附,满足Langmuir等温吸附定律[21-23],因此有

(11)

将式(11)代入到式(10)中,推导可得页岩气的表面扩散方程为

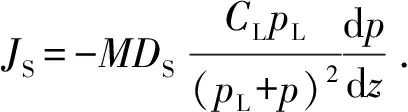
(12)

式中,CL为Langmuir最大吸附量,mol/m3;pL为Langmuir压力,表示吸附量为最大吸附量的一半时所对应的压力,Pa。

表面扩散系数DS=DS0f(θ),DS0为表面覆盖率为0时的表面扩散系数,θ为表面覆盖率。Langmuir等温吸附的表面覆盖率定义为

(13)

目前常见的表面扩散系数的计算方法主要分为两类:一类是拟合模型(Hwang-Kammermeyer模型[20]、Suzuki-Fujii模型[24]等),需要通过试验数据拟合确定模型中的参数;另一类是理论模型(HIO模型[25]、改进的HIO模型[26]、Kapoor-Yang模型[27]、Chen-Yang模型[28]以及Do模型[29]等),主要根据孔隙和气体的物性参数计算表面扩散系数。由于第二类模型比第一类模型适用性更强,本文中采用第二类模型中的5种方法计算甲烷的表面扩散系数,计算结果如图1所示。由此可知,当表面覆盖率接近1时,HIO模型、Do模型以及Kapoor-Yang模型计算的表面扩散系数趋向于无穷大,因此这3种模型适用性差。改进的HIO模型虽不存在此问题,但此模型假设存在第2吸附层,与页岩气藏单层吸附不相符。Chen-Yang模型不但考虑了孔隙表面的非均质性,并且覆盖率为1时表面扩散系数为有限值。因此采用Chen-Yang模型,公式为

(14)

其中

式中,β为阻塞常数,当β=0时此模型简化为HIO模型;kb为阻塞速率常数,m/s;km为前进速率常数,m/s。

其中,式(14)中DS0的计算方法[30]为

(15)

式中,ΔH为等量吸附热,J/mol。

图1　不同方法计算的甲烷表面扩散系数Fig.1　Methane surface diffusion coefficient calculated by different methods

4　实际状态页岩气的表观渗透率模型

页岩气在纳米孔隙中的流动,在不考虑表面扩散时,总流量为黏滞流流量与Knudsen扩散流量之和[10,31-32];考虑表面扩散时,总流量为自由气的流量与吸附气表面扩散流量之和[20,32]。因此页岩气在纳米孔隙中的总质量流量为黏滞流流量、Knudsen扩散流量以及表面扩散流量之和:

J=Jvs+JK+JS=

(16)

页岩气的体积流量为

(17)

将式(8)、(16)代入式(17),得

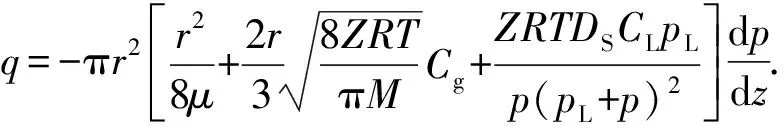
(18)

根据Darcy定律,可推导出实际状态下单一纳米孔隙中页岩气的表观渗透率模型为

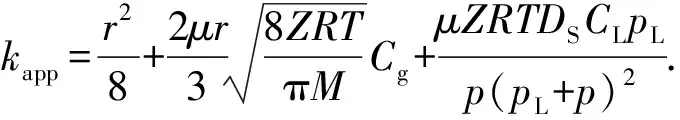
(19)

式中,kapp为页岩气的表观渗透率,m2。

若分别用kvs、kKn和kS表示黏滞流、Knudsen扩散以及表面扩散引起的渗透率,则

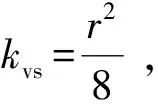
(20)

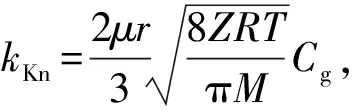
(21)

(22)

若分别用γvs、γKn和γS表示黏滞流、Knudsen扩散以及表面扩散引起的渗透率在总表观渗透率中所占的比重,则

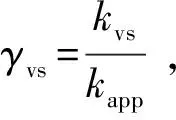
(23)

(24)

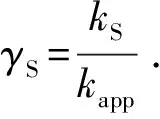
(25)

5　页岩气压缩因子及黏度的计算方法

通过式(19)计算实际状态下页岩气的表观渗透率,需要精确计算页岩气黏度μ以及压缩因子Z。分别以108和116个压缩因子和黏度数据点为依据,系统对比评价5种压缩因子和11种黏度计算方法,提高实际状态下页岩气表观渗透率模型计算的准确性。

将计算所得相对误差、平均相对误差和平均运算时间作为模型评价的依据。

相对误差ERi的计算方法为

(26)

平均相对误差EARi为

(27)

式中,Zi为计算的第i个压缩因子或黏度数据;ZCi为第i个数据点的压缩因子SK图版值或黏度Carr图版值;N为压缩因子或黏度数据点个数。

5.1　压缩因子计算方法

采用HY[18]、DPR[33]、DK[34]、HSM[35]和HMR[36]方法计算108个不同压力和温度下的甲烷压缩因子,并与压缩因子SK图版比较,如图2所示。

由图2可知,DK方法误差最小,为0.53%;而HY方法的运算时间最大,DPR、DK方法次之,HSM、HMR方法最小。综合误差及运算时间两方面因素,应采用DK方法计算页岩气的压缩因子。

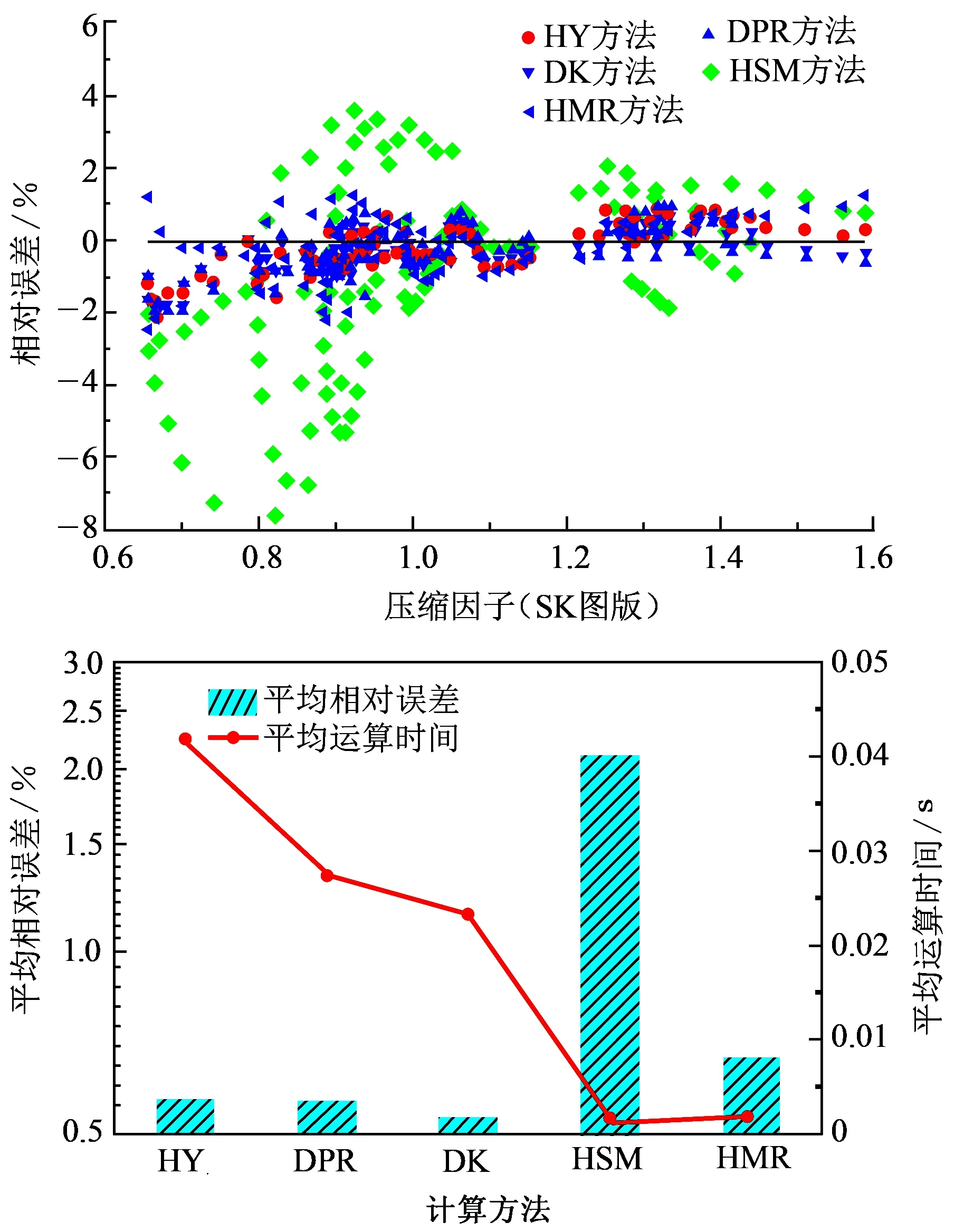
图2　甲烷压缩因子相对误差和平均相对误差及运算时间Fig.2　Relative error and average relative error of methane Z-factor by different methods

5.2　黏度计算方法

分别采用API剩余黏度[18,33]、DPS[37]、SLP[37-38]、HMR[36]、JH[39]、HMS[40]、LGE[38]、Els[41-42]、LAB[41]、Sutton[41-42]和HJ[41-42]方法计算了116个不同压力和温度下甲烷黏度,并与Carr图版[43]和文献中的数据比较[44],如图3所示。由图3可知,在大气压条件下以及高温高压条件下累积相对误差均为Sutton方法最小,分别为0.6%和2.7%。因此采用基于密度的Sutton方法计算页岩气的黏度。

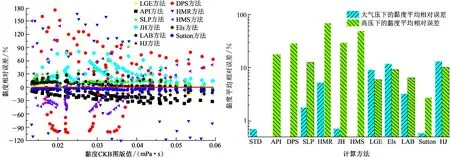
图3　不同模型计算的黏度相对误差和平均相对误差直方图Fig.3　Relative error and average relative error of methane viscosity by different methods

6　模型验证

Roy等[45]通过试验测量了Ar气通过由长直圆柱纳米孔隙组长的均质多孔介质的质量流量,试验所采用的材料纳米孔隙长度L为60×10-6m,纳米孔隙半径r为106×10-9m,出口压力pout为4.8 kPa,压差Δp为87.4～916.9 kPa,温度T为300 K,气体的黏度μ为0.222 mPa·s,相对分子质量M为39.948 g/mol,出口Knudsen数为7.36。将本文中所建模型与现有模型计算结果比较[12-17],如图4所示。

图4　试验数据与模型计算结果对比Fig.4　Comparison of model computation results and experimental data

由图4可知,本文中模型计算结果与Roy试验测量结果拟合程度高,拟合效果好,误差为3.02%,而其余模型计算的质量流量均小于试验值,并且有较大差距,原因在于Jones-Owens、Florence、Ertekin等模型并不能很好地描述页岩气在纳米尺度孔隙中的运移。本文中所建模型可以准确地描述稳态条件下实际状态页岩气在纳米孔隙中的渗流过程。

7　页岩气表观渗透率影响因素

7.1　表面扩散的贡献

计算不同孔隙半径、不同压力条件下的表面扩散渗透率比重γS,如图5所示。表面扩散渗透率比重表征了表面扩散机制对页岩气表观渗透率的贡献。由图5可知,表面扩散渗透率比重随压力的增大而减小,也随孔隙半径的增大而减小。另外,孔隙半径为1 nm、压力分别为0.1和20 MPa时,表面扩散引起的渗透率变化在总渗透率中所占比例可达75%、30%,说明在页岩纳米孔隙中,不管在低压条件下还是油藏条件下,均不能忽略表面扩散对渗透率的影响。

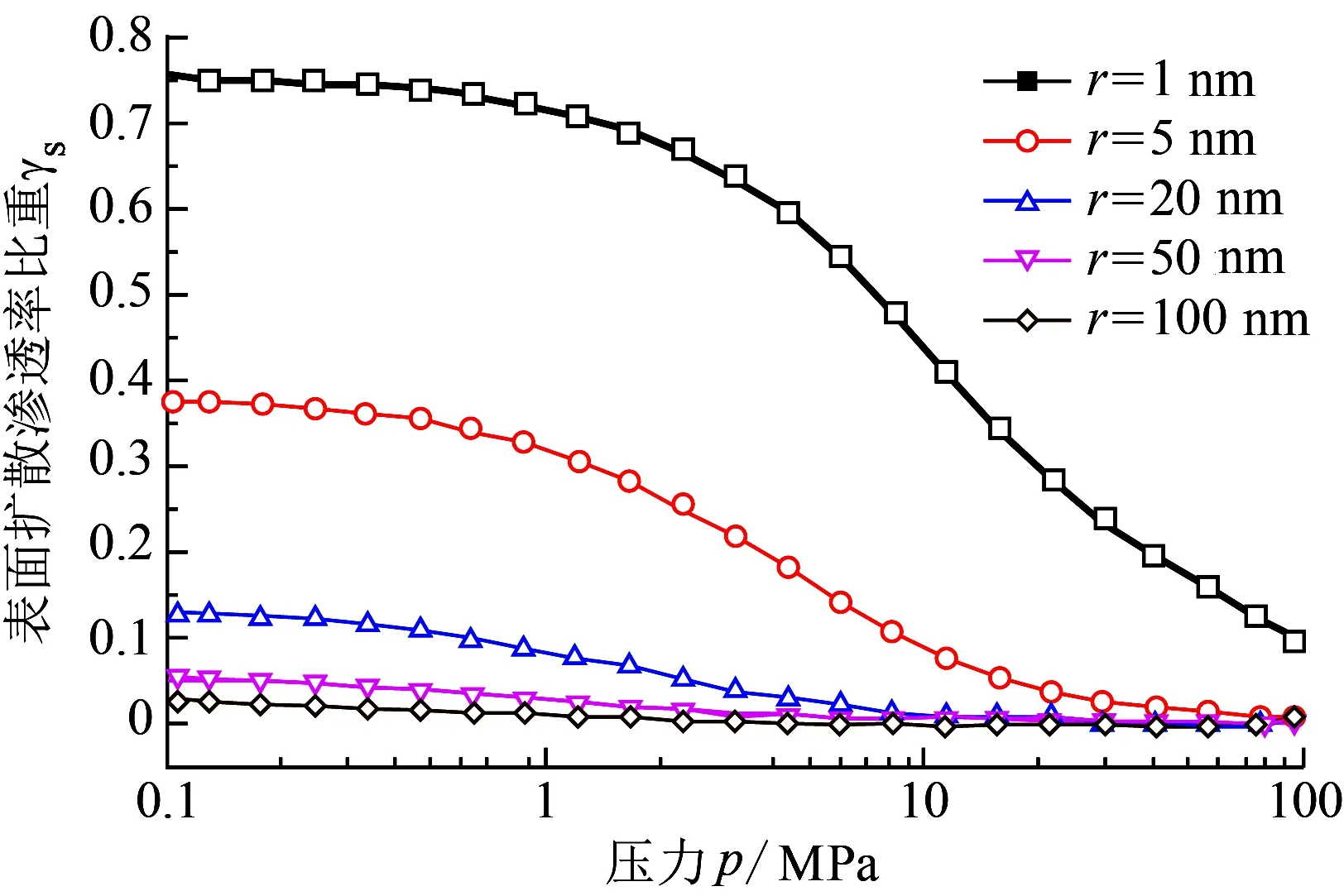
图5　不同压力及孔隙半径下表面扩散渗透率比重Fig.5　Effects of pressure and pore radius on surface diffusion permeability fraction

7.2　孔隙半径与压力的影响

计算不同孔隙半径下表观渗透率、黏滞流渗透率比重、Knudsen扩散渗透率比重以及表面扩散渗透率比重,如图6所示。由图6可知:①表观渗透率随孔隙半径增加而增加,随压力的增加而减小;②黏滞流渗透率比重随孔隙半径及压力的增加而增加;③低压条件下,Knudsen扩散渗透率比重随孔隙半径增加,呈现先增加后减小的趋势,且压力越大,曲线峰值越靠左;高压条件下,Knudsen扩散渗透率比重随孔隙半径的增加而减小,如图6(c)所示;④表面扩散渗透率比重随孔隙半径的增加而急剧减小,如图6(d)所示,且压力越低,孔隙半径的影响越明显。

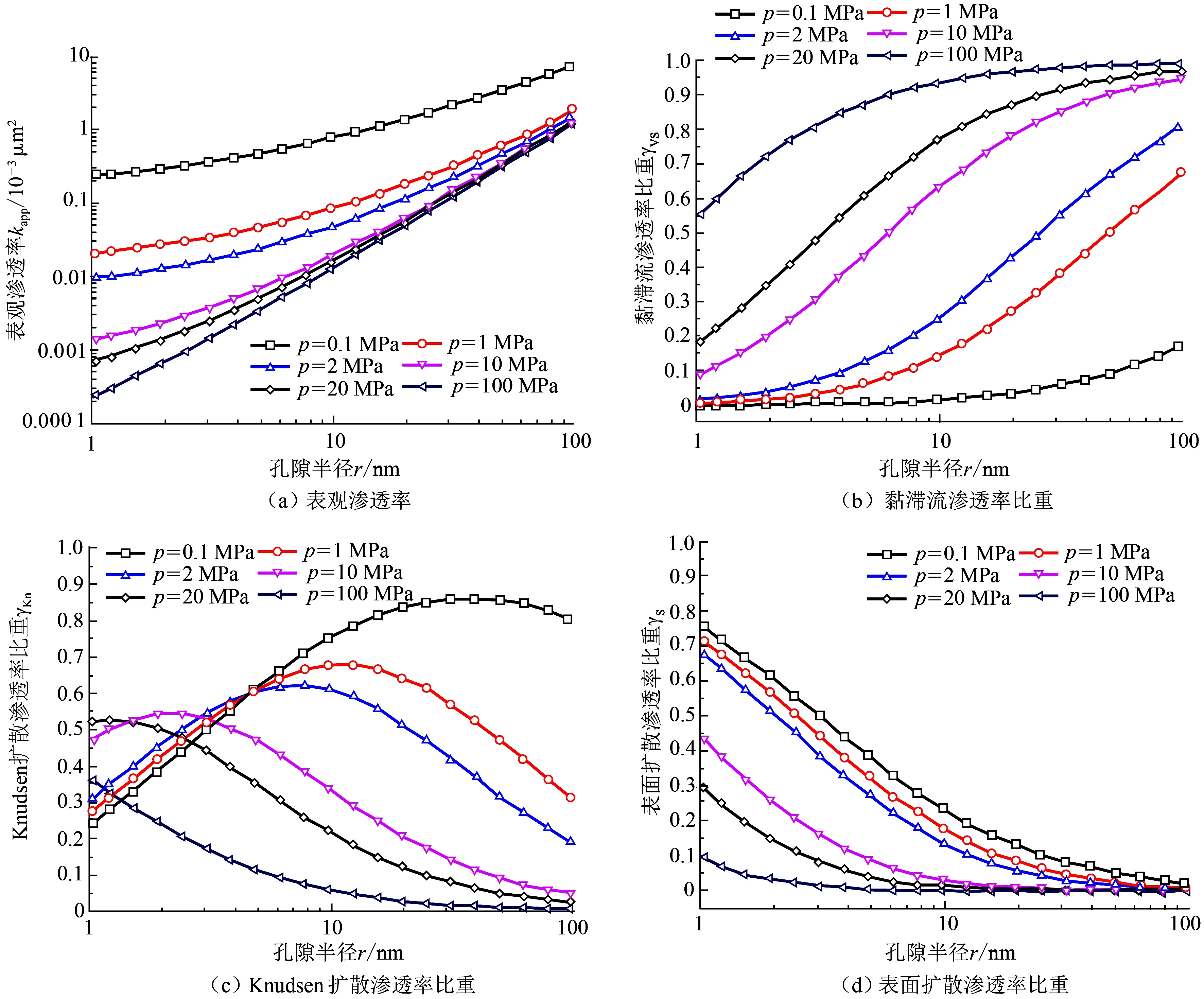
图6　不同压力下孔隙半径对表观渗透率及各比重的影响Fig.6　Effects of pore radius on apparent permeability and fractions at different pressures

7.3　温度与压力的影响

不同压力下温度对表观渗透率及各比重的影响如图7所示。由图7可知:①表观渗透率随温度的增大而增大,且压力越小,图7(a)中曲线的斜率越大,温度对表观渗透率的影响越大;②图7(b)中,黏滞流渗透率比重随温度的升高而降低,且压力太高或太低时,温度的影响不大,反而压力处于中间状态,曲线的变化较明显,温度的影响较大;③图7(c)中,Knudsen扩散渗透率比重低压下随温度的升高而降低,高压下随温度的升高而升高;④图7(d)中,表面扩散渗透率比重随温度的升高而升高,且低压下曲线的斜率越大,温度的影响越大。

7.4　表面扩散参数与压力的影响

Langmuir最大吸附量、Langmuir压力及等量吸附热对页岩气的表观渗透率、黏滞流渗透率比重及Knudsen扩散渗透率比重影响不大,但对表面扩散渗透率比重有较大影响,如图8所示。由图8可知:表面扩散渗透率比重随Langmuir最大吸附量增大而增大,且低压下,曲线斜率更大,Langmuir最大吸附量的影响更明显;低压下,表面扩散渗透率比重随Langmuir压力的增加而减小,且压力越大,曲线斜率越小,说明Langmuir压力对表面扩散渗透率比重的影响越小,高压下Langmuir压力对表面扩散渗透率比重影响甚微;表面扩散渗透率比重随等量吸附热的增加而减小,且压力越低,曲线变化越明显,等量吸附热的影响越大。

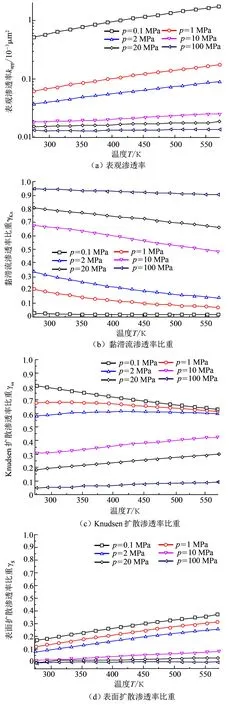
图7　不同压力下温度对表观渗透率及各比重的影响Fig.7　Effects of temperature on apparent permeability and fractions at different pressures

图8　Langmuir最大吸附量、Langmuir压力及等量吸附热对表面扩散渗透率比重的影响Fig.8　Effects of the max Langmuir adsorption concentration,Langmuir pressure and isosteric adsorption heat on surface diffusion permeability fraction

8　结　论

(1)页岩气在纳米孔隙中运移,包含自由气的黏滞流、Knudsen扩散以及吸附气的表面扩散机制。

(2)在页岩纳米孔隙中,在低压及油藏条件下均不能忽略表面扩散对渗透率的影响。

(3)压力和孔隙半径对表观渗透率的影响最大;Langmuir最大吸附量、Langmuir压力、等量吸附热主要影响表面扩散渗透率比重。在低压和高压条件下,温度和孔隙半径对模型的影响呈现不同的规律,低压下各参数的影响更加明显。

(4)压力越低,孔隙半径越小,表面扩散对总表观渗透率的贡献越大。