民用飞机反尾旋研究与尾旋风洞试验

颜　巍　黄灵恩　陈　功 /

(上海飞机设计研究院，上海201210)

0　前言

尾旋是飞机的极限飞行状态之一，若飞机不幸陷入此一状态，飞行员要毫不犹豫地通过正确的舵面组合操纵来迫使飞机迅速地从尾旋中改出。传统的尾旋改出方式有[1]：“三中立”法、“反舵推杆”法、“平中顺”法、“舵回中推杆”法和“反舵杆回中”法等。其中“三中立”法操作最为简便，飞行员无需判别尾旋的方向；“反舵推杆”法操作改出效果最佳，但需要准确判断尾旋的方向，改出后杆舵要及时回中；“平中顺”法操作适用于方向舵近乎完全失效的状态。在飞机A的研究过程中，从人机的终极安全角度考虑，需要研究飞机是否具有尾旋改出的能力，以备在极端危险情况下，飞行员具备最佳的处置方式。由于静态测力结果为飞机总的空气动力的主量，所以首先在常规风洞中进行了飞机缩比模型的大攻角静态测力试验。飞机尾旋运动以偏航运动最为显著，所以首先对方向舵、副翼的单独偏转的影响进行分析；此外为了降低攻角，要对升降舵的单独偏转的影响进行分析。在大攻角条件下，飞机舵面效率会大幅下降，有时甚至完全丧失。在舵面操纵无效的情况下，反尾旋伞就是人机存活唯一的、最后的选择，所以设计一款合适的反尾旋伞是极端重要的，它关系到飞行员的生命安全和价值上亿元飞机的保全。

1　舵面组合偏转法改出尾旋

1.1 方向舵的影响

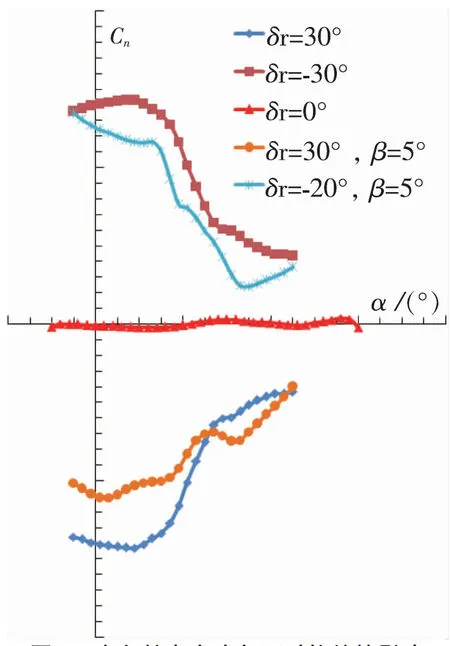
图1　方向舵在大攻角下对偏航的影响

为了将处于尾旋状态的飞机改出，首先要制止飞机的旋转，即降低偏航角速率，为此需要将方向舵回中或逆尾旋方向偏转方向舵，消除那些有利于、可能助长或保持飞机旋转的顺尾旋偏航力矩。图1中展示了取自飞机模型大攻角试验结果，β=0°时的不同方向舵偏度下的Cn随攻角变化关系。当r=-30°时，近似对应飞机右尾旋，Cn为正值。若方向舵回中，即r=0°，Cn值降到零附近，即消除了顺尾旋的偏航力矩，飞机将会逐渐停止旋转。若方向舵向反方向满偏，即r=30°，则Cn值全部反号，产生了逆尾旋偏航力矩，迫使飞机停止旋转的时间将更短。从小攻角到大攻角，方向舵效率下降了约70%。图1还展示了β≠0°时的不同方向舵偏度下的Cn随攻角变化关系。当r=30°时，近似对应飞机左尾旋，外侧滑，Cn为负值。若方向舵向反方向偏转，即r=-20°，则Cn值全部反号。大攻角条件下，方向舵效率仅有约30%。这个结论说明，该飞机在尾旋中即使带有外侧滑，只要逆尾旋方向偏转方向舵就能制止旋转，当然，从实施改出工作到停止旋转的时间长短与飞机尾旋改出前的初始条件有关，如攻角的大小，随着攻角的增大，方向舵的效率会下降，改出时间会延长。可以看出飞机尾旋中若逆尾旋方向偏转方向舵是能够提供抗尾旋的偏航力矩的。

1.2 副翼的影响

飞机除了方向舵能够提供主要的偏航力矩外，副翼偏转在提供滚转的同时也能提供一小部分偏航力矩。操纵副翼的原因是，随着攻角的增大，方向舵受平尾/机身/机翼洗流的影响逐渐加大，当超过某一攻角，方向舵效率会全部丧失，此时唯一能提供偏航力矩的就是偏转副翼，因为副翼处于机翼的外翼，不受其它部件洗流的影响，且气动中心到重心处的力臂较长。图2中展示了β=0°时的不同副翼偏度下的Cn随攻角变化关系。由于在大攻角条件下副翼所提供的偏航力矩出现反号现象，所以若在飞机左尾旋中，向右压操纵杆反而加剧偏航的程度，而向左压操纵杆可以产生逆尾旋的偏航力矩，有助于尾旋改出。图2中展示了β≠0°时的不同副翼偏度下的Cn随攻角变化关系。在有侧滑的大攻角条件下，左、右压杆对Cn的影响的趋势基本相同，但量级不同。飞机左尾旋中，向右压操纵杆会加剧偏航的程度，若向左压操纵杆会减小顺尾旋偏航力矩的量级。可以看出飞机尾旋中若顺尾旋方向偏转副翼能够提供小量级的抗尾旋偏航力矩。

1.3 升降舵的影响

由于没有进行飞机模型的旋转天平试验，只能用飞机模型大攻角静态测力试验结果来近似地评估飞机在尾旋改出中升降舵的作用。图3展示了取自大攻角试验结果，飞机模型基本构型条件下，不同升降舵偏度所对应的俯仰力矩系数曲线关于x轴的镜像曲线(Cm_气)与基于理论计算的不同旋转角速度条件下的惯性上仰力矩曲线(Cm_惯)之间的关系，其中Cm_惯=f(α，ω，Ix，Iy，q，S，c)。图中红色虚线对应了δe=-30°，即顺尾旋方向偏转升降舵，这条线与不同旋转角速度条件下的惯性上仰力矩曲线均有交点，即气动下俯力矩与惯性上仰力矩的平衡点，说明δe=-30°条件下是会出现平衡尾旋的，但从图中不能判定每一个交点的稳定性。图中黑色虚线对应了δe=0°，即升降舵回中，绿色虚线对应了δe=15°，即逆尾旋方向偏转升降舵。根据公开的资料，尾旋试验飞机模型的旋转角速度没有超过330°/s的情况，大攻角条件下，黑色虚线(升降舵中立)和绿色虚线(逆尾旋偏转升降舵)均在ω=330°/s所对应的曲线上方(土黄色实线)，所对应的含义是δe=0°/15°所产生的气动下俯力矩大于惯性上仰力矩，即升降舵中立与逆尾旋偏转升降舵均有能力将飞机从尾旋状态改出。当然在实际操作中，首先需要逆尾旋方向偏转方向舵制止飞机的旋转。

1.4 平尾-升降舵和垂尾-方向舵的综合影响

对于飞机尾旋改出能力的评估，除了包括对平尾-升降舵和方向舵各自独立的评估，还要将两者综合起来考虑和分析。 Ralph W Stone和Sanger Burk[2]等人为了研究飞机的尾段布局对飞机尾旋改出特性的影响，利用一个1/10的飞机模型在NASA兰利研究中心Φ=20 ft的立式风洞进行了旋转天平试验，通过试验来研究平尾-升降舵和垂尾方向舵对尾旋改出的影响。试验结果显示若固定某一尾旋攻角，且当垂尾位置相对重心位置固定时，增加平尾气动中心到飞机重心的距离，将导致飞机的尾旋攻角减小，反之，则使得飞机的尾旋攻角增大。若固定平尾-升降舵和方向舵的位置，即固定各自气动中心到飞机重心的距离，随着尾旋攻角的增大，即由陡尾旋向平尾旋方向发展，垂尾-方向舵受平尾-升降舵洗流区的影响逐渐增大，使得垂尾-方向舵的偏航力矩随之减小，表明使用方向舵偏转迫使飞机停止旋转的能力在下降。美国NASA兰利研究中心立式风洞的研究人员(Neihouse、Lichtenstein、Pepoon，1946年)和英国RAE的研究人员(E. Finn，1946)[3]在进行了长期而大量的试验后，总结出了一套经典的判定飞机改出尾旋能力的方法：TDPF～[(Ix-Iy)/(mb2)]判据法。其中TDPF为“Tail Damping Power Factor”，这个指示参数由TDR(Tail Damping Ratio)和URVC(Unshielded Rudder Volume Coefficient)两部分组成，前者影响稳定平衡尾旋的攻角(陡尾旋还是平尾旋，在早期研究中没有缓尾旋的定义)，后者指示未受平尾-升降舵洗流影响的方向舵有效面积和力臂长度。它们的数学表达式如下：

TDPF=URVC × TDR

(1)

其中：TDR=(SFL2)/[S(b/2)2]，URVC=(SRL1)/(Sb/2)

SF为平尾下方的机身外表面在机身对称面的投影面积；SR为未受平尾和升降舵洗流影响的，仍然能够保持舵面效率的那部分方向舵的面积在机身对称面的投影面积；L为飞机重心到SF几何中心的距离；L1为飞机重心到SR几何中心的距离，如图4所示。

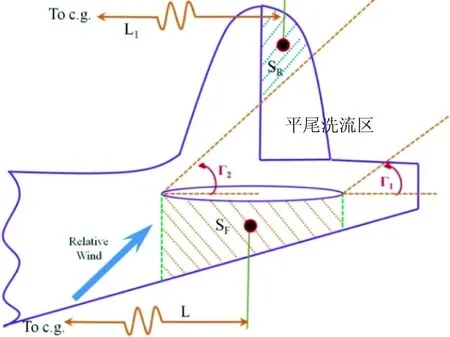
图4　TDPF～[(Ix-Iy)/(mb2)]判据法所定义的相关几何参数

首先求出TDR，若TDR>0.019，平尾当地攻角可以假定为αtail=30°，则Г1=15°，Г2=45°。根据这个定义，从飞机的3D数模上可以近似的求出SR的面积，进而可以求出URVC，最后求得TDPF。

为了完成尾旋改出能力的判定，还需要计算飞机的偏航力矩惯量参数(Inertia Yawing-Moment Parameter)：[(Ix-Iy)/(mb2)]。此外由于飞机的尾旋特性与改出特性和飞机所处的飞行高度(大气密度)有关，所以还需要计算飞机的相对密度系数：μ=m/(ρSb)。在完成以上工作后，就可以将点{TDPF，[(Ix-Iy)/(mb2)]}标注在TDPF～[(Ix-Iy)/(mb2)]判据图中，如图5所示。

图5　TDPF～[(Ix-Iy)/(mb2)]判据图

从图5中可以看出无论前重心所对应的点，还是后重心所对应的点，均处于μ∈(20，35)所对应曲线的上方，且余量很大，这表明在仅使用方向舵条件下，就能够使飞机改出尾旋。

1.5 试验验证

以上分析均是基于静态测力试验结果和经验公式，为了检验以上的结论，需要通过尾旋风洞试验进行相关的验证。为此制作了一个满足外形和动力学相似准则的无动力飞机模型，在尾旋风洞中进行飞机模型的尾旋改出试验。图6展示了在相同模态的尾旋状态下，实施不同改出方法的改出效果比较，比较参数为攻角与偏航角速率。从图中可以清楚的看到采用反舵推杆方法的改出效果最佳，其余两种包含方向舵均回中的改出方法的效果均不及反舵推杆法。这也验证了前文中TDPF～[(Ix-Iy)/(mb2)]判据的准确性，即对于这架常规布局的运输机的尾旋改出，方向舵起到主要的作用。

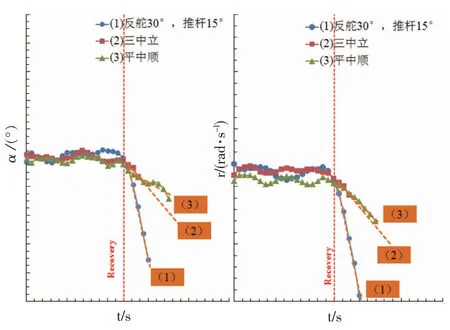
图6　不同改出方法的改出效果比较

2　反尾旋伞改出尾旋

2.1 反尾旋伞的研制

当飞机进入尾旋飞行状态时，试飞员通过舵面操纵无法改出时，则需借助反尾旋伞提供一个附加的低头力矩与偏航力矩，以抵消飞机的惯性上仰力矩与偏航力矩，强行迫使飞机从尾旋中改出，直到恢复正常飞行状态。为了保证反尾旋伞能提供足够的低头力矩和偏航力矩，需要对反尾旋伞的阻力特征值CDSD、连接绳长度Lr、伞载荷进行估算。由于立式风洞试验模型的比例较小，模型内部结构和强度与真实飞机相差较大，同时立式风洞试验主要关注打伞后，伞的阻力对飞机飞行姿态的影响，所以这里不进行伞载荷的估算。为获得合适的反尾旋伞的阻力面积CDSD和连接绳长度Lr，本文使用了工程估算法与原准机类比法两种方法来探讨反尾旋伞的特征尺寸。

2.1.1 工程估算法[4]

确定伞的阻力面积和伞绳长度时，应有一个参考基准，为此可以通过以往的工程经验和已有的经验公式来确定这些参数，以下通过几种不同的工程估算方法进行估算。

1 ) AVP-970提供的工程估算方法

根据AMX飞机尾旋伞研制报告DesignandAirworthinessRequirementsforServiceAircraft，IRVIN阻力伞公司在咨询了英国相关科研机构后，对一架未知尾旋特性的飞机给出的反尾旋伞阻力面积与伞绳长度估算式为：

CDSD=0.091 4×SLs/LA

(2)

Lr≈1.1～1.3L

(3)

式中，CD为反尾旋伞阻力系数，一般取值0.5～0.55；SD为反尾旋伞特征面积(m2)；S为机翼参考面积(m2)；Ls为飞机翼展(m)；LA为伞钩到飞机重心的距离(m)；L为机身长度(m)；Lr为伞绳长度(m)。

2)美国军用标准MIL-STD-1797A提供的工程估算方法

参考MIL-STD-1797A，为了改出严重失速尾旋状态，需要克服惯性上仰力，假定升降舵、方向舵彻底失效，完全依靠反尾旋伞时，反尾旋伞必须提供如下的下俯力矩：

(4)

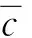
式(4)右边中的第一项为反尾旋伞打开后所克服的抬头静力矩，第二项为反尾旋伞打开后克服飞机的惯性力矩。可以看出飞机俯仰惯性矩越大、飞行时动压越小，那么所需反尾旋伞的阻力面积CDSD越大。MIL-STD-1797A所提供的Lr经验算式如下所示：

Lr=1.1×L

(5)

以上二种估算方法给出的伞的基本参数有一定差异，如表1所示，这是由于这些公式产生于不同的时期以及不同的国家，适用于不同的飞机。这样仅用工程估算法来设计反尾旋伞就带来较大的不确定性，需要引出其它的方法来进行相关的对比才能确定。

表1　经验公式估算的反尾旋伞基本参数

注：A≈B，F≈G 。

2.1.2 原准机类比法[4]

原准机类比法是指通过对已有的民用客机的反尾旋伞数据的统计，按照重量、惯性矩、飞机气动外形等特点进行类比，估算所研制的反尾旋伞的尺寸，图7为典型民用飞机反尾旋伞阻力面积与重量之间的关系。由统计结果可知，飞机A的全机重量与MD-90飞机的全机重量近似，所以可以选用MD-90飞机所使用的反尾旋伞，通过表中可以得到所对应的阻力面积H。通过和上面不同工程估算法所获得的阻力面积的对比，发现原准机类比法获得的阻力面积H与工程估算法中AVP-970和美国MIL-STD-1797A两种方法所估算的阻力面积值较为接近。

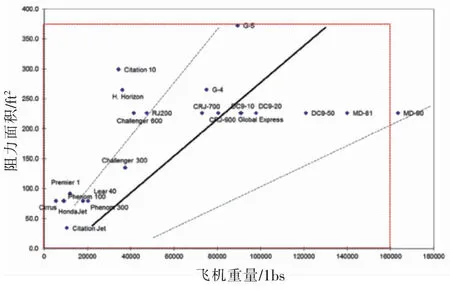
图7　飞机反尾旋伞阻力面积与飞机重量关系

通过图8可以估算出反尾旋伞伞绳长度约W m，与AVP-970和美国MIL-STD-1797A两种工程估算法获得的伞绳长度比较接近。

图8　飞机反尾旋伞伞绳长度与机身长度关系曲线

以上通过AVP-970和美国MIL-STD-1797A两种工程估算方法，以及原准机类比法所求得的反尾旋伞特征参数比较接近，所以伞阻力特征值暂定为CDSD≈A m2，伞绳长度暂定为Lr≈Fm。为了有所比较另外设计了两个不同面积的伞，一个面积比A大，一个比A小；还设计了两个伞绳长度，一个比F大，一个比F小。

IRVIN公司的经验指出：为了避免估算反尾旋伞特性出现重大失误，必须谨慎使用上述公式，必须通过立式风洞试验或模型自由飞试验进行必要的验证，才能较好的确定伞的尺寸。

2.2 试验验证

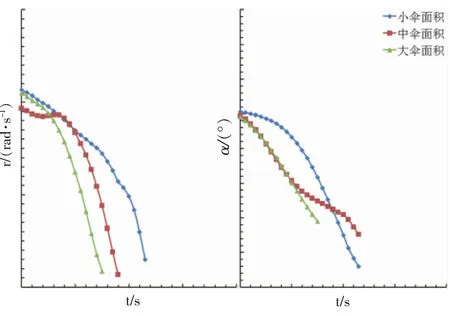
图9　伞面积大小对飞机尾旋改出影响比较

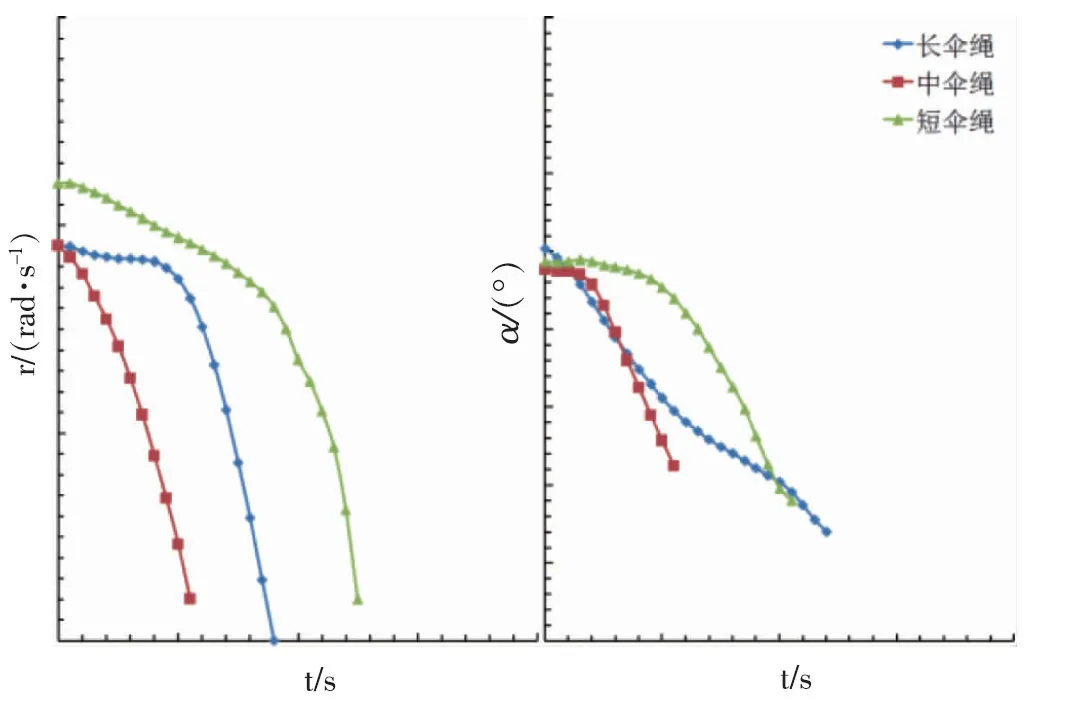
图10　伞绳长度对飞机尾旋改出影响比较

在尾旋风洞中进行的反尾旋伞选型试验结果如图9和图10所示。图9为不同伞面积大小对尾旋改出的影响，当使用大号伞攻角和偏航角速率降到零所需时间最短。可以看出随着伞面积的增大，改出效果越好，基本为单调关系。图10为不同伞绳长度对尾旋改出的影响，可以看出当使用中伞绳长度时，攻角和偏航角速率降到零所需时间最短，而使用长伞绳和短伞绳的改出时间较长，改出效果均不如前者。综合评价，选择最大伞面积的伞和中等长度的伞绳，尾旋改出的效果最佳。需要补充说明此一选择假定了飞机尾部强度满足开伞冲击载荷。

3　结论

通过系统的分析和研究，使用了一套适用于工程应用的预测飞机采用舵面组合法改出尾旋的方法，利用飞机模型的大攻角静态测力试验数据中各有关舵面偏转的气动力结果评判单独偏转舵面对尾旋改出能力的影响。利用美国NASA所使用的评判飞机尾旋改出的经验公式得出常规布局运输机改出尾旋主要依靠方向舵的偏转。最后在尾旋风洞中通过动态风洞试验进行了相关的验证，得出飞机A改出尾旋的最佳方法为反舵推杆法。此外，总结并利用国际上通行的反尾旋伞设计方法设计了不同规格的反尾旋伞，通过尾旋风洞试验对反尾旋伞进行了选型，通过试验结果分析，选择了最佳的伞面积和伞绳长度。在满足飞机结构强度的前提下，采用最大号面积的伞与中长度伞绳组合改出飞机尾旋的效果最佳。