大型飞机机身垂直入水冲击特性数值研究
2018-07-11刘沛清屈秋林
张 旭 刘沛清 屈秋林 /
(北京航空航天大学,北京100191)
[基金项目]本文受国家自然科学基金(11502012、11772033)支持。
0 引言
大型飞机水上迫降性能的研究[1-4]离不开对物体入水过程的研究。在飞机入水的过程中,会有很大的冲击载荷和冲击压强出现在结构上,同时后机身出现很大的吸力导致飞机出现大幅度的抬头。后机身的吸力主要是由于飞机水平方向的运动引起的,而冲击载荷和冲击压强主要是由于飞机的下降速度导致的。
影响物体入水冲击过程的因素有很多,譬如物体的几何形状、姿态和冲击速度等。大部分研究主要集中于轴对称或二维物体进入平静水面的过程。首先研究物体入水冲击问题的是Von Krmn[5],他在研究水上飞机的入水性能时使用动量守恒和附加质量法求解了二维楔形体入水的垂向载荷。随后,Wagner[6]考虑了水面抬升并通过扩张平板假设得出了更好的结果。Cointe、Armand[7]、Oliver[8]和Korobkin[9]等使用了匹配渐进展开法求解二维圆柱入水过程的载荷。Zhao等[10]使用边界元方法求解了二维楔形体和艏外飘截面入水过程中的水面形状、垂向载荷和压强分布。Mei等[11]采用了一种解析方法求解二维楔形体、二维圆柱和艏外飘截面入水过程中的载荷。Greenhow[12]、Sun和Faltinsen[13]采用边界元方法求解二维圆柱入水过程中的载荷,而Vandamme等[14]则使用了SPH方法来求解二维圆柱入水问题。王明振等[15]采用实验方法研究三种水陆两栖飞机典型横截面在不同投放高度和质量下的入水冲击中压强和载荷的变化。上述研究主要集中于楔形体、圆柱、艏外飘截面和飞机截面等二维物体的入水冲击过程。
三维物体入水问题的研究主要集中于航天器返回舱入水,而对于带中央翼盒的机身形状入水的研究很少。Mcgehee等[16]对Mercury返回舱的1/12比例模型以姿态角范围在-30°~30°之间的入水冲击载荷进行了实验和理论分析。Stubbs[17]采用Apollo返回舱的1/4比例模型实验研究了不同速度和姿态角的着水冲击载荷。Wang等[18]使用LS-DYNA研究了Apollo返回舱以不同姿态角入水过程中的加速度变化,结果发现Von Kármán方法低估了初始的冲击加速度而Wagner方法则出现了高估。以上的研究表明姿态角、速度和物体形状都会对入水过程产生影响,同时三维物体的形状复杂,将二维的结果直接应用到三维误差较大。
本文利用数值模拟手段,对带中央翼盒的细长体机身在不同姿态角、入水速度和机身尾翘角情况下的入水冲击过程进行数值模拟,通过研究各参数变化的影响规律,达到揭示机理之目的。
技 术 研 究
1 物理模型
图1为机身垂直入水的示意图。笛卡尔坐标系原点定义在初始的平静水面上,x方向平行于平静水面指向机身后方,y方向铅垂向上,z方向由右手螺旋定则确定;姿态角a是机身轴线与平静水面的夹角;x1和x2是机身的两个典型横截面;机身以恒定速度V向下冲击平静水面,入水后机身受到的垂向力Fy,机身浸没在平静水面下的浮力Fb,两者之差定义为机身受到的冲击力Fi。
图2展示了计算中的机身模型(参照某型飞机)。计算中采用1/10的缩比模型,计算模型的机身总长L=3.85m,后体长La=36.3%L,当量直径为D=0.31m。尾翘角分别为β=3°,5°7°,如图2(b)所示。图2(c)展示了不同姿态角(α=8°,12°)下的机身横截面形状,其中x1=2.1m处为中央翼盒的典型截面,x2=3.3m处为机身尾部的典型截面,可以发现它们的形状基本相似。

(a) 机身侧视图

(b) 后机身
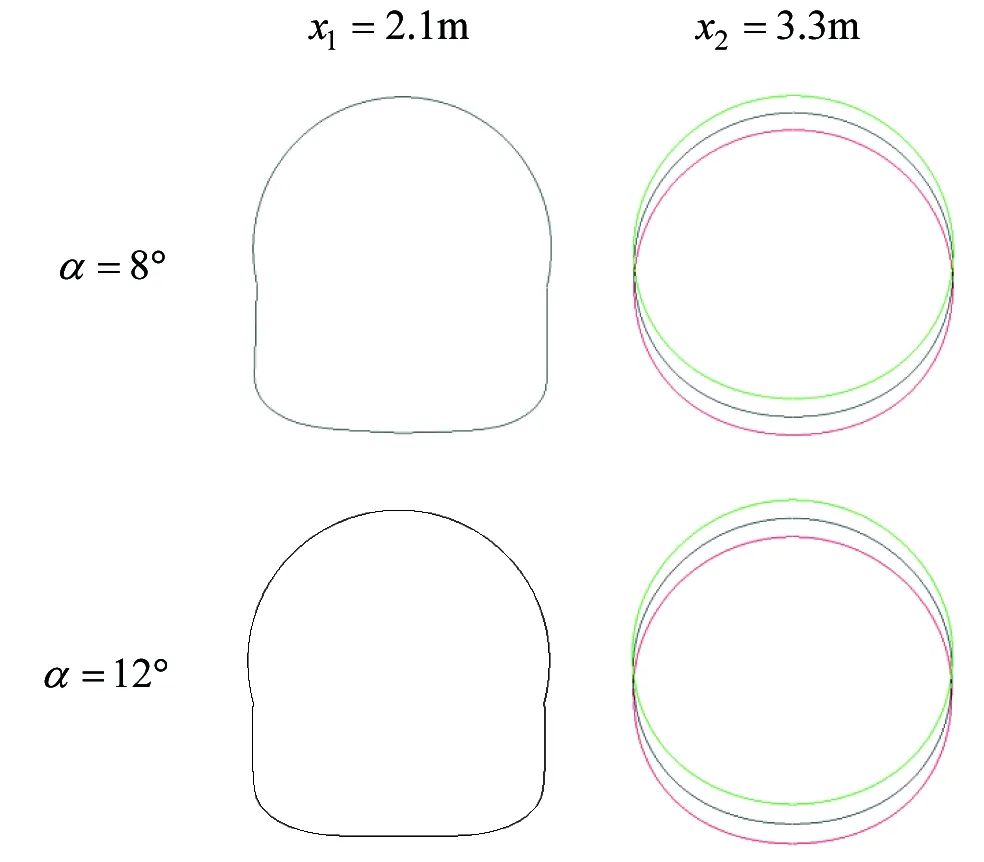
(c) 机身横截面形状图2 机身模型
2 计算方法和验证
2.1 流场求解
计算中采用ANSYS FLUENT 14.0双精度求解器来求解非定常可压缩的RANS方程,考虑了空气和水的重力。湍流模拟选取可实现的k-ε模型和加强壁面函数处理。压强速度耦合采用SIMPLE方法。对流项采用三阶MUSCL格式,扩散项采用二阶中心格式,非定常项采用一阶隐式格式。
2.2 自由面模型
自由面的捕捉采用VOF模型,模型通过对每一个相定义体积分数来模拟该相,每一个网格单元中所有相体积分数之和等于1。对于一个网格单元,q相的体积分数定义为:γq=0意味着该单元中没有q相;γq=1意味着该单元中充满q相;而0<γq<1表示该单元是相间的交界面。
第q相体积分数的连续方程为:
(1)
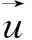
2.3 整体动网格技术
整体动网格技术(Qu等[19])用来模拟机身和水体之间的相对运动。计算过程中,整个计算区域及其内部的网格随着机身做刚体运动,这种方式不会出现网格的变形和重构,保证了网格的质量并节约了计算资源。
机身表面采用无滑移壁面边界条件;计算区域的边界为速度入口边界条件,边界上的体积分数设定可以保证在网格的运动中自由面保持不动。
图3是计算区域和机身附近的网格划分情况。计算中采用半模,计算区域大小为3L×2L×L,如图3(a)所示,其中xy平面为对称面。结构网格可以更好的捕捉水面,因而计算中采用了结构网格并对机身物面附近进行加密。图3(b)展示了机身附近的网格划分情况,最终采用的网格数量大约140万。
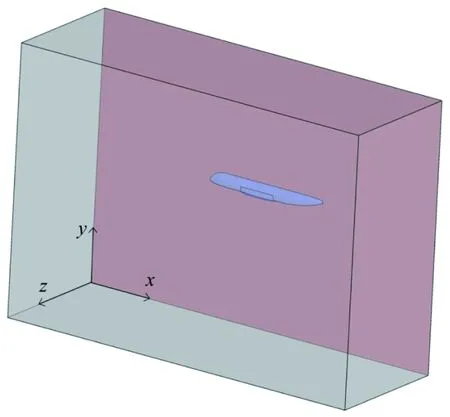
(a) 计算区域

(b) 机身附近网格图3 计算区域和机身附近网格
2.4 网格数量和时间步长的依赖性验证
选取尾翘角为β=5°的机身模型以α=12°姿态角,V=0.5 m/s下沉速度的入水过程,开展网格数量和时间步长的依赖性验证。
图4是70万(Coarse)、140万(Normal)和280万(Fine)网格数量计算的垂向载荷系数时间历程对比,其中S=π(D/2)2为典型机身界面的面积。可以看出70万网格与140万差距较大,而140万与280万差距较小,因此下文计算中选取140万网格是合理的。

图4 不同网格数量计算的垂向载荷系数时间历程
图5是Δt=10-3s、10-4s和10-5s时间步长计算的垂向载荷系数时间历程对比,可以看出时间步长为10-3s的结果与10-4s的结果差距较大,而10-4s与10-5s的结果差距较小,因此下文计算中选取的时间步长为10-4s。
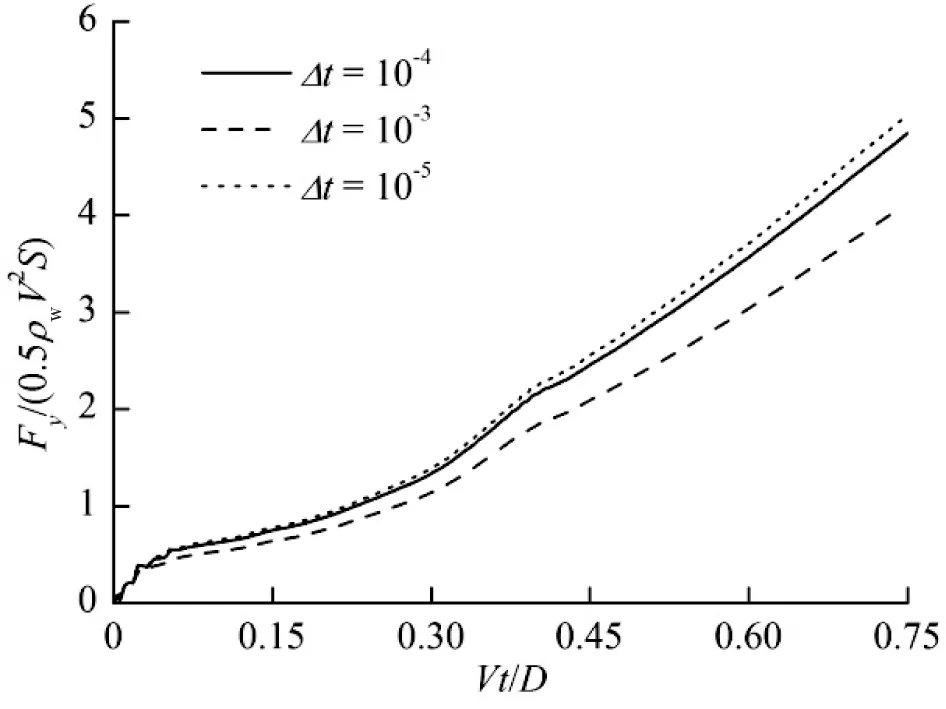
图5 不同时间步长计算的垂向载荷系数时间历程
2.5 计算方法验证
本文选取Lin和Shihe[20]的圆柱入水实验来验证本文计算方法的精度。实验中的压强传感器为Kyowa PGM-2KC(直径5.5 mm,频率24 KHz,量程2×105Pa),照相系统为CCD-16 MHz。圆柱材料为丙烯酸树脂,圆柱长度20 cm,直径20 cm,重量12.5 kg。自由降落的初始高度为0~20 cm,入水速度范围0.76 m/s~1.98 m/s。压强监测点相对于中心线的圆心角为0°、7.5°、15°和30°。验证选取入水速度为0.99 m/s的实验结果。计算中采用上述数值模拟方法对二维圆柱的入水过程进行模拟。
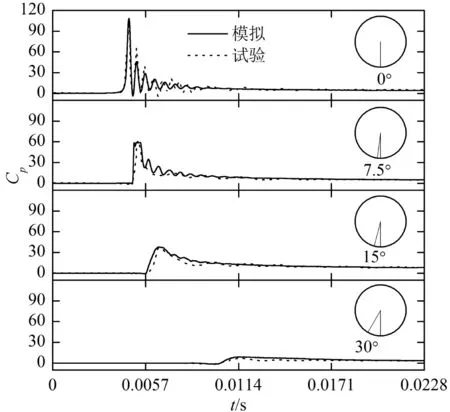
图6 实验和模拟的压强系数的时间历程对比
图6是实验和模拟计算的压强系数的时间历程对比。其中压强系数定义为Cp=(p-p0)/(0.5ρV2),其中p为当地压强,p0为大气压强,ρw为水的密度,V为触水时刻的速度。从图中可以看出模拟结果与实验结果的峰值和趋势都吻合得很好。实验结果中7.5°和15°中压强几乎没有波动而模拟中有波动,这个差异是由于实验中三维效应导致该位置没有空气泡出现,而二维计算模型中出现了空气泡。本文的数值方法可以很好地模拟入水过程。
3 计算结果与分析
为了研究入水速度、姿态角和机身尾翘角对机身垂直入水冲击过程的影响,计算了不同尾翘角(β=3°,5°,7°)的机身以常速度进入水体的过程,其中入水速度分别为V=0.25 m/s,0.5 m/s,姿态角分别为α=8°,12°。
3.1 典型的机身入水过程
选取尾翘角为β=5°的机身模型以姿态角α=12°,V=0.5 m/s下沉速度的垂向入水过程为典型算例。图7为该过程中的水面位置和机身腹部压强分布。
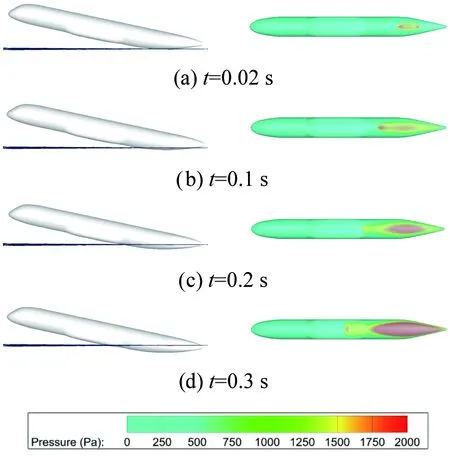
图7 典型入水过程(β=5°,α=12°,V=0.5 m/s)中水面形状和机身腹部压强分布
从图7(a)中可以看出在刚入水后不久的t=0.02 s,压强峰值很大且出现在喷溅根部。随着入水深度增加,压强峰值略有减小,且与底部区域的压强差距有所减小,如图7(b)所示。图7(c)为t=0.2 s时刻,此时压强峰值已经转移到了机身底部,而且水面已经到了中央翼盒的位置,导致局部的压强增大。从图7(d)可以看出,当机身浸没深度继续增加,压强峰值一直在机身的底部,同时由于冲击效应中央翼盒与水面接触的前部位置出现了局部的压强极大值。
在船舶研究领域,人们通常使用切片法,用纯2D物体的入水冲击特性代替3D物体截面的入水冲击特性。为了研究这种近似带来的误差,本文对比典型机身截面和形状相同的纯2D物体入水冲击特性的差别。
图8是入水过程中机身x2截面和2D物体的表面压强系数对比,其中y=0为初始时刻平静水面的位置。可以发现3D和2D的压强系数分布具有一定的相似性,而它们的差别主要来自3D的纵向流动和冲击。在图8(a)中的t=0.02 s时刻,压强系数峰值并没有出现在物面底部即y/D最小的地方,而是出现在水面附近的喷溅根部,由于存在纵向流动3D截面上的压强系数峰值小于2D;随着y/D继续增大压强系数迅速减小;最后y/D>0.1的部分是由于上方没有接触到水因而物面压强系数基本为零。随着入水深度的增加,在图8(b)所示的t=0.1 s时刻,压强系数峰值已经出现在了y/D最小的物面底部,由于纵向存在冲击这一时刻3D的压强系数峰值大于2D;随着y/D的增大压强系数迅速减小,在y/D=0.1附近出现了一些负压,这是因为冲击后出现了水面抬升,高于平静水面的水受到了重力作用;随后压强系数上升到零附近之后保持不变(y/D>0.3)。最后图8(c)中的t=0.3 s时刻,压强系数峰值也是在y/D最小的底部,此时纵向冲击影响减弱使得3D的压强系数峰值略小于2D;随后迅速减小直到零附近保持不变。
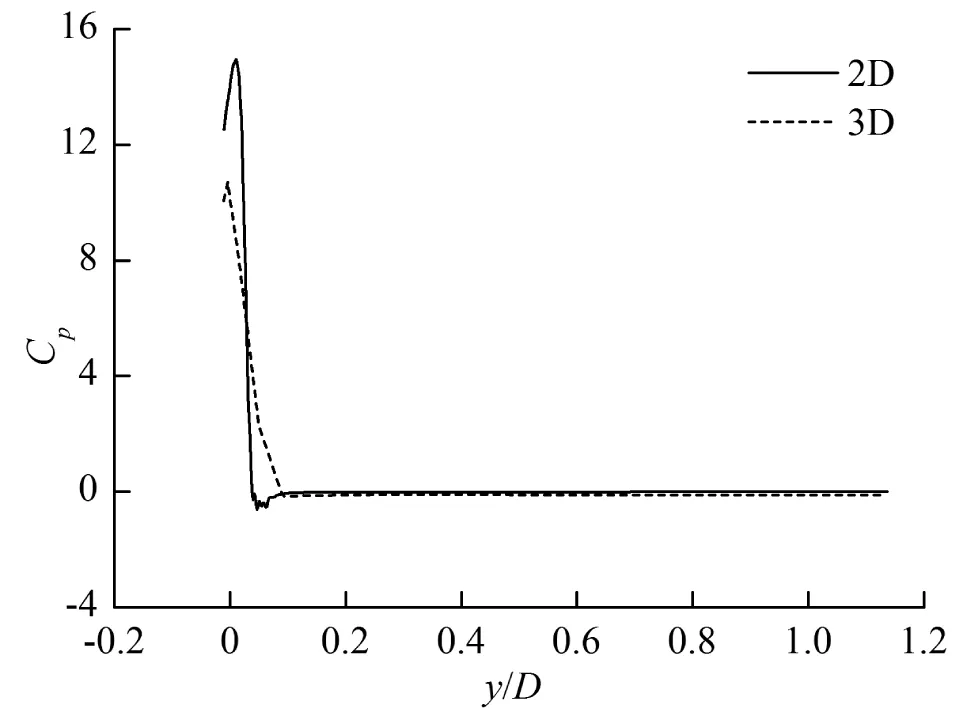
(a) t=0.02 s

(b) t=0.1 s

(c) t=0.3 s图8 入水过程(β=5°,α=12°,V=0.5 m/s)中机身x2截面和2D物体表面压强系数对比
图9是入水过程中机身x1截面和2D物体的表面压强系数对比。可以看出该截面上压强系数分布的变化规律与图8是基本一致的。在入水初期,如图 9(a)所示,3D与2D的压强系数峰值差别较大,这是由于此时的后机身大部分已经浸没水面,纵向流动的影响很大使得3D的压强系数峰值远小于2D。
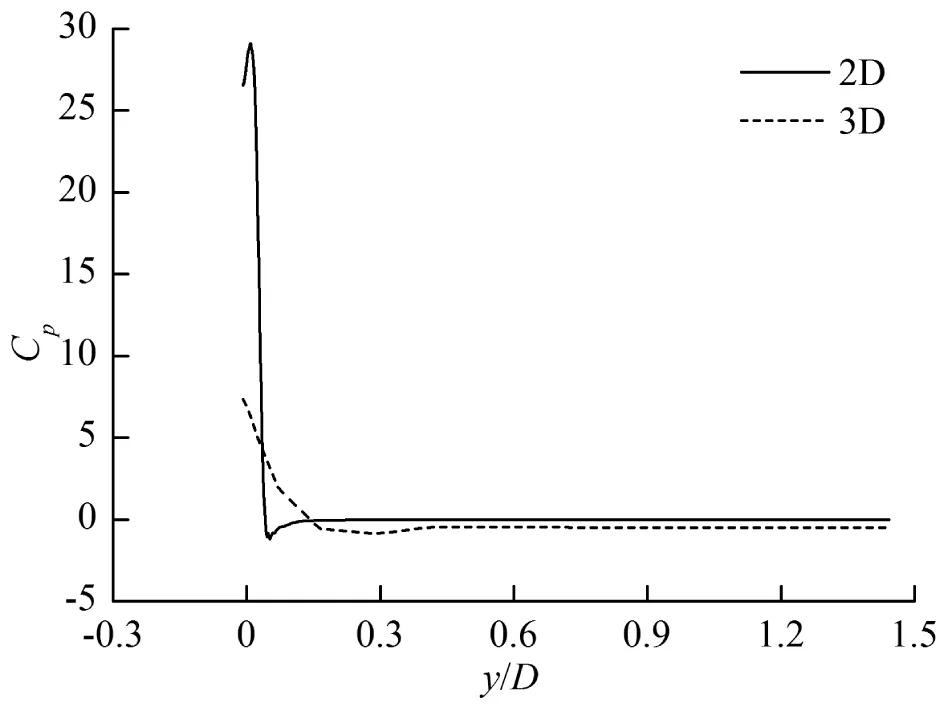
(a) t=0.34 s

(b) t=0.4 s
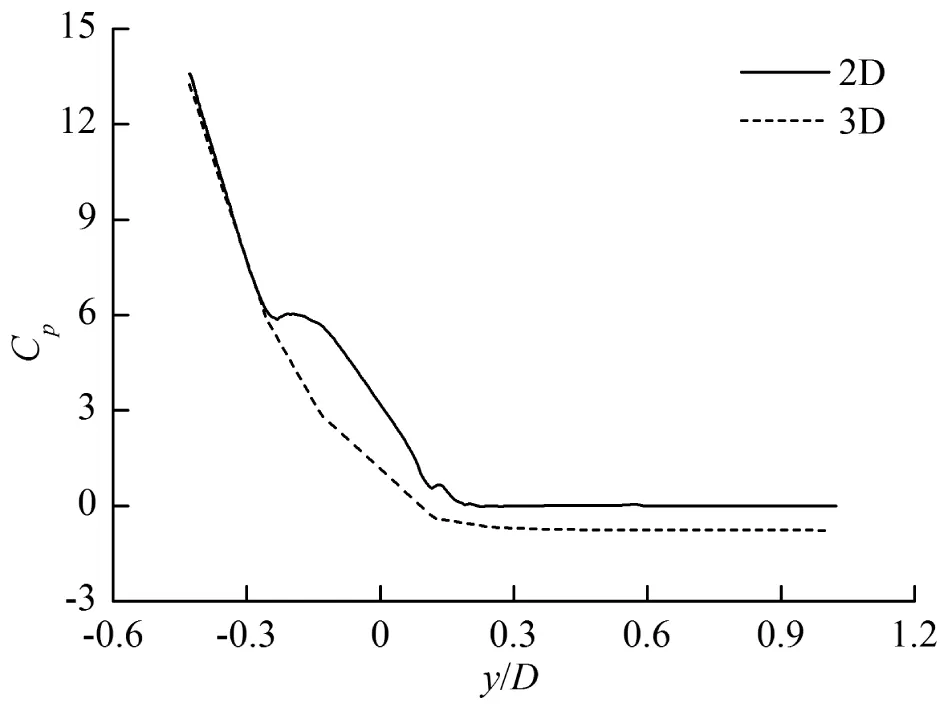
(c) t=0.6 s图9 入水过程(β=5°,α=12°,V=0.5 m/s)中机身x1截面和2D物体表面压强系数对比
3.2 入水速度、姿态角和尾翘角的影响
图10是入水过程(β=5°,α=12°,V=0.5 m/s)中机身冲击力Fi系数的时间历程。机身刚进入水面时(Vt/D<0.07),冲击压强很大,同时浸润面积迅速增加,导致冲击力系数迅速增大;随着入水深度的增加(0.07
可以看出,中央翼盒冲击水面前后冲击力系数发生了很大的变化,因而本文以中央翼盒冲击水面的时刻为界,将机身最低点触碰水面的时刻到中央翼盒触碰水面的时刻称为入水前期,之后为入水后期。

图10 入水过程(β=5°,α=12°,V=0.5 m/s)中机身冲击力系数时间历程
3.2.1 入水速度
图11为不同入水速度下(β=5°,α=12°,V=0.25 m/s,0.5 m/s)机身冲击力系数的时间历程对比。在同一无量时刻,入水速度较小时的浸润面积较大,导致冲击力系数较大。

图11 不同入水速度下(β=5°,α=12°,V=0.25 m/s,0.5 m/s)机身冲击力系数的时间历程
3.2.2 姿态角
图12为不同姿态角下(β=5°,α=8°,12°,V=0.5 m/s)机身冲击力系数的时间历程对比。入水初期,姿态角α=8°的冲击力系数比姿态角α=12°的略大,这是由于α=8°的浸润面积略大;在入水后期,由于机身以α=8°入水时中央翼盒冲击水面的时刻早于以α=12°入水的时刻,而且冲击水面时的底部抬升角较小,这导致以α=8°入水的冲击力系数峰值大于以α=12°入水的峰值。

图12 为不同姿态角下(β=5°,α=8°,12°,V=0.5 m/s)机身冲击力系数的时间历程
3.2.3 尾翘角
图13为不同尾翘角下(β=3°,5°,7°,α=12°,V=0.5 m/s)机身冲击力系数的时间历程对比。入水初期,尾翘角大的机身浸润面积较大,因而冲击力系数较大;入水后期,尾翘角大的机身的中央翼盒先冲击水面导致冲击力先变大,但由于冲击时的底部抬升角差别不大,因而冲击力系数峰值差别较小。
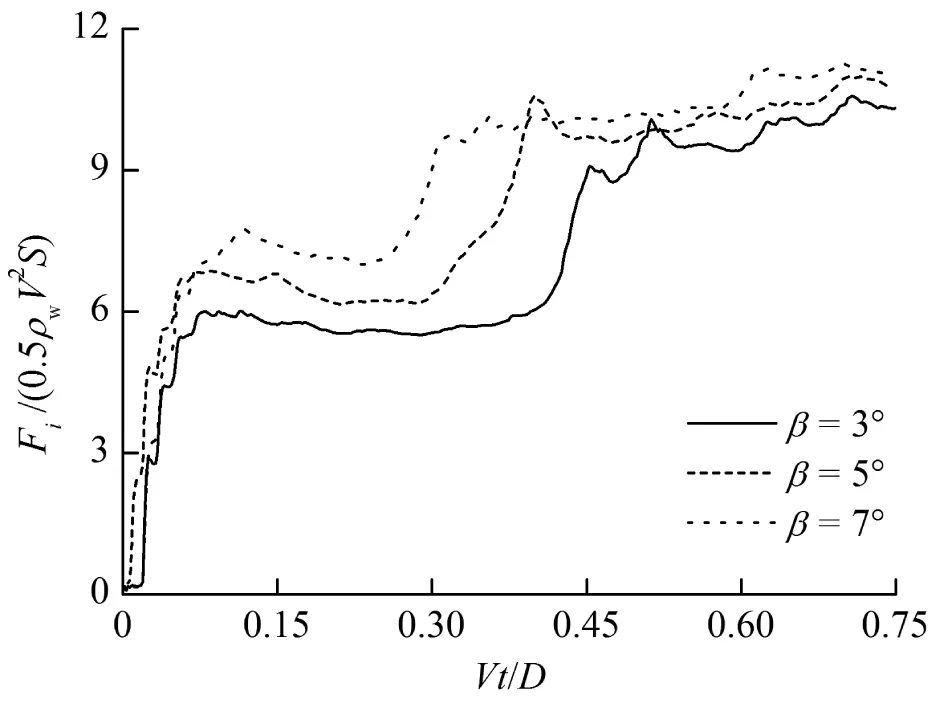
图13 不同尾翘角下(β=3°,5°,7°,α=12°,V=0.5 m/s)机身冲击力系数的时间历程
4 结论
本文通过数值模拟方法研究了不同尾翘角的机身以不同速度和不同姿态角的入水过程。结果分析表明:
1) 机身入水过程中压强峰值首先出现在喷溅根部,随后转移至机身底部。三维效应的影响表现为入水过程中机身截面的压强峰值先小于二维的峰值,随后大于二维峰值,最后又小于二维峰值。
2) 入水初期机身冲击力系数迅速增大,而后略有回落,入水后期由于中央翼盒冲击水面会导致冲击力系数再次迅速增大,而后小幅震荡。
3) 速度越大、姿态角越大、尾翘角越小,机身冲击力系数越小。
