泳池中盘制漩涡对的形成与稳定
2018-07-11王盟航王志铖李山东省青岛第二中学山东省青岛第二中学物理组山东青岛66000
王盟航王志铖李 鹏(山东省青岛第二中学;山东省青岛第二中学物理组,山东 青岛 66000)
漩涡现象是我们生活中的一种常见现象。例如,当一艘货轮缓慢地离开港口时,它船体的两侧就会产生许多微小的漩涡;当我们把洗手池中的塞子拔掉的时候,水体的运动也会转化成一种漩涡运动的形式;当我们以一个适当的力度向前推一个装有半瓶水的瓶子时,水中会形成“龙卷风”,但最终又会衰减。
最近,我们发现将盘子在游泳池中推动时(图1),一对漩涡可以在盘子周围产生(图2)。将盘子向前推一段路程后抽出,几分钟之后,漩涡仍然存在,并能稳定地向前运动。这对保持长期稳定状态的漩涡引起了我们的兴趣。后来,我们重复了此实验,漩涡生成且保持稳定。为什么这样一对漩涡能在没有外界能量加入的情况下稳定地存在呢?
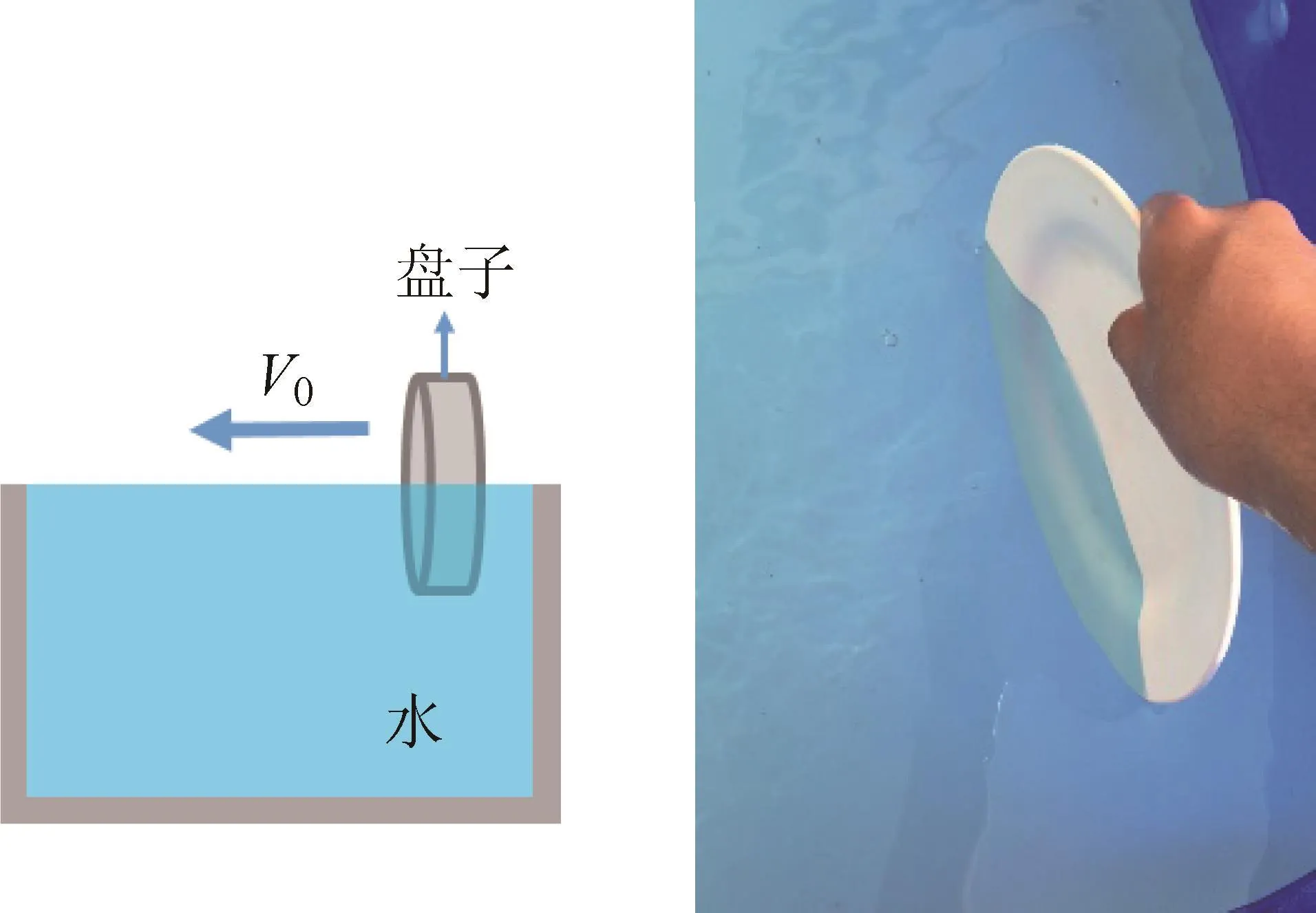
图1 推盘子侧视图

图2 抽出盘子后形成的一对漩涡
1 流体问题的前提假设
1.1 漩涡形成模型的流体特点
研究流体问题,首先要确定流体的模型,要从粘性和压缩性两点来考虑。
盘子在水中运动时,盘子物面将对流体产生阻力。因此,在盘子物面和远离盘子的来流区域处产生速度差,导致粘性应力产生。黏性应力的作用造成了流体垂直于盘子方向的流动和漩涡的形成。同时,根据达朗贝尔佯谬[1],当物体对流体产生阻力时需要考虑黏性。
由于推盘子的速度小于5 m/s,不会对液体压缩做功,所以在此流体模型中,水为不可压缩流体。
综上,漩涡形成模型的流体特点为黏性且不可压缩。
1.2 漩涡稳定模型的流体特点
当盘子抽出水面之后,物面产生的黏滞阻力消失,此时,黏性作用可以忽略。同时,流体未受外力做功,流体模型亦是不可压缩流体。
综上,漩涡向前运动时的流体特点为非黏性且不可压缩。
1.3 变量表格

变量名称 变量含义τ黏性应力μ沿x轴来流速度U0外部流动区域来流速度δ边界层的厚度v沿y轴来流速度ρ流体密度ν液体动力黏滞系数l特征长度(盘子的弦长)p液体压强g重力加速度常数ω涡量Γ环量L积分路径R单个漩涡半径U推动盘子的速度r距离矢量θ液体黏性系数u漩涡的角度
2 理论模型
2.1 漩涡形成模型
在实验中,我们以流体为坐标系,通过让盘子在水中移动一定距离产生漩涡。现在,我们把坐标系建立在盘子上(图3)。假设盘子固定不动,流体向盘子方向流动。(风洞测试飞机模型运用了同样的等效法)

图3 盘子坐标系示意图
2.1.1黏性应力
当部分插入水中的盘子遇到来流速度为U0的水时,由于受到盘子物面摩擦的影响,来流速度在盘子边缘上等于零,此时,远离盘子物面的速度是U0。因此,在盘子边缘和流速为U0的流体之间会产生速度梯度,进而产生黏性应力τ。

2.1.2边界层
为了进一步探究黏性应力对流场分布的影响,我们需要引入一个边界层的概念。边界层是指介于来流速度为零的区域(盘子边缘)和来流速度为U0的区域之间的区域。边界层同时是紧贴物面且非常薄的一层区域(图4)。
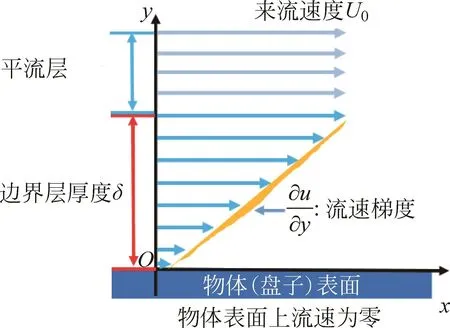
图4 边界层示意图
在远离盘子的平流区域,黏性力远小于惯性力,可以忽略黏性。但由于边界层内存在很大的速度梯度,黏性应力的作用效果明显,黏性力和惯性力作用同等重要。因此,漩涡将会在狭小的边界层内部产生,边界层内部的情况是我们研究的重点。
纳维 斯托克斯方程是用来描述黏性流体的,但是,边界层厚度δ比特征长度l(指盘子插入水中后,盘子表面与水面相切的弦长)小得多,我们可以简化纳维 斯托克斯方程,并将其推导为普朗特边界方程。
根据之前的分析,我们可以得到边界层方程的基本假设为
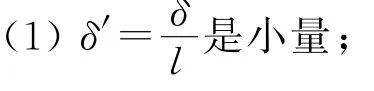
(2)黏性力和惯性力同阶。
我们通过估阶的方法将方程简化[2]。
纳维 斯托克斯方程

普朗特边界方程
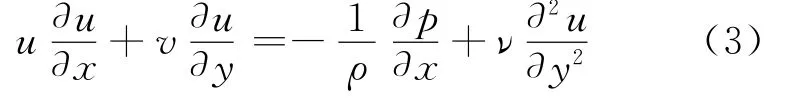
2.1.3边界层分离
现在,我们用边界层分离来解释漩涡对的产生。在盘子的物面上,黏附条件为
u=0, v=0
联立方程(4)和盘子物面黏附条件,可以推出:

联立方程(4)和黏度系数与动力黏度系数换算公式

可以推出方程
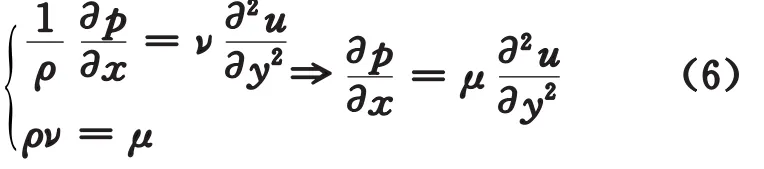
在方程(6)中,得到了压力导数和速度曲线曲率的关系,这将便于下一步分析物面周边流体速度场的变化。
我们先简化盘子模型为圆柱模型来分析边界层的分离过程。在圆柱上建立坐标系,利用LBM(Lattice Boltz mann Method)在Matlab中模拟边界层在圆柱物面的脱离过程。图5中展示的是圆柱周边流体的速度场,Re=100。

图5 Matlab圆柱物面边界层分离模拟
根据伯努利方程,可以通过模拟得到的速度场来推导圆柱周边压强场。

在图6中,深黑色箭头实线为添加的辅助线,用来表示来流方向。A、B、C、D 4个点代表圆柱周边特定位置的流体。

图6 圆柱物面边界层分离注释
A点位于圆柱前段,流速趋近于零;B点位于圆柱一侧,存在流速。此时,A点压强将大于B点压强,从A点到B点,压强减小,流体质点顺压强梯度流动,沿A点流向B点,且沿x轴方向的压强的导数小于零。

此时,根据方程(6),可以得出边界层内部速度曲率小于零,速度曲线沿y轴上凸,来流方向继续保持原先方向,没有发生回流。

图7(a)中的浅色线条展示的是此时边界层上的速度曲线,速度曲线在物面一侧没有发生变化,边界层此时紧贴物面。
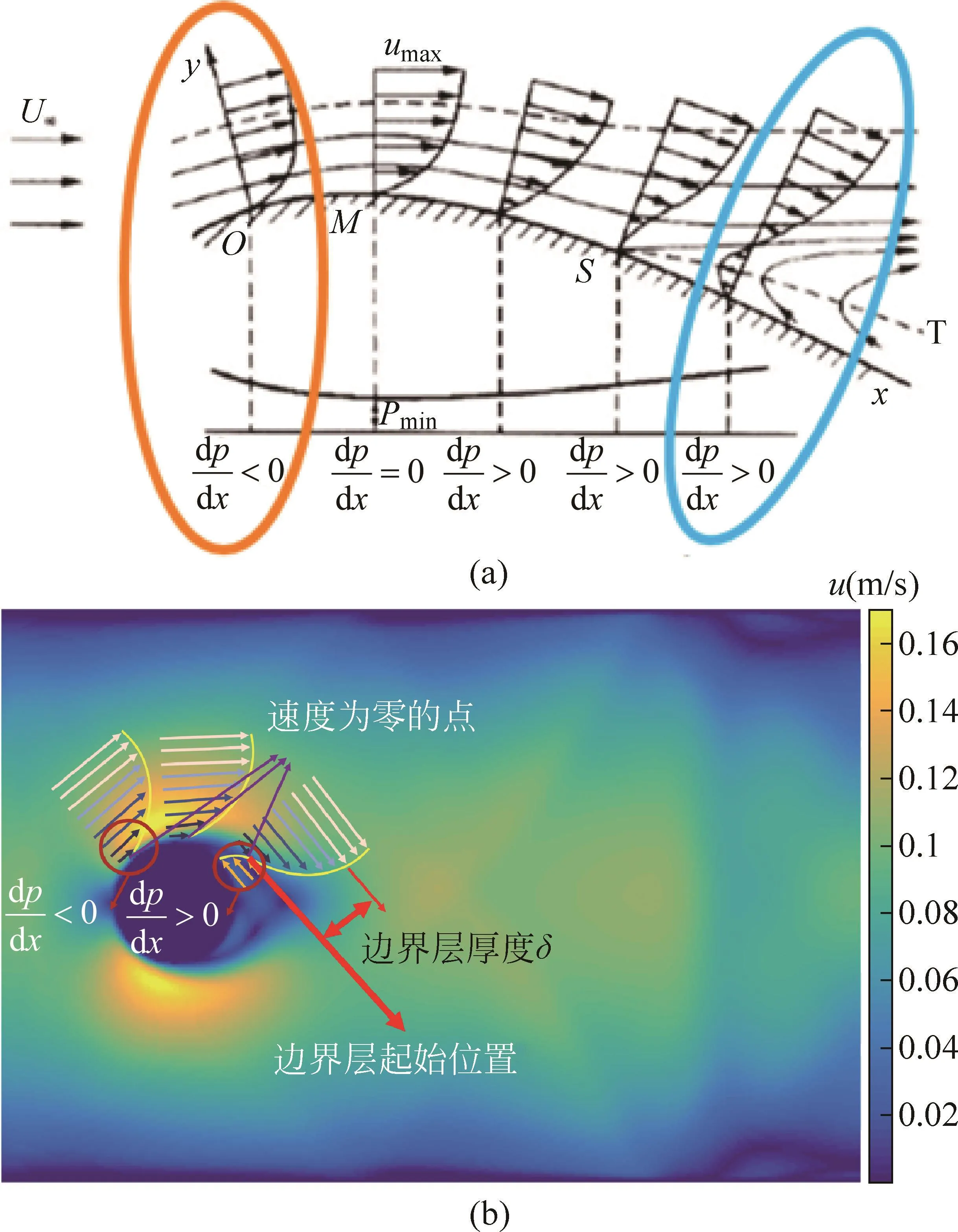
图7 圆柱物面边界层内速度曲线变化
回到图6中,C点位于圆柱背侧,流速趋于零,小于B点的流速。此时,从B点到C点,压强增大,流体质点逆压强梯度流动,因此沿着x轴的压强梯度大于零。
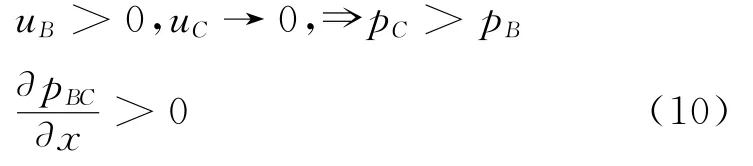
此时,根据方程(6),可以得出在边界层内部速度曲率大于零,临近物面一侧的速度曲线沿y轴下凸,来流方向继续与原先方向相反,发生回流。

此时,图7(a)中的深黑色线条表示盘子物面一侧的速度曲线反曲,物面附近速度不为零,边界层发生分离。
根据Matlab对漩涡速度场的模拟,我们发现圆柱绕流后速度分布发生了变化。速度为零的点(边界层起点)不在圆柱体的物面上,物面附近发生回流,边界层发生了脱离。图7(b)中的速度曲线的标注和速度场的分布展示了漩涡成因。此时位于圆柱两侧,一对漩涡将会在流体经过圆柱绕流后出现。
2.1.4盘子模型的修正
先前我们采用圆柱模型简化了盘子模型,因为盘子本身形状的特殊性,现在需要对模型进行修正。
同样,在盘子上建立坐标系。此时A点到B点在x轴方向的投影远小于圆柱上从A点到B点的投影,可以推出盘子模型沿着x轴的压强变化率将远大于圆柱模型。B点到C点的压强梯度同理可得。

因此,盘子模型产生的速度曲率变化相比圆柱模型会更加明显,使得流速为U0的流体在接触到盘子边缘的同时就发生边界层分离现象,使得漩涡对随后产生(图8)。

图8 Matlab盘子边缘边界层分离模拟
通过改进Matlab的代码,我们用盘子模型对边界层分离现象进行模拟,证实了接触盘子边缘的同时就会发生边界层分离,且产生更明显的漩涡对。
2.1.5回流区域验证
使用Fl uent编程设置盘子与平稳来流,模拟了盘子周围的流场分布。图9中箭头表示每一流体质点的速度矢量。Fl uent模拟证实了在紧贴物面的区域,速度矢量发生变化,物面附近流体速度不为零且与来流速度U0方向相反,形成漩涡结构。
2.2 漩涡U形涡管稳定模型
2.2.1U形结构的形成
之前我们只对漩涡进行了二维的研究,现在需要进一步探究这对漩涡在流体中的三维结构。
由于部分盘子是浸在水中,运动的流体与盘子物面接触时,在盘子的半圆形边缘上均会发生边界层分离,并产生湍流和漩涡现象。因此,漩涡会沿着盘子浸入水中的边缘形成(如图10所示)。
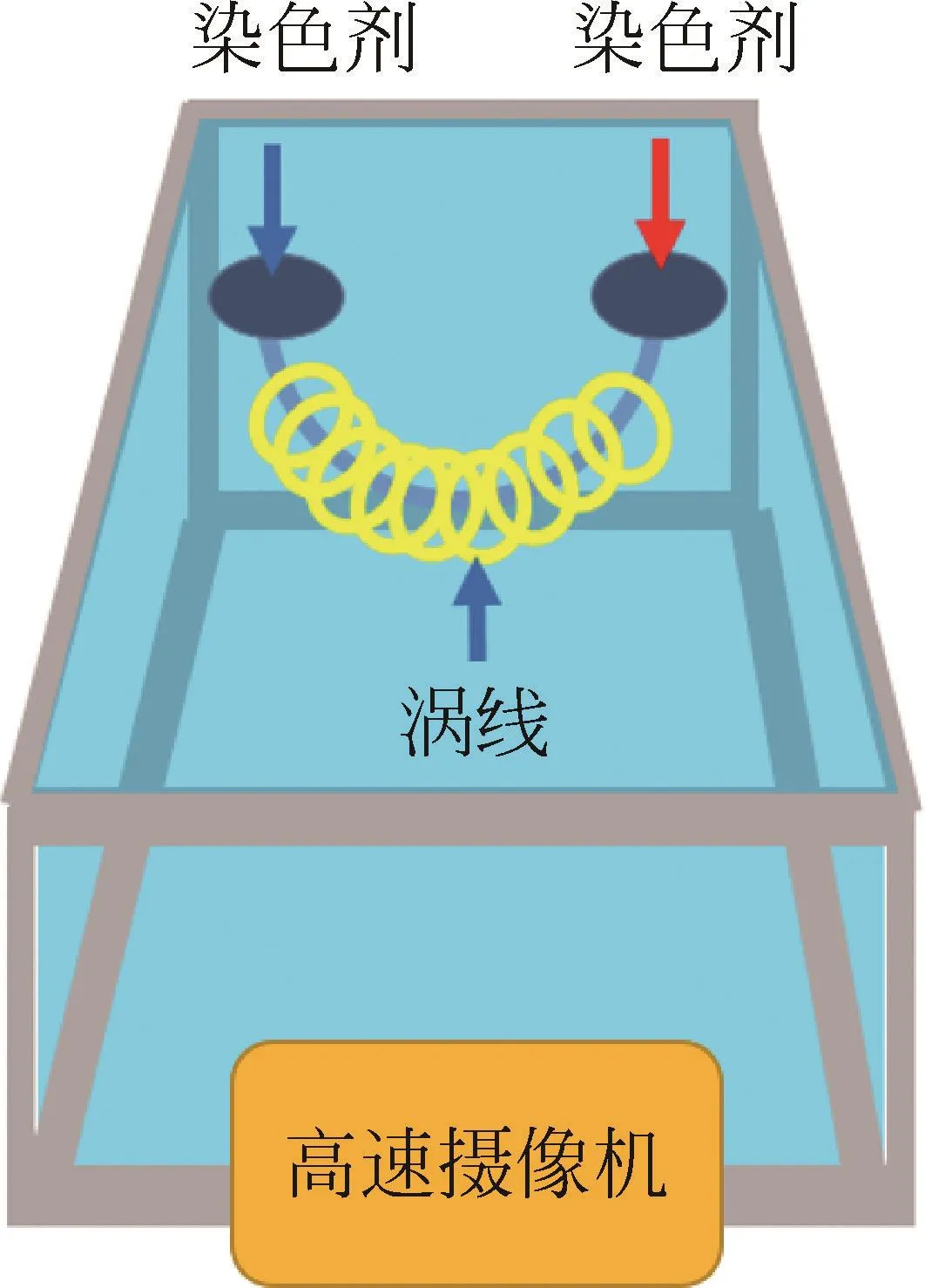
图10 漩涡U形结构示意图
这些连续在盘子边缘的漩涡将最终形成U形的联通结构。利用染色剂对其进行染色(如图11所示),发现染料能沿着U形结构从一个漩涡中心,向另外一个漩涡中心输送,反之亦然;同时,染料跟随漩涡的U形结构一同向前运动。

图11 漩涡U形结构实际染色图
染色实验说明了U形结构的性质不是一种波,而是具有传递物质性质的结构。与此同时,我们曾试图故意破坏漩涡的U形结构。例如,在水池中央树立一根粗杆(直径3c m),当漩涡对从粗杆中央经过时,U形结构会因为粗杆物面产生的阻力而断裂,这一对漩涡发生能量耗散,并逐渐解旋并消失。
这个特殊的U形结构可能是保持漩涡稳定的重要条件,通过查阅相关资料,推断此结构可能为漩涡的涡管。
因此,接下来将要验证漩涡U形结构是否为涡管,同时建立漩涡漩涡U形涡管稳定模型。
2.2.2漩涡行进状态的流体模型
当利用盘子在水池中产生漩涡后,我们通过机械臂的电磁铁将盘子抽出,漩涡对会一同以一个几乎恒定的速度向前运动。此时,物面从流体中消失,边界层不再存在,惯性力远大于黏性力,漩涡达到一种稳态,可以忽略流体的黏性作用。
在纳维-斯托克斯方程中,

ν∇2u是黏性项,ν是流体的动力黏滞系数,速度场的矢量拉普拉斯是

漩涡引发的速度场是螺线型的,即∇·u=0,因此∇(∇·u)=0。另一方面,在漩涡的涡丝模型中,涡丝以外流场的涡量是零,所以∇×ω=0。此时黏性项就可以从纳维 斯托克斯场方程中消除掉,故我们可以把涡丝在流体中的运动看作是没有阻力且液体无黏性。
2.2.3涡量
对于流体中的漩涡来说,最关键的物理量是漩涡的涡量:ω=(ξ,η,ζ),涡量为速度场的旋度。ω=∇×u
根据亥姆霍兹第一定理[2],漩涡涡丝上的每一点都与涡量向量平行,因此满足方程:

通过扩展这个定理,可以解释染料沿涡丝传递并绕着涡丝中心旋转的原因;此推论也证实了涡丝是在流体中跟随漩涡一同向前运动,而不是向前或向外扩散。
漩涡通常由多条涡丝围成的一个闭合的曲面构成涡管(如图12所示),若涡管存在涡量,同时涡量处处相等,即形成稳定的涡管结构,那么这个漩涡将是稳定的。

图12 涡管示意图
2.2.4U形涡管稳定模型
速度环量Γ是指沿着一个闭合曲线c速度的线积分;根据斯托克斯定理,速度环量和涡量之间还有如下关系

这里的速度环量表示为漩涡的涡管强度。我们将这对漩涡的三维结构取出(即为图12)并计算它的速度环量,再把原式转化成体积积分的形式
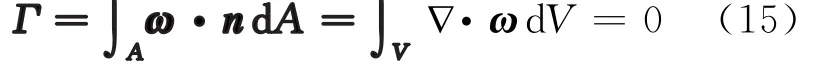
我们得到对涡管体积积分的结果是零。
再将漩涡的涡管强度利用涡管的3个表面(α面、β面和侧面)的速度环量的和来表示
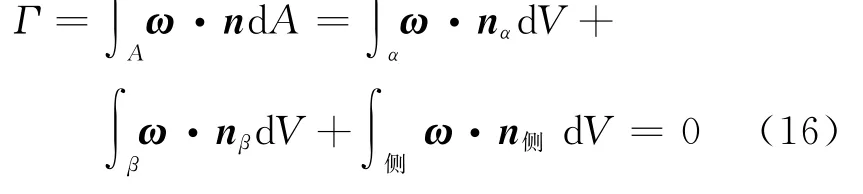
因为侧面速度环量为零,可以得到

根据α面、β面的法向量的关系为

可以得到:再漩涡涡管的横截面上,涡量处处相等。
同时,无黏性流体的涡旋管强度不随时间的改变而改变,所以涡量在漩涡运动过程中保持恒定。

这类涡管模型完全符合泳池中漩涡对的运动状态和自身特点。
将涡量处处相等进一步推广可得:一个涡旋的涡管不能以一端无限小的形式存在,否则它的涡量将无限大,所以涡管必须向两端延伸至水面的边界(泳池中的漩涡对)或者形成闭合的环(空气中的烟圈)。
根据我们用盘子制出的一对漩涡的形态来看,它形成的涡管结构是向两端延伸至水面的结构(图12),因此,这类涡管结构是这对漩涡能够稳定存在的原因。
2.3 漩涡存在特点
通过进行PIV实验,我们用CCD相机记录了漩涡在一个流体切面上的流场分布和速度场分布的情况,并探究漩涡存在时的速度场特点
漩涡的速度场和漩涡的涡量场是相互关联的。定义上,漩涡速度的旋度即是涡量。另一方面,我们推断漩涡的涡量场能通过毕奥 萨伐尔定律推导出漩涡的速度场。这个推断是由分析PIV实验得到的漩涡流场图像和在Mathematica中对半圆形通电导线的磁场进行数值积分的结果对比得来。这对漩涡的U形涡管附近产生的速度场u的速度环量Γ(图13(a))与半圆形电流强度为I的通电导线产生的磁感应强度B(图13(b))非常相似。
方程(17)将速度与速度环量联系:

安培定律将磁感应强度和电流联系:
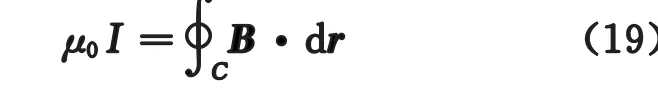
我们利用毕奥 萨伐尔定律推导漩涡速度场,即是漩涡的引发速度场:

在方程(20)中,d l是涡管的一小段,Γ是涡管强度,是由漩涡形成时的初始条件决定的。下面进行积分
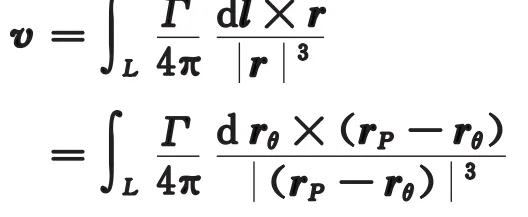
rP=(x,y,z)是流体质点P的位置,

从图13的对比结果中,看出漩涡对的速度场和半圆形通电导线的磁场非常相似。

图13 漩涡对的速度场和半圆形通电导线的磁场
3 实验装置
3.1 实验设备
(1)PIV(particle image velocimetry)粒子示踪技术。PIV设备使用CCD工业相机,PIV粒子水和3瓦绿色激光器组成。示踪粒子浮在水中的各个层上,当有流体运动时,粒子的轨迹便可以记录漩涡的流场、速度场。
(2)机械臂。利用步进电机、CCM直线导轨、工业自动化控制器等设备组成机械臂运动单元,步进电机结合伺服电机精确控制盘子向前移动的速度和加速度。同时利用弹簧、电磁铁、电磁继电器和导轨制成盘子回收装置,以保证漩涡生成后盘子能被及时并且竖直抽出,减少人手产生的实验误差。
3.2 实验方法
利用激光器产生扇形激光平面照射在PIV粒子水中,产生漩涡后,利用CCD相机(20 ms/张)记录PIV粒子的运动情况。

图14 实验设备
3.3 预实验

图15 机械臂
我们进行预实验来描绘机械臂的速度曲线,从而测试机械臂的速度控制是否精确。利用激光器产生扇形激光平面照射在PIV粒子水中,产生漩涡后,利用CCD相机(20 ms/张)记录PIV粒子的运动情况。
4 实验结果
4.1 漩涡的前进速度
图16展示了漩涡向前运动时的位移 时间图像,通过Origin进行线性拟合,我们得出漩涡向前运动的速度是一个定值,验证了之前的假设,即漩涡在运动过程中,周围流体对于漩涡来说是无粘的。
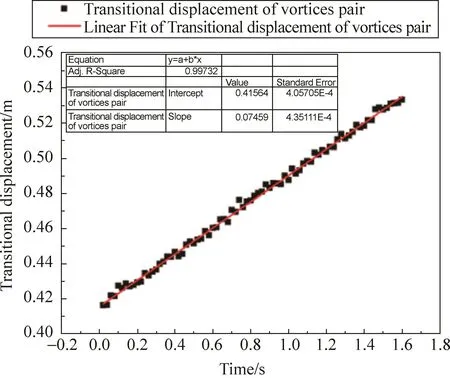
图16 漩涡前进位移—时间图
4.2 漩涡的平均动能
图17展示了漩涡向前运动时平均动能的变化。从中发现,漩涡动能在减少,漩涡在耗散。但是,漩涡的扩散几乎是稳定的,漩涡的衰减是很小的。
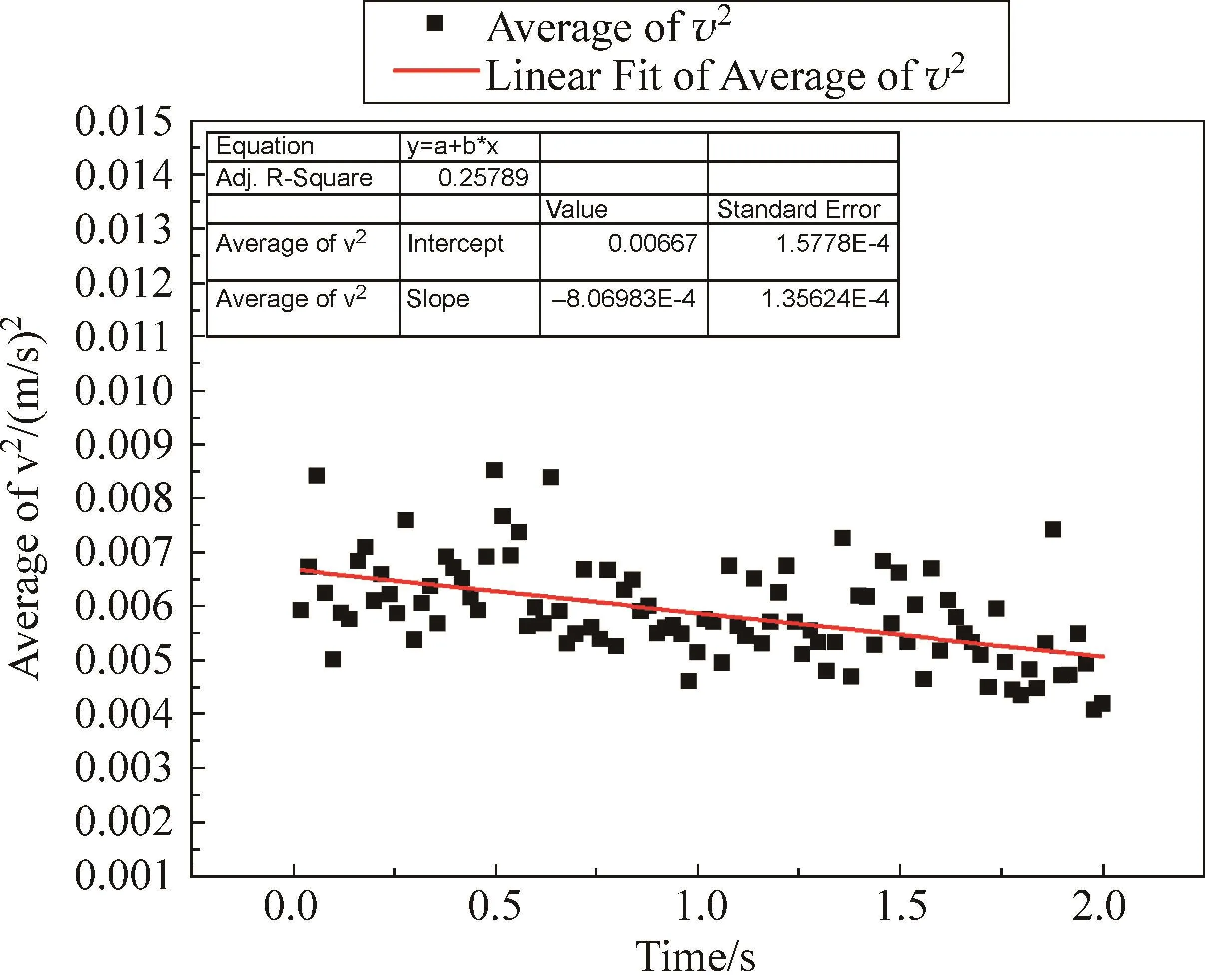
图17 漩涡平均速度平方—时间图
4.3 漩涡的涡量
图18展示了漩涡向前运动时漩涡的涡量变化。漩涡涡量在减小,说明漩涡的稳定性在下降。同漩涡的平均动能一样,涡量减少很小,所以漩涡能保持稳定很长时间。

图18 平均涡量(绝对值)—时间图
5 总结
5.1 漩涡的形成
通过简化纳维 斯托克斯方程得到普朗特边
界层方程,我们推导并解释了为何在大Re数情况下,边界层内的速度曲率发生变化,物面上的边界层会发生分离,使得漩涡产生。通过计算机模拟软件Matlab和Fluent,我们对模型进行了修正,并对理论中提出的回流区域进行了验证。
5.2 漩涡的稳定模型
通过计算简化的纳维 斯托克斯方程,证明在漩涡对向前运动时,粘性作用可以被忽略。通过研究涡旋对的U形结构,并利用涡管的模型解释了漩涡对的U形结构,证明了涡量在涡管上处处相等,同时,涡管也是漩涡对保持稳定而不迅速耗散的原因。
5.3 漩涡的存在特点
利用毕奥-萨伐尔定律的形式对漩涡对的速度场进行积分,同时利用Mathematica对半圆形通电导线的磁场进行模拟,发现漩涡的速度场和半圆形通电导线产生的磁场有极大的相似性,进一步说明了漩涡的引发速度场可以通过毕奥 萨伐尔定律推导,方便了我们分析漩涡的速度场。
5.4 漩涡的运动特点
从PIV实验得到的实验数据和图像中,分析了漩涡的运动模式,发现漩涡前进速度保持恒定,且耗散很小。
