特种设备表面电刷镀层厚度的超声波评价研究

盖晓东 胡庆贤

（1.厦门市特种设备检测研究院 厦门 361004）

（2.江苏科技大学 材料科学与工程学院 镇江 212003）

电刷镀技术是一种广泛应用于特种设备零部件（如锅炉、重型机械等）表面修复与强化的表面工程技术，由于该技术具有使用方便、操作灵活、可在复杂形状工件表面进行刷镀等优点使得该技术在工件表面的修复、尺寸补偿（由腐蚀、磨损等引起）等领域得到了广泛关注[1-3]。镀层厚度是保证修复后工件尺寸的重要因素，因而如何对镀层厚度进行评价对保证修复质量就显得非常重要。金相观察法是目前常用于镀层厚度测量的一种方法，但由于该方法是在破坏试样完整性的基础上实现镀层厚度评价的，因而并不适于对刷镀期间以及所有刷镀工件镀层厚度进行评价，这也就使得寻找可对镀层厚度进行无损表征的方法对推广电刷镀技术在机械零件表面修复与强化中的应用显得极为重要。

瑞利波[4]又称表面波，是沿工件表面传播的一种超声波，由于它具有使用方便、安全、无辐射、检测范围广等优点，因而在无损检测领域得到广泛应用。文献[5]表明，在瑞利波检测范围内，瑞利波信号只与其检测深度范围内材料的特征参数有关，即随着电刷镀层厚度的改变，在电刷镀层内的瑞利波信号也会发生相应的变化，因而如何对携带与镀层厚度有关信息的瑞利波信号进行分析处理并提取出可用于评价电刷镀层厚度的参量对实现电刷镀层厚度的无损评价就显得非常重要。针对这一问题，本试验在45钢表面制备出厚度不同的电刷镀层，采用双瑞利波探头对其进行检测，在互相关函数[6]计算信号间时间差的基础上得到镀层厚度-时间差关系曲线，并通过幂函数拟合函数得到可用于评价镀层厚度的公式。

1 信号分析处理方法

根据瑞利波在介质中传播规律可知，当瑞利波检测范围大于电刷镀层厚度时，随着镀层厚度的改变，瑞利波在电刷镀层中的传播速度会发生相应的变化，但由于瑞利波波速对镀层厚度的改变并不敏感，以及由于“噪声”[7-8]信号对瑞利波信号的影响，因而，采用何种信号分析方法对电刷镀层瑞利波信号进行处理对保证镀层厚度评价结果就显得非常重要。互相关函数法是目前众多计算信号间微小时间差方法中的一种，由于它具有抗白噪声干扰能力强，算法简单等优点，因而在微小时间差计算领域得到广泛关注。文献[9-12]表明，互相关函数法是在估算波形相似程度的基础上计算信号间微小时间差的一种方法，见式（1）。

式中：

x(t)，y(t)——在不同厚度电刷镀层试样中传播的瑞利波信号；

τ——信号间时间差。

根据式（1）可知，x(t)，y(t)信号幅值不同时，互相关函数值Rxy(τ)也不同，而由于“噪声”对电刷镀层瑞利波信号的影响，本试验中瑞利波检测信号幅值并不相同，因而为了便于计算结果的对比分析，本试验在互相关函数的基础上对其进行离散归一化处理并得到互相关系数函数，见式（2）。

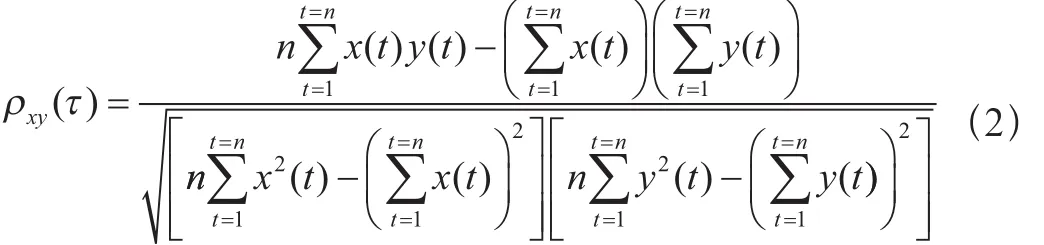
式中：

n——参考函数步长。

2 试验结果及分析

2.1 结果及理论分析

图1是采用电刷镀在45钢表面制备得到的厚度分别为62、70、78和90μm的电刷镀镀层金相组织。

为了避免瑞利波传播声程的改变对评价结果的影响，本试验采用中心频率为5MHz的一发一收模式的双瑞利波探头对不同厚度的电刷镀试样进行检测，结果如图2所示。

图1 不同厚度电刷镀层的金相组织

图2是厚度分别为62、70、78和90μm时电刷镀层试样的瑞利波信号。根据图2中瑞利波信号可知，随着电刷镀层厚度的增加，瑞利波信号逐渐向右移动，而由于瑞利波在电刷镀层中的传播声程以及始波位置固定不变，这也就表明，随着电刷镀层厚度的增加，瑞利波通过相同距离所用的时间逐渐变长，即传播速度逐渐变小，但其变化速率并不相同。对比不同厚度电刷镀层的瑞利波波形可知，瑞利波在镀层中传播一定距离后，波形会发生一定的“畸变”。对其分析认为这主要是由于电刷镀技术是以“尖端放电”效应[13]为理论基础，通过镀液中金属离子在基体表面沉积而得到金属镀层的一种方法，而由于金属离子沉积速率不同，因而镀层组织较疏松，即镀层中存在较多“孔洞”，如图3所示。根据瑞利波在介质中传播规律可知，瑞利波会在声阻抗不同的物质所形成的界面处发生反射、散射等现象，并形成干扰信号即“噪声”，从而使原有信号波形发生一定程度的“畸变”，这也是引起“噪声”的主要原因。

图2 电刷镀层的瑞利波信号

图3 电刷镀层微观组织

根据图2中瑞利波信号可知，当镀层厚度不同时，瑞利波在其中的传播速度也不同，这就表明瑞利波在电刷镀层中的传播速度可作为镀层厚度无损表征的一个参量，而由于镀层厚度的改变对瑞利波波速的影响较小以及瑞利波信号中存在较多“噪声”信号，因而由镀层厚度改变而引起的信号间时间差的计算精度也就成为保证镀层厚度评价结果的重要因素。式（2）表明，当“噪声”信号较强时，互相关步长n值是影响互相关系数函数计算结果的重要因素，因而本试验分别计算了不同n值时，不同厚度镀层的瑞利波信号与参考信号间的时间差，并建立了镀层厚度-时间差关系曲线，结果如图4所示。为了便于描述，本试验假设瑞利波信号波形符合正弦规律。

图4 电刷镀层厚度-时间差关系曲线

以镀层厚度为零时的瑞利波信号为参考信号，分别计算不同厚度镀层的瑞利波信号与参考信号间的时间差。当互相关系数函数步长n值分别为1/4、1/2、3/4、1、5/4、3/2和7/4周期时，镀层厚度-时间差曲线如图4所示。对比分析可知，随着镀层厚度的增加，瑞利波在镀层中通过相同距离所用的时间逐渐变长，这与图2中瑞利波信号变化规律是相同的，并且随着镀层厚度的增加，由镀层厚度改变而引起的信号间时间差的变化速率逐渐变大。对比不同n值时镀层厚度-时间差曲线可知，当n值较小时，镀层厚度-时间差曲线波动较大，而随着n值的增加，镀层厚度-时间差曲线逐渐趋于平稳；当n值达到1时，再随着n值的增加，镀层厚度-时间差曲线基本重合，并且波动较小。这主要是因为电刷镀层组织中的“孔洞”缺陷引起的“噪声”会使瑞利波波形发生一定程度的“畸变”，而由于互相关函数是在对比波形相似程度的基础上计算信号间时间差的一种方法，因而当n值较小时，波形“畸变”对互相关函数值影响较大，并且互相关函数最大值不明显，即镀层厚度-时间差曲线波动较大；而随着n值的增加，波形“畸变”对互相关系数函数值的影响逐渐变小，即互相关函数曲线逐渐趋于平稳，如图5所示。

图5是镀层厚度为78μm时，不同n值时的互相关函数曲线。对比分析可知，当n值较小时，曲线波动较大，最大值不明显，并且计算结果误差较大；而随着n值的增加，曲线逐渐趋于平缓，并且最大值较明显，这与图4中曲线变化规律是相同的。综合上述分析结果认为，采用互相关系数函计算由于镀层厚度变化而引起的瑞利波信号间时间差时，当n值为1时，即参考函数长度为1个周期时最佳。

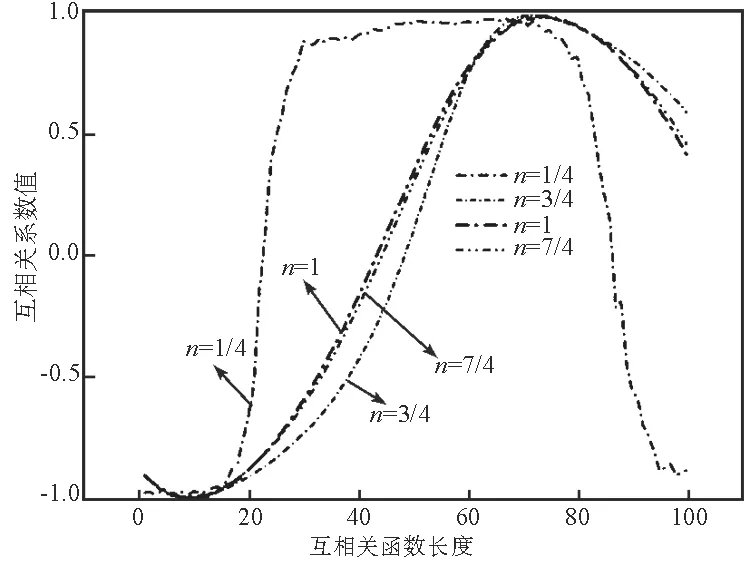
图5 不同n值时互相关系数函数曲线

2.2 结果验证

为了实现电刷镀层厚度的无损评价，结合图4中电刷镀层厚度-时间差关系曲线变化趋势，本试验采用幂函数对计算结果进行拟合，拟合结果如图6所示。

图6 镀层厚度-时间差拟合及验证结果

形式幂函数对电刷镀层厚度-时间差结果拟合得到的结果，可表示为：

图6为采用

式中：

t——瑞利波在电刷镀试样中通过相同距离所用的时间差；

h——电刷镀层厚度。

为了验证采用式（3）对电刷镀层厚度进行评价的可行性，本试验采用相同工艺制备了测量厚度分别为34、42、55和83μm的电刷镀试样，并采用式（2）计算了不同厚度镀层的瑞利波信号与参考信号间的时间差，计算结果分别为36、56、68和192ns，将其带入式（3）得到镀层厚度理论值分别为38.9、47.0、51.2和80.0μm，其相对误差最大值为12.6%，在误差允许范围内。分析可知由于“尖端放电”效应，镀层表面并不平整，因而瑞利波在镀层中传播时，瑞利波通过的实际声程并不完全相同，因而镀层厚度评价结果会有偏差。但相对于镀层厚度而言，镀层平整度对计算结果造成的影响非常小，因而可忽略不计。综合上述分析结果认为采用该方法对电刷镀层厚度进行无损表征是可行的。

3 结论

1）随着电刷镀层厚度的增加，瑞利波在电刷镀层中的传播速度逐渐变小，但其改变速率却逐渐变大；

2）随着互相关函数步长n值的增加，电刷镀层厚度-时间差曲线波形逐渐趋于平稳，当n值达到1时，再随着n值的增加，电刷镀层厚度-时间差曲线基本重合，因而认为n值为1时，参考函数长度最佳；

3）试验结果表明，在互相关函数计算时间差的基础上，采用声程固定不变一发一收模式的双瑞利波探头对电刷镀层厚度进行检测，并通过镀层厚度-时间差的幂函数拟合结果可实现电刷镀层厚度的无损表征。

[1]徐滨士，朱绍华，刘世参，等. 表面工程的理论与技术[M]. 北京： 国防工业出版社，2010.

[2]董允. 现代表面工程技术[M]. 北京： 机械工业出版社，1999.

[3]徐龙堂. 电刷镀镍基含纳米粉复合镀层性能、结构和沉积机理[D]. 北京： 北京工业大学，2000.

[4]张连芳，柯伟平. 超声波波型转换与表面波的检测[J]. 物理试验，2006，26(02)：8-10.

[5]王寅观，田冲，姚国民，等. 利用Rayleigh表面波无损检测热套圆盘的平面残余应力的研究[J]. 声学学报，1999，24(01)：53-58.

[6]吴正毅. 测试技术与测试信号处理[M]. 北京：清华大学出版社，2001.

[7]Fedi M. Localized denoising filtering using the wavelet transform[J]. Pure and Applied Geophysics， 2000，157(09)： 1463-1469.

[8]Perov D V， Rinkevich A B. Wavelet filtering of signals from ultrasonic flaw detector[J]. Russian Journal of Nondestructive Testing， 2002， 38(12)： 869-882.

[9]向阳，彭勇，赵国文. 互相关与应力波波速估计的研究[J]. 无损探伤，2004，28(04)：4-6.

[10]张晓东，高波，宋之平. 互相关函数法在声学测温技术中的应用研究[J]. 中国电机工程学报，2003，23(04)：185-188.

[11]王萍，万柏坤，程烨. 精确的互相关算法在超声波流速测量中的应用[J]. 传感器与微系统， 2007，26(09)：107-112.

[12]苗锦，刘志强，张跟鹏. 基于互相关的时延估计方法及其精度分析[J]. 舰船电子工程，2008(06)：98-100.

[13]蒋斌，徐滨士，董世运，等. 电刷镀纳米颗粒复合镀层的组织与沉积过程[J]. 表面技术，2005，34(03)：16-17.