基于局部屈曲、压损载荷的帽型长桁截面优化设计

刘　卫　何周理 /

(1. 中国商飞北京民用飞机技术研究中心，北京 102209；2. 上海飞机设计研究院，上海 201210)

0　引言

由蒙皮、长桁、框组成的半硬壳式壁板是大型商用飞机常见的结构。帽型长桁的截面尺寸较大，其两边突缘与蒙皮相连形成一个闭合截面，具有很高的受压稳定性[1],是壁板结构中效率较高的纵向加强件。但帽型长桁为封闭结构，内部缺陷不易检查，内腔容易积液而产生腐蚀，因此在金属半硬壳式壁板中，帽型长桁的使用受到了极大的限制。随着比强度高、耐腐蚀性好的碳纤维复合材料大量应用于现代商用飞机上，帽型长桁成为了设计师首选的纵向加强件。

国内外针对金属和复合材料壁板优化已经做了大量研究工作。Kidane等采用了一种典型单元体模型分析格栅加筋筒结构总体屈曲[2]，Jaunky等采用改进的等效法分析了不同类型壁板结构的稳定性，且结合职能算法对复合材料格栅加筋结构的优化问题进行了研究[3]，常楠、张铁亮等对加筋采用两级方法进行优化分析[4-5]，张国柱等通过代理模型进行金属加筋板的布局优化[6]。但在初步尺寸设计[7]时，帽型长桁的截面尺寸对设计师来说显得尤为重要。模型的适当简化是缩短研制时间的重要途径之一，本文通过局部屈曲和压损工程算法来优化帽型截面尺寸，并得出：(1)帽型长桁局部屈曲载荷与帽底宽度，帽腰和帽底夹角的曲线；(2)压损载荷与帽底宽度，帽腰和帽底夹角的曲线，为设计师在初步尺寸设计时提供参考，缩短研发时间。

1　几何模型

选取一段长200 mm的共固化蒙皮、帽型长桁作为研究对象，其截面几何如图1所示。

图1　蒙皮、长桁截面

把帽底宽度W，帽腰和帽底夹角α作为变量，α取值范围为50°～80°，W的取值范围为60 mm～80 mm。

蒙皮铺层为:

[45/0/0/- 45/0/90/90/0/- 45/0/0/45]。

长桁铺层为:

[45/0/- 45/0/90/0/- 45/0/45]。

材料：选取典型的T300碳纤维材料作为研究对象，材料参数见表2。

2　局部屈曲

2.1 局部屈曲计算方法

长桁局部屈曲载荷计算方法采用参考文献[8]5.7.1.3节和5.7.1.5节中介绍的分析方法，分析模型如图2所示。

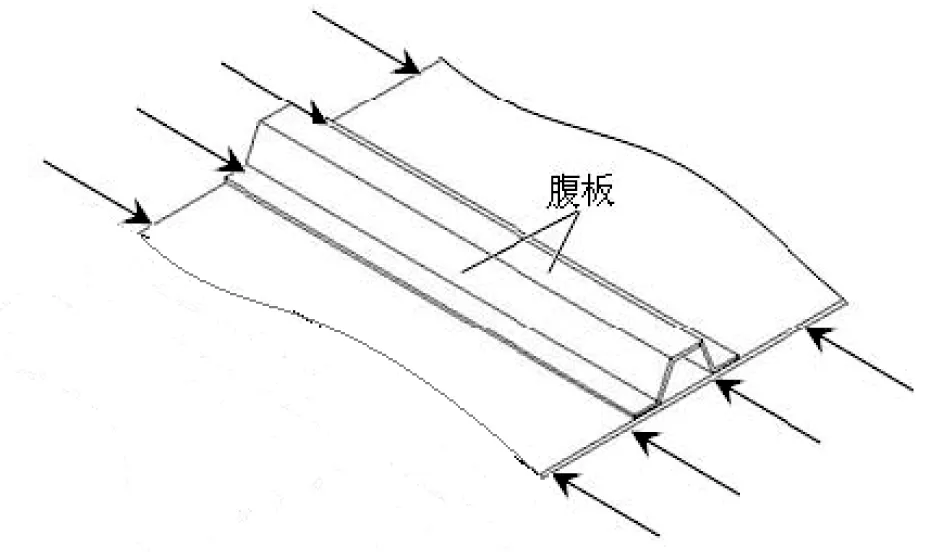
图2　加筋壁板长桁中的腹板

开口薄壁剖面长桁的突缘可作一长边自由，另一长边简支的长板处理，按式(1)计算突缘的轴压局部屈曲载荷。

(1)

式中，Nxcr为单位宽度上的轴压屈曲载荷；bt为突缘的宽度；L为长桁的长度；D11、D66为层压板的纵向弯曲刚度和扭转刚度。

对于薄壁长桁的腹板，可当作两长边简支的长板处理，计算局部屈曲载荷

(2)

式中，bf为腹板的宽度；D12、D22为—层压板的泊松弯曲刚度和横向弯曲刚度。

取突缘和腹板局部屈曲载荷的最小值作为长桁的局部屈曲载荷。

2.2 局部屈曲分析方法

把帽缘条看作突缘，其两边可作一边自由，一边简支处理；把帽腰看作腹板，两边可作简支处理；把中间蒙皮看作腹板，两边可作简支处理，如图3所示。

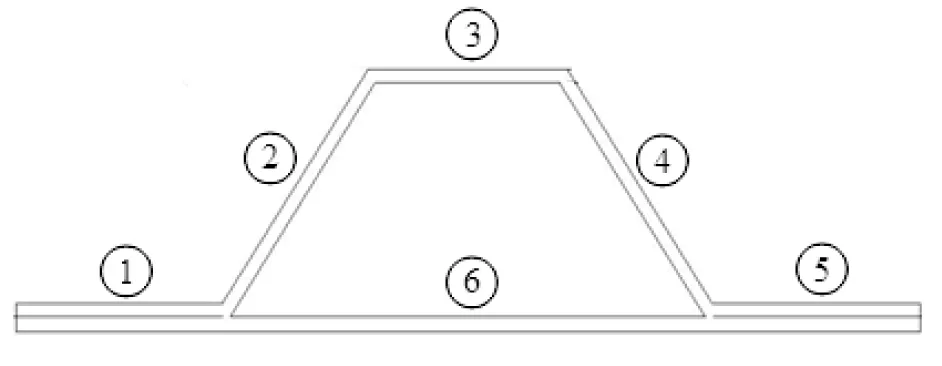
图3　分析所对应的6个单元

2个帽缘条①和⑤，2个帽腰②和④，1个帽顶③，以及帽底中间蒙皮⑥，共6个单元屈曲载荷，将最小值作为长桁的局部屈曲载荷。

各单元的弯、扭刚度如表1所示。

表1　各单元弯、扭刚度

2.3 计算结果

当α=80°时，局部屈曲载荷取得最小值，如图4所示。在这种情况下，局部屈曲载荷随变量W的变化曲线如图4所示，显然，当α=80°，W=80 mm时，局部屈曲载荷取得最小值4 047 N，如图4所示。

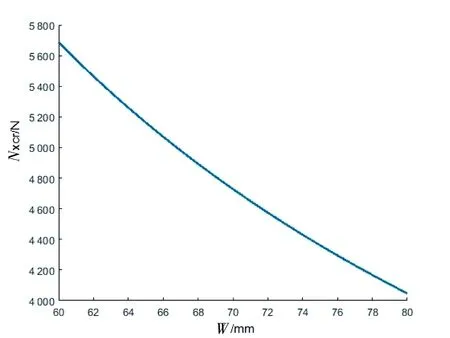
图4　局部屈曲载荷随W的变化曲线

给定α为50°～80°和W为60 mm～80 mm的条件下，计算出局部屈曲载荷随W、α变化如图5所示。

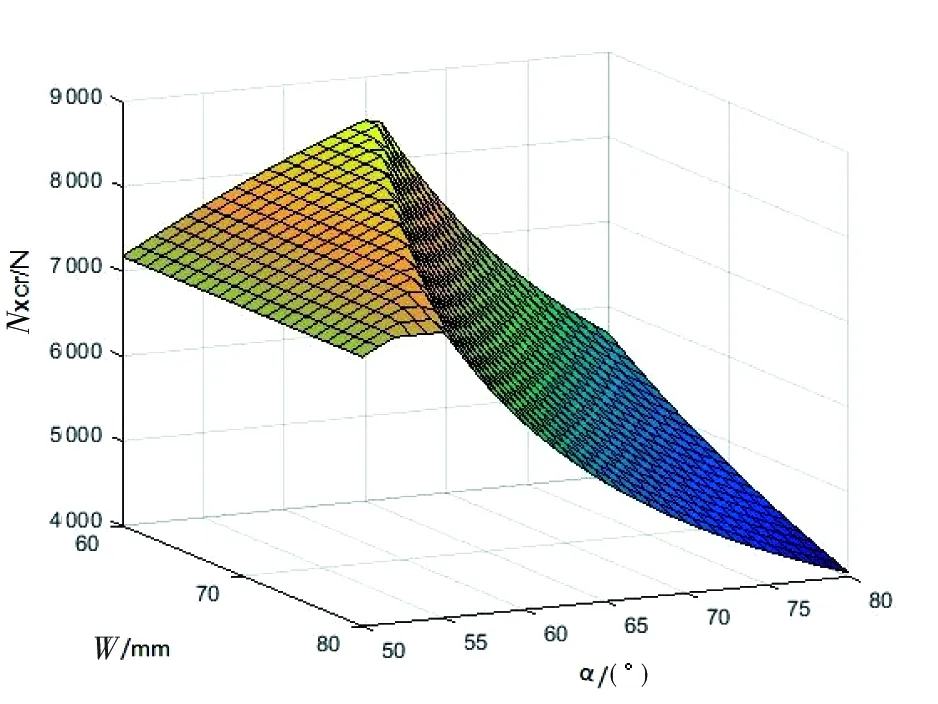
图5　局部屈曲载荷随W,α的变化曲线

3　压损

3.1 压损计算方法

长桁压损载荷计算方法采用参考文献[8]5.7.2.4节中介绍的分析方法，计算方法如下：

(3)

σcu=εcrExc

(4)

(6)

式中，b为腹板或者突缘的宽度；εcr为层压板纤维方向的压缩许用值；Exc为层压板x方向的面内刚度；Eyc为层压板y方向的面内刚度；μxy，μyx为层压板面内等效泊松比。

对长桁的组成单元逐一计算：

对于一边自由、一边简支的组成单元：m=0.575，e=-0.797。

对于没有自由端的组成单元：m=0.868，e=-0.869。

取各组成单元的σcc和σcu中的最低值，求其加权平均值得到压损许用值：

(7)

压损载荷Fcc计算公式为：

(8)

3.2 压损分析

分析2个帽底、2个帽腰、1个帽顶和帽底中间蒙皮共6个组成单元的压损许用值，再进行加权平均得到整个长桁的压损许用值，如图2所示。该帽型长桁的材料力学参数见表2。

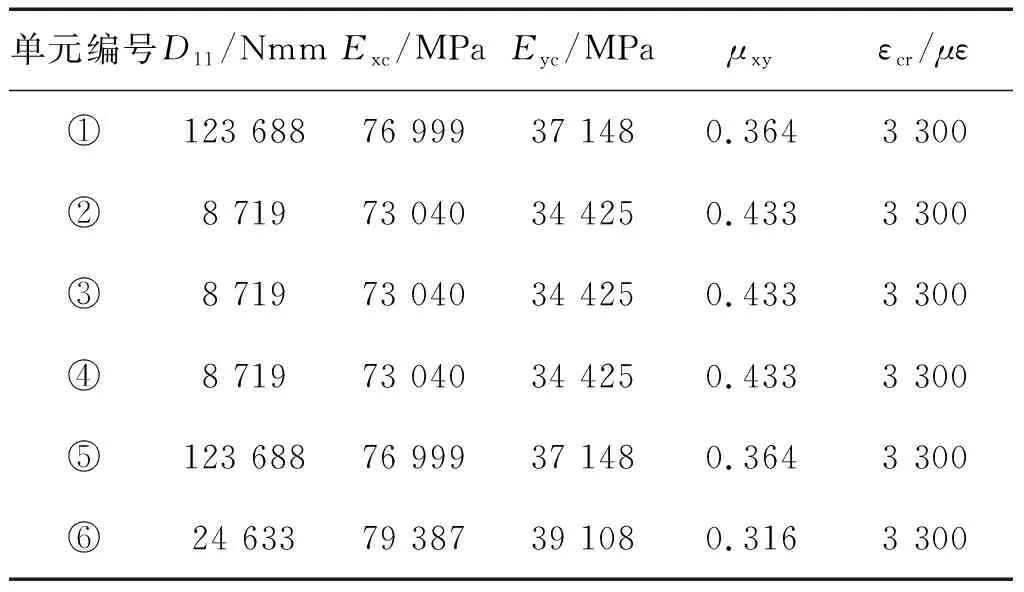
表2　材料力学参数

3.3 计算结果

压损许用值σcc的计算结果如图6所示。当α=50°，w=61.62 mm时，压损许用值取得最大值145.9 MPa；当α=80°,w=80 mm时压损许用值取得最小值120.77 MPa。

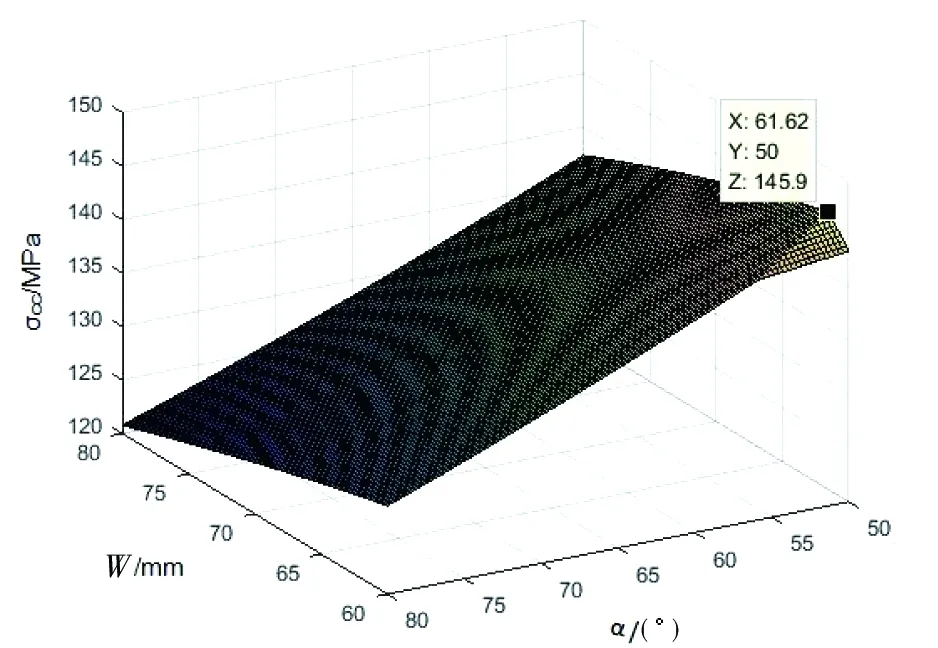
图6　压损许用值随W，α的变化曲线

压损载荷Fcc的计算结果如图7所示。当α=80°，W=80 mm时，压损载荷取得最大值48.69 kN；当α=50°，W=60 mm时，压损载荷取得最小值46.68 kN。

图7　压损载荷随W，α的变化曲线

4　结果对比

给定角度α，局部屈曲载荷和压损许用值的计算结果如图8、图9所示。

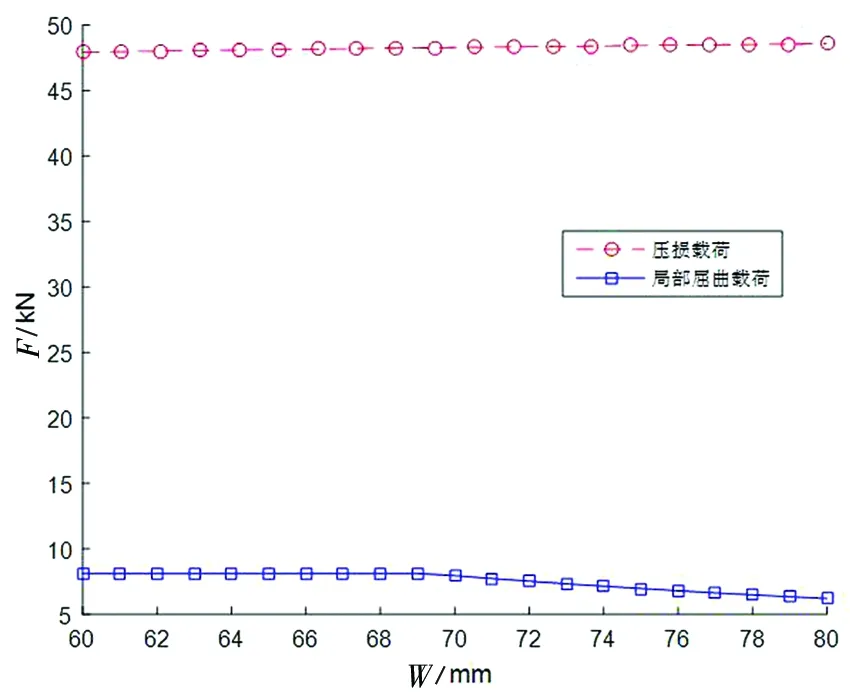
图8　压损、局部屈曲计算结果对比(α=60°)

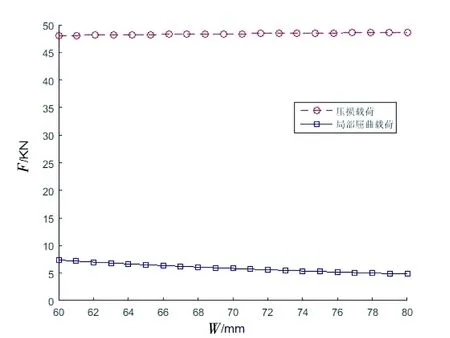
图9　压损、局部屈曲计算结果对比(α=70°)

从图8中可以看出，当α为60°时，影响长桁截面设计的载荷是局部屈曲载荷。局部屈曲载荷在W为60 mm～70 mm的区间内变化微弱，曲线表现为平直；局部屈曲载荷在W为70 mm～80 mm的区间内变化较为明显，曲线有一定的斜率，且随着W的增大，局部屈曲载荷变小。

从图9中可以看出，当α为70°时，影响长桁截面设计的载荷也是局部屈曲载荷。局部屈曲载荷在W为60 mm～80 mm的区间内变化较为明显，曲线有一定的斜率，且随着W的增大，局部屈曲载荷变小。

4　结论

1) 影响帽型长桁截面设计的载荷是局部屈曲载荷；

2) 在局部屈曲状况下，屈曲载荷随帽型长桁底宽的增大而减小；

3) 在局部屈曲状况下，屈曲载荷先随帽腰和帽底的夹角α增大而增大，当α为63°时屈曲载荷为最大，随后α变大屈曲载荷变小；

4) 在压损状况下，压损许用值随帽型长桁底宽、帽腰和帽底的夹角α增大而减小。