基于遗传算法和极限学习机的智能算法在基坑变形预测中的应用
2018-07-10陈艳茹
陈艳茹
(陕西铁路工程职业技术学院, 陕西 渭南 714099)
0 引言
近年来,我国城市建设得到了快速发展,而随之产生的基坑工程数量也越来越多,由于基坑工程会诱发基坑周边环境产生较大变形,因此基坑变形监测及预测成为基坑变形控制的重要内容,受到广泛关注[1-2]。目前,许多学者在基坑变形预测方面进行了深入研究,并取得了相应的成果,渠孟飞等[3]利用支持向量机构建基坑水平位移预测模型,分析了不同工况下的预测效果,结果表明该模型能有效预测基坑变形的发展趋势,预测效果较好; 杨帆等[4]构建了果蝇算法优化的灰色神经网络模型,经实例检验,该模型的预测精度较高,预测值与实测值的一致性较好; 林楠等[5]利用最小二乘法优化支持向量机的核参数,构建了基坑水平位移预测模型,经实例验证,该模型的收敛速度快、预测精度高,对基坑安全监控具有一定的实用价值; 文献[6-9]将神经网络引入到基坑的变形预测或参数反演中,验证了智能神经网络在基坑工程中的适用性。上述研究虽然取得较好的成果,但传统智能神经网络模型的参数设置复杂,且均未涉及极限学习机在基坑变形预测中的应用。极限学习机在其他领域的应用效果较好,如高彩云[10]利用极限学习机构建了滑坡变形预测模型,实测结果表明,该方法较传统神经网络模型具有更高的预测精度; 戴波等[11]结合混沌理论和极限学习机的优点,构建了大坝变形的优化预测模型,有效掌握了大坝变形特征。因此,本文提出利用极限学习机构建基坑变形预测模型,即先利用皮尔逊相关系数评价不同影响因素与基坑沉降变形之间的相关性,再采用试算法确定最优激励函数和隐层节点数,并利用遗传算法确定极限学习机的最优初始权值和阈值,综合构建一种新型优化智能预测模型。本文研究旨在探讨极限学习机在基坑变形预测中的效果,为基坑变形预测研究提供一种新的思路。
1 基本原理
1.1 极限学习机原理
极限学习机(ELM: extreme learning machine)是一种新型的前馈神经网络,为单隐层结构,即网络结构为输入层、隐层和输出层。若基坑变形监测样本为(xi,ti),结合ELM模型的基本原理,可将该模型的标准形式表示如下:
(1)
式中:yj为ELM模型的预测值;L为隐层节点数;βi为第i个隐层节点与输出节点间的连接权值;g(x)为激励函数;wi为输入层与第i个隐层节点间的连接权值;xj为第j个输入样本;bi为各隐层节点的阈值。
通过对权值、阈值的训练,可实现预测误差趋近于0,即:
(2)
式中:N为训练样本数;tj为样本期望值。
结合式(1)—(2),可将ELM模型的标准形式变换为:
(3)
进一步将式(3)表达为矩阵形式,即:
T=H·β。
(4)
式中:T为网络输出矩阵;H为隐层输出矩阵;β为连接权值矩阵。
由于wi和bi可在训练初始给出,加上g(x)无限可微,因此,ELM模型的训练过程可看作求解β矩阵最小二乘解β′的问题,即:
β′=H+·T。
(5)
式中H+为矩阵H的摩尔-彭罗斯广义矩阵。
同时,根据文献[10-12]的研究成果,ELM模型的相关参数设置对预测结果具有一定影响:
1)激励函数类型。ELM模型具有Sigmiod型、Sine型、Hardlim型3种激励函数,各激励函数的泛化能力在不同实例中的预测效果具有差异。
2)隐层节点数。隐层节点数可直接影响网络学习效率,进而影响预测效果。
3)初始权值和阈值的随机性。根据ELM模型的基本原理,在训练或学习过程中,网络权值和阈值是随机产生的,对预测结果的稳定性具有较大影响。
为解决上述问题,本文提出利用试算法确定最优激励函数和隐层节点数。根据传统计算公式,隐层节点数
(6)
式中:m和N分别为输入层和输出层的节点数;a为修正常数,取值区间为[0,10],其值越大,运算量越大,但会提高预测精度,因此为保证预测精度,将a值确定为10。
根据本文预测模型结构,输入层节点数为5,输出层节点数为1,通过式(6)初步确定隐层节点数为12。
首先,将隐层节点数确定为12,对不同激励函数的预测效果进行试算,以确定最优激励函数;然后,对隐层节点数进行试算,试算区间为[9,15],以确定最优隐层节点数。针对初始权值和阈值的随机性问题,提出利用遗传算法对ELM模型初始权值和阈值进行优化,以增强预测模型的全局优化能力,具体优化过程见文献[12]。
1.2 皮尔逊相关系数
基坑变形影响因素较多,为分析不同影响因素与变形值之间的相关性,提出利用皮尔逊相关系数衡量两变量间的相关性程度[13-14]。若将两评价序列的数据记为(Xi,Yi),则皮尔逊相关系数的计算公式为:
(7)
式中:r为皮尔逊相关系数;Xi、Yi分别表示两变量第i个节点处的值;X′、Y′分别为两检验变量的均值;n为序列长度。
相关系数r的取值区间为[0,1],即|r|≤1。r值为正时,说明两序列呈正相关,即两者的发展趋势相同;r值为负时,说明两序列呈负相关,即两者的发展趋势相反; |r|值越大,说明两变量序列的相关性越高,反之相关性越低。根据相关系数r的大小,对两评价序列的相关性程度进行划分,共划分为3个区间,如表1所示。

表1 相关性程度区间划分明细
1.3 预测思路
根据上述基本原理,本文模型的预测步骤如下:
1) 利用皮尔逊相关系数评价不同基坑变形影响因素与基坑变形间的相关性程度。
2) 根据影响因素对基坑变形的影响程度,确定极限学习机的输入层指标,并根据试算法确定最优激励函数和隐层节点数。
3) 对不同施工阶段的监测样本进行预测分析,以验证预测模型的有效性和可靠性。
2 实例分析
2.1 工程概况
上海古北财富中心大楼基坑[15]为建筑基坑,拟建综合性商业办公大楼,主要包括1栋35层甲级办公楼、1栋26层酒店及商业裙房等,建筑总面积为117 220 m2,其中工程用地面积为17 997 m2。该基坑共包含4层地下车库,开挖深度较大,最大开挖深度为20.45 m,且近接条件较为复杂: 基坑四周均近接市政公路,路下管线复杂;东北侧近接砖混住宅,采用浅基础天然地基,最小距离为10.6 m; 北侧近接一栋历史保护建筑——原宋氏住宅,该建筑为砖木结构,基础抗变形能力较差。
该基坑场地属滨海平原地貌,覆盖层以软黏土为主,厚度达80 m,基坑深度范围内涉及8个土层,各层具有若干亚层,具体参数见表2。

表2 土层参数统计
综合考虑基坑所处地质条件,确定围护结构采用地下连续墙+4道水平支撑的形式。根据开挖阶段的不同,将基坑开挖过程分为5个阶段: 第1阶段开挖至深度1.55 m,并设置第1道支撑; 第2阶段开挖至深度6.85 m,并设置第2道支撑; 第3阶段开挖至深度11.85 m,并设置第3道支撑; 第4阶段开挖至深度16.05 m,并设置第4道支撑; 第5阶段开挖至基坑坑底设计标高。
由于基坑所处区域为深厚软土地区,基坑沉降变形明显,对基坑结构稳定性的影响较大,因此,在施工过程中,对基坑的沉降变形进行重点监测,共计布设93个监测点,其中F81监测点的沉降变形数据如图1所示,监测频率为2 d/次。结合开挖过程和监测时间,将监测数据划分为5个工况,且各工况与开挖阶段对应,其中第1工况对应第1~21周期、第2工况对应第22~36周期、第3工况对应第37~48周期、第4工况对应第49~58周期、第5工况对应第59~79周期。
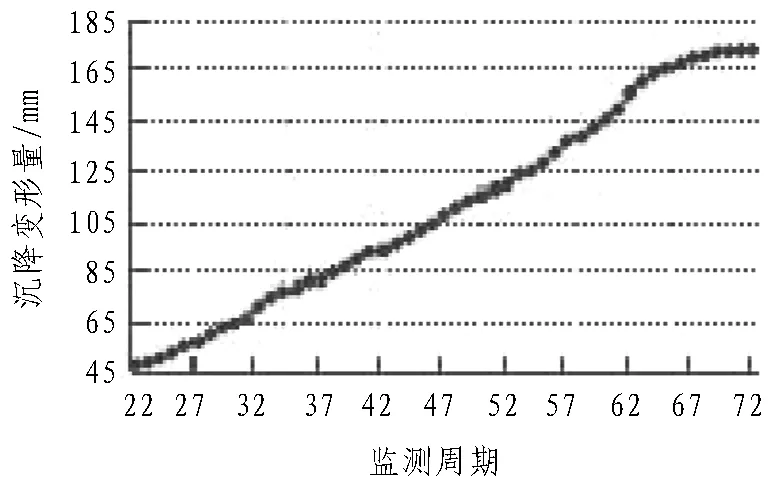
图1 F81监测点的沉降变形曲线
为进一步分析基坑变形特征,对基坑沉降变形速率进行统计,其沉降速率曲线如图2所示。由图2可知,基坑沉降速率的波动性较大,但均为正值,说明基坑变形受施工扰动影响较大,且具有持续增长的特征,其中最大变形速率为3.00 mm/d,最小变形速率为0.05 mm/d,平均变形速率为1.22 mm/d。

图2 F81监测点的沉降速率变形曲线
为了解基坑变形速率的分布特征,结合最大变形速率,将基坑沉降速率量值范围等分为3个区间,分布情况见表3。由表3可知,基坑沉降速率量值多分布在第2区间,所占比例为60.78%,其次是第1区间和第3区间,所占比例分别为29.41%和9.80%,说明基坑沉降速率分布区间相对集中。

表3 沉降速率区间分布统计
2.2 相关性分析
据文献[15]的研究成果,开挖时间、开挖深度、土体抗剪参数及重度等因素对沉降变形影响较大。为充分分析各影响因素对基坑变形的影响程度,基于不同施工工况,以皮尔逊相关系数为评价指标,分析开挖时间、开挖深度、土体抗剪参数及重度与沉降变形之间的相关性。鉴于第1工况开挖深度较浅,且多为杂填土,土体性质不具有代表性,使得该工况的监测数据规律性弱,因此本文不对第1工况进行研究,其余工况下的相关系数计算结果统计见表4。
由表4可知,在不同工况下,各参数与沉降变形值之间的相关系数均具有差异,说明各参数对基坑沉降变形的影响具有阶段性。其中,4种工况条件下,开挖时间、开挖深度与沉降变形间的相关系数均趋近于1,且均为正值,说明两参数对基坑沉降变形的影响呈正相关,且为高度相关; 在第2、3工况条件下,土体重度及抗剪强度与沉降变形间的相关系数均为负值,呈显著负相关,但在第4、5工况条件下,土体重度及抗剪强度与沉降变形间的相关系数均为正值,呈显著正相关,说明土体重度及抗剪强度的3个参数对基坑沉降变形的影响具有一致性,且在较大程度上影响了基坑的沉降变形。综上所述,开挖时间、开挖深度、土体抗剪强度及重度均与基坑沉降变形显著相关,但在影响程度上具有差异。
表4不同工况下参数的相关系数计算结果统计
Table 4Statistics of correlation parameters under different conditions
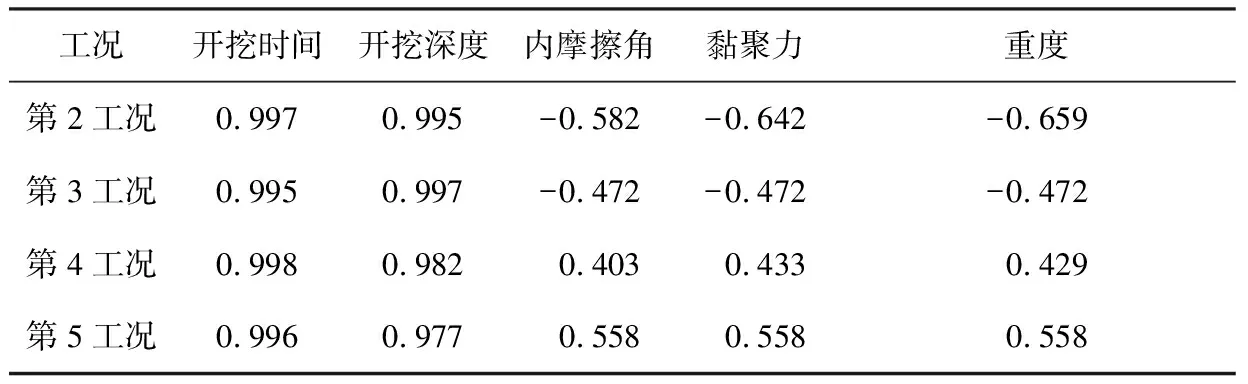
工况开挖时间开挖深度内摩擦角黏聚力重度第2工况0.9970.995-0.582-0.642-0.659第3工况0.9950.997-0.472-0.472-0.472第4工况0.9980.9820.4030.4330.429第5工况0.9960.9770.5580.5580.558
2.3 预测分析
根据2.2节分析可知,开挖时间、开挖深度、土体抗剪强度及重度与基坑沉降变形相关。因此,结合ELM模型的基本原理,将上述5个指标作为输入指标,将对应时间节点处的变形值作为输出指标。同时,主要以第2工况监测样本作为训练样本,第3、4、5工况作为验证样本,且限于篇幅,仅列出后3个工况最后6个周期的预测结果,即第3工况的验证周期为第43~48 周期,第4工况的验证周期为第53~58周期,第5工况的验证周期为第67~72周期。
结合文章思路,利用第3工况来确定最优激励函数、隐层节点数、初始权值和阈值。首先,将隐层节点数设置为12,以计算不同激励函数的预测效果,结果见表5。对比不同激励函数的预测结果,得出3种激励函数的预测效果存在一定差异,以Sigmiod型激励函数的预测效果最优,其次是Hardlim型和Sine型激励函数。因此,确定ELM模型的激励函数为Sigmiod型激励涵数。
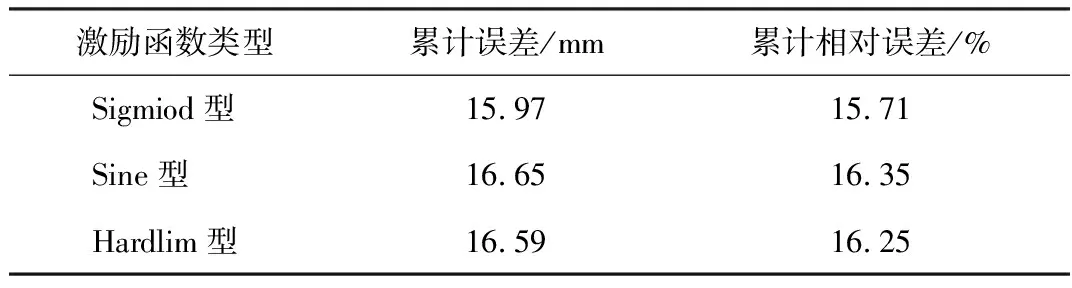
表5 不同激励函数的预测结果
其次,对区间[9,15]的隐层节点数的预测结果进行试算,以确定最优隐层节点数,结果见表6和表7。由表6和表7可知,不同隐层节点数对预测结果的影响较为明显,其中最优隐层节点数为13,其累计相对误差为13.95%;而最差隐层节点数为9,其累计相对误差为19.23%,两者相差5.28%,说明隐层节点数对预测结果的影响较大,验证了通过试算确定最优隐层节点数的必要性和可行性; 且各验证周期预测结果的相对误差均小于3%,最小相对误差仅为1.51%。因此,确定隐层节点数为13。

表6 不同隐层节点数的预测结果

表7 最优隐层节点数预测结果
最后,利用遗传算法优化ELM模型的初始权值和阈值,构建GA-ELM预测模型,且GA种群大小为60,代沟为0.90,变异概率为0.002,交叉概率为0.65,最大遗传代数为250。通过预测,得到ELM模型优化前后的预测结果,见表8。对比相应监测周期处的预测结果,得出优化后预测结果的相对误差均小于优化前预测结果的相对误差,说明GA-ELM模型的预测效果相对更优; 且在GA-ELM模型的预测结果中,相对误差均小于2%,其中最大、最小相对误差分别为1.65%和0.76%,说明该模型具有较高的预测精度,也验证了遗传算法的优化效果及能力。
表8ELM模型优化前后预测结果对比
Table 8Comparison of prediction results before and after optimization of ELM model
2.4 可靠性验证
根据2.3节研究结果,确定了最优激励函数和隐层节点数,并验证了GA-ELM模型的预测效果,为进一步验证该预测模型的可靠性,再以第4、5工况数据作为可靠性验证样本进行预测,且验证周期分别为第53~58周期和第67~72周期。在验证过程中,将验证周期前的所有监测数据均作为训练样本,实现训练样本的更新和增加,以验证该模型的滚动预测能力。第4、5工况的预测结果见表9。
由表9可知,第4、5工况各验证周期预测结果的相对误差均小于2%。在第4工况的预测结果中,最大相对误差为1.25%,最小相对误差为0.74%; 在第5工况的预测结果中,最大相对误差为1.55%,最小相对误差为0.92%,得出两工况的预测精度均较高,验证了该模型的可靠性,说明该模型具有较好滚动预测能力。
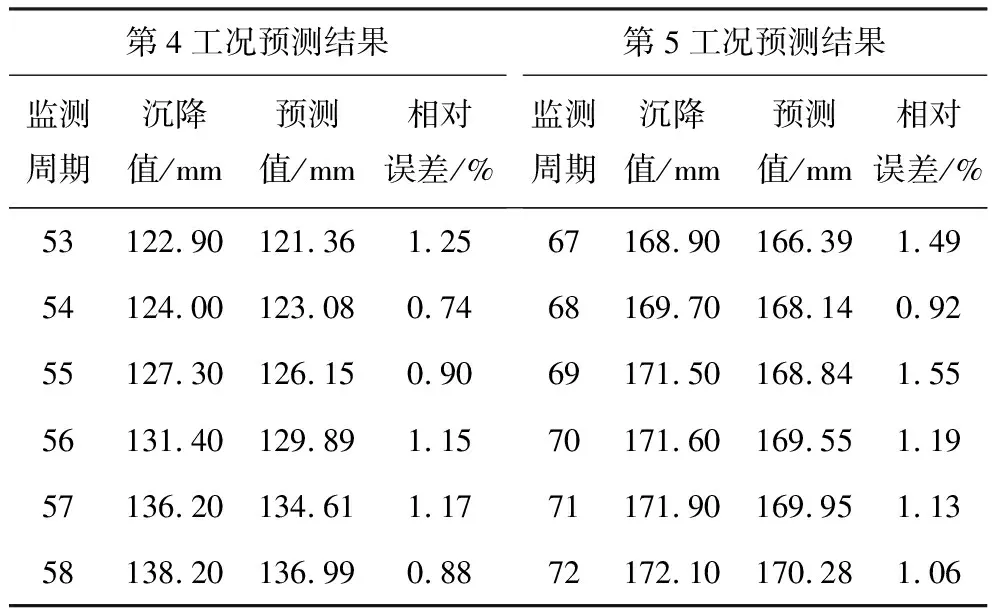
表9 可靠性验证的预测结果
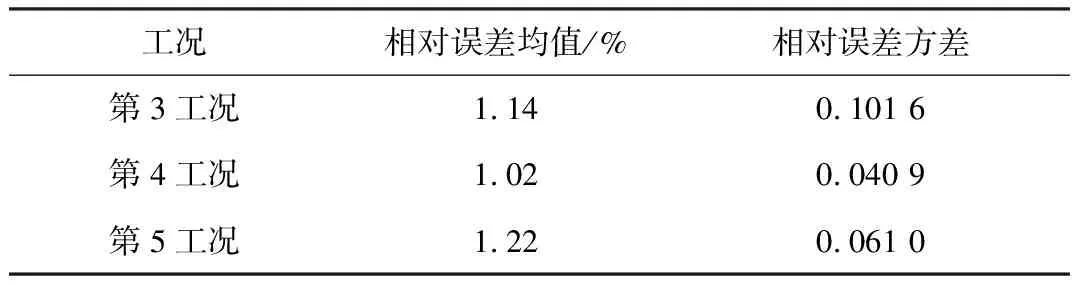
为对比不同工况下的预测效果,将各工况预测结果的相对误差作为评价对象,求解其均值和方差,以评价预测精度及其稳定性,结果见表10。由表10可知,不同工况的预测结果具有一定的差异: 在预测精度方面,第4工况的预测精度最高,其次是第3工况和第5工况; 在预测结果稳定性方面,第4工况的稳定性最高,其次是第5工况和第3工况。
表10不同工况预测结果对比
Table 10Comparison of prediction results under different working conditions
工况相对误差均值/%相对误差方差第3工况1.140.101 6第4工况1.020.040 9第5工况1.220.061 0
综上所述,不同工况的预测效果虽然具有一定的差异,但均具有较高的预测精度,能满足工程需要,验证了该模型的有效性和可靠性。
3 结论与讨论
通过ELM模型在基坑沉降变形中的预测研究,得出如下结论。
1)基坑沉降变形的影响因素较多,通过皮尔逊相关系数能有效评价各影响因素与基坑变形间的相关性,为后期构建变形预测模型提供了一定的指导和依据。
2)ELM模型的参数设置虽然不复杂,但其预测效果很大程度上受激励函数和隐层节点数的影响,且通过试算法确定最优激励函数和隐层节点数能有效提高预测精度,说明该方法具有可行性和必要性。
3)通过优化遗传算法的初始权值和阈值,进一步提高了预测精度,说明GA-ELM模型较ELM模型具有更高的预测能力,适用性更强。
4)不同工况的预测结果均具有较高的预测精度,说明该预测模型具有较高的稳定性和可靠性,也验证了该模型在基坑变形预测中的可行性。
5)鉴于基坑工程区域地质环境及施工手段具有差异性,其变形机制也具有差异,该预测模型在不同地质条件下的预测效果仍需进一步研究。
