基于混沌递进预测模型与趋势检验的深基坑变形规律研究

马　琳

(杨凌职业技术学院建筑工程分院， 陕西 咸阳　712100)

0　引言

随着城市建设的不断发展，基坑的应用越来越多。在基坑的开挖过程中，受基坑深度、规模及近接条件等因素的影响，基坑不可避免会产生变形，且当变形量过大时，会影响基坑自身及其周边建筑物的安全。通过预测基坑变形能有效掌握基坑的变形规律，以便及时采取必要的补救措施，故对其研究具有重要的意义[1-3]。基坑的变形影响因素较多，传统数学方法难以描述其变化关系，需对其预测方法进行深入研究。BP神经网络具有较好的泛化能力、非线性预测能力，较适用于基坑的变形预测，且相关学者已将其应用到基坑的变形预测中。贺永俊等[4]将主成分分析法和BP神经网络进行结合，构建了基坑支护方案的优选模型，实例验证了该模型具有较好的可靠性；胡启晨等[5]和赵健赟等[6]利用BP神经网络构建了基坑的变形预测模型，其预测值与实测值的一致性较好，具有较高的预测精度。上述研究很好地验证了BP神经网络在基坑变形预测中的适用性和有效性，但传统BP神经网络易陷入局部最优解，而遗传算法能有效实现全局寻优，可利用遗传算法GA(genetic algorithm)优化BP神经网络，构建GA-BP神经网络模型。李彦杰等[7]利用遗传算法对BP神经网络的阈值和权值进行优化，构建了GA-BP神经网络模型，经实例验证，该模型具有误差小及预测精度高等优点。通过上述优化，虽然提高了预测模型的全局优化能力，但缺少对预测残差的分析，有必要对预测模型的残差序列进一步优化预测。考虑到残差序列具有明显的混沌特征[8]，再利用混沌理论对残差序列进行分析预测，以提高预测精度。同时，考虑到单一方法分析结果的稳定性及准确性存在一定的不足，再将SR检验法引入到基坑变形趋势的判断中，以验证变形预测结果的准确性。

1　基本原理

为提高变形预测精度，本文提出以BP神经网络为基础，采用遗传算法及混沌理论对预测结果进行递进优化预测，构建了混沌递进预测模型，以期为基坑变形预测提供一种切实有效的方法，预测模型及趋势模型的基本原理分述如下。

1.1　BP神经网络

BP神经网络是一种反向递推修正权值的多层前馈神经网络，具有较强的容错能力、泛化能力及映射能力，一般具有输入层、隐层及输出层3层网络结构[9]，其学习过程包含了正向传播和反向传播2个过程。

1)正向传播过程。该过程是样本由输入层传入，并经隐层传至输出层，若输出结果能满足期望误差，则终止训练，输出结果；若输出结果不能满足期望误差，则进入反向传播阶段。

2)反向传播过程。该过程是将输出结果经隐层向输入层进行逐层反传，并根据预测误差逐步修正各神经元的权值，且当误差分摊完成以后，再进入正向传播过程。

通过正向传播和反向传播的反复循环，逐步修正输出结果的误差值，直到满足期望目标。

在BP神经网络的应用过程中，需对其参数进行合理设置，主要参数设计如下。

1)各层节点数。本文采用的神经网络结构为递推型结构，即以预测节点前的若干节点为输入层，该预测节点为输出层。结合实例，将输入层节点数确定为6，输出层节点数确定为1，根据文献[10]提出的隐层节点

(1)

式中：M为输入层节点数；N为输出层节点数；A为修正常数(取值为0～10，取值越大，预测精度越高，但会增加运算次数)。

为保证预测精度，A值取10，并结合输入和输出层的节点数，确定隐层节点数为13。

2)函数设定。BP神经网络具有多种函数形式，结合工程实际，将输入层与隐层间的传递函数设置为purelin函数，隐层与输出层间的传递函数设置为tansig正切S型函数，训练函数设定为train函数，仿真函数设定为sim函数。

3)学习率。学习率对预测精度及收敛速度具有较大影响，其取值为0.01～0.8，本文采用较小的学习率来保证预测精度，故将学习率设置为0.01。

4)其他参数的设定。为防止运算过程陷入死循环，故将最大迭代次数设置为1 500次。

1.2　遗传算法的优化

为克服BP神经网络易陷入局部最优值的缺点，采用遗传算法优化BP神经网络的初始权值和阈值，以期提高预测精度，并将优化过程[11]分述如下。

1)将BP神经网络的权值向量Wi看做染色体，其个数P作为种群规模数，并将染色体的对应权值和阈值代入神经网络中，得到遗传算法优化过程中的训练误差ΔEi，再通过引入大数M，确定染色体的适应值

F(i)=M/ΔEi。

(2)

2)根据各染色体的适应值，确定选择概率

(3)

3)通过交叉操作，产生新的个体，即

(4)

式中：b为0～1的随机数；P1和P2为随机选择的基因。

4)将2条染色体上的基因进行变异操作，以改变染色体的原始信息，对最优信息进行搜寻。

5)重复上述第2—4步，直到训练结果满足期望误差，对应的权值和阈值即为遗传算法优化得到的最优权值和阈值。

通过将最优权值和阈值代入神经网络中，即可实现遗传算法对BP神经网络的优化预测，且预测值与实测值之间的差值即为残差序列。

1.3　混沌理论的残差优化

残差序列的规律性较弱，具有较强的混沌特征，故采用混沌理论对残差序列进行相空间重构，以实现残差序列的优化预测，对混沌理论的残差优化过程[8]分述如下。

1)相空间重构。若将残差序列表示为{ε1,ε2,…,εn}，根据嵌入维m和延迟时间τ，可将残差序列的m维相空间表述为

ψi=[εi,εi+τ,…,εi+(m-1)τ]T。

(5)

式中ψi为相空间中的第i个相点。

2)求解嵌入维数。在嵌入维数m的求解过程中，先假定初始值m0，并计算其对应的关联维数

(6)

式中：N=n-(m-1)τ，表示残差序列相空间的相点个数；H(*)为Heaviside函数；λ为给定常数。

当λ在一定范围内时，可以通过关联维数和λ之间的对数线性关系确定维数

(7)

一定范围内，d(m)值随m值的增大而逐步增大，当d(m)值不随m值的增大而变化时，对应的m值即为嵌入维数。

3)求解延迟时间τ。根据去偏复自相关法，可确定延迟时间的相关函数

(8)

式中ε′为残差序列长度。

根据C(τ)-τ曲线，C(τ)值随τ值的减小而减小，当C(τ)值减小到1-1/e时对应的τ值即为延迟时间。

4)残差序列的预测。本文采用混沌理论局域法中的Lyapunov指数法进行预测，该方法的预测过程如下。

以ψi为预测中心，并假设其最近相邻点为ψl，则两相点间的距离

(9)

当d值取最小时，预测模型的表达式为

(10)

式中λmax为Lyapunov指数的最大值。

根据上式，通过ψl即可推导出εi+1，实现残差序列的优化预测。

1.4　SR检验

SR检验是一种非参数检验，能有效判断评价序列的变形趋势[12]。在SR检验过程中，其统计量D和检验统计量ZSR的计算公式如下。

(11)

(12)

式(11)和式(12)中：Ri为评价序列中第i个监测值对应的秩；k为评价序列长度。

在变形序列的趋势判断中，若ZSR>0时，评价序列将呈增长趋势，说明基坑变形将趋于增加；反之，评价序列将呈减小趋势，说明基坑变形将趋于减小。同时，当ZSR的绝对值大于t(n-2,1-a/2)时，说明该评价序列的变形趋势性大于水平a时的显著性，且水平a不同，对应的显著性也具有差异，故对不同水平a的显著性进行划分，结果如表1所示。

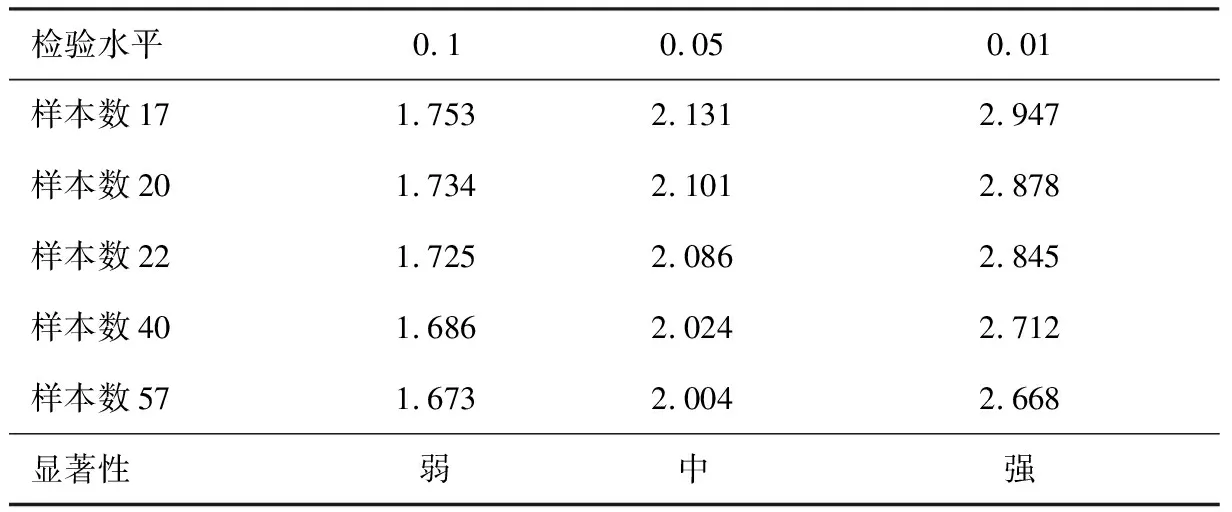
表1　不同水平a的显著性划分

2　实例分析

2.1　工程概况

某基坑[13]为建筑基坑，上部建筑物为办公综合楼，共计有24层。基坑形状为多边形，长度为47～87 m，呈东西向；宽度约60 m，呈南北向。基坑开挖深度为7.95～8.95 m，属深基坑，围护结构采用工法桩。其中，水泥土搅拌桩的桩径为850 mm，内插H型钢，尺寸为H600 mm×300 mm×12 mm×20 mm，中心距为1.2 m，有效长度为16.3 m。

基坑周边地势平坦，属滨海平原地貌，标高区间为3.91～4.95 m，区间内土层主要为杂填土、粉质黏土及粉砂等。土层基本特征参数如表2所示。

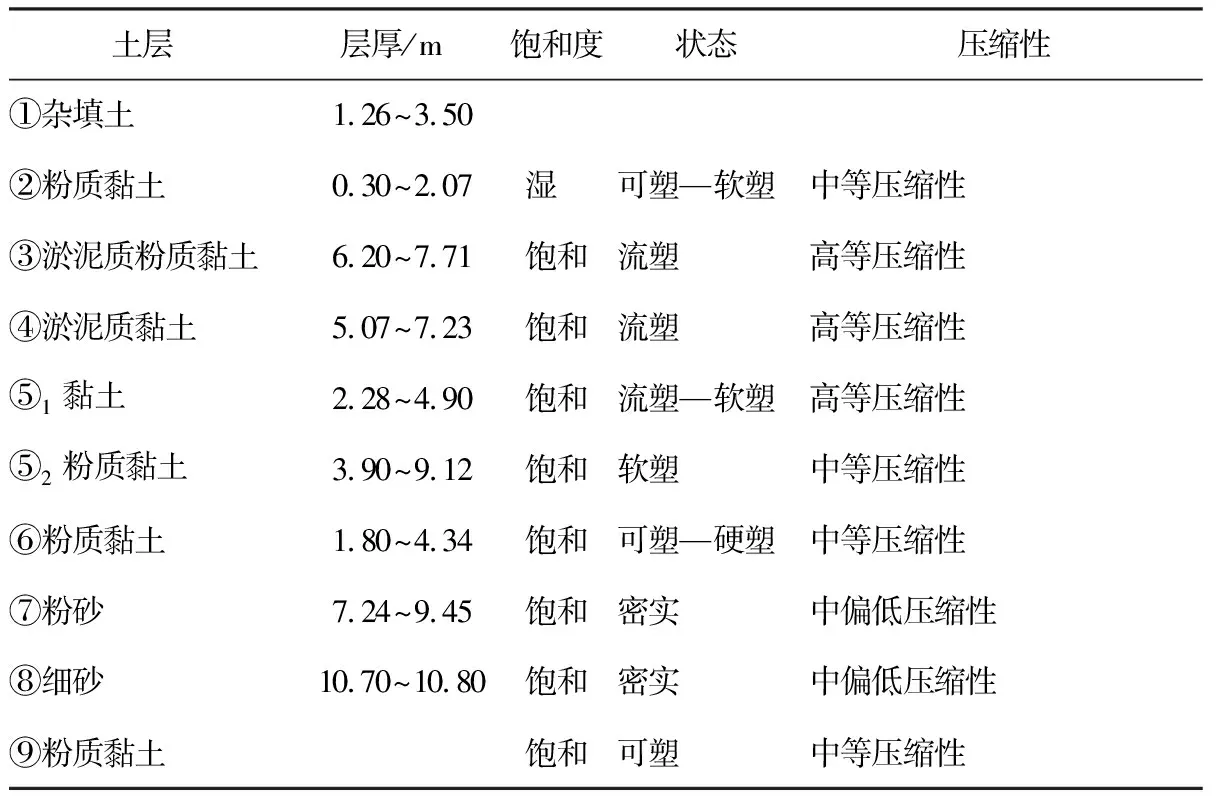
表2　土层特征参数统计

工程涉及范围内的地下水为潜水，水位埋深为0.9～1.2 m。

为及时掌握基坑的变形规律，评价其安全性，对基坑变形进行了监测。其中，D5监测点为基坑周边地表沉降监测点，其沉降数据较为完整，将其作为本文分析的数据来源。D5监测点沉降曲线如图1所示。

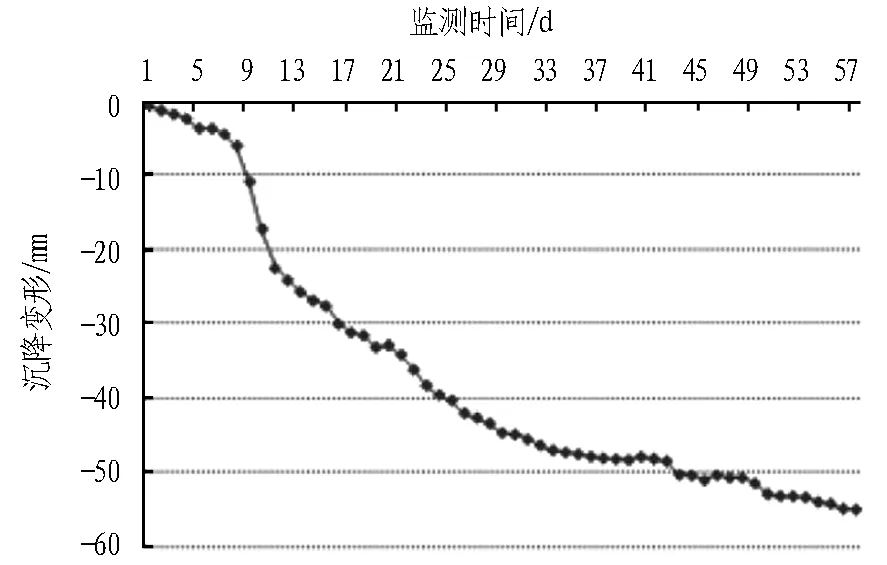
图1　D5监测点的沉降曲线

2.2　变形预测

基坑变形具有持续性，监测样本也会随监测时间的持续而增加。为验证本文预测模型在不同样本量条件下的适用性和有效性，将本文监测周期划分为前期、中期和后期3个阶段，其中，前期样本为1～20周期，中期样本为1～40周期，后期样本为1～57周期，且在预测过程中，均以各阶段的后6个周期为验证周期。

为验证本文模型在递进预测过程中遗传算法及混沌理论的优化效果，以前期为例，对优化过程的预测效果进行详述，得遗传算法优化前后的结果如表3所示。对比优化前后相应节点的相对误差，得出遗传算法能有效提高预测精度，验证了遗传算法的优化效果。在前期GA-BP神经网络的预测结果中，最大相对误差为3.37%，最小相对误差为2.99%，得出相对误差的变化区间相对较小，说明该预测模型的稳定性较好。

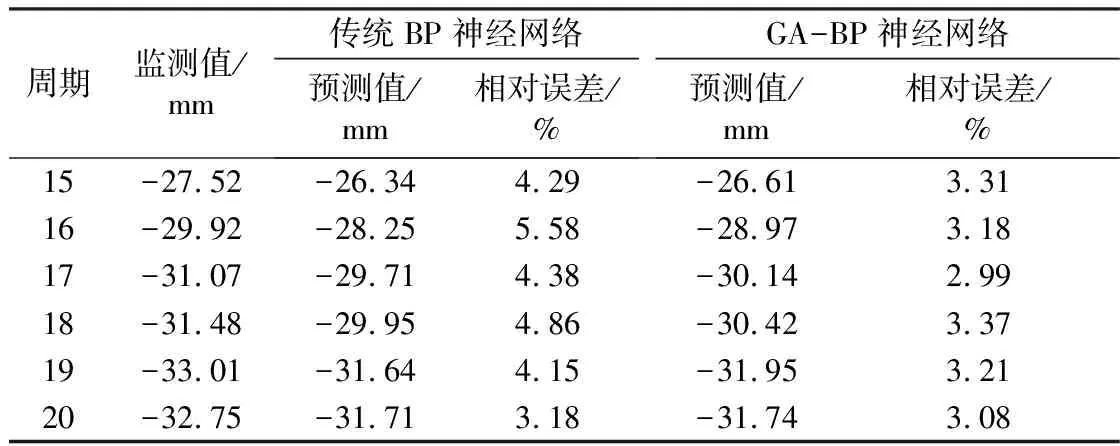
表3　前期遗传算法的优化结果统计

根据递进预测思路，再利用混沌理论对残差序列进行优化预测，结果如表4所示。对比表3和表4可知： 1)混沌理论的残差序列优化效果较好，能有效提高预测精度； 2)经残差优化，预测结果的最大和最小相对误差分别为2.27%和1.13%，平均相对误差为1.89%，预测效果较好。

表4　前期遗传算法的优化结果统计

通过上述前期预测效果的分析，得出遗传算法和混沌理论的递进优化预测效果较好，能有效提高预测精度。再利用本文递进预测模型对中期和后期变形进行预测，结果如表5所示。可以看出： 1)本文预测模型在中期和后期预测结果中的最大相对误差为1.74%和2.31%，平均相对误差为1.38%和1.76%，预测效果均较好，验证了本文预测模型的有效性，也说明该模型的适用性较好，且随样本数的增加，仍能保持较好的预测效果； 2)对58～61周期进行外推预测，得出基坑的沉降变形将会持续增加，但增加幅度偏小。

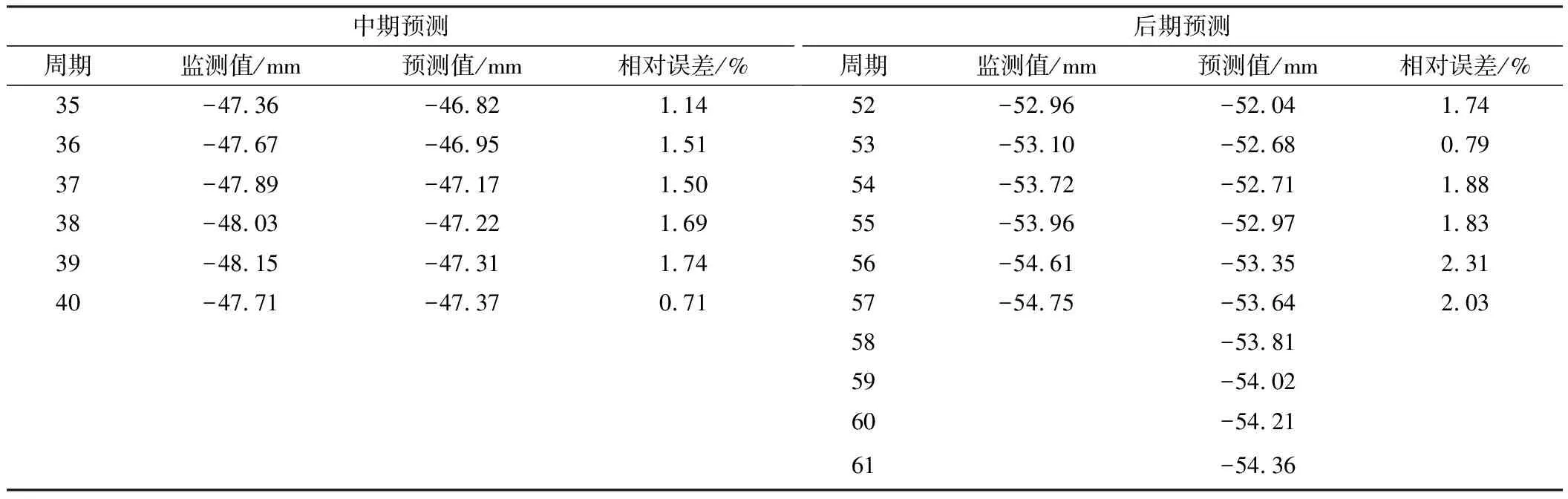
表5　中期和后期预测结果统计

2.3　变形趋势检验

为验证本文递进预测模型的准确性，进一步利用SR检验对基坑的变形趋势进行判断，且结合文献[14]的研究成果(分阶段的趋势分析包含等时段分析和递增时段分析)，本文采用等时段和递增时段2种方式进行分析，结果如表6和表7所示。

表6　等时段趋势分析

表7　递增时段趋势分析

对比表6和表7可知： 对应阶段的趋势性及显著性判断均一致，但中期和后期的ZSR值具有差异，说明分析方式不同时，中期和后期的趋势性及显著性存在相对差异，且以递增时段分析的趋势性及显著性相对更差。

鉴于分析方式不同时，分析结果具有一定的差异，本文提出以2种方式的均值作为基坑分阶段趋势分析的结果，如表8所示。可以看出： 1)3个阶段的基坑变形均呈上升趋势，但对比3个阶段的显著性，得出前期的趋势性最强，中期次之，后期最弱； 2)基坑的后期变形呈上升趋势，但显著性为弱，说明基坑的沉降变形会持续增加，但增加幅度较小，与预测模型的外推预测结果一致，验证了本文递进预测模型的有效性。

表8基坑变形趋势判断结果

Table 8Gudgment results of deformation tendency of foundation pit

阶段ZSR值趋势性判断显著性判断前期3.032 上升趋势强中期2.188 上升趋势中后期1.970 上升趋势弱

2.4　可靠性验证

为验证本文预测模型及趋势分析模型的可靠性，再引入可靠性检验实例进行验证。某基坑[15]为住宅基坑，在施工过程中，进行了系统全面的监测，基坑边缘水平位移监测点共布设19个监测点。S8监测点的变形曲线如图2所示。

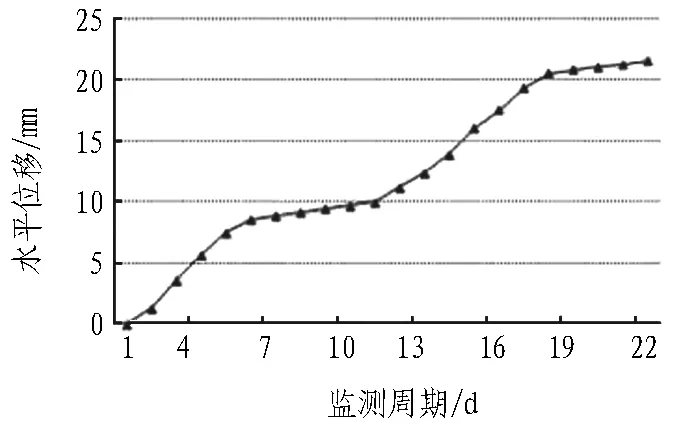
图2　S8监测点的水平位移曲线

2.4.1变形预测

基于本文递进预测模型，对验证实例的水平位移进行预测，结果如表9所示。可以看出： 1)对比各递进阶段相应节点处的相对误差，得出通过逐步递进优化，相对误差值逐步变小，说明通过递进预测能有效提高预测精度，验证了遗传算法和混沌理论的优化能力； 2)最终预测结果的最大相对误差为2.82%，平均相对误差为2.08%，具有较好的预测效果，进一步验证了本文预测模型的可靠性； 3)根据外推预测，基坑的水平位移仍将持续增加，且增长幅度平均为0.37 mm/d，增长速率相对较大。

表9　验证实例的变形预测结果

2.4.2变形趋势分析

利用SR检验对验证实例的变形趋势进行分析，结果如表10所示。可以看出：ZSR值为2.187，得出验证实例的水平变形呈上升趋势，且显著性强，说明验证实例的水平位移仍将持续增加，且增加幅度相对较大，与预测结果一致。

表10　验证实例的变形趋势结果

由上述分析可知： 递进预测模型及SR检验在验证实例中仍有较好的适用性，能对基坑水平位移进行有效预测及趋势判断，验证了预测模型及趋势检验方法的有效性和可靠性。

3　结论与讨论

1)本文以遗传算法、混沌理论、BP神经网络及SR检验为理论基础，构建了基坑的变形预测及趋势判断模型，为基坑的变形规律研究提供了一种新的思路。

2)遗传算法可以很好地实现全局寻优，能有效确定BP神经网络的最优权值和阈值，对提高预测精度具有重要作用。

3)基坑变形预测的残差序列具有明显的混沌特征，通过考虑混沌效应的残差序列优化能有效减小预测误差，验证了混沌优化模型的合理性。

4)SR检验能有效判断基坑的变形趋势，且能对变形的显著性进行合理判断，验证了该方法在基坑变形规律研究中的可行性和适用性。

5)限于篇幅，本文仅验证了递进预测思路在基坑变形预测中的适用性和有效性，至于在其他岩土领域的变形预测效果，仍需今后进一步研究。