τ-p变换在隧道地震超前探测中的应用及适应性分析
2018-07-10陈宇波付志红
周 结, 陈宇波, 王 耀, 付志红, 周 密, 廖 先
(1. 重庆大学电气工程学院, 重庆 400044; 2. 中国建筑第五工程局有限公司, 湖南 长沙 410083;3. 重庆璀陆探测技术有限公司, 重庆 402660; 4. 国网重庆市电力公司电力科学研究院, 重庆 401123)
0 引言
隧道超前探测主要利用地球物理方法获取隧道掌子面前方地质信息,其中,地震反射波法能够进行超长距离精细探测(大于100 m),已成为隧道超前探测的主流方法[1]。其基本原理是在隧道内激发地震波,该波主要以体波的形式向前方传播,遇到地质界面地震信号反射,由布置在隧道一边且与岩壁耦合较好的三分量传感器接收反射波,通过分析反射波场获取掌子面前方的地质情况。
为提高探测的精度,降低多解性,充分利用地震反射全波场信息,隧道地震超前探测引入了多分量地震检波器。通过三分量检波器接收反射波,包括反射纵波和反射横波,在数据处理时需将所采集数据中的纵、横波等相互混杂信息分离进行联合预报。
地震波场分离方法在地面地震勘探和井中地震(VSP)中应用较为广泛,其主要思路是将地震数据通过一定的方法变换到一个新的域。在新的域中,将不同波场分离,然后进行反变换,主要包括中值滤波法、奇异值分解法、极化滤波法、F-K变换法和Radon变换法等[2-7]。
隧道内为全空间,且观测系统与常规地面地震勘探存在一定差异,需针对性研究其波场分离方法。关于隧道地震超前探测波场分离方法,沈鸿雁等[8]提出了一种联合F-K变换与τ-p变换实现隧道和井巷波场分离的新思路,即考虑到在下行波能量较强时,先使用F-K变换削弱部分下行波,再使用τ-p变换精确提取上行波,以克服τ-p变换的假频和端点效应;王朝令等[9-10]通过模拟复杂条件下隧道地震全波场,定性地分析了反射层倾角与隧道轴线交角大于45°时τ-p变换和F-K变换的有效性;葛文等[11]将自适应极化滤波方法应用于隧道超前探测,利用极化特性成功地分离了前方构造倾角为30°时的反射纵横波,但该方法难以区分前方和周围的反射波,实用性较小。
本文以研究隧道地震超前探测波场分离的有效性为目标,从时距曲线出发,分析推导了隧道内线性观测系统时距曲线特性,利用Taylor变换公式对该时距曲线做线性近似处理。首次提出τ-p变换截距和慢度与反射层倾角的关系,分析τ-p变换的物理意义,并通过定量计算,分析不同倾角对Taylor变换后的时距曲线误差的影响,通过模型试算进行验证分析,并给出实例应用。
1 τ-p变换
τ-p变换即线性Radon变换[12],Radon变换的思路是对时距域地震数据沿着某一特定曲线进行叠加求和,将其变换到Radon域。Radon变换包括τ-p变换、τ-q变换和双曲型Radon变换,其叠加路径分别是直线、抛物线和双曲线,本文仅研究τ-p变换。
对于连续排列,τ-p变换

(1)
(2)

时间域的τ-p变换在变换后能量发散,得到的反变换地震信号失真较为严重。考虑使用频率域最小平方法τ-p变换[12-13],对连续排列的时间域τ-p变换公式进行傅里叶变换,得到频率域变换公式

(3)
(4)
V=LU,
(5)
(6)
式(5)—(6)中:L=ejωpj′xi,i=1,2,3…,m,j′=1,2,3…,n;LH=e-jωpj′xi,i=1,2,3…,m,j′=1,2,3…,n。
用最小平方法求解可得频率域τ-p正变换公式
V=(LLH)-1LU。
(7)
为平滑τ-p变换,加入阻尼因子μ,则有
V=(LLH+μI)-1LU。
(8)
在频率域最小平方τ-p变换中由于采用固有的阻尼因子,其分辨率受限,为提高分辨率,本文采用变阻尼τ-p变换,即高分辨率τ-p变换[13]
Vk+1=(LLH+WWH)-1LVk。
(9)
式中:Vk、Vk+1分别为第k和k+1次τ-p变换域的值;W为与Vk相关的对角矩阵。
高分辨率τ-p变换为迭代方法,初值可由最小平方τ-p变换获得,通过几次迭代即可获取满足一定高分辨率的τ-p变换域。
2 反射波时距曲线特性
时距曲线指地震波走时与距离的关系,由于地面地震勘探与井中地震(VSP)假设的水平地层模型时距曲线特性在隧道超前探测下无法适用,本文研究了隧道内的反射波时距曲线特性。为便于分析,采用图1中满足炮检互换原理的TSP系统等价排列,在隧道一侧布置1个炮点,由24个等间距的检波器排列接收地震波。该观测系统与线性τ-p变换理论一致,能够较好地进行波场分离,而其他观测系统(TRT系统、TST系统等)由于采用非线性排列,波场分离相对比较困难。

a为炮检距;b为检波器与掌子面的距离;h为隧道掌子面到低速带左边界的距离;w为低速带的宽度。
图1隧道超前探测模型
Fig. 1Tunnel seismic advance prediction model
首先,给出图1模型低速带左边界的反射纵横波时距曲线
(10)
式中:t为地震传播时间;v为背景纵横波速度,以炮点为坐标零点;x为检波器位置;s为隧道掌子面轴线前方的反射界面位置;α为反射界面与隧道轴线夹角。
对式(10)进行一阶Taylor展开,得到反射纵横波时距曲线的一阶Taylor展开式
(11)
式中tt为一阶Taylor展开式反射纵横波传播时间。
比较式(11)与τ-p变换叠加直线公式t=τ+px,有如下对应关系
(12)
(13)
式(12)—(13)中:τ为炮点处反射纵横波自激自收传播时间;p为反射纵横波倾斜慢度。
对于一阶Taylor展开方法的可行性,推导发现反射纵横波时距曲线误差相同
(14)
由式(14)可知,时距曲线误差与纵横波速度无关,仅与反射面位置倾角和检波器位置有关。根据隧道超前探测施工规程,取x为15~49.5 m,间隔为1.5 m,掌子面在69.5 m处,计算h为0~150 m、α为10°~90°时的视速度曲线误差。
反射波时距曲线一阶Taylor近似误差见图2。当α为10°、h为0 m时,误差最大,达17.5%,此时一阶Taylor近似与原始反射波时距曲线差别较大。随着α和h逐渐变大,误差逐渐变小,最小为0。图中时距曲线误差小于1%的区域定义为有效区域,误差大于1%的区域定义为无效区域。
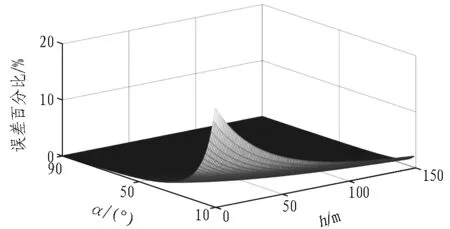
图2 反射波时距曲线的一阶Taylor近似误差
Fig. 2First order Taylor approximation error of time-distance curve of reflected wave
反射波时距曲线的一阶Taylor近似临界见图3,即近似误差为1%时反射面的距离h与倾角α的关系曲线图,此时的α为有效区域的最小有效值。当h为0 m,最小有效α为40°;当h为150 m,最小有效α为15°,即随着h增大,最小有效α逐渐变小,有效区域变大。

图3 反射波时距曲线一阶Taylor近似有效区域临界图
Fig. 3Critical graph of effective area of first order Taylor approximation error of time-distance curve of reflected wave
线性τ-p变换理论上是对无限(t,x)集合的线性变换,而反射波时距曲线一阶Taylor展开式是对时距曲线进行线性近似,略去非线性特性。当反射界面与隧道轴线垂直时,时距曲线是线性的,一阶Taylor展开式无误差;而当反射倾角逐渐变小,时距曲线为双曲线,非线性逐渐严重,一阶Taylor展开式误差越来越大。线性τ-p变换则是对原始数据的线性变换,并无误差,因此τ-p变换与一阶Taylor展开式为非线性与线性的差异。分析表明,在有效探测距离范围内,一阶Taylor近似反射波时距曲线在反射界面倾角大于40°时误差小于1%,能够较好地进行τ-p变换,τ-p变换理论上符合隧道超前探测的反射纵波和反射横波时距曲线模型。
3 波场分离模型试算
按照图1隧道超前探测模型进行正演模拟,取背景场纵波速度为4 000 m/s,横波速度为2 310 m/s;震源与检波器位于隧道同侧的一条测线上,炮检距a为15 m, 24个检波器间距为1.5 m,检波器与隧道掌子面距离b为20 m,隧道掌子面到低速带左边界的距离h为10 m,低速带宽度w为30 m,低速带纵波速度为2 500 m/s,横波速度为1 450 m/s。地震子波采用Ricker子波,主频为400 Hz,采用时间为0.05 ms,采样慢度为1×10-5s/m,分别模拟低速带倾角为90°、60°、30°情况下的波场记录,并进行τ-p变换波场分离。
低速带倾角为90°、60°和30°时检波器排列接收到的记录分别见图4(a)、5(a)和6(a),由水平分量与垂直分量合成,横坐标为道号,代表不同检波器,纵坐标为时间,其中,A为直达纵波,B为直达横波,C为低速带左边界反射纵波,D为低速带左边界反射横波,E为低速带右边界反射纵波,F为低速带右边界反射横波,G为低速带左边界反射转换横波,H为低速带右边界反射转换横波。由于检波器接收信号顺序的不同,直达波信号与反射波信号具有相反的同相轴走向。图4(a)示出倾角为90°时的时域记录,由于直达波垂直入射至低速带,无转换波产生。观察图5(a)和图6(a),随着低速带倾角越来越小,逐渐产生转换波,且反射波到达时间减小,反射波信号逐渐上移,低速带右边界反射纵波与左边界反射横波开始相互混杂,尤其当低速带倾角为30°时,反射信号混杂尤为严重,左边界反射横波D与右边界反射纵波E难以分辨。

(a) 时域信号(b)τ-p域信号
图490°倾角时变换记录图
Fig. 4Transform record when dip angle is 90°

(a) 时域信号(b)τ-p域信号
图560°倾角时变换记录图
Fig. 5Transform record when dip angle is 60°
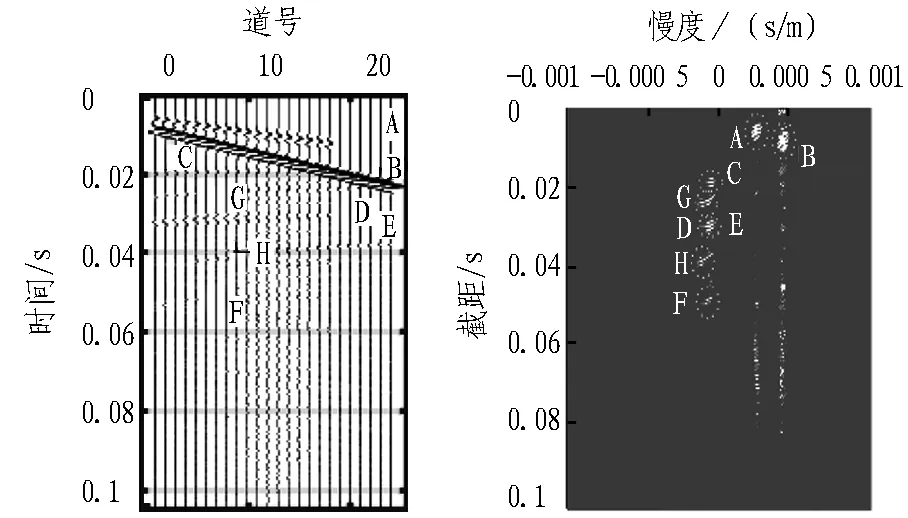
(a) 时域信号 (b)τ-p域信号
图630°倾角时变换记录图
Fig. 6Transform record when dip angle is 30°
时域记录τ-p变换后的τ-p域记录见图4(b)、5(b)、6(b),为便于显示,τ-p变换图均做白化处理,横坐标为慢度,即视速度的倒数,纵坐标为截距,即自激自收时间。在τ-p域中,直达波与反射波表现为能量团,直达波位于正慢度象限,反射波位于负慢度象限。由于反射纵波与反射横波具有不同的慢度,各自位于互不相关的区域,能够清晰地分辨。随着倾角α逐渐变小,反射波逐渐向正慢度方向移动,且由于反射纵波速度比反射横波大,慢度变化小,反射转化横波能量团逐渐向反射纵波能量团靠近,使得分离变得困难。表1是根据式(14)计算的一阶Taylor近似反射波视速度值和模型数据τ-p变换后根据能量团提取的视速度值。随着倾角α减小,视速度值均变大,由于Taylor展开,实际资料提取的视速度比一阶Taylor近似计算的值大,且相对误差变大,同时由观察发现,反射横波相对误差更小。

表1 不同倾角低速带反射波视速度
按照表1中计算的一阶近似视速度值进行波场分离,选择分离范围为±500 m/s。图7—9分别示出低速带倾角为90°、60°和30°时的时域记录τ-p变换分离后的纵横波分量,其中图7(a)、8(a)和9(a)是纵波分量图,图7(b)、8(b)和9(b)是横波分量图。在倾角为90°和60°时,纵横波分离效果均很好,无直达波残余,且没有相互干扰。观察图8(b),在倾角为60°时,横波分量中主要是反射横波,转换横波能量较弱;在倾角为30°时,由于此时一阶近似反射纵横波视速度相对误差很大,纵横波分离效果变差。对比分离的纵波分量和横波分量,发现横波的分离效果相对要好一些。横波分量中主要是转换横波,纵波分量中有较大的横波分量,这是由于尽管一阶近似反射横波视速度相对误差随着倾角变小而变大,但对于相同反射倾角时的反射纵波,其相对误差更小,分离效果比反射纵波好。

(a) 纵波 (b) 横波
图790°倾角记录波场分离后的纵横波分量图
Fig. 7Primary and secondary wave after wavefield separating when dip angle is 90°
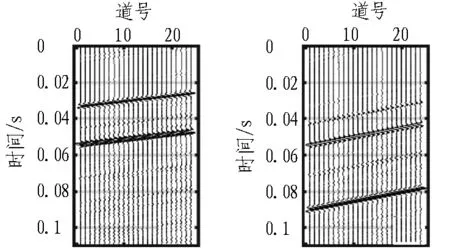
(a) 纵波 (b) 横波
图860°倾角记录波场分离后的纵横波分量图
Fig. 8Primary and secondary wave after wavefield separating when dip angle is 60°
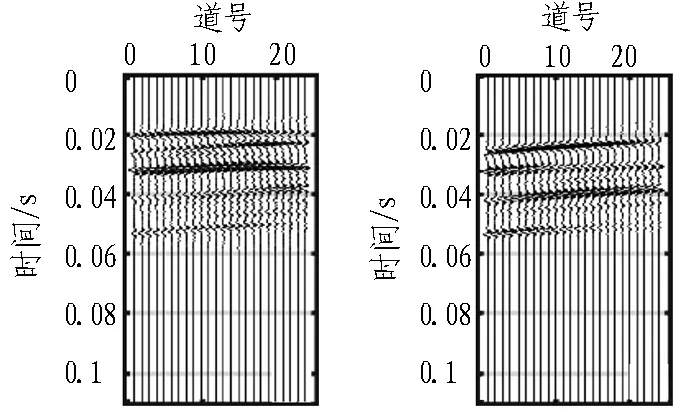
(a) 纵波 (b) 横波
图930°倾角记录波场分离后的纵横波分量图
Fig. 9Primary and secondary wave after wavefield separating when dip angle is 30°
4 应用实例
湖南吉首某隧道地震超前探测的实际资料及波场分离见图10和图11,使用TETSP-2隧道超前预报仪进行数据采集,仪器采用高灵敏度加速度传感器,灵敏度为2.5 V/g,采样率为192 kHz。实测下采样率为32 kHz,炮间距1.5 m,对原始信号进行道均衡,扩散补偿等预处理,然后拾取初至,得直达纵波速度为5 100 m/s,横波速度为2 940 m/s。时域信号为水平分量记录,见图10(a)。能够观测到明显的直达纵波和直达横波,但反射纵横波完全混杂在一起且被较强的直达波压制。对时域信号进行τ-p变换,根据拾取的纵横波速度,假设反射界面为90°倾角,取±500 m/s为波场分离的速度范围,在τ-p域中,根据该范围确定慢度范围,可推测纵横波分量分别位于S和P区域,见图10(b)。图11(a)、11(b)示出分离后的纵横波,图11(a)中0.01 s至0.04 s间存在多个纵波反射波组,根据拾取的纵波速度进行计算,能够大致判断0.01~0.03 s的波组来自隧道周围和掌子面, 0.03~0.04 s的波组来自掌子面前方50 m左右的反射区域。实际开挖的过程中,在隧道掌子面前方50 m左右发现溶洞(见图12),该区域对应较好。图11(b)中的多个横波反射波组,根据拾取的横波速度进行计算,其主要来自于比较靠前的反射区域,不能够做有效的预测。总体上,本次预报具有一定的效果,纵波对应较好,横波对应较差。由于按照90°倾角假设进行纵横波波场分离,获取的纵横波分离速度范围具有一定的局限性,且实际地震波传播情况比较复杂,地震波吸收衰减比较严重,故而信噪比较低,波场分离效果一般。

(a) 时域信号 (b)τ-p域信号
图10实际资料变换
Fig. 10Transform record of real data
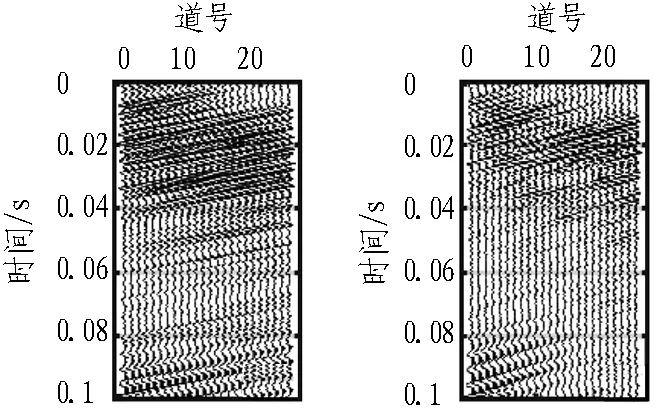
(a) 纵波(b) 横波
图11实际资料波场分离后的纵横波分量图
Fig. 11Primary and secondary wave of real data after wavefield separating

图12 隧道开挖溶洞图
5 结论与讨论
本文对隧道内反射纵横波的时距曲线进行一阶Taylor展开,计算了有效探测距离范围内一阶Taylor近似时距曲线的相对误差。通过模型试算验证了反射倾角大于40°时τ-p变换的可行性,并计算了视速度误差。分析表明,视速度误差对于波场分离效果影响比较大,当反射界面与隧道轴线夹角比较小时,反射波的视速度非线性严重,不同检波器位置的视速度跨度比较大,由负视速度逐渐向正视速度转移,视速度误差比较大,此时波场分离不完全,致使纵横波分离均有残余成分。在实际预报中,由于纵横波速度不同,残余部分会产生假的反射界面,影响预报的准确性。
在τ-p域中慢度与反射倾角和波速同时相关。在实际应用中,由于地质环境的复杂性,当反射界面倾角未知时,仅能够作90°倾角假设,依靠波速确定纵横波视速度分离范围,具有一定的局限性,今后可进一步对反射界面预测作研究。
