激活学生思维使学生自主学起来

□ 海南省洋浦中学 王晓虎

要使数学课吸引学生，就要想办法激发学生的思维，使学生的脑子动起来，让学生主动参与，把知识学活，通过应用，变成能力，改变从我们的课堂做起，以下的几个案例使我印象深刻，促使我反思。

一、把数学与学生感兴趣的问题联系在一起，能激发学生的思维，使学生主动参与

在学必修三的互斥事件时，我选了这样一道例题，例：小明的自行车用的是密码锁，密码锁的四位数密码由4个数字2、4、6、8按一定顺序构成。小明不小心忘记了密码中4个数字的顺序，试问：随机地输入由2，4，6，8组成的一个四位数，不能打开锁的概率是多少？

在我的启发下，同学们通过画树形图，找出基本事件的总数，利用对立事件的概率关系求出了所要的结果。这时我将题目进行了如下变式：1.如果只记得最后一个密码是8，那么随机输入2、4、6、8组成的一个四位数，不能打开锁的概率是多少？问题一提出，很快班长黄朝相就站起来，只见他说：从反面思考是1/6，并上黑板画出了树形图。看其他同学的表情，对此问题有一定的兴趣，我开始了再变式：2.如果小明只记住了密码中的三个数2、4、6，那么随机地输入由2、4、6和其他一个数字组成的一个四位数，不能打开锁的概率是多少？此时同学们陷入了深思：到底应该是多少呢？不久李城玑给出了解答，正面是1/60，要求的答案自然是59/60，我让李城玑上黑板用图形来表示其想法，做着做着同学们看出了破绽，陈丰站起来说：“老师并没有说，2、4、6是前三个密码，不知道的这个数是哪个位置并不确定。”这一点拨，李城玑沉思了，过了一会儿大家都想到了此题的答案。我随机一想，在洋浦的没有人不知道彩票的，彩票中不是也有这些问题？我就依彩票来进行变式。变式1：大家知道彩票也是由四个数字组成的，这“万字图”是怎么来的，谁能上来给大家说清楚？变式2：假定知道一等奖的个位数是2，百位数是5，要买中一等奖，最多需要买多少张？变式3：如果知道一等奖，有2、3、6同上，要买中一等奖，最多需要买多少张呢？学生对这几个问题非常感兴趣，在讨论中常常是不断纠正，完全忘了这是在上课，而且学生还生发出了不同的问题，看看就要下课了，学生还在探究……

学生对问题的好奇，积极参与研讨，思维被充分激活，还原了数学课的本来面目。

二、让学生经历知识的发生、发展过程，来激发自主学习的能力

以问题做先导，以思维为拐杖，带领学生去经历公式、定理产生、发展的过程，重温前人发现公式、定理的喜悦，体验公式、定理的魔力所在。如在余弦定理的教学中，我是这样进行的：首先，我提出问题，在RtABC中，已知A是直角，则BC2=AB2+AC2，如果A不是直角，而是锐角或是钝角，能否由A和AB、AC来求BC呢？勾股定理是学生再熟悉不过的定理，引导学生思考将不熟悉的问题转化为熟悉的问题也是我们数学中常用的思想方法，学生自然想试试。

如图：当A是锐角时，怎样才能转化为直角三角形呢？当然是过B向AC作垂线交AC于D。

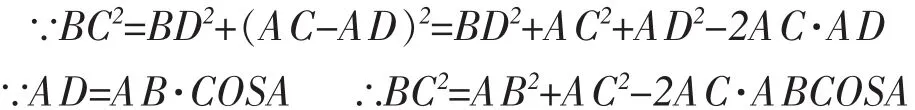
如果A是钝角呢？又该怎么做呢？启发学生再一次去构造直角三角形，转化论证。

学生在教师的启发引导下，从原有的知识出发，将不熟悉的情形向熟悉的情形转化，通过自己的思考推出了余弦定理，体验到了成功的快乐。这时我再一次让学生思考，余弦定理和勾股定理有什么关系？既然勾股定理是余弦定理的特例，我们能否借助余弦定理去判断一个三角形是锐角三角形还是钝角三角形呢？怎么判定？

一节课我只是让学生得出了定理和解决了几个问题，没有让学生去机械地记定理、用定理。借助问题对学生思维一次又一次被激发，学生始终沉浸其中，深度参与，获得了数学发现的快乐，体验了豁然开朗的顿悟，学生怎能厌倦？

三、对问题做深层次的发散、变式，在变幻莫测中激发学生的自主学习

在学数计数的加法原理与乘法原理时，解题时怎样做到不重不漏是个难点，而若以大量的题去机械训练，学生既感到枯燥乏味，又难以理解。于是我设计了一道例题， 从 0、1、2、3、4、5 这五个数字中任取两个数字求积，可得多少个不同的结果？我让学生先解。

学生甲：解：A×B,若其中一个取0，另一个取其他数，则只能得一种结果0；A与B不取0，则有5×4种，所以共有21种结果。

对吗？有重复的吗？在我的启发下，有人举手了。

学生乙：不对，有重复的，1×2 和 2×1，2×3 和 3×2,等等，是相同的。

相同的有多少呢？我再一次提问。学生很快得出有10个。我看学生兴趣浓，抓住时机，进行变式，1.改为求商呢？2.改为求差呢？3.改为求和呢？

从非常简单的问题介入，在变化中引发学生的兴趣，环环紧扣，层层深入，解题中又常常出现一些“意外”，学生在不知不觉中被深深吸引，沉浸其中，兴趣盎然。

能深深吸引学生，激发学生自主学习，主动思考的课堂，才充满浓浓的数学味道，而要达到这样的效果，需要我们对教材进行深入的思考、挖掘，对数学的应用进行不断地琢磨，对好的问题情景不断地积累，把数学课堂变成学生主动思考，体验成功快乐的地方，促使学生思维之花不断绽放。