轮轨几何接触点的人工神经网络快速计算方法

杨 光 ，杨 岳，易 兵，刘文龙，吴永军

（中南大学 交通运输工程学院，长沙 410075）

车轮踏面与钢轨的接触点计算是研究轮轨关系的基础，是评价轮轨接触性能的一个重要指标。迹线法[1]是计算轮轨接触点的经典方法，并随着部分学者对其进行不断地改进[2-3]，现已成为计算精度高、公式推导完备的成熟算法。当运用该方法求解轮轨接触点时，需首先对钢轨廓形进行样条曲线拟合，再进行复杂的数值计算，过程较为繁琐。针对这一弊端，本文利用三层前馈反向传播神经网络，实现不同廓形条件下轮轨接触点的快速计算。采用NURBS方法进行钢轨廓形的参数化建模，通过权因子修改对钢轨廓形精确调整。在此基础上，构建轮轨几何接触点的神经网络模型，结合迹线法对不同廓形条件下的轮轨几何接触点进行计算，得到钢轨廓形与接触点关系的样本。对所搭建的轮轨几何接触点神经网络进行训练，获得的神经网络可实现不同钢轨廓形下轮轨接触点的快速计算。

1 钢轨廓形的参数化建模

1.1 NURBS曲线定义

一条p次NURBS曲线[4]的定义为：

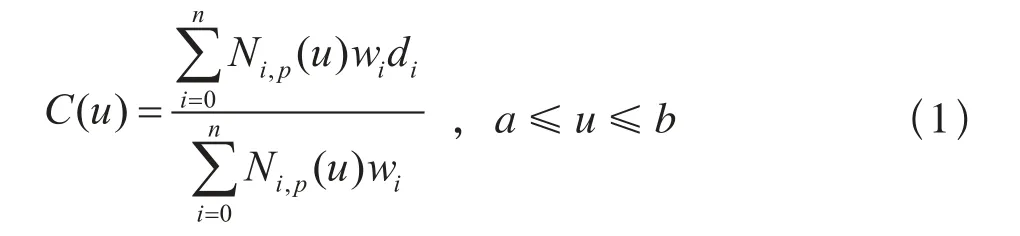
其中，di(i=0, 1, …, n)为控制顶点，将其顺序相连即可构成控制多边形；wi(i=0, 1, …, n)为权因子；Ni,p(u)为定义在非周期（且非均匀）的节点矢量U上的p次规范B样条基函数，并且：

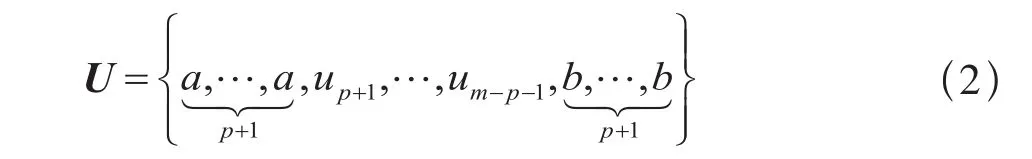
当节点数为m+1，控制点个数为n+1，幂次为p时，m、n、p三者的关系为m=n+p+1。在实际应用中，一般取a=0，b=1，故曲线的定义域为u∈[up,un+1]=[0, 1]，并且对所有的i，都有wi＞0。若令：

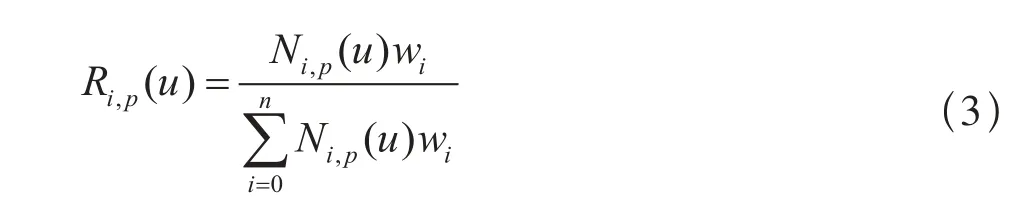
那么，式（1）则可改写为：

在此，将Ri,p(u)称为有理基函数，即u∈[0, 1]上的分段有理函数。

1.2 钢轨廓形的参数化建模

通常，三次NURBS曲线即可满足工程应用的需求。根据上述曲线建模理论，以CHN60钢轨为实例，利用三次NURBS曲线对钢轨廓形进行参数化表示。按图1所示，以钢轨轨顶中心为原点，以水平方向作为横轴，垂直方向作为纵轴建立二维参数化建模坐标系。

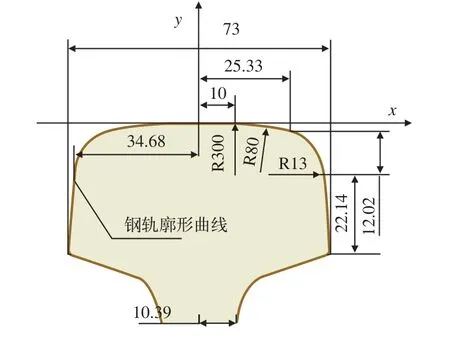
图1 标准CHN60钢轨廓形

标准钢轨廓形上任意的型值点坐标均可通过数值计算的方法得到。在此，以等间距取点的方法在钢轨廓形上选择17个点作为NURBS曲线的型值点，具体数值如下：

得到钢轨廓形的型值点后，可采用累积弦长参数法计算曲线的节点矢量，其节点矢量U满足：

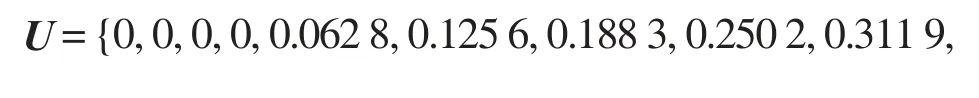
通过该组型值点的NURBS曲线控制点可由NURBS曲线插值法反求得到[5]。经反算，钢轨廓形三次NURBS曲线的19个控制点坐标如下：

预设各控制点处的NURBS曲线权因子wi=1（i=0, 1, …, 19）。根据NURBS曲线的定义，在得到节点矢量U、控制点d和对应的权因子w后，即可实现钢轨廓形的参数化表示，其建模效果如图2所示,其中折线为由NURBS控制点所构成的控制多边形,光滑曲线为基于NURBS的参数化钢轨廓形曲线。

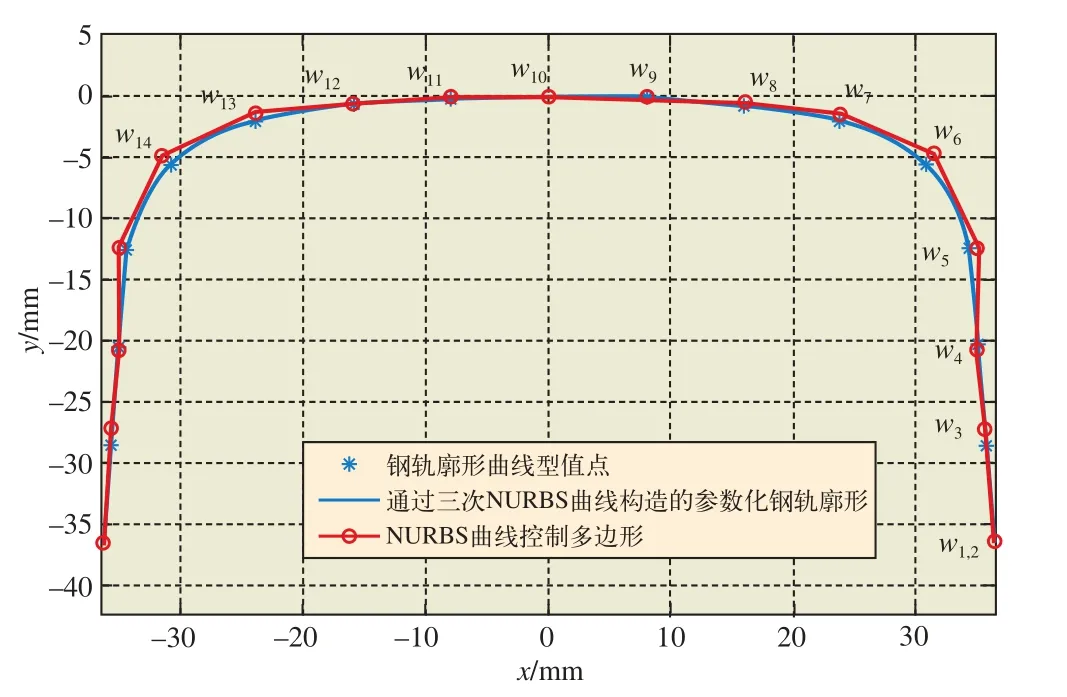
图2 钢轨廓形的参数化表示

需要对钢轨廓形进行微调时，可采用修改相应控制点权因子的方法对NURBS曲线进行调整。根据最优拉丁超立方抽样方法，将NURBS曲线控制点权因子wi的变化区间设定为[0,2][6]。具体调整方法可参考文献[7]，在此不再赘述。

2 基于BP神经网络的轮轨几何接触点计算

2.1 轮轨几何接触点的BP神经网络模型

BP人工神经网络是一种模仿人类大脑神经网络结构及功能的信息处理模型，其训练方式为误差反向传播，以均方误差最小为目标不断修改权重和阈值[8-9]。为了实现不同廓形下轮轨接触点的快速计算，搭建如图3所示的三层前馈反向传播神经网络。

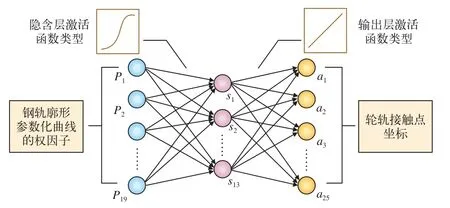
图3 轮轨几何接触点的人工神经网络结构

将控制钢轨廓形的19个权因子作为输入层的神经元P={p1, p2, p3, … , p18, p19}。设定隐含层神经元个数为13个，即S = {s1, s2, s3, …, s12, s13}，每个神经元的阈值为(k=1, 2, …, 13)。设定轮对横移量的取值范围为–12～12 mm内的整数，并将通过迹线法计算出的轮轨几何接触点坐标对作为输出层神经元A = {a1, a2, a3, …, a24, a25}，每个神经元的阈值为(j=1, 2,…, 25)。在轮轨几何接触点神经网络中，层与层之间的联系，是由相应的连接权值W及激发函数f进行控制的。用，i表示输入层第i个神经元pi与隐含层第k个神经元sk之间的连接权值；用，k表示隐含层第k个神经元sk与输出层第j个神经元aj之间的连接权值。其中，∈[–1, 1]。设定隐含层激发函数为S型曲线传递函数，输出层激发函数为线性传递函数，即：

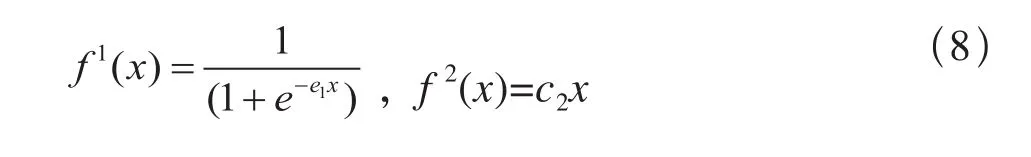
在轮轨几何接触点的BP神经网络中，后一层神经元的输出值均是通过对上一层输入的每个神经元的值进行加权求和后，结合阈值与激发函数后得到的。那么，输出层第j个神经元的输出值可以表示为：

2.2 BP神经网络的训练算法

轮轨几何接触点的人工神经网络模型构建完成后，还需结合轮轨几何接触点样本对各连接权值W和阈值b进行训练。首先对W和b在其定义域[–1, 1]内进行随机赋值，即实现神经网络的初始化，再将规模为m的训练样本输入神经网络。在训练过程中，应对输出层输出的轮轨接触点a，与期望输出的轮轨接触点r进行比较，并计算全局误差：

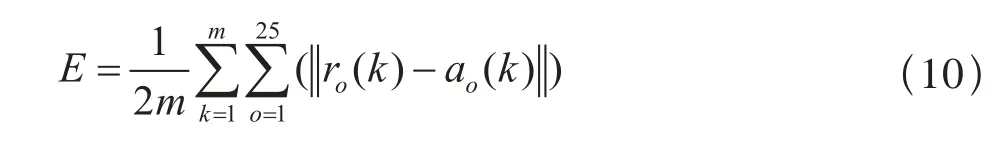
若计算出的全局误差E不满足许用误差ε的要求，则从输出层开始以梯度下降的方式反向调整权值，其调整公式如下：

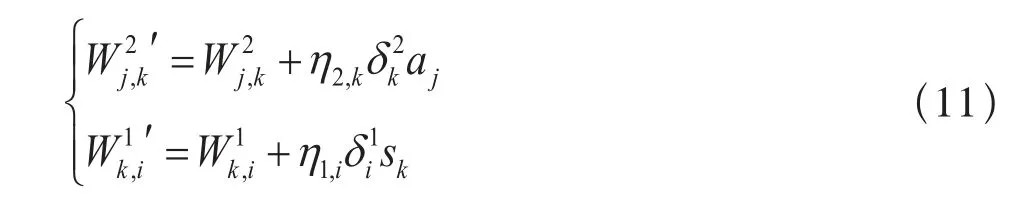
其中，为全局误差函数对输出层与隐含层连接权重，k的偏导数；为全局误差函数对隐含层与输入层连接权重，i的偏导数。

通过上述方法即可实现对各层连接权重W的不断修正，当全局误差E收敛于许用误差ε的要求时，完成BP神经网络的训练。轮轨接触点计算的BP神经网络训练流程可归纳 ，如图4所示。

图4 轮轨接触点的BP神经网络训练

3 计算实例与结果分析

3.1 网络的训练情况

设定左右车轮内侧距为1 353 mm，轨距为1 435 mm，轨底坡和摇头角均为0，轮对为标准LMA型车轮踏面，轮对横移量l的取值为–12～12 mm内的整数。在[0, 2]内随机调节19个NURBS曲线权因子的值，即可得到多组不同的钢轨廓形曲线。不同廓形在横移量范围内的轮轨接触点位置均可以由迹线法计算得到。

为了实现轮轨接触点神经网络的良好训练，构造了2 000组不同廓形下的轮轨几何接触点分布情况作为训练样本。其中，90%的样本用于BP神经网络的训练，5%的样本作为验证，另外5%的样本仅用于对所训练网络的性能进行独立测试，不影响训练过程。选用MATLAB 2012b软件作为神经网络算法的实现平台，PC计算机CPU为Intel(R) Pentium(R)Dual CPU E2220 @2.40 GHZ。在训练过程中，均方误差随迭代次数的增加而呈下降趋势。并且在第102次迭代时均方误差达到收敛，在迭第96次迭代时均方误差最小，约为4.57，训练收敛速度快。

在神经网络训练完成后，需要用验证组样本来进行拟合优度的检验。其中，神经网络的输出值与目标值间的相关性可通过二者的相关系数R进行判断，R越接近于1，表示二者相关性越强，差距越小。经计算，本文构建并训练的BP神经网络相关系数达到0.988 49，十分接近1，拟合效果理想。

3.2 计算实例及分析

为了更加直观地对轮轨几何接触点在不同横移量条件下的预测效果进行评价，另取一组未参与网络训练及验证的数据进行计算的精度分析。所选取实例的输入权因子向量为：

在上文所设定的工况下，基于BP神经网络的轮轨几何接触点的计算结果见图5a，根据迹线法计算所得到的轮轨几何接触点分布情况见图5b。

图5中，轮轨间的连线代表了某一横移量下车轮踏面和钢轨廓形的接触位置。为了对预测结果进行深入的误差分析，表1列出了部分横移量条件下，两种方法在钢轨廓形上的接触点计算结果对比。

根据表1和图5，当横移量在–12～5 mm和9～12 mm的范围内时，本文所构建的BP神经网络算法与迹线法所得到的结果十分近似，平均误差为0.168 3 mm。由于轮轨外形特征，当横移量在5～9 mm时接触点对在轮轨型面上的分布间隔距离较远，神经网络计算所得结果与迹线法结果相比平均误差稍大，约为0.470 5 mm。该组样本总体预测结果的平均误差约为0.232 5 mm，总体预测效果良好，能够满足工程实践要求。另外，针对上述实例，迹线法的计算时长为14.331 2 s，BP神经网络方法的计算时长为2.148 1 s。采用本文所提出的人工神经网络算法能够将计算时长缩短约7倍，明显提升轮轨接触点计算的效率。

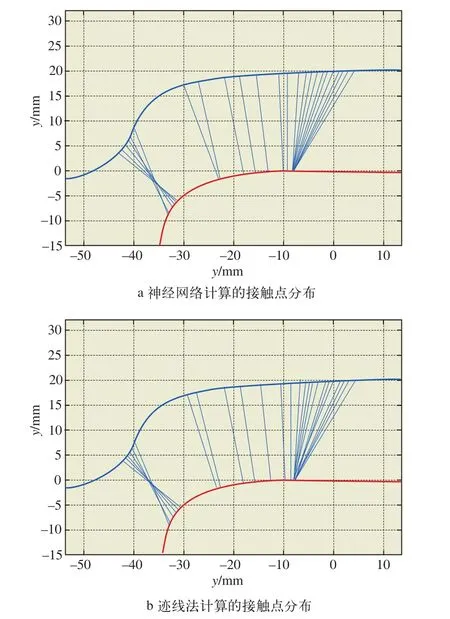
图5 轮轨接触点位置分布对比

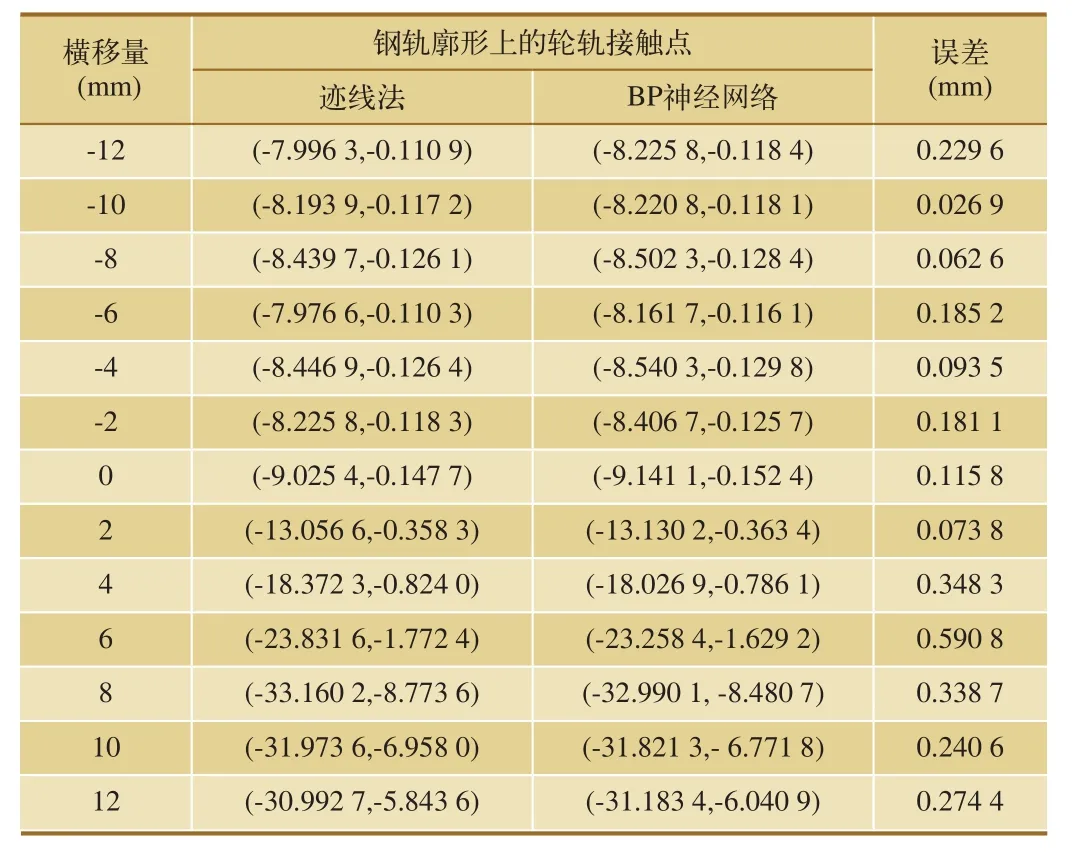
表1 轮轨接触点计算结果对比

4 结束语

本文建立了一个用于计算轮轨几何接触点的人工神经网络，测试样本的网络输出值与目标值的相关系数为0.988 49，表明所建立的模型是可靠的。将一组未参与训练及验证的权因子样本数据输入训练后的BP神经网络中，其结果与通过迹线法计算所得结果的总体平均误差为0.232 5 mm，预测精度高。另外，相较于迹线法，人工神经网络算法的计算时长缩短约7倍，有效提升轮轨接触点的计算效率。

：

[1] 王开文.车轮接触点迹线及轮轨接触几何参数的计算[J].西南交通大学学报，1984（1）：89-99.

[2] 张卫华.空间状态轮轮(轨)接触点计算方法[J].中国铁道科学， 2006（4）：76-79.

[3] 倪平涛,刘德刚,曲文强.轮轨与轮轮接触几何计算研究[J].铁道机车车辆，2012（5）：5-9.

[4] 邓培森，陈绍平，沈均成.三次NURBS曲线相关积分量的精确计算公式及其应用[J]. 武汉理工大学学报：交通科学与工程版， 2014，38（3）：652-657.

[5] 陈绍平.三次NURBS曲线的插值与应用[J].机械科学与技术， 2001，20（5）：692-693.

[6] 曾 威.钢轨打磨廓形多目标优化设计方法研究[D].长沙：中南大学，2016.

[7] 张国华，杨兴强，张彩明.基于权因子的NURBS曲线形状调整[J]. 计算机辅助设计与图形学学报，2004，16（10）：1396-1400.

[8] 程清波.基于BP神经网络的铁路客运设备故障监测模型设计与研究[J].铁路计算机应用，2016，25（2）：3-6.

[9] 汪健雄.基于大数据平台的动态票额智能预分系统的研究与实现[J].铁路计算机应用，2016，25（9）：31-37.