基于RAMS的地铁信号系统维修策略研究

莫志刚，骆汉宾

（华中科技大学 土木工程及力学学院，武汉 430074）

设备的失效方式既有统一性也有差异性。统一性是指同类的设备拥有相同或近似的失效形态；差异性是指不同设备或者同类设备在不同的环境下呈现不同的失效形态。因此，需要对不同设备或者不同环境下运作的同类设备进行区分，采取合适的维修方式。在某个设备生命周期的某个阶段，对其采取的维修工作可能是多种维修方式的有机组合。

轨道交通信号系统在日常运营过程中，可靠性、可用性及安全性都需要维持在一个较高水平，对于整个系统的运营效率和效益而言，并不只有可靠性一个优化目标，还需要考虑其可用性、安全性以及维护工作中所产生的费用，因此，这个问题的研究就可以归类为一个多目标优化问题，决策人员能够利用计算结果来加强决策指令的准确性与合理性，制定一个合理可行的维修策略，实现上述4个参数有机结合[1-4]。本文以南宁轨道交通信号系统的关键设备为例，求解多目标问题的最优解集，为运营维修决策提供有效的数据支持。

1 多目标优化问题理论研究

多目标优化[5-11]（MOP，Multi-objective Programming）的算法旨在解决超过1个目标函数时，如何获取整体最优解的问题。在目标函数之外，一般会出现1个以上的约束条件，通常可以描述为以下形式：

其中， Z=[z1, z2,…, ze, …, zE]（E 维决策向量），是在计算最优解时的搜索空间；S与f(Z)是各目标函数的集合，包含N个研究对象；两类约束函数可表示为gi(Z)≤0和hj(Z)=0，是所有解必须符合的条件；ze_1和ze_2是各维数据执行搜索时能达到的边界。

假设求解问题包含的若干优化目标存在矛盾，无论进行何种操作或整合，当我们试图追求目标1达到最佳理想状态时，极有可能导致目标2（或另外更多的目标）无法达到最佳理想状态。这类问题中，唯一能够进行的便是若干目标相互妥协，妥协后得到的各个有效解也称为Pareto最优解（或称为非劣最优解）。通常，最优解并不是单独的一个数值，往往是大量数值的组合，在坐标系中能够看到是大量的点集。对于运营人员来说，则可以依照实际需要来明确哪个或者哪些点属于他们需要的最优解。

最优解使用数学语言描述为：无法被该集合中的任何点描述的点。整个搜索空间中一定不存在这样的Z，能够令fn(Z)≤fn(Z*)成立，其中， n=1, 2,…,N, Z*是多目标优化问题的全局最优解。在计算过程中得到的这一类解的集合，就定义为有效解集。

2 目标优化模型及参数定义

本研究考虑在地铁信号系统设备维修活动中，系统可靠性与可用性、安全性以及维修费用共同作用下的多目标优化问题。优化目标为系统的平均可靠性和系统维修费用，约束条件为系统的技术可用度和安全性。

2.1 目标函数

（1）系统平均可靠性

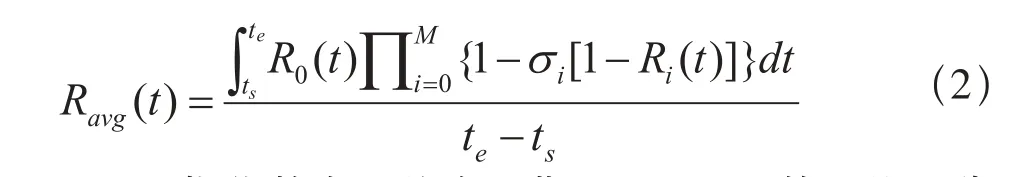
Ravg(t)指代整个系统在周期t∈(ts, te]的平均可靠性，其中，R0(t)表示整个系统除关键部件外其他部件所构成的综合可靠性；Ri(t)表示系统中关键部件i的可靠性；σi表示整个系统发生故障的前提下，由于i部件发生不能接受的不正常运转引起的概率；M表示整个系统中所有符合关键部件定义的部件总数量。

（2）系统维修费用

维修费用是维护工作在制定计划时应着重考虑的一个因素，它的合理与否在很大程度上显示出相应维护计划的优劣。根据设计参数、生产环境及运营实际得到的经验数据，可以对信号系统的各个设备构造一个费用函数表达式。从维护活动分类的角度考虑，设备维护成本通常包括两类：（1）出现故障后，工作人员对设备进行维护直至重新达到运营标准所花费的成本；（2）对设备进行定期事前维护工作所花费的成本。

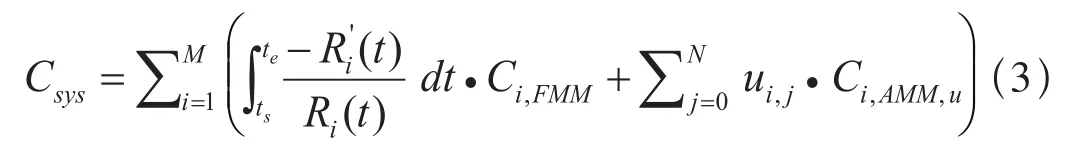
其中，Ci,FMM表示部件i进行故障后维修时，工作人员对设备修理直至其能重新投入运营环境所花费的费用（均值）；Ci,AMM,u表示部件i采用定期事前维修类型u时，工作人员对设备修理直至其能重新投入运营环境所花费的费用（均值）。N为在周期t∈（ts, te]内维修活动的次数；ui,j为部件i在第j次维修活动中采用的维修方式。

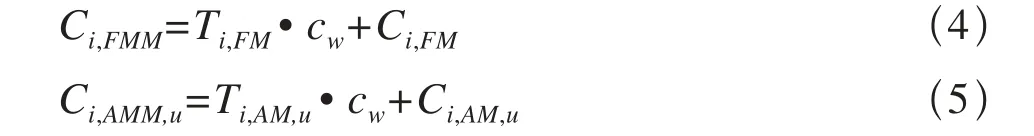
其中，Ti,FM是系统部件i进行故障后维修所需要花费的平均时间；Ti,AM,u是系统部件i以事前维修方式u所需要花费的平均时间，cw是运营维修人员或者是外聘技术支持所花费的单位时间人力成本（均值）；Ci,FM是部件i进行故障后维修时，工作人员对设备修理直至其能重新投入运营环境所花费的工料成本；Ci,AM,u是部件 i采用事前模式 u 后，从工作人员对设备维护开始直至其能重新投入运营环境所花费的工料成本。

维修类型u取值范围为[1,2,3]，其中，1表示保养,指对设备运行环境所作出的改善，例如增加润滑、去除灰尘、调节设备工作模式等；2表示修理,指维修或更换目标设备中的某些小部件，并恢复部分由于损耗而导致的设备性能衰退；3表示更换,指采用新购的设备替换原有故障的设备。

2.2 约束条件

（1）系统技术可用度

综合考虑信号系统设备在运营环境下出现故障的概率以及事前维护计划所采用的维护策略组合，技术可用度较为真实地反映了该设备在特定运营环境中的运行状态。它指代设备扣除因故障而进入维修状态所占的时间，以及因采取事前维护所占的时间，剩余的正常运转时间占周期t∈ (ts, te]的比例，表示为：

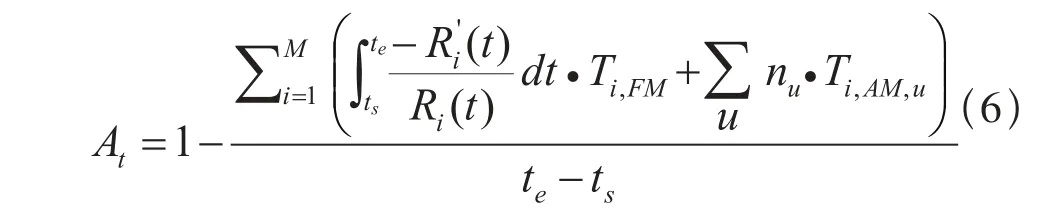
（2）系统安全性

为了保证系统的安全，系统的平均故障时间应大于维修策略中最长不进行维修工作的时间，表示为：

其中，fi(t)表示部件i的故障概率密度函数；ni,r是参考因子，通常取1.5～2；Ti,NM表示部件i本次维修策略中最长不进行维修工作的时间。

2.3 参数设置

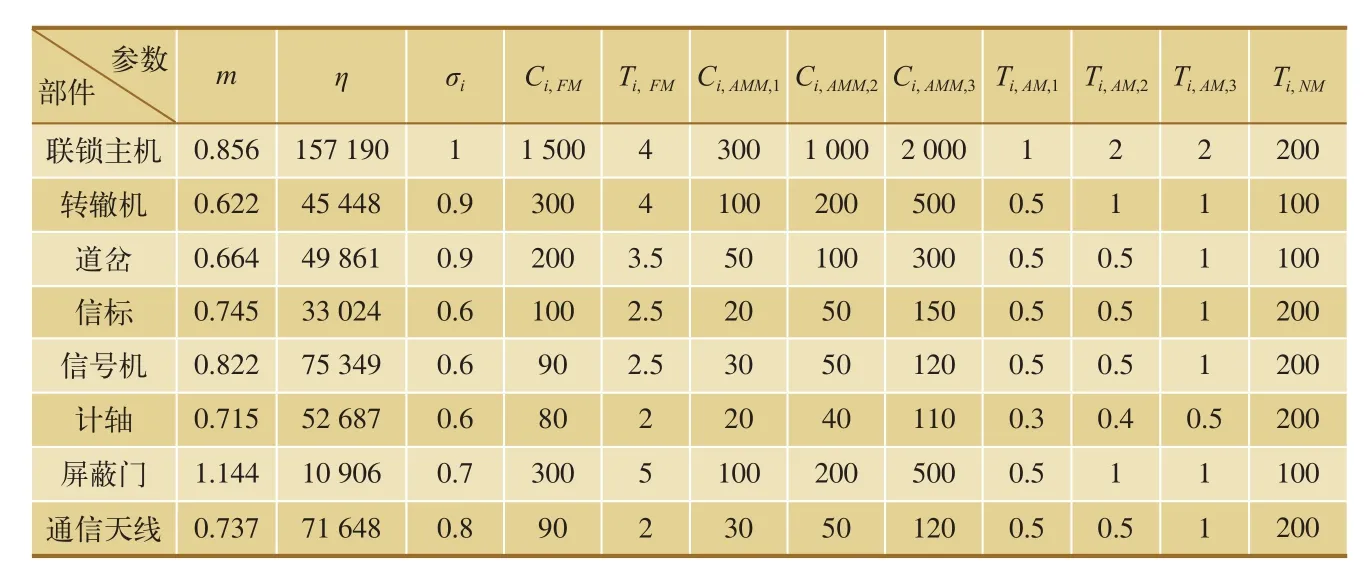
表1 信号系统可靠性及维修相关参数表

在表1中，m和η是系统中关键部件的韦布尔分布模型形状参数和尺度参数，可以简化采用二参数weibull拟合，其可靠性函数的表达式为：

其中，Ri(o)是部件i出厂可靠性（或称起始可靠性），常值为1，因此而得到关键部件的动态可靠函数Ri(t)；σi指代当该设备无法正常运行后，信号系统因此导致整体失效的概率；数值出自南宁轨道交通运营维修过程中得到的现场数据。

一般而言，事前维修都可以使目标设备的性能得到某种程度的修复，运行状态因而优于维修前。尽管如此，依然无法使得目标设备完全恢复至出厂时的状态。因此，在可靠性计算时，每次故障维修后，维修目标的设备性能状态降低一定量。

3 基于粒子群算法的目标优化计算

本研究可以看作是基于PSO算法的二维多目标优化求解。初始设定包括种群内各粒子的空间坐标x及带方向的运行速度v，求解目标共两个，即平均可靠性与维修费用，同时个体需要满足可用性及安全性约束。

应用前文构造的表达式，将系统的维修费用模型和平均可靠性模型设为优化目标，约束条件为系统的可用性，并将该约束条件数值设定为必须大于0.85。安全性约束的表达式可以变化为分散系数ni,r取值1.7。目标及约束表达式如下：

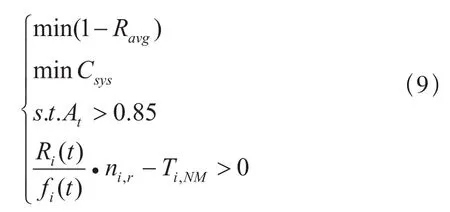
对于运算过程中出现的不满足约束条件的个体，其Pareto排序将被设置为最低。应用标准PSO方案及引入退火机制的PSO方案求解。

3.1 基本粒子群算法求解流程

利用基本粒子群算法的二维多目标优化求解的流程如图1所示：

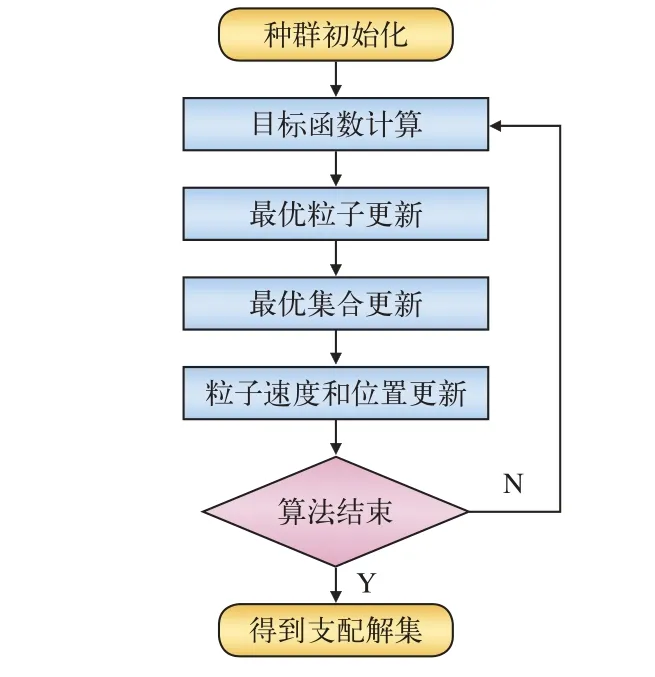
图1 二维多目标优化求解的流程图

（1）种群初始化：指系统随机生成粒子的初始位置。

（2）目标函数计算：通过目标函数及约束条件计算 Ravg和 Csys。

（3）最优粒子更新：分为个体最优和全局最优两种形式。前者会在通过运算后新形成的粒子和原粒子池中挑选Ravg和Csys最优秀的个体，如果难以比较，或者认为两个参数均为出现最理想的数值，则通过随机函数取其中的一个做为进行下阶段计算前的最优个体；后者是指从所有最优集合中通过随机函数获得的个体。

（4）最优集合更新：当某一个个体的Ravg和Csys都优于其余个体，则把该个体放入最优集合中；另一种情况，通过运算后新形成个体，其Ravg和Csys都比其余个体或者最优集合中的个体要优秀时，这个新个体需要增加到最优集合。

（5）粒子速度和位置更新：以当前最优集合中的个体所对应的速度与位置，生成空间坐标中的当前非劣解。

（6）算法结束：当迭代次数达到预报上限或最优解平均变化范围小于预设阈值时算法结束，否则返回迭代过程。

3.2 引入退火机制算法求解流程

如引入模拟退火机制，则可在主体流程中增加杂交运算与高斯变异，在调整群体时增加优化操作。算法流程修改如下：

（1）种群初始化参数：交叉概率Pc，变异概率Pm，学习因子C1和C2，温度冷却系数C，退火初始温度T；

（2）采用Tent映射产生N个粒子的种群，增加种群初始粒子的多样性；

（3）种群中所有粒子都采用以下公式进行调整与更新：

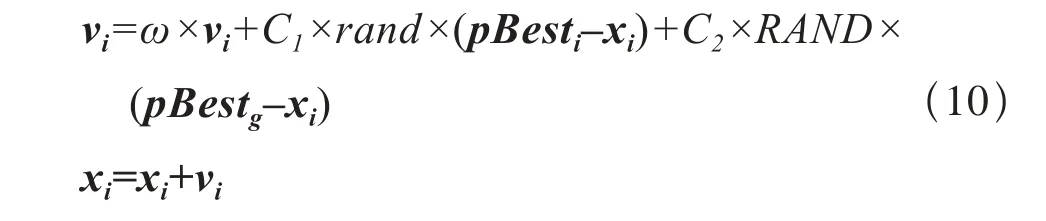
其中，rand与RAND是（0,1）区间上的随机取值，pBesti是个体最优粒子位置，pBestg是全局最优粒子位置。

（4）对步骤（3）中得到的新种群以概率Pc选取粒子组成子种群，并执行以下操作，使得子种群形成下一代的新种群：从子种群中随机选取两个个体xj，xk，按以下公式执行交叉操作，产生两个新的粒子个体 xj'，xk'。

其中，p是(0,1)区间上的随机取值。代入适应值表达式计算，如果min{1,exp[–f(xj')–f(xj)]/T}＞random，将xj'作为新粒子个体，同理处置xk'。random为(0,1)区间上的随机取值。

（5）对步骤（4）中得到的新种群以Pm选取粒子组成子种群，并执行以下操作，使得子种群形成下一代的新种群：从子种群当中选择个体xj，按式（12）执行高斯变异操作，产生一个新的粒子个体xj'。

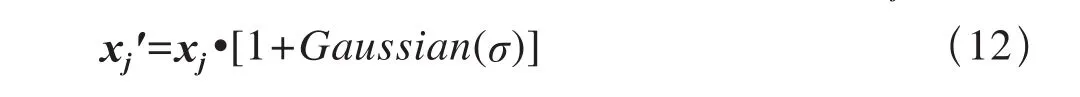
代入适应值表达式计算，如果min{1,exp[–f(xj')–f(xj)]/T}＞random，将xj'作为新粒子个体。

（6）若当前最优解满足既定的收敛条件，则进化完成；如不满足，执行退火操作：Tk+1=CTk，其中，C是（0,1）区间上的随机取值，并转至步骤（3）。

3.3 算法优化结果比较

将退火机制中的交叉概率设为Pc=0.5，变异概率Pm=0.05，温度冷却系数C=0.8，退火初始温度T=100 000，采用Matlab进行模拟优化计算。算法结束条件设定为500代或是最优解平均变化范围小于0.000 5。得到标准粒子群算法与引入退火机制的粒子群算法的优化结果比较,如图2所示。其中，横坐标为系统的平均不可靠度（即：1–Ravg），纵坐标为系统的维修费用（元）。

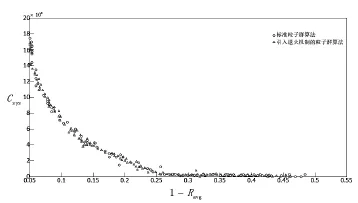
图2 两种算法优化计算结果比较图

由图2可知，引入退火机制的算法得到的结果与标准粒子群算法得到的结果进行比较，前者分布更为均匀，收敛性能更好，Pareto最优解集数量更多，更接近真实前端，决策者可以选择的范围也更广泛。

3.4 算法进化过程

图3为每间隔一定的代数，获取的Pareto前端变化图。

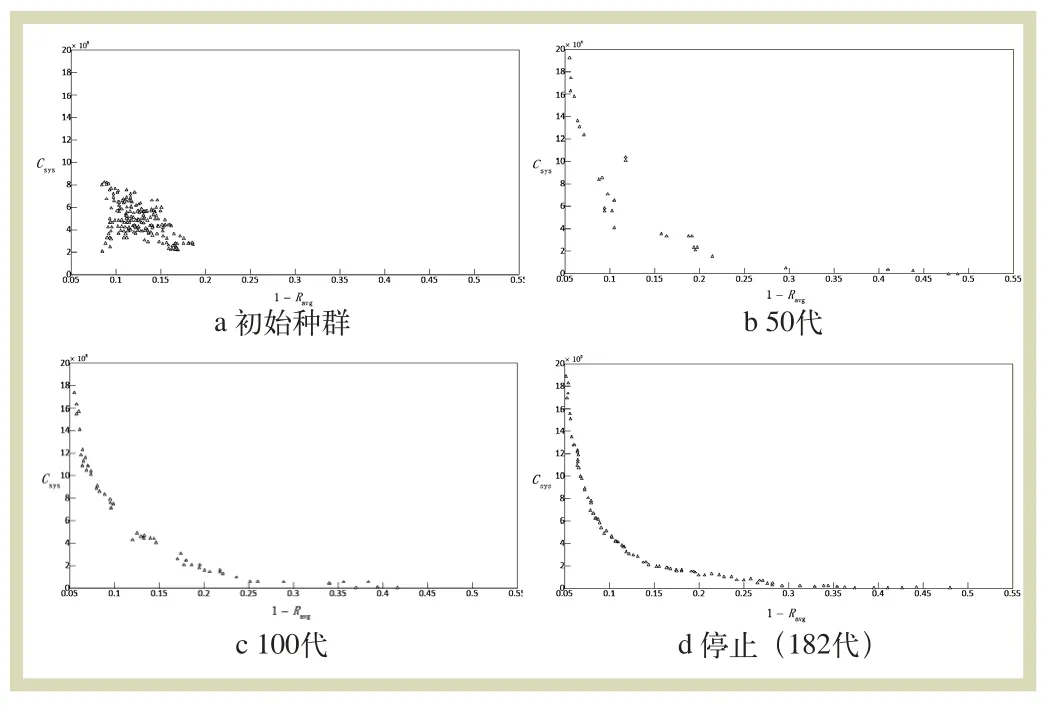
图3 优化计算过程比较图

通过观察可知，初始种群的分布较为广泛，当完成50次迭代后，最优解集中的解的数量较少，而且并无轨迹可循。在完成100次进化后，初步呈现规律，并逐渐向原点移动，数据点的分布也趋向均匀，最终接近一条完整的弧线。随着解集中解数量的不断增加，最后满足收敛条件（本次研究182代时最优解平向变化范围小于0.000 5），完成计算，如图3d所示。越靠近原点（可靠度越高），所需要额外支出的费用更多，在一定的维修次数下，通过维修工作来提升信号系统可靠性的前提就是维修费用的上涨。

4 优化结果和维修策略制定

决策人员可以调整求解问题对应的约束条件，再次求解以获取不同的解集进行对比选择。

例如，作为约束条件之一的系统可用度，分别采用0.85和0.95时获取的最优个体集合是不一样的，如图4所示。决策人员可以根据运营的实际情况采用对应的维修策略以达到既定的目标与效果。

由图4可知，可靠度与维修费用的数值基本上是同时增加的。采用不同的可用度数值时，在要求的可靠度不变的前提下，可用度的预设值越大，维修成本支出也就越大。两个最优解集的规律是相似的，但可用度约束条件低的最优解集更接近前端。

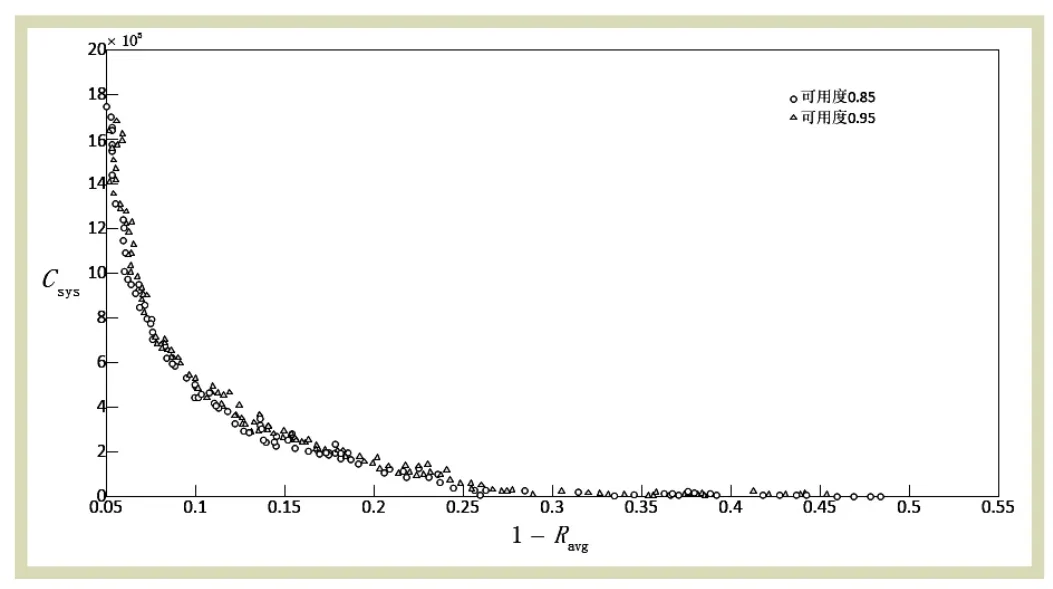
图4 不同技术可用度优化计算结果比较图

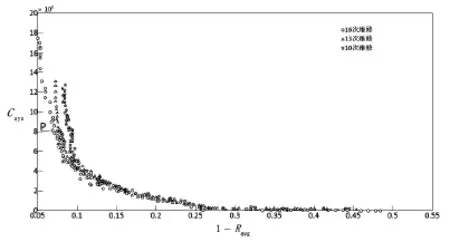
图5 不同维修次数优化计算结果比较图

如果修改维修工作的次数，对优化计算的结果影响也是明显的，也可以给决策人员提供更多的选择。图5为采用10次、13次、16次维修时，信号系统以可靠度与维修费用为适应度的最优解集。

提高系统的可靠性而相应增加维修费用的趋势并没有变化，但是在同样时间间隔中增加维修工作的数量，需求同样可靠度的条件下，会降低维修费用的支出。最终如何选定，取决于决策者对不同因素的选择。在图中选取一点P，对应16次维修，费用为82.759万元，信号系统平均可靠度为93.15%，对应可用度为95.83%。表2列出P点所采用的定期事前维修策略。

整个信号系统中，联锁主机与信号机的可靠度是最高的，一般而言，做好周期性的维护即可满足要求。屏蔽门的故障率较高，需要加强其维修及更换的次数，保证整个系统的平均可靠度。

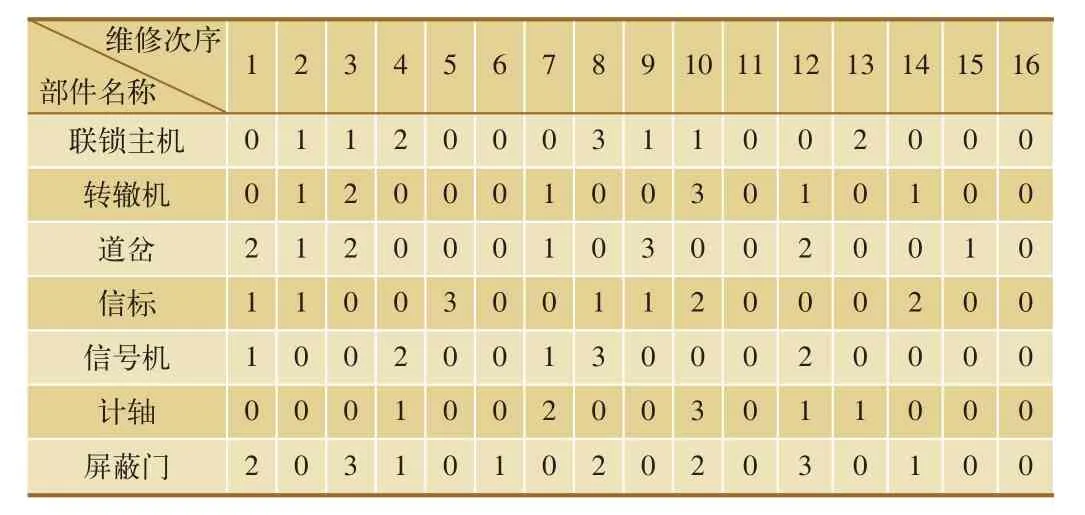
表2 信号系统关键部件维修策略

5 结束语

本文研究了轨道交通信号系统维修策略的优化方案，分析了维修策略优化的关键内容。通过建立数学模型，对信号系统设备采用的维修策略进行研究，讨论不同维修方式的组合对于整个系统可靠性、可用性、安全性及维修成本支出的影响。研究了各类多目标优化算法，分析相关算法理论，并确定采用多目标粒子群算法作为本项目维修策略优化的数学工具。以信号系统的平均可靠度与维修费用共同作为粒子群算法的二维优化目标，并将信号系统的可用性及安全性设定为算法的约束条件，建立相应的多目标优化模型；应用标准粒子群算法及引入退火机制的粒子群算法进行寻优计算，最终获取维修策略的全局最优解集。

对于控制中心、车站、区间及车载信号系统设备的维护应在非运营时间内进行。如果某设备是冗余配置（如双机热备）的话，在运营时间内对其中一套设备采取维修工作，另一套设备照常运作，通常并不会对整个系统的有效运行造成不良的影响。

如果设备只有单独一套，例如信号机、计轴、无线传输天线等，定期的事前维护相对就显得重要了。运营人员在制订维修策略时，应对这类设备的可靠性统筹把握，按照标准、规范及公司的规章制度对其进行维护工作。

[1] 陈 蕾. 城市轨道交通引入RAMS管理的必要性[J]. 城市轨道交通研究, 2007, 10（5）：4-7.

[2] 乌鲁木齐铁路局. 铁路安全风险管理[M]. 中国铁道出版社,2013.

[3] 陶 涛, 龙 静, 龚 玲. 可靠性管理在城市轨道交通车辆全寿命周期内的应用[J]. 城市轨道交通研究, 2014, 17（12）：4-7.

[4] Wu D D, Zhang Y, Wu D, et al. Fuzzy multi-objective programming for supplier selection and risk modeling: A possibility approach[J]. European Journal of Operational Research, 2010, 200(3):774-787.

[5] Baky I A. Fuzzy goal programming algorithm for solving decentralized bi-level multi-objective programming problems[J].Fuzzy Sets & Systems, 2009, 160(18):2701-2713.

[6] Tanino T, Tanaka T, Inuiguchi M. Multi-Objective Programming and Goal Programming[M]. Springer Berlin Heidelberg, 2009.

[7] Nakayama H. Interactive Multi-Objective Programming and its Applications[M]// Methodology, Implementation and Applications of Decision Support Systems. Springer Vienna,1991:175-197.

[8] Zhou R, Yan Y, Qiu Z. A Multi-Objective Programming Model of Railway Network Planning[C]//American Society of Civil Engineers, 2009: 3338-3343.

[9] Zhang Q, Li H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[M]. IEEE Press, 2007.

[10] Veldhuizen D A V, Lamont G B. On measuring multiobjective evolutionary algorithm performance[C]// Evolutionary Computation, 2000. Proceedings of the 2000 Congress on.IEEE, 2000:204-211 vol.1.

[11] Van D A, Gary V, Lamont B. Multiobjective Evolutionary Algorithm Research: A History and Analysis[J]. Evolutionary Computation, 1998, 8(2):125 - 147.

[12] Zhang J, Zhou A, Zhang G. A Multiobjective Evolutionary Algorithm Based on Decomposition and Reselections[C]// Bio-Inspired Computing - Theories and Applications. Springer Berlin Heidelberg, 2015:631-642.

[13] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by Simulated Annealing [J]. Science, 1983, 220(4598):671.