基于硬件在环仿真的系统模型辨识平台设计

邹宇鹏, 吴宝贵, 崔学政, 孙少华

(中国石油大学(华东) 机电工程学院，山东 青岛 266580)

0 引 言

工程实践中，伺服控制系统设计多以频域设计为主，即采用经典控制理论[1-3]。基于频率特性的控制系统设计的前提是得到精确的系统数学模型。但考虑到系统中各项参数摄动、未建模动态特性以及非线性的影响，理论模型与实际系统出入较大[4-7]。

本文以柔索驱动系统为研究对象，建立了系统数学模型；为了验证理论模型的准确性，搭建基于dSPACE的硬件在环仿真平台，采集输入、输出数据，利用MATLAB-ident工具箱对实际系统模型进行辨识，为系统特性的分析和控制系统的设计奠定基础。

1 系统模型

柔索驱动系统的组成如图1所示。系统采用直流力矩电动机作为驱动元件，提供负载力；通过柔索将负载力传递到承载对象上[8]。

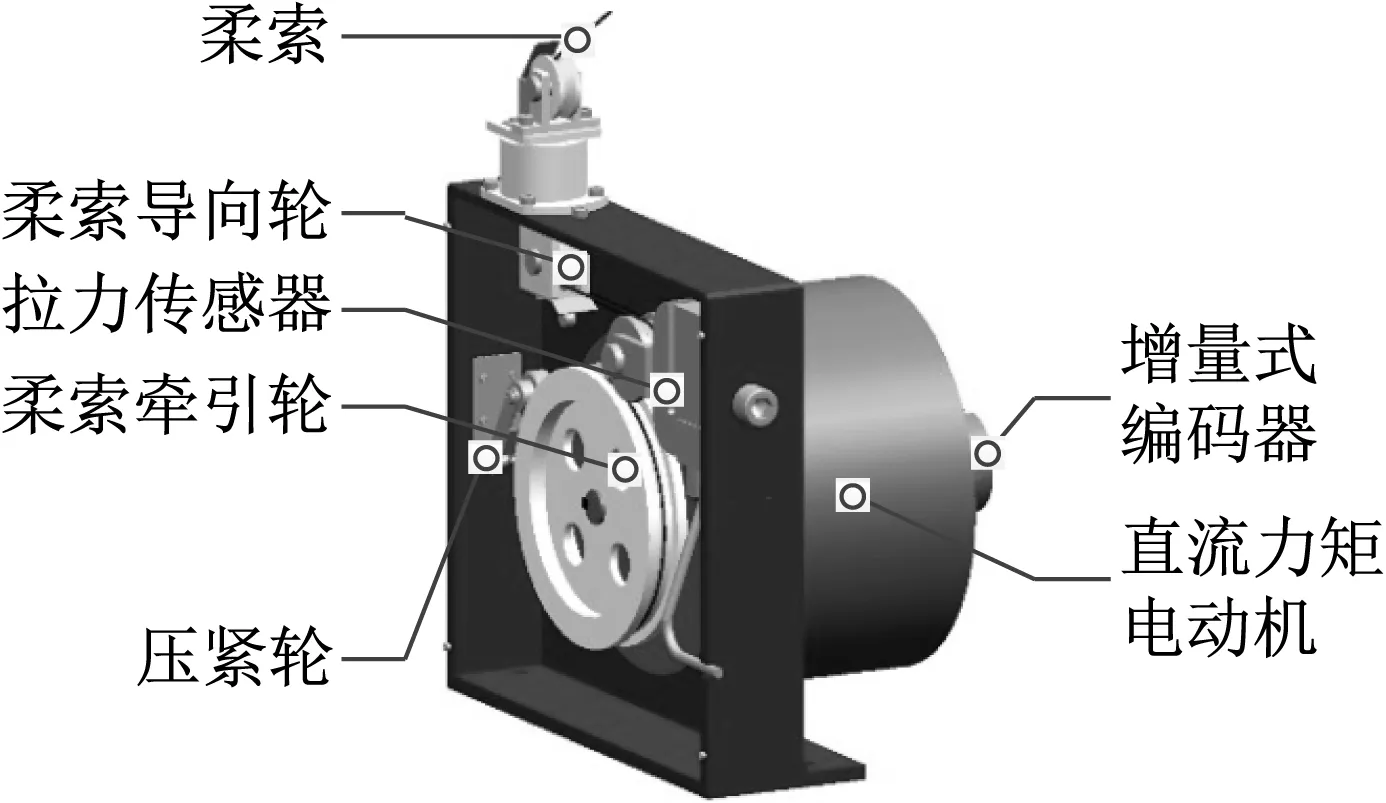
图1 柔索驱动系统

柔索驱动系统机理模型如图2所示。

图2 柔索驱动系统机理模型

图2中,u是电动机电枢电压;L是电感;R是电动机电枢回路的电阻;e是反电动势;i是电流;Ce是反电动势常数;Cm是力矩常数;Tm是驱动力矩;T1是外负载力矩;Jm是转动惯量;Bm是传动机构等效黏滞摩擦系数;θm是牵引轮转角;r是柔索牵引轮半径;M是柔索质量;K是柔索刚度系数;B是柔索阻尼系数。

对于柔索所简化成的单自由度“质量-弹簧-阻尼”线性模型，柔索末端固定，其在外力作用下的强迫振动的理论模型如图3所示。

图3 柔索强迫振动模型

柔索强迫振动传递函数如下式所示:

(1)

由图2可得到，在考虑承载对象运动影响，柔索驱动系统数学模型为

F(s)=M1(s)U(s)-M2(s)V0(s)

(2)

式中,V0(s)=sY0(s)是柔索末端的运动速度。

M1(s)是从输入电压U(s)到输出F(s)的模型，是指令前向进入的通道，称为前向通道传递函数；M2(s)是输入V0(s)到输出力F(s)的模型，是多余力产生的通道或扰动的通道，称为多余力传递函数[9,10]。

前向通道传递函数为

M1(s)=Cmr(Ms2+Bs+K)/[JeLs3+(BeL+JeR)s2+

(BeR+CmCe+KLr2)s+KRr2]

(3)

多余力传递函数为

M2(s)=(Bs+K)[JmLs2+(BmL+JmR)s+

(BmR+CmCe)]/[JeLs3+(BeL+JeR)s2+

(BeR+CmCe+KLr2)s+KRr2]

(4)

式中,Je=Mr2+Jm和Be=Br2+Bm分别是系统的等效转动惯量和等效黏滞摩擦系数。

2 辨识实验平台

辨识系统原理框图如图4所示。

图4 辨识系统原理框图

模型辨识基本原理是：上位机根据输入信号(柔索张力f、电压u或者速度v)发送控制命令；经电动机驱动器对控制指令进行功率放大，以电压形式输入到柔索驱动系统；柔索驱动系统输出信号(柔索的伸长量x或者柔索张力f)经调理电路输入到上位机；利用dSPACE-controldesk软件记录柔索驱动系统的输入输出数据[11-13]；调用MATLAB-ident工具箱，对实验数据进行处理，完成柔索驱动系统的模型辨识[14]。

3 系统模型辨识

在图4所示的实验平台的基础上，分别对传递函数Gcable(s)、M1(s)和M2(s)进行模型实验验证。实验时，期望力f、期望电压u以及期望柔索运动速度v均以周期方波信号的形式输入。由于柔索受力的单向性(只能拉不能压)，因此在实验时先给系统施加一个正的基准信号，保证柔索处于拉伸状态。然后在此基础上施加方波信号。考虑到系统的时变和干扰，进行多组实验，向系统中输入频率0.5 Hz、幅值不同的方波信号。

3.1 柔索传递函数Gcable(s)模型实验验证

根据式(1)，从输入力F到柔索长度变化量x的对象模型即为Gcable(s)。实验步骤如下：

(1) 将柔索末端固定，先向柔索驱动系统输入一个基准拉力F0，使柔索处于张紧状态，然后向系统输入一定幅值的方波力信号，利用ControlDesk实时测试显示软件实时采集记录柔索实际张力f和实际柔索长度变化量x。

(2) 利用MATLAB的ident图形辨识工具箱对实验数据进行处理，完成系统的辨识。以输入力为100±40 N为例，模型辨识过程如图5所示[15]。

①数据预处理。使用MATLAB采集到的实时数据，并分别把输入和输出数据传递给变量u和y，打开ident图形辨识工具箱(如图5(a)所示，命令ident)，在import data下拉菜单中选择Time domain data选项，将Workspace中的变量u和y导入到工具箱中，如图5(b)所示。

②模型类型选择和参数估计。在Estimate下拉菜单中选择Linear parametric models选项，确定参数模型的结构形式，(如图5(c)所示)。

选用输出误差(OE)模型来估计柔索模型[16]。输出误差(OE)模型为

(5)

图5(c)中，Orders选项用来确定传递函数模型的阶次。根据式(1)，令nb=1、nf=2、nk=2，表示模型中分子多项式为1项，分母的最高阶次是2，分子比分母低2个阶次。完成模型选型后，工具箱会根据确定的结构形式得到系统模型oe122。

③模型验证。完成参数辨识后，在ident界面右侧生成一个oe122的数据图表，即ident估计得到的系统模型。辨识模型的输出如图5(d)所示，与实际系统的相似程度达到95.16%。将辨识得到的模型传递到MATLAB的Workspace工作空间，建立模型的传递函数(命令tf)，利用零极点匹配的方法，将离散的传递函数连续化(命令d2c)，辨识得到的柔索模型传递函数为

(6)

将模型中各参数的标称值代入式(1)中，理论建模得到的柔索传递函数为

(7)

(3) 重复①②两步，进行多组实验。

(4) 将各次实验所辨识得到的系统传递函数Gcablei(s)(i为实验次数)以及标称模型Gcable0(s)的频率响应曲线绘制到一起，如图6所示。

从图6中可以看出，柔索的实际频率响应曲线围绕着理论模型上下浮动，浮动的大小反映了在当前实验条件下的柔索模型的不确定性，如图中虚线范围所示；此外，柔索模型不确定性范围在低频段很小。由于柔索传递函数Gcable(s)是可信的，基于硬件在环仿真的系统模型辨识平台是有效的。

(a) ident工作界面(b) 数据导入工作界面(c) 模型参数工作界面(d) 模型输出界面(e) 前向通道传递函数的理论模型及辨识模型伯德图

图5 基于ident图形辨识工具箱的模型辨识

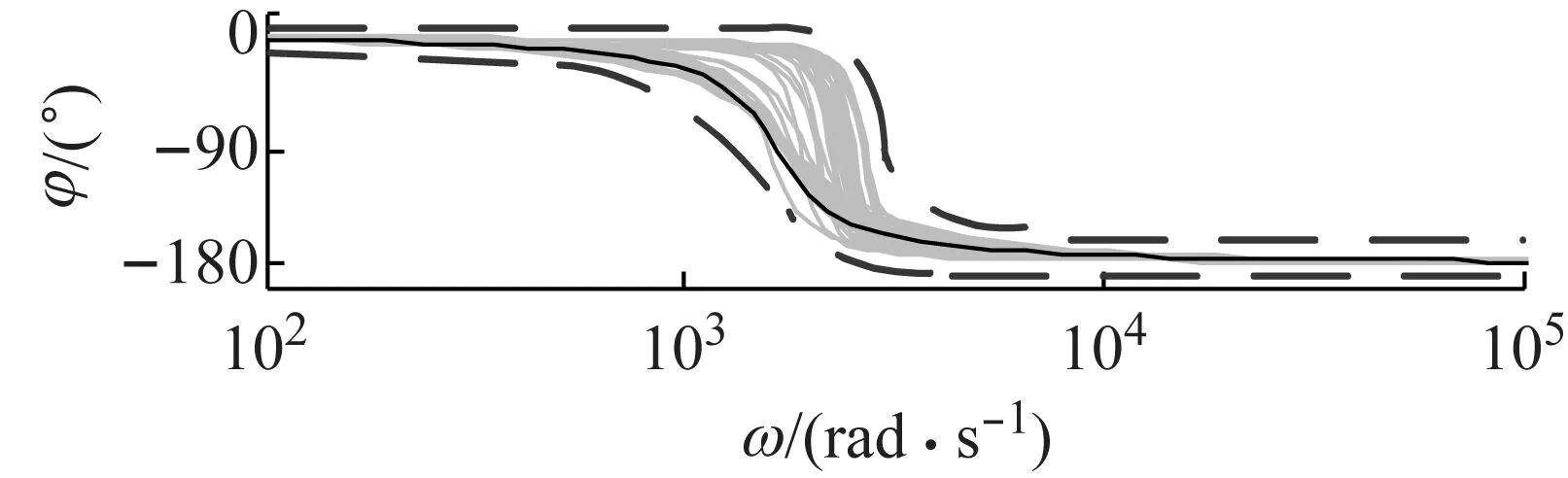
图6 柔索传递函数辨识结果

3.2 前向通道传递函数M1(s)模型实验验证

根据式(2)，当速度输入V0(s)为0，从电压U(s)到输出F(s)的对象模型即为M1(s)。对于实际系统，相当于将柔索末端固定，根据输入到系统的方波电压信号U(s)和输出力信号F(s)来构造实际系统的前向通道传递函数模型M1(s)。

与柔索模型Gcable(s)的辨识过程类似，M1(s)模型辨识结果如图7所示。

图7 前向通道传递函数的模型辨识结果

由图7可见，系统前向通道的实际频率响应曲线围绕着理论模型上下浮动，且在理论模型频率特性曲线两侧均匀分布。在低频段，模型不确定范围较小，根据式(3)，前向通道的低频增益K=Cm/(Rr)，根据力矩常数Cm和电阻R的取值可确定辨识结果是有效的。辨识模型在1 000～2 000 rad/s左右的频率范围频率特性曲线明显发生转折。根据式(3)，前向通道频率特性的变化受分子二阶微分环节的影响，该转折频率与柔索模型的转折频率相一致。对比图6和图7可以看出，二者的转折频率大致是吻合的。实验结果进一步确定辨识方法是有效的。

3.3 多余力传递函数M2(s)模型实验验证

根据式(2)，当输入U(s)为0，从输入V0(s)到输出力F(s)对象模型即为M2(s)。对于实际系统，相当于将电动机驱动器断电，利用另一个速度伺服电动机拖动柔索驱动系统，根据实际输入到柔索驱动系统的速度信号v0和输出力信号F来构造系统多余力传递函数模型M2(s)。辨识结果如图8所示。

从图8中看出，多余力的实际频率响应曲线都集中在图中虚线范围内，虚线范围的大小反映了当前实验条件下模型的不确定性。根据式(4)，多余力传递函数在低频段的幅值K=(CmR+CmCe)/(Rr2)，根据力矩常数Cm、反电动势常数Ce和电阻R的取值可确定辨识结果是有效的。在速度伺服电动机拖动柔索驱动单元的过程中，速度由快到慢变化的瞬间柔索处于相对松弛状态，柔索刚度降低，考虑到柔索刚度K等非线性因素的影响，可确定基于dSPACE的硬件在环仿真的系统模型辨识方法对于多余力传递函数M2(s)也是有效的。

图8 多余力通道模型辨识结果

4 结 语

本文以柔索驱动单元为研究对象，建立了在考虑承载对象运动影响的情况下的完整的柔索驱动被动式力伺服系统的数学模型；进一步搭建基于dSPACE的硬件在环仿真系统；再利用MATLAB-ident工具箱在离线状态下对柔索模型，前向通道模型和多余力模型进行模型辨识。结果表明，实际系统模型与理论模型的差异不大，验证了基于dSPACE硬件在环仿真的系统模型辨识方法的有效性。本文的研究工作为控制系统特性分析以及控制策略设计奠定了理论和实验基础。此外，实验采用的仿真平台容易搭建，辨识软件开放简单，便于实验教学和科学研究，该系统的设计方法具有一定的推广价值。

参考文献(References)：

[1] 郑 雯. 基于频率域的伺服系统建模、分析与控制[D].南京:东南大学,2016.

[2] 陈晓娟. 自动控制系统频域分析的GUI仿真设计[J]. 电子设计工程, 2014, 22(22): 39-41.

[3] 幸 权,唐 猛,张 兵. 电机伺服控制PDF策略频域设计方法优化[J]. 测控技术,2014,33(11):85-88.

[4] 刘 龙,姚建勇,胡 健,等. 基于干扰观测器的电液位置伺服系统跟踪控制[J]. 兵工学报,2015,36(11):2053-2061.

[5] 李江平. 模型及负载不确定情形下机械臂自适应运动控制[D].北京:北京理工大学,2016.

[6] 邵俊鹏, 王仲文, 李建英, 等. 电液位置伺服系统模型辨识与非线性控制[J]. 机械科学与技术, 2010, 29(4): 488-492.

[7] 沈 伟, 兰 山. 伺服系统频率特性测试方法研究[J]. 实验技术与管理, 2011, 28(11): 268-271.

[8] 邹宇鹏, 张立勋, 李来禄. 多模式柔索驱动航天员训练机器人力控制[J]. 宇航学报, 2015, 36(5): 566-573.

[9] 李成功, 靳红涛, 焦宗夏. 电动负载模拟器多余力矩产生机理及抑制[J]. 北京航空航天大学学报, 2006, 32(2): 204-208.

[10] WANG Xingjian, WANG Shaoping, ZHAO Pan. Adaptive fuzzy torque control of passive torque servo systems based on small gain theorem and input-to-state stability[J]. Chinese Journal of Aeronautics, 2012, 25(6): 906-916.

[11] 谢海斌,龙志强,史美萍. 面向dSPACE的实验教学探索与实践[J]. 实验室研究与探索,2012,31(7):158-164.

[12] 张 奇. 基于V模式的dSPACE电机控制器开发[J]. 实验室研究与探索,2014,33(11):141-144.

[13] 许小庆, 李凤兰. 利用DSpace实现电液伺服系统研究的实验方法[J]. 实验技术与管理, 2012, 29(4): 90-92.

[14] 刘兆田, 李敬敬, 何 旭, 等. Matlab系统辨识工具箱在煤泥浮选过程辨识建模中的应用[J]. 选煤技术, 2014(6): 77-80.

[15] 张立勋. 机电系统建模与仿真[M]. 哈尔滨:哈尔滨工业大学出版社, 2010.

[16] 丁 锋. 输出误差系统的多新息辨识方法[J]. 南京信息工程大学学报(自然科学版), 2015, 7(6): 481-503.